光电导引的四轮移动机器人设计

(南京理工大学 自动化学院，南京 210094)

0 引言

四轮移动机器人的研究具有很强的实际意义。它去除了主观性很强的人为控制，用控制系统代替，提高系统的效率和运输的安全性[1]。文献[2]根据检测到黑线的光电管的位置判别舵机的偏转角度结合PI控制器给出相应的速度控制信号；文献[3]通过增量式PID算法实现智能车速度控制，根据运动叠加原理通过电机转速的调节实现行驶和转向功能；文献[4]通过对速度进行PID控制，通过两轮差速实现小车方向控制；文献[5]利用单边寻迹法即控制小车只沿一条黑线行驶。本文设计的光电导引的四轮移动机器人，利用模糊控制实现前轮转向，基于解析式控制器的智能自适应PID实现后轮驱动，基于二值化灰度值的双向跳变沿检测法实现路径识别与提取，中心线寻迹法实现赛道判别与路径寻迹。机器人能按赛道要求实现快速平移和转向，同时验证了硬件系统的可行性和控制算法的有效性。

1 系统总体设计

1.1 运行环境及控制要求

机器人运动路面由直道、不同曲率半径的圆弧、拐弯、十字交叉路口和路障组合而成，赛道宽度不小于45 cm，赛道与赛道中心线之间的距离不小于60 cm。赛道信息的检测通过线阵CCD完成。使机器人在赛道自主稳定、快速地运行具体需要实现：

1)跑道检测，完成路径规划；

2)电机转速的检测与控制；

3)前轮转向的控制。

1.2 器件选型及布局

设计选用的MCU核心芯片是飞思卡尔公司的单片机MC9S12XS128。E6A2-CW3C光电编码器作为测速元件；比赛规定需要采用SD-5型号舵机，其工作频率最高达300 Hz；选择RS540的直流电机作为系统执行机构；采用蓝宙公司的线性CCD(其型号为TSL1401)作为光电传感器，其分辨率为128×1；无线通信采用蓝牙设备来实现。

为使机器人转向轻便，须使车模重心尽量落在左右中心线上，前后位置则靠近动力轮；舵机S-D5极易撞坏，因此在舵机前方应该加装防撞海绵；将舵机前移，使CCD直接固定于底盘上。

1.3 控制系统组成

根据控制任务要求，将光电导引的四轮移动机器人控制系统分解为前轮转向和后轮驱动两个子模块。单片机通过线阵CCD采集到的赛道信息结合制定的赛道判别方法判断当前的赛道情况，调整PWM信号的占空比。将占空比输入到前后轮模块分别调节角度和速度，使机器人沿赛道运行。数据通过蓝牙传输给上位机。

2 控制算法设计

优质的控制算法保持机器人平稳快速运行的关键。光电导引的四轮移动机器人总体控制设计如图1所示。

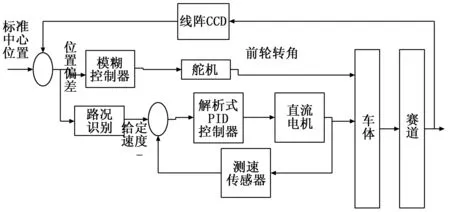
图1 控制系统设计

2.1 前轮转向系统建模及算法设计

为建立四轮移动机器人前轮转向数学模型，假设轮胎不会打滑，不考虑轮胎由于受到重力而产生的形变并且不考虑左右两侧轮胎因为受力不均匀而发生的形变。

舵机是一个闭环系统，接收到单片机产生的PWM控制信号后产生转角。本次大赛使用的舵机型号是S-D5，响应速度快。其运动到设定角θ的时间t和转角呈线性关系：

t=Kθ

(1)

多次测试证明，舵机转角与PWM信号的占空比也基本呈线性关系。则舵机响应时间与PWM信号的占空比可以表示为：

t=K′ρ

(2)

对于前轮转向控制，快速性很重要，特别是在弯道，舵机快速响应机器人才能不冲出赛道。即面对不同情况，控制效果不同。此外，在实际的控制中，控制量是线阵CCD采集回来的赛道信息，且舵机转向力学建模较复杂，精确的数学模型很难建立。模糊控制灵活性强，正适用于此类复杂模型。

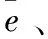
表1 模糊控制规规则表

2.2 后轮驱动系统建模及算法设计

整个后轮驱动模块包含：PWM脉冲产生、光电隔离、驱动电路、电机和测速编码器。参考文献[6]用用一阶惯性环节近似替代PWM产生并与驱动电路整合，其传递函数PWMs(s)为：

(3)

将扰动输入量IdL作用点提前的额定励磁条件下直流电机的结构图见图2。

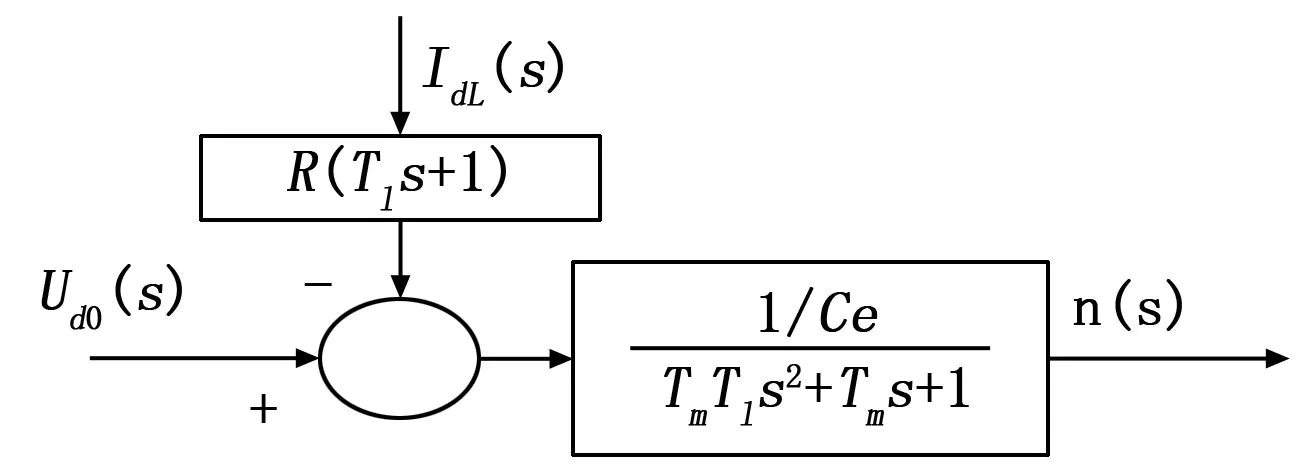
图2 直流电机结构图

测速环节表达式为：

(4)

考虑到Tl非常小，将电机可以简化成一阶模型(1/Ce)/Tms+1。结合之前各模块模型后得到如图3的转速控制模型，可以看出后轮驱动模型是一个二阶模型。

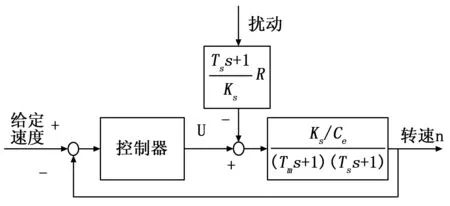
图3 后轮驱动简化模型

电机转速控制要求快速性高，超调小，稳定性强。理想情况下，机器人在转弯和过十字时减速，在直道或者小S弯道上加速。事实上，机器人的位置变化率将很直接的影响速度值，所以通过位置变化率来规划机器人的速度。

当机器人进入弯道，其位置变化率不断在变大，而离开弯道时，位置变化率不断减小。通过机器人在不同赛道上的区别设置不同的速度。对机器人的偏差连续采样多次，计算变化率，对其绝对值累加并分档，累加值小的，说明在直道上，稍大一点的，说明在小S弯上，而比较大的值在大S弯上。结合赛道测试结果，给不同的路况设置不同的给定速度。

考虑到系统复杂，为了得到更好的电机控制效果，本文采用基于解析式控制器的智能自适应PID控制算法，原理如图4所示。

图4 智能自适应PID原理图

解析式控制器的输出与误差e、变化ec以及Σe有关，u=αe+(1-α)ec且α∈(0,1)。通过智能因子α来调节控制量的大小，为使误差e、变化ec尽快靠近零，当e较大时，给其大的控制量α，减小误差；当ec较大时，为使其减小则设定较大的1—α，此时α给一个小的控制量，令β=1—α，则:

u=kp×α×e+kd×β×ec

(5)

经过多次实验，参考S函数，用式(6)计算智能调节因子，即：

(6)

确定kp=106不变，调节kd。kd是微分系数，其值较小时，系统的响应速度快，超调量大；其值较大时，系统的响应慢，超调小。起初更追求响应速度，因此给微分较小的控制量；当误差的变化较大接近稳态时，给定较大kd值。类似α和β，kd与e和ec相关。令

(7)

(8)

2.3 路径识别算法设计

线性CCD的分辨率为128*1。白色的灰度值高，黑色的灰度值低，场地背景的灰度值偏低，可以得到像素灰度值曲线。若光线均匀并且线性CCD位于赛道正中，对应的像素灰度值曲线如图5所示。

图5 无反光时 图6 赛道边沿反光时

由图5可知，找到像素灰度值曲线的最大上升和下降沿，便相当于找到了赛道左右边线。传统处理赛道图像的方法为边沿检测算法，主要是单向跳变沿检测(从像素灰度值曲线的一侧逐点寻找最大上升或下降沿)。但是在比赛现场由于光线斜射、分布不均等影响，赛道边沿发生反光，使得原本部分深色的赛道背景灰度值变大，线性CCD位于赛道中间时，对应灰度值曲线如图6。赛道边沿反光造成赛道图像发生畸变，若采用传统的边沿检测算法，受反光畸变突起的影响，难于准确检测到赛道左右边沿，为此提出了双向跳变沿检测法。

双向跳变沿检测法是从线性CCD中心像素点向两边寻找最大跳变沿从而辨识到赛道左右边沿，可以避开由于赛道边沿反光产生的图像畸变。该法的一个重点是找到线性CCD中心像素点，随着机器人在赛道上运动，线性CCD也会相对赛道正中发生相对位移，但通过方向控制，机器人整体上是沿着赛道正中运动的，所以在程序运行时储存每一次的赛道正中像素值(赛道左右边沿像素均值)作为下一次的线性CCD中心像素点。此外，为了减小算法复杂度，简化操作，对采集到的赛道像素灰度值作二值化处理。之前在判断采集是否有效时都引入了有效阈值，该阈值是要通过现场查看线性CCD采集到的赛道图像对比图像中的各个跳变沿估算，操作复杂，阈值的准确度也亟待商榷。赛道像素灰度值二值化采用动态阈值，可以随着光线的变化自动调整阈值大小，这样受光线影响小，操作简单。该算法先计算动态阈值，然后将赛道图像二值化，作出灰度值折线，接着从线性CCD中心像素点向两边寻找最靠近的下降沿，从而得到赛道左右边线。动态阈值的计算可以采用大津算法，也可以采用简单的最大最小像素灰度值的平均值。。二值化后为了滤除噪声增加滤波处理，采用膨胀腐蚀算法。具体描述如下。

Step1：寻找像素点最大最小灰度值，计算动态阈值；

Step2：根据动态阈值对灰度值进行软件二值化，当前像素点i灰度值x(i)，若大于动态阈值，x(i)=1否则x(i)=0；

Step3：腐蚀膨胀滤波，即若x(i-1)=x(i+1)≠x(i)时，

令x(i-1)=x(i+1)=x(i)；

Step4：从线性CCD中心像素点分别向左、向右遍历，找到第一个灰度值等于0的像素点，这两点对应赛道左、右边沿。

实验证明，基于二值化灰度值的双向跳变沿检测法能有效地抑制赛道边沿反光的干扰，赛道图像处理效率高。

2.4 赛道判别算法设计

直道、小弯道和一侧路障：定义基准中心点为上一次采集到的正中像素值(赛道左右边沿像素均值)。计算出当前中点(mid)与基准中心点(MID)的距离，若其小于设定值，则视为直道，理想情况和实际采集上位机显示如图7～8所示。

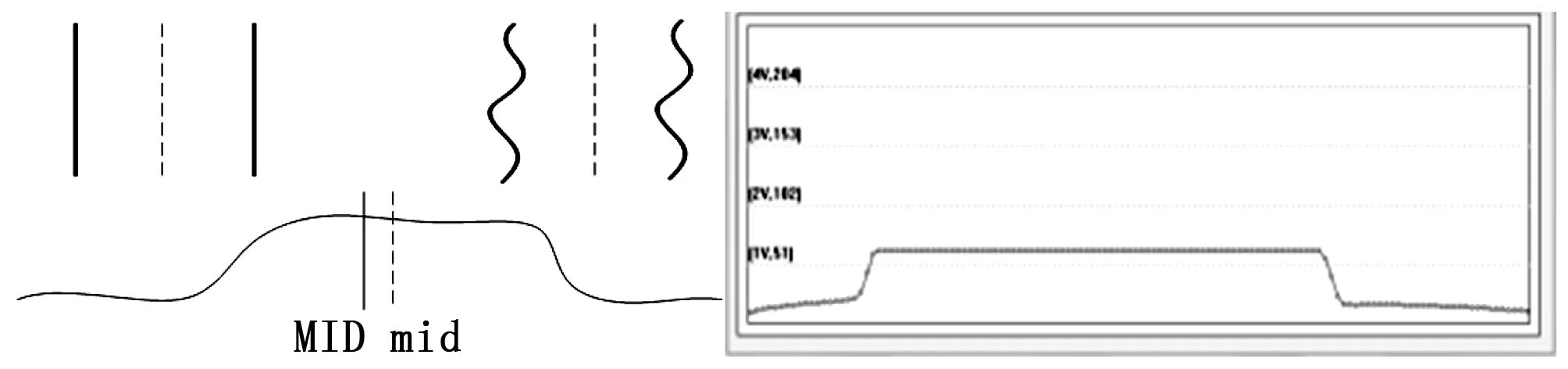
图7 直道和小弯道

图8 一侧路障

考虑到线阵CCD的前瞻性，通过一侧路障时需减速。

转弯：当前中心点(mid)与基准中心点(MID)的距离大于设定值时候，认为是转弯，理想情况和实际采集上位机显示如图9～10所示。

图9 右转弯

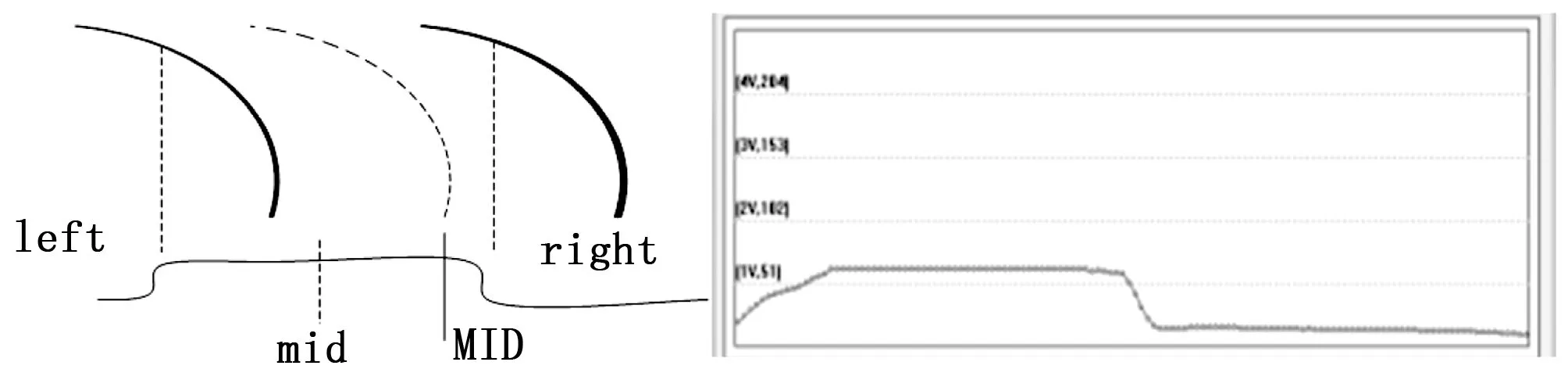
图10 左转弯

图7～10采用双向跳变沿检测法。获得上升沿的位置，记为left；获得下降沿的位置，记为right。

十字弯：当白点数目大于阈值时，认为前方路况是十字弯，理想情况和实际采集上位机显示如图11所示。

图11 十字弯

过十字弯时保持上一时刻采集到的有效赛道信息，同时微调舵机转角。

终止线：终止线的边沿总和最多。理论上有6个边沿，3个上升沿和3个下降沿，理想情况和实际采集上位机显示如图12所示。

图12 终止线

3 实验与分析

3.1 仿真实验

考虑到整个前轮转向系统的数学模型复杂，所以仿真时进行简化，将舵机近似为一阶惯性环节。研究静态时，转角对设定值的跟随情况。假设舵机的传递函数：

(9)

在Simulink搭建系统仿真图，如图13所示。

图13 前轮转向

给定输入为幅值30度的阶跃信号，模糊控制结构的仿真参数在2.1节中已介绍。为减小稳态误差，加入一个积分项，系数为0.28。由仿真结果可知静态情况下，转角输出能跟随系统输入且响应快，稳态误差小。在此情况下，为了分析模糊控制性能的优劣，用经典PID控制作仿真对比。经典PID的仿真参数为：Kp=11，Ki=1，Kd=0.05。对比如图14所示。

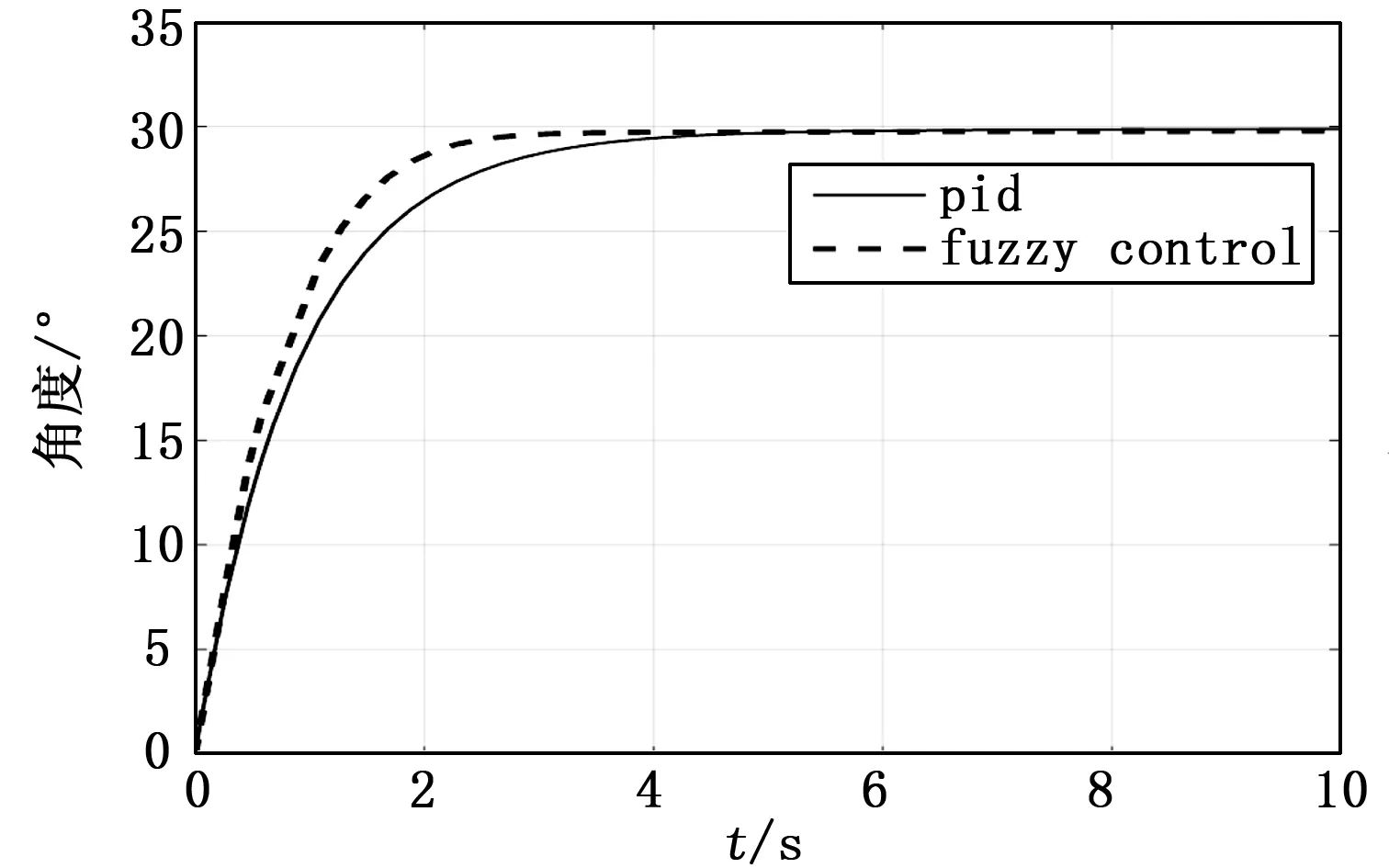
图14 PID与模糊控制对比

由图14可以看出，相比于经典PID控制，模糊控制的响应速度更快，精度更高，控制效果更优。然而实际运行时，前轮转向数学模型较仿真来说更复杂；舵机和前轮转向较难测量，机器人的位置偏差为控制输入。所以现场调试过程需要不断优化参数和控制规则。

根据2.2节建立的后轮驱动模型，将其近似为一个二阶环节，假设其传递函数为：

(10)

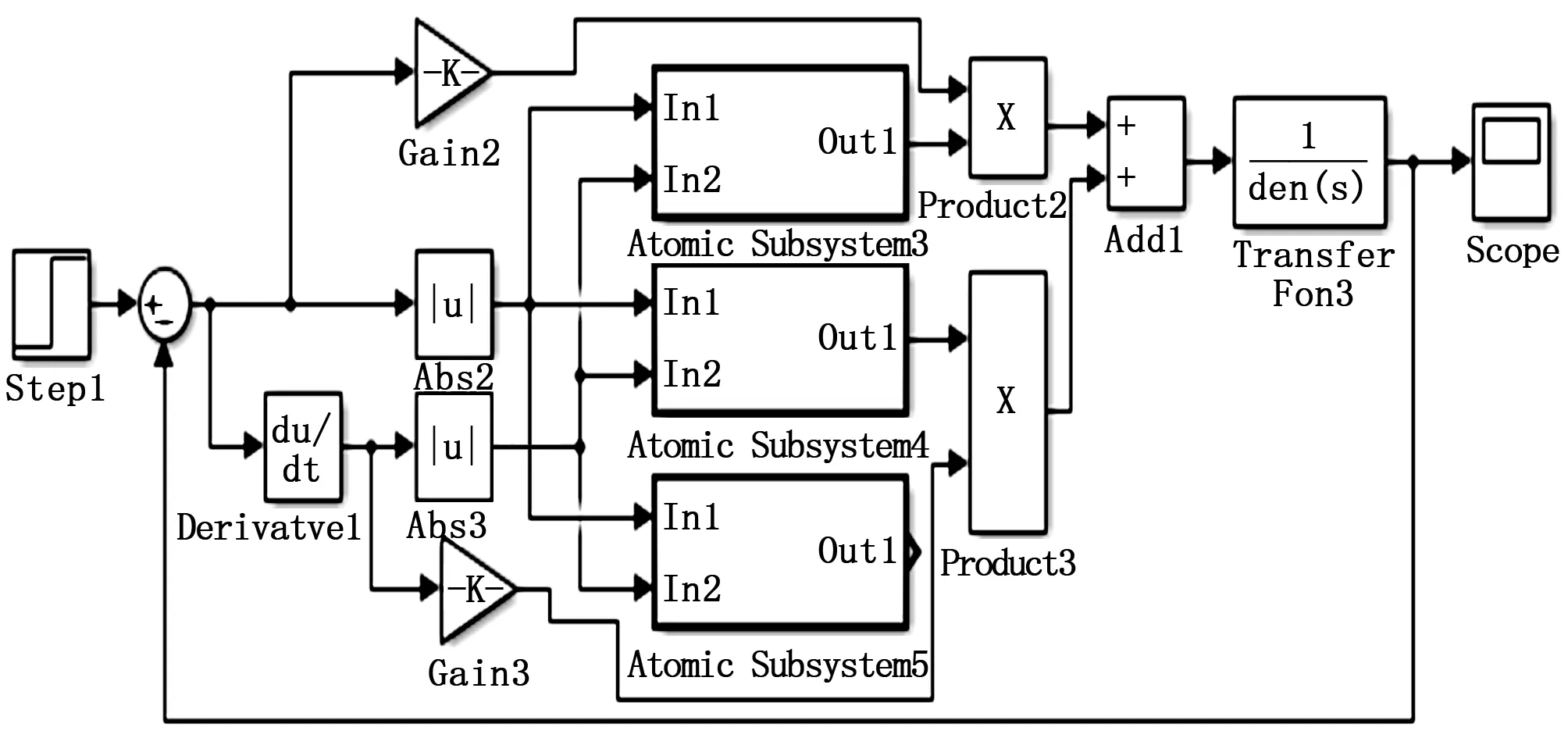
图15 智能自适应PD控制

如图15智能自适应PD控制电机：为了研究智能自适应PD控制性能，用经典PID作对比，智能自适应PD控制的Kp=106，经典PID的仿真参数为：Kp=100，Ki=0.1，Kd=0.5。给定输入为单位阶跃信号，对比结果如图16所示。

图16 PID与智能PD控制对比

由图可知PID控制能达到控制效果，但本文设计的基于解析式控制器的智能控制响应速度更快，几乎无超调。

3.2 系统联调

首先调试机器人各模块，确定无误后系统联调。调试过程中对转向和驱动模块的参数不断调整。调试舵机时关闭电源，手推机器人，观察其是否能适应不同的路况给出响应转向。舵机调试结束后上电，最终机器人能稳定地跑完全程。

4 结束语

本文在建立系统数学模型的基础上，设计了模糊控制器和解析式智能PID控制实现对机器人转向和速度的控制，设计基

于二值化灰度值的双向跳变沿检测法实现路径识别与提取，中心线寻迹法实现赛道判别与路径寻迹。实验结果表明：机器人可在不同的赛道按要求转向且速度稳定。

[1]杨 明. 无人自动驾驶车辆研究综述与展望[J]. 哈尔滨工业大学学报, 2006, 38(8): 1259-1262.

[2]吴斌华, 黄卫华, 程 磊,等. 基于路径识别的智能车系统设计[J]. 电子技术应用, 2007, 33(3):80-82.

[3]王 俊, 许 林, 岳 东,等. 基于CCD的两轮自平衡智能车系统设计[J]. 信息技术, 2013(8):179-182.

[4]张仁尊. 线性CCD智能车的控制系统设计[J]. 山东农业大学学报(自然科学版), 2016, 47(5):731-735.

[5]白晋龙. 基于线性CCD的智能车路径提取与寻迹[J]. 电子测量技术, 2016, 39(3):127-130.

[6]陈伯时. 电力拖动自动控制系统[M]. 北京: 机械工业出版社, 2003.