行为保险学系列（十一）：储蓄型保险的理性投保决策理论

郭振华 上海对外经贸大学金融学院

本文受国家自然科学基金面上项目（71173144）的资助。

保险产品分为保障型保险、保障储蓄型保险和储蓄型保险，因此，投保决策也分为保障型保险投保决策、保障储蓄型保险投保决策和储蓄型保险投保决策。本文专门研究储蓄型保险的投保决策。

本文首先对储蓄型保险进行界定，认为无论从中国还是其他多数国家来看，储蓄型保险都是寿险业保费收入最大的主力险种，对其投保决策进行研究意义重大。然后探讨人们如何进行储蓄型保险的投保决策，决策理论分为基于新古典经济学的理性决策理论和基于行为经济学的行为决策理论。本文主要探讨储蓄型保险的理性投保决策理论，下一篇将在分析理性投保决策理论缺陷的基础上讨论储蓄型保险的行为投保决策理论。

一、储蓄型保险的界定

（一）保险的分类

对消费者而言，保险产品可以分为三类：保障型保险、保障储蓄型保险和储蓄型保险。

保障型保险（媒体经常称之为消费型保险），主要是各类短期保障型保险，如各类财产保险、意外险、短期防癌险、医疗保险等，以及较为长期的定期寿险等。这类保险的特点是只有保障功能，保单没有现金价值或账户价值，没有任何投资功能。

保障储蓄型保险，指既有保障功能又有储蓄功能的保险，期限通常较长，如终身寿险、长期重大疾病保险、两全保险、年金保险等。事实上，通常只要是1年期以上保险，由于预交保费的原因，保单通常都会有现金价值，进而有储蓄功能。

储蓄型保险是指保单仅有储蓄功能没有保障功能，或虽有保障功能但保障功能几乎可以忽略不计的保险。一些万能险产品、投资连结保险产品完全没有保障功能。还有一些保险产品的保障功能几乎可以忽略不计，如几年前寿险行业销量第一的两全保险（以分红型为主）和最近几年很多寿险公司的开门红产品——年金保险，这两类保险销量极大，但多数仅提供少量的意外身故和高残保障，风险保费在总保费中的占比几乎可以忽略不计。

（二）储蓄型保险的进一步界定

首先，之所以称为储蓄型保险而非投资型保险（其实不少保险公司官网就将这些产品称为投资型保险或理财型保险），主要原因是保险公司销售的储蓄型保险其实投资风险极低，基本都有保底、有收益率甚至提供固定利率，与长期银行存款类似，称为储蓄更加合适。

其次，读者可能看出来了，保障储蓄型保险与储蓄型保险似乎很难准确区分。确实如此，因为同样类别的长期保险，保险公司既可以将其设计成保障程度较高的保障储蓄型产品，也可以将其设计成保障程度极低的储蓄型产品。以期缴保费两全保险为例，保险公司既可以将其设计成保障程度较高的产品，如疾病死亡保险金等于满期保单账户价值，意外死亡保险金等于满期保单账户价值的5倍；也可以将其设计成保障程度极低的产品，如疾病死亡保险金始终等于当时的保单账户价值，意外死亡保险金等于客户已交保费的1.5倍。即便是终身寿险也是如此，保险公司既可以将其设计成保障性很强的产品，即死亡保险金远超保单现金价值的产品；也可将其设计成保障性极弱、储蓄性极强的产品，即死亡保险金接近于保单现金价值或已交保费的产品，如近几年在银保渠道销量庞大的理财型保险，很多都是终身寿险，但保障功能极弱。

当然，为了贯彻“保险姓保”的行业发展方针，2017年4月1日之后，按照保监发〔2016〕76号文《关于进一步完善人身保险精算制度有关事项的通知》规定，保险公司开发销售的个人定期寿险、个人两全保险、个人终身寿险和个人护理保险产品，死亡保险金额或护理责任保险金额与累计已交保费或账户价值的比例应符合下表要求，而且要求死亡保险责任不能仅仅是意外身故责任，至少应当同时包括疾病身故保障责任和意外身故保障责任。

▶表 2017年4月1日后产品设计新规

显然，〔2016〕76号文较大幅度地提高了定期寿险、两全保险、终身寿险和护理保险产品的保障功能，相对弱化了这些产品的储蓄或理财功能。

但是，〔2016〕76号文并未对本来就以储蓄为主的年金保险进行约束，因此，年金保险就成为人身险公司满足客户储蓄需求的最佳选择。最近几年各大寿险公司的开门红产品纷纷选择年金产品，针对的就是客户的储蓄或理财需求，保障成分极低。

因此，本文所指的储蓄型保险，就是指短期或长期的保障成分很低甚至为零的储蓄型保险产品，其设计出发点和销售卖点都是致力于满足人们的投资理财需求而非保障需求。

二、储蓄型保险是人身保险市场的主流产品

我国人身险市场是一个以储蓄型保险为主的市场，这一点从历年的开门红产品就可以看得出来。以最近几年的开门红产品为例，各大寿险公司基本都选择了年金产品，针对的就是客户的储蓄或理财需求。

（一）我国人身保险市场以储蓄型保险为主

由于以下几点原因，从保费收入来看，我国人身保险市场以储蓄型保险为主：

第一，人身保险公司必然会追求规模保费流入，一方面可以做大公司资产规模，提高公司知名度，另一方面可以通过资产与负债的利差摊平公司成本并创造利润，这是公司股东、管理层和员工的共同追求。

第二，保障型产品如意外险、短期防癌险、短期医疗保险、定期寿险等由于件均保费很低（虽然高端医疗保险件均保费较高，但销量太少），且需求较弱，从销售来看，既无法通过互联网渠道获取大量的客户和保费，也无法通过代理人渠道作为主险进行销售，无法成为人身险公司的主要保费流入产品。

第三，保障储蓄型保险，如保障功能较强的终身寿险、长期或终身重疾险、长期护理保险、养老年金保险等。这些产品，除重疾险的需求较为强劲外，其他产品的需求都比较疲弱，也无法成为人身险公司的主要保费流入产品。

第四，我们不得不承认，人们对储蓄、投资的需求远超过对保障的需求，或者说，储蓄带给人们的边际效用远超过保障带给人们的边际效用。

第五，正是因为人们对长期保障储蓄型保险的需求比较疲弱，而人身保险公司又要追求保费规模和资产规模，人身保险公司在产品开发上就逐渐将这些产品调整为满足监管最低保障需求的储蓄型产品，如将终身寿险开发成理财型万能险，将养老年金产品逐渐设计成即交即领（现在是期满5年后领取，但第一笔领取金额正是之前同类产品前5年的领取总额）的年金保险等，目的就是突出产品的投资收益竞争力，满足客户的储蓄需求。

第六，储蓄决策的关键就是利率或投资收益率，因此，为了提高产品竞争力，保险公司不得不尽可能降低保单保障水平，降低保费中包含的风险成本，以便提升客户保费投入的投资收益率，这正是保险公司在产品设计中遵循的潜在原则。

正是在上述原因决定的思维方式下，我国人身保险公司将产品进行了大量的改进，对难以通过保障这个卖点进行销售的保障储蓄型产品如终身寿险、长期护理保险、养老年金保险等，尽量降低保障程度，将卖点集中在储蓄利率或投资收益率上。

以年金保险为例，10多年前，寿险公司们开发的多数是传统养老保险产品，即购买时分期交费、退休后才领取养老金的养老保险，可惜客户根本不买账，销量很少，导致寿险公司们纷纷转向了更偏理财功能、期限更短的两全保险，导致两全保险（分红型）有几年长期位居销量榜首。但最近几年，年金保险逐渐成为多数寿险公司的主流产品或开门红产品，销量大增，但现在流行的年金保险产品已经与传统养老年金保险截然不同了。以某公司的开门红产品为例，主险是一款分红型年金保险，客户分期交纳保费后，保险公司在第5个保单年度末返还总保费的约10%，然后从第六年开始每年返还总保费的约2%，直至被保险人身故，身故时返还客户所交总保费，此外，在保险期间，每年根据公司经营状况给客户进行分红。这看起来像是保险公司发行的一款保底收益率为2%的长期债券，期间每年支付利息，期末返还本金，这就使得传统养老年金保险的互助功能或保障功能基本丧失了。当然，这类保险也会提供少许保障功能，如提供缴费期意外身故或全残的保费豁免功能，但风险保费占比极低。这就使得年金保险在本质上变成了一个长期储蓄产品。这就是人类本性对保险产品的塑造，是基于人类本性的保险需求与相对理性的保险供给不断互动的结果。

也就是说，从保费收入来看，我国人身保险市场的主流产品其实一直都是储蓄类产品，较早的是两全保险为主，然后逐渐转变为年金保险为主。

（二）全球寿险市场基本都是以储蓄险为主

不过，从全球寿险市场来看，长期储蓄型产品都是主流。例如，根据瑞士再保险公司研究部Sigma2012年第1期《了解寿险业盈利状况》中提供的主要保险市场的寿险产品结构显示，按照2010年保费收入数据来看，德国、美国、英国和日本这全球四大寿险市场基本都是以储蓄为主的，尤其是以养老储蓄为主。

2010年，德国寿险市场中，只有约2%的保障型保险保费收入（定期保险、抵押补偿保险和支付保障保险）和5%的意外和健康险保费收入（失能保险、长期护理保险），但有33%的养老金和年金（养老金和年金保险）及60%的储蓄（两全保险和养老储蓄）。

2010年，美国寿险市场中，有约26%的意外和健康险保费收入（失能保险、长期护理保险、重疾险和医疗费用保险）、23%的寿险保费收入（定期寿险、终身寿险、万能寿险和变额万能寿险）和51%的年金保费收入（固定年金和变额年金）。

2010年，英国寿险市场中，有1%的意外和健康险保费收入、4%的保障保费收入（定期寿险）、12%的储蓄保费收入（投资产品、养老保险）及83%的养老金和年金收入（养老金、退休收入产品）。

2010年，日本寿险市场中，意外和健康险保费收入几乎为零，有72%的寿险保费收入（67%的个人寿险，5%的团体寿险，寿险包括定期寿险、终身寿险、养老保险和团体信用寿险）和28%的年金（13%的团体年金、15%的个人年金，年金包括固定年金和变额年金）。

这不足为奇，寿险市场不可能仅仅依赖销售件均保费很低、需求却又疲弱的保障型保险来获得如此大的保费规模和资产规模。

三、储蓄型保险的理性投保决策理论

既然储蓄型保险的卖点就是储蓄利率或投资收益率，储蓄型保险的决策理论其实就是储蓄决策理论。只不过，储蓄型保险的储蓄期限可长可短，而且多数储蓄型保险都比一般的银行储蓄要长。以现在市场上最流行的终身年金为例，如果被保险人为零岁，就相当于购买了105年期的长期储蓄。

（一）理性人如何规划储蓄

人们为何要储蓄呢？按照经济学理论，理性的消费者会追求一生效用的最大化，或者说，理性人会妥善安排自己的一生的活动以获得最大的享受。为了达到这个目标，理性人需要合理分配自己的终身收入，以获得理想的终身消费模式，这就意味着消费者必须为未来尤其是失去劳动能力或退休后做好规划而不能只考虑当前。

用于解释消费者应该如何规划当前消费和未来储蓄的、被广泛接受的两个理论分别是生命周期假说和持久性收入假说。安东和莫迪利亚尼1963年提出的生命周期假说认为，个人在开始工作期间收入较低，壮年时期收入较高，退休后则没有收入，于是，理性人会在壮年时期进行储蓄，为退休后的消费积累资金。这看起来像是常识，但安东和莫迪利亚尼的实质贡献是将这一理念处理为一个正式的模型——用于消费和储蓄研究的生命周期模型。与生命周期假说类似，诺奖得主弗里德曼1975提出的持久收入假说认为，理性人希望拉平自己一生的消费水平，并通过评估自己的持久性收入来做到这一点。所谓持久性收入，是指个体会将其未来所有劳动收入在一生中进行均衡分配，确保其一生保持不变的消费支出水平，这一不变的消费支出水平就是其持久性收入。弗里德曼的意思是说，个体应该将壮年时期收入超出持久性收入的部分进行储蓄。

（二）储蓄型保险的理性投保决策理论

从我国保险市场来看，个人购买的储蓄型保险主要是固定利率产品和有保底收益率的产品，类似于银行储蓄，投资风险极低。所以，按照金融学理论，理性的消费者会使用折现现金流模型计算储蓄型保险的内部收益率或投资收益率，然后将其与长期银行存款利率进行对比，如果收益率超过银行存款利率，就会决定投保，反之则不会投保。

假定有如下一款简单的5年期缴费的终身年金保险：被保险人30岁，年交保费A元，连续交5年；保险利益为，从第一个保单年度末开始，每个保单年度末均领取保险金B元，直至死亡为止。假定长期银行存款利率为3.5%（已折算成复利），理性消费者该投保这一年金保险吗？

假定该被保险人的预期寿命为85岁，则可以根据公式（1）计算购买该年金获得的内部收益率i，如果i＞3.5%，就选择投保，反之则选择不投保。

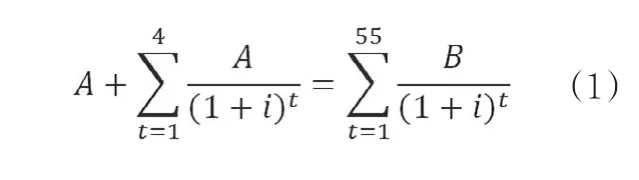
四、折现现金流模型的起源：贴现效用模型

在上述计算内部收益率时用到的折现现金流模型，其根源是1937年萨缪尔森提出的贴现效用模型。那么，贴现效用模型又是如何起源和发展并成为经济学中的标准化跨期决策模型的呢？

（一）贴现效用模型的起源

跨期选择是对发生于不同时期的成本与收益进行权衡的决策行为。在日常生活中，许多决策或选择行为都涉及跨期情形，如储蓄和投资决策、健身和减肥决策、空调或电暖器购买决策、政府基建项目决策、企业长期投资决策、企业新产品开发决策等。

跨期资源配置有多种类型，有的资源投入和产出均为货币，如储蓄和投资决策；有的资源投入为货币和非货币的组合，产出是非货币的（时间、精力等），如健身或减肥决策；有的资源投入为货币，但资源产出是非货币和货币的组合（温暖、舒适、节能等），如空调购买决策。在进行上述各种决策时，通常都会涉及长时期的资源投入和产出，因此称为跨期决策或跨期选择。

从《国富论》算起，亚当·斯密是首位对跨期选择的重要性进行讨论的经济学家。之后，约翰·雷（John Rae，1834）首次为跨期选择理论提供了心理学基础，约翰·雷在其专著《资本的社会学理论》中提出：“‘对积累的有效欲望’是决定一个社会实施储蓄与投资的关键心理因素，这进而决定了一国经济的生产率和增长率。”约翰·雷还提出了四个增进或抑制积累欲望的心理因素，其中，能够增进积累欲望的两个因素是“对后代的遗赠动机和自我克制的倾向”，能够抑制积累欲望的两个因素是“人生的不确定性和及时享乐的欲望”。

之后，波希姆-鮑沃克（Böhm-Bawerk，1889）和庇古（Pigou，1920）提出：人们通常会低估未来的欲望或效用，这导致人们有偏向于当前的时间偏好。此外，波希姆-鮑沃克还为跨期决策理论提供了创新思想“时间偏好”，认为跨期选择可被视为个体在不同时期配置资源的取舍行为，这与在当前的在不同的商品消费之间进行取舍的行为是类似的，后者是个体的商品偏好，前者是个体的时间偏好。

之后，欧文·费雪（Irving Fisher,1930）对上述研究工作尤其是波希姆-鮑沃克的创新思想进行了规范化处理，用无差异曲线规范地描述和拓展了波希姆-鮑沃克的分析框架，从而将跨期选择纳入了效用最大化的标准经济学分析体系。其中，当前消费用横轴表示，未来消费由纵轴表示，当前消费与未来消费的边际替代率由时间偏好和边际效用递减率共同决定。

皖河流域地势西北高，东南低，地貌上有明显的阶梯状特征。从图1可见，合九铁路自西北向东南经过流域中部，铁路沿线属大别山前缘岗地和丘陵。沿线西北侧有东北—西南向断层崖。以崖为界，西北属皖河流域上游山地，大部分归属太湖、岳西和潜山3县。东南侧为低山丘陵至沿江平原。按山、丘、圩、湖划分，山土面积3 337 km2，占51.8%，丘陵面积1 689 km2，占26.2%，圩区面积1 021 km2，占15.9%，主要河湖水面面积394 km2，占6.1%。

最后，1937年，萨缪尔森在一篇题为《略论对效用的计量》（A note on measurement of Utility）的短文中，提出了贴现效用模型，将费雪的无差异分析曲线分析从仅限于两时期扩展到多时期。该模型最大的特点，是用贴现率这个单一参数代表了所有与时间偏好有关的心理因素。

（二）贴现效用模型的形式

贴现效用模型的基本形式为：在多时期情形下，个体面临的跨期决策问题是，如何对未来多期消费束（c0，c1，…，cT）进行选择。在偏好满足完备性和传递性的前提下，处于时期0的个体面临的跨期总效用函数可表达为U0（c0，c1，…，ct），并假设：一是效用可以实施基数计量，二是个体的跨期总效用可拆分为由各期“子效用”贴现加总的形式，三是每期效用均在期末获取而非每期期间不断获取，由此，萨缪尔森将跨期总效用表达为：

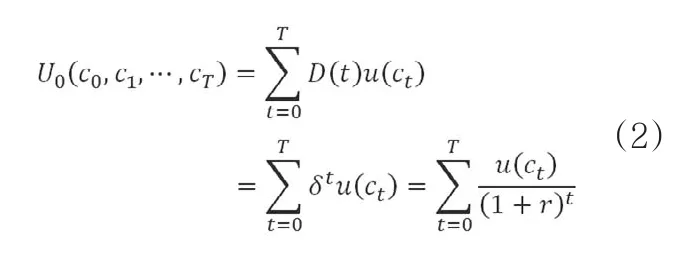
其中，c0，c1，…，cT表示从时期0到时期T的消费计划；

U0（c0，c1，…，cT）表示从时期0到时期T的消费计划c0，c1，…，cT在当下或时期0的总效用；

u(ct)可以被理解为个体在时期t消费ct所获得的瞬时效用；

D(t)=δt是个人的贴现函数，表示在时期0时，个体对时期t获得的效用所赋予的权重，或者说，时期0，1，2，…，T的效用将分别以1，δ，δ2，…，δT的比例折现；

r表示个体对未来效用的贴现率，也称时间偏好率，在萨缪尔森的模型中，r是逐期固定不变的；

δ=1/（1+r）是每期贴现因子，用每期贴现因子乘以时期t+1的效用就可以得到这些效用贴现到时期t的值。

有了这个总效用计算公式，就可以据此计算不同选择方案的跨期总效用，进而选择总效用最大的方案，这就将多时期的跨期选择行为用标准经济学模型，即效用最大化模型进行了描述。

贴现效用模型看起来不复杂，但却蕴含了对人类跨期决策行为的深刻思考：

第一，通常，贴现率r为正值，于是每期贴现因子δ=1/（1+r）＜1，这就意味着，对于不同时期的相同的消费额、消费效用或现金流入，人们总是偏好现在甚于将来，或者说，人们对现在的关心程度总是高于对未来的关心程度，这是人类最基本的时间偏好特性。

第二，随着时期向后延展，由于δ＜1，个体的贴现函数δt将逐渐缩小，即1＞δ＞δ2＞，…＞δt，因此，未来越久远，当下人们对其关心程度就越低。例如，当贴现率r=10%时，第5、10、15、20、25、30、35、40期的δt值分别为0.621、0.386、0.239、0.149、0.092、0.057、0.036、0.022，这说明，到40期时，贴现函数已经接近于零了，这表明，个体对第40期及以后的效用基本就不太关心了。

第三，贴现效用模型中的每期瞬时效用具有边际递减的特性，即每期瞬时效用u'＞0且u"＜0，这使得每期瞬时效用函数有如下性质：

u（xt+xt+1）＜u（xt）+u（xt+1）

其含义是，将资源集中在某一期消费所带来的效用，低于将这些资源分摊到各期消费所带来效用。也就是说，只要个体服从边际效用递减律，他就有将一些资源推迟到未来消费的动机。

总体而言，贴现率r为正反映了人们更加看重当下的动机，而边际效用递减则反映了人们也有动机延后消费，个体最终决策是两种力量相互折中的结果。

（四）贴现效用模型的规范性地位：理性人的跨期决策方法

贴现效用模型不仅是标准经济学模型，即贯彻效用最大化思维模式的模型，而且，该模型还获得了规范性的地位，即理性人就应该据此进行跨期决策的模型。因为新古典经济学认为理性人的偏好是一致的，反之，偏好不一致通常属于非理性行为，而萨缪尔森贴现效用模型符合动态一致性。

贴现效用模型符合动态一致性主要体现在两方面：一是未来各期的折现率是固定不变的；二是个体的瞬时效用函数也是稳定不变的，这两点导致按照该模型进行决策的个体在行为选择上体现了动态一致性，即无论在哪个时点上，个体对各种选择结果的偏好顺序都是稳定不变的，今天偏好A甚于B（如今天爱吃西餐甚于中餐），未来各期也是如此（未来各期也都是爱吃西餐甚于中餐）。

五、折现现金流模型：理性人的储蓄决策方法

如前所述，折现现金流模型的根源是贴现效用模型，那么贴现效用模型是如何变化为金融学领域流行的折现现金流模型呢？

在贴现效用模型基础上，再做进一步的假设：假设未来每期等量的花费都会带来等量效用，u（ct）=ct，即未来消费支出 ct带来的效用即为ct，于是，贴现效用模型中的分子也可以用未来净现金流入代替，按照假定，现金流入额就等于等量效用获得额，由此，贴现效用模型就变成了折现现金流模型：

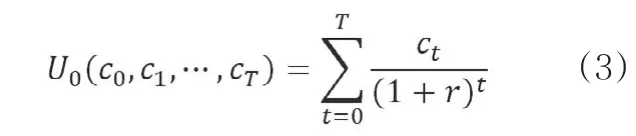
其中，ct表示第t期的现金流入。显然，现金流入为正时ct为正，现金流入为负时ct为负。

例如，假定未来三年会获得三笔现金流入（2000,2000,2000），假定相应带来的效用也为（2000,2000,2000），折现率每年均为10%，则未来各期现金流入的当前效用之和为：

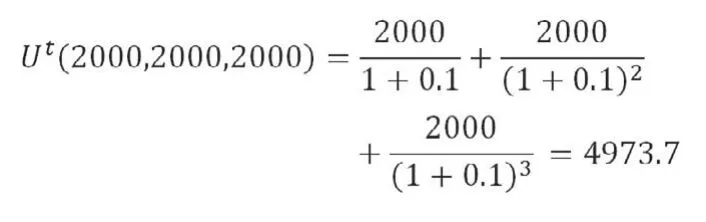
可以看出，这种计算贴现效用的方式就与金融学中计算净现值的复利折现现金流公式非常类似了，至少在形式上已经完全相同了。唯一的区别是：贴现效用模型的分子是未来各期瞬时效用，折现现金流模型的分子是未来各期现金流。

因此，金融学中的折现现金流模型其实就是经济学中贴现效用模型在金融学中的运用，即在资源投入和产出均为货币情形下的运用。将萨缪尔森贴现效用模型用于跨期决策时，考虑的是在相同的投入下，有不同的选择方案，哪个方案的贴现总效用最大，就选择哪个方案；在将折现现金流模型用于储蓄决策时，采用的净现值准则，类似于贴现效用模型的思维，就是在假定参照收益率的情况下计算未来现金流入的总现值，然后与当期现金投入比较，如果净现值大于零，就选择这项储蓄。当然，储蓄行为也可以采取内部收益率法进行决策，即计算这项储蓄的内部收益率，然后与参考收益率进行比较，高于参考收益率，就选择该项储蓄，其实只是净现值准则的变形而已，内在原理都与贴现效用模型相同。

如上所述，与贴现效用模型类似，折现现金流模型也是金融学中储蓄决策的理性决策模型，当然也是储蓄型保险的理性投保决策模型。