考虑液滴形状影响的气井临界携液流速计算模型

潘 杰 王武杰 魏耀奇 陈军斌 王亮亮

1.西安石油大学石油工程学院/博士后创新基地 2. 中国石油大学（北京）石油与天然气工程博士后科研流动站3.中国石油长庆油田公司第四采气厂

在有水气藏开发中后期，气藏压力逐渐降低、气井产水量逐渐增大，使得气流难以携带井底产出水到达地面，从而在井底产生积液[1]。气井积液会增大井底回压，导致气井产量下降，严重时甚至会压死气井造成停产[2-3]。国内外学者针对气井积液提出了不同的临界携液流速计算模型。Turner等[4]根据质点力平衡理论首次提出了气井连续携液计算模型，但其预测值偏大。此后，许多学者对Turner模型进行了修正[5-8]，其中李闽模型[6]在国内得到了广泛应用。王志彬和李颖川[9]、周瑞立等[10]和熊钰等[11]基于椭球形液滴假设分别建立了具有良好通用性的临界携液流速计算模型。谭晓华和李晓平[12]基于液滴总表面自由能与气流总湍流动能的相等关系，建立了临界携液流速计算模型，但是该模型并没有考虑液滴变形以及变形对液滴表面自由能的影响。本文基于液滴总表面自由能与气流总湍流动能的相等关系，建立了考虑液滴直径、液滴变形及变形对液滴表面自由能影响的气井临界携液流速计算模型。

1 模型建立

Taitel等[13]认为：液滴尺寸由使其破碎的湍流力和使其保持完整的表面张力共同决定。在气井井筒雾状流条件下，液相主要以液滴的形式存在，当气相湍流力大于气液相界面的表面张力时，液滴将破碎为更小直径的液滴；反之，当气相湍流力小于气液相界面的表面张力时，液滴会发生聚并，形成较大直径的液滴。由此可知：稳定存在的最大液滴，其湍流力与表面张力相等。受迎风面与背风面压差影响，气流中液滴会发生微小变形[1]，从而随气相雷诺数的改变呈现出不同的液滴形状。液滴变形会直接导致：①迎风面面积增加，曳力系数增大，液滴更易于被气流携带；②单液滴的表面自由能增加，在气相总湍流动能不变时，液滴最大直径也相应增大。本文在建立模型时做出以下假设：①液相全部以最大液滴的形式存在；②液滴为椭球形，如图1所示。

基于上述假设，分析了液滴变形对液滴的最大迎风面直径、临界携液流速、曳力系数的影响，提出了新的临界韦伯数与液滴变形参数的函数关系式，并采用了考虑压力和温度影响的表面张力计算公式，最终建立了考虑液滴形状影响的气井临界携液流速计算模型。

1.1 液滴最大迎风面直径

液相受气流剪切作用会在井筒内形成一定数量的液滴，单位时间所对应的液滴数目如下：

图1 液滴变形及受力分析示意图

式中N表示液滴数目，个；vsl表示液相表观流速，m/s；A表示流道截面面积，m2；d表示液滴的迎风面直径，m。

液滴变形参数定义如下：

式中K表示液滴变形参数，无量纲；dE为椭球形液滴的迎风面直径，m；dB为球形液滴的直径，m。

单液滴表面积可按下式计算：

式中s表示单液滴表面积，m2；h表示椭球形液滴的短轴长度，m。

由于液滴变形后体积不变，因此有：

将式（4）代入式（3），则单液滴表面积可进一步表示为：

故液滴的总表面积计算如下：

式中S表示液滴总表面积，m2。

Adamson等[14]指出单位时间内液滴的总表面自由能可按下式计算：

式中Es表示液滴总表面自由能，W；σ表示气液界面的表面张力系数，N/m。

因此，单位时间内液滴的总表面自由能为：

White 指出单位时间所对应的单位体积内气相湍流动能为：

式中eT表示单位体积气相的湍流动能，W/m3；ρg表示气体密度，kg/m3； 表示径向脉动速度，m/s；表示切向脉动速度，m/s； 表示轴向脉动速度，m/s。

考虑到井筒内通常为湍流，且雷诺数较大，可认为流动具有各向同性，即因此

故单位时间连续气相的总湍流动能为：

式中ET表示气相总湍流动能，W；vsg表示气相表观速度，m/s。

Taitel和Dukler[16]指出，径向湍流脉动速度的均方根约等于摩擦速度，如下式：

式中v*表示摩擦速度，m/s；fsg表示气相表观流速下的摩擦系数。

将式（12）代入式（11）可得：

根据液滴的总表面自由能与气相总湍流动能相等的关系，可以得到液滴最大迎风面直径计算如下：

式中当K＝1时，d表示球形液滴的直径，m；当K≠1时，d表示椭球液滴的迎风面直径，m。

1.2 临界携液流速

在垂直井筒中，液滴受浮力、曳力和重力的共同作用（图1），在临界携液流速条件下单个液滴受力处于平衡状态，即

式中Fg表示浮力，N；FD表示曳力，N；G表示重力，N。浮力计算公式为：

式中g表示重力加速度，m/s2。

重力计算公式为：

式中ρl表示液滴密度，kg/m。

曳力计算公式为：

式中CD表示曳力系数；SE表示液滴的迎风面面积，m2；Δp表示液滴迎风面与背风面所受压差，Pa。

椭球形液滴的迎风面面积可按下式计算：

根据Bernoulli方程，液滴迎风面与背风面所受压差：

式中vc表示临界携液流速，m/s。

将式（19）、（20）代入式（18）中，可得椭球形液滴的曳力计算公式为：

将式（16）、（17）和（21）代入式（15）中，整理可得：

根据Orkiszewski[17]流动形态界限判别法和流型过渡准则[18]，临界携液流速的表达式可进一步表示为：

气体临界携液流量表示如下：

式中qc表示临界携液流量，m3/d；Z表示气体压缩系数；T表示热力学温度，K；p表示压力，MPa。

1.3 曳力系数

曳力系数与液滴形状和雷诺数（Re）有关[11]。已有的曳力系数经验公式较多，包括经Brown和Lawler[19]验证过的Clift & Gauvin模型[20]、Flemmer& Banks模型[21]、Khan & Richardson模型[22]、Haider & Levenspiel模型[23]，以及GP模型[24]、邵明望模型[25]和Brauer模型[26]。本文参考文献[11,27]认为Brauer模型[26]的拟合效果最好。图2给出了上述模型计算的曳力系数值随雷诺数的变化曲线。对比发现经Brown和Lawler验证过的前四种模型计算结果比较接近。在Re＜100时，Brauer模型、GP模型、邵明望模型的计算值偏差不大，但随着Re的增大，邵明望模型的计算值急剧减小，与其他模型计算的结果差异较大。当Re＜2×103时，Brauer模型和GP模型的计算结果比较接近。随Re的增加，Brauer模型的计算值变化不大，在0.40～0.41之间，这也解释了基于球形液滴假设的临界携液流速模型一般将曳力系数值取在0.4左右的原因。在高雷诺数（2×105≤Re＜1×106）范围内，GP模型的计算结果偏小，可靠性较低。本文分别将GP模型[24]、邵明望模型[25]、Brauer模型[26]和Clift & Gauvin模型[20]的拟合计算公式进行验算，将结果与气井实际生产数据对比后发现针对气井井筒的高雷诺数湍流流动，Brauer模型的计算结果最为准确。

图2 不同模型曳力系数计算结果对比图

上述模型均是基于刚性球体得到的，但是液滴变形后并非球体，且液滴内部流动的影响也势必使得曳力系数值与上述模型计算的结果有偏差。Liu和Reitz[28]认为扁平体曳力系数是圆球体的3.632倍，椭球体的曳力系数介于扁平体与刚性球体之间。Helenbrook和Edwards[29]指出由于液滴内部流动的影响使得液滴较相同尺寸的刚性球体的曳力系数小。王志彬和李颖川[9]将球形颗粒在高雷诺数的曳力系数（0.424）降低15%作为刚性椭球的曳力系数，并综合考虑液滴变形和液滴内部流动对其进行修正，得到椭球体的曳力系数表达式为：

本文将Brauer模型基于圆球体的曳力系数计算值增大20%，作为变形椭球体的曳力系数，即

1.4 临界韦伯数与液滴变形参数

临界韦伯数受气相流速与液相流速的影响，一般采用下式计算[30]：

式中Wec表示临界韦伯数；λ表示中间变量，；Gle表示液滴的质量流量，kg/（m2·s）。

液滴变形参数一般通过临界韦伯数确定。王志彬和李颖川[9]利用麦夸特法和通用全局优化法拟合并提出临界韦伯数和液滴变形参数的函数关系式为：

熊钰等[11]提出的临界韦伯数和液滴变形参数的函数关系式为：

采用本文参考文献[31]给出的椭球表面积计算公式计算液滴内能的增量，并忽略液滴之间的传热与传质，基于能量守恒原理建立了新的临界韦伯数和液滴变形参数函数关系式：

图3对本文提出的液滴变形参数模型和王志彬和李颖川[9]提出的模型进行了比较，认为整体符合程度较好，在Wec=1时，两者相对误差为－11.7%。但本文模型同时避免了熊钰所提出模型存在的复杂积分求解以及王志彬计算模型存在的变形参数高次项的解析计算过程。考虑到王志彬建立的模型，其变形参数取最大液滴破碎时的值，而尺寸略小的液滴只发生变形而不会破碎，且变形程度不如大液滴。因此将本文提出的液滴变形参数模型计算结果下调10%。

图3 液滴变形参数与临界韦伯数的关系曲线图

1.5 气液界面的表面张力

工程应用中，Turner等[4]推荐气液界面的表面张力为0.06 N/m。但表面张力会随压力和温度变化而改变，本文在模型验证过程中，采用本文参考文献[32]给出的考虑压力和温度影响的表面张力计算公式为：

式中σ表示温度为t ℃时水的表面张力，mN/m；t表示温度，℃；σ(23.33)表示温度为23.33 ℃时水的表面张力，σ(23.33)=76 exp(－0.036 257 5 p)，mN/m；σ(137.78)表示温度为137.78 ℃时水的表面张力，σ(137.78)=52.5－0.870 18 p，mN/m。

2 模型对比与实例验证

表1对常见的临界携液模型进行了对比。Turner模型[4]、李闽模型[6]和王毅忠模型[7]都将液滴视为刚性体，并给定曳力系数的值，最终模型表达式的系数为定值；王志彬模型[9]、熊钰模型[11]和本文模型均考虑了液滴的连续变形，且曳力系数采用气井实际参数计算获得，因此表达式的系数不再是常数。

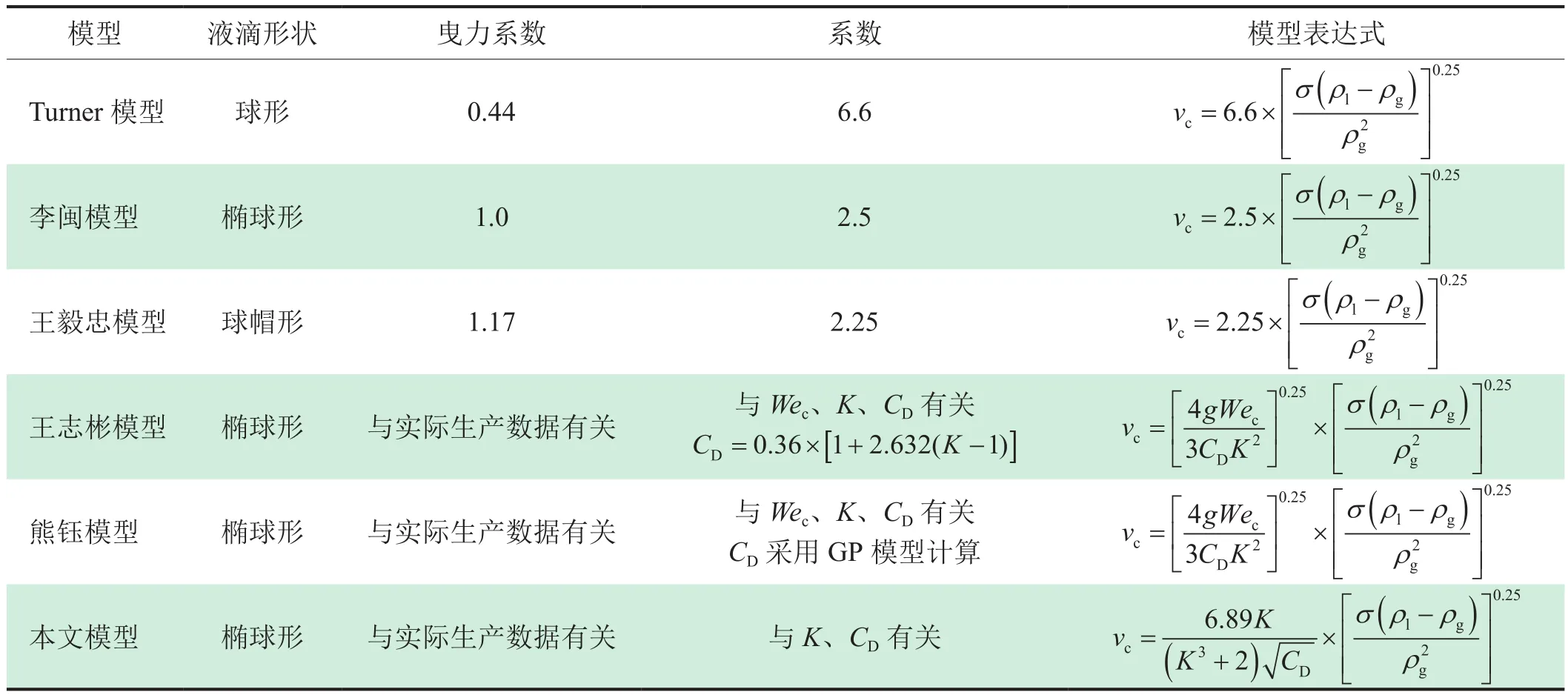
表1 气井临界携液模型对比表

分别采用上述模型对现场44口气井是否积液进行了预测。其中15口气井的生产数据来自本文参考文献[6]，井筒的平均温度取322 K，平均压缩因子取0.845，29口气井的生产数据来自本文参考文献[33]，井筒的平均温度取310 K，平均压缩因子取0.8。采用的气井基础数据如下：油管内径为0.062 m，天然气相对密度的平均值取0.6，矿化水密度取1 074 kg/m3，气水界面张力按式（31）计算。天然气密度均采用下式计算[6]：

式中γg表示天然气相对密度。

图4和图5将不同临界携液模型的计算结果和气井实际情况进行了比较。图中积液气井临界携液流量计算结果处于对角线上侧或者未积液气井预测值处于对角线下侧，即认为模型对积液判断正确，否则认为判断错误；对接近积液的气井，预测值与实际产气量的偏差处于±15%内（图中2条虚线之间）即认为模型预测结果与气井实际情况符合，否则认为预测结果偏大或偏小。从图4可以看出，Turner模型[4]得到的临界携液流量明显偏大。熊钰模型[11]由于采用了GP模型，高雷诺数气井流动状态下求解的曳力系数值过小，导致其预测值也偏大。两者对9口接近积液的气井，其预测值远大于实际产气量，且均对16口未积液气井全部产生误判。王志彬模型[9]的临界携液流量预测值小于Turner模型[4]和熊钰模型[11]，但对9口接近积液气井的预测结果同样偏大，且对9口未积液气井产生误判。王毅忠模型[7]的预测结果略有偏小，对1口积液气井产生误判，对6口接近积液气井的预测偏差超出±15%范围。本文模型和李闽模型[6]的预测结果比较接近，两者对积液和未积液气井全部判断正确。对接近积液的9口气井，本文模型的计算结果与气井实际情况符合更好，仅有1口气井的预测偏差超出±15%范围，平均偏差仅为7.8%，小于李闽模型10%的平均偏差。

图4 Turner模型、熊钰模型和王志彬模型计算结果对比图

图5 李闽模型、王毅忠模型和本文模型计算结果对比图

3 结论

1）基于能量守恒原理建立了新的临界韦伯数和液滴变形参数函数关系式，与现有计算模型相比，计算结果整体符合程度较好，同时可避免熊钰模型存在的复杂积分求解以及王志彬模型中烦琐的变形参数高次项的解析求解过程。

2）新模型综合考虑了液滴直径、液滴变形及变形对液滴表面自由能的影响，临界携液流速计算模型表达式的系数不再为常数，而与液滴变形参数与曳力系数有关。

3）结合现场44口气井实际生产情况，将本文模型与现有临界携液流速模型进行了验证，结果表明本文模型的预测结果与气井实际状况符合最好，可用于气井积液的判断。

[1] 魏纳, 李颖川, 李悦钦, 刘安琪, 廖开贵, 俞欣. 气井积液可视化实验[J]. 钻采工艺, 2007, 30(3): 43-45.Wei Na, Li Yingchuan, Li Yueqin, Liu Anqi, Liao Kaigui & Yu Xin. Visual experimental research on gas well liquid loading[J].Drilling & Production Technology, 2007, 30(3): 43-45.

[2] 刘双全, 吴晓东, 吴革生, 王效明, 王选茹. 气井井筒携液临界流速和流量的动态分布研究[J]. 天然气工业, 2007, 27(2):104-106.Liu Shuangquan, Wu Xiaodong, Wu Gesheng, Wang Xiaoming &Wang Xuanru. A study on dynamic distribution of the liquid-carrying critical velocities and ぼow rates along the wellbore of gas wells[J]. Natural Gas Industry, 2007, 27(2): 104-106.

[3] 叶礼友, 高树生, 杨洪志, 熊伟, 胡志明, 刘华勋, 等. 致密砂岩气藏产水机理与开发对策[J]. 天然气工业, 2015, 35(2): 41-46.Ye Liyou, Gao Shusheng, Yang Hongzhi, Xiong Wei, Hu Zhiming, Liu Huaxun, et al. Water production mechanism and development strategy of tight sandstone gas reservoirs[J]. Natural Gas Industry, 2015, 35(2): 41-46.

[4] Turner RG, Hubbard MG & Dukler AE. Analysis and prediction of minimum ぼow rate for the continuous removal of liquids from gas wells[J]. JPT, 1969, 21(11): 1475-1482.

[5] Coleman SB, Clay HB, Mccurdy DG & Lii LN. A New look at predicting gas-well load-up[J]. JPT, 1991, 43(3): 329-333.

[6] 李闽, 孙雷, 李士伦. 一个新的气井连续排液模型[J]. 天然气工业, 2001, 21(5): 61-63.Li Min, Sun Lei & Li Shilun. A new gas well liquid continuous withdrawal model[J]. Natural Gas Industry, 2001, 21(5): 61-63.

[7] 王毅忠, 刘庆文. 计算气井最小携液临界流量的新方法[J]. 大庆石油地质与开发, 2007, 26(6): 82-85.Wang Yizhong & Liu Qingwen. A new method to calculate the minimum critical liquids carrying ぼow rate for gas wells[J]. Petroleum Geology & Oilベeld Development in Daqing, 2007, 26(6):82-85.

[8] 刘刚. 气井携液临界流量计算新方法[J]. 断块油气田, 2014,21(3): 339-340.Liu Gang. A new calculation method for critical liquid carrying flow rate of gas well[J]. Fault-Block Oil & Gas Field, 2014,21(3): 339-340.

[9] 王志彬, 李颖川. 气井连续携液机理[J]. 石油学报, 2012,33(4): 681-686.Wang Zhibin & Li Yingchuan. The mechanism of continuously removing liquids from gas wells[J]. Acta Petrolei Sinica, 2012,33(4): 681-686.

[10] 周瑞立, 周舰, 罗懿, 李璇, 刘玉祥. 低渗产水气藏携液模型研究与应用[J]. 岩性油气藏, 2013, 25(4): 123-128.Zhou Ruili, Zhou Jian, Luo Yi, Li Xuan & Liu Yuxiang. Research and application of liquid-carrying model for low permeability and water production gas reservoir[J]. Lithologic Reservoirs, 2013,25(4): 123-128.

[11] 熊钰, 张淼淼, 曹毅, 鲜波, 卢怡. 一种预测气井连续携液临界条件的通用模型[J]. 水动力学研究与进展: A辑, 2015,30(2): 215-222.Xiong Yu, Zhang Miaomiao, Cao Yi, Xian Bo & Lu Yi. A universal model of prediction for critical continuous removal of liquids from gas wells[J]. Chinese Journal of Hydrodynamics, 2015,30(2): 215-222.

[12] 谭晓华, 李晓平. 考虑气体连续携液及液滴直径影响的气井新模型[J]. 水动力学研究与进展: A辑, 2013, 28(1): 41-47.Tan Xiaohua & Li Xiaoping. Gas wells model of continuous removal of liquids through a new estimation of droplet diameter[J].Chinese Journal of Hydrodynamics, 2013, 28(1): 41-47.

[13] Taitel Y, Bornea D & Dukler AE. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes[J].AIChE Journal, 1980, 26(3): 345-354.

[14] Adamson AW & Gast AP. Physical chemistry of surfaces[M]. 6thed. New York: John Wiley & Sons Inc, 1997.

[15] White FM. Viscous ぼuid ぼow[M]. 2nded. New York: McGraw-Hill Higher Education, 1991.

[16] Taitel Y & Dukler AE. Model for predicting ぼow regime transitions in horizontal and near horizontal gas-liquid ぼow[J]. AIChE Journal, 1976, 22(1): 47-55.

[17] 陈家琅. 石油气液两相管流[M]. 北京: 石油工业出版社,1989.Chen Jialang. Gas-liquid two-phase ぼow[M]. Beijing: Petroleum Industry Press, 1989.

[18] 严谨. 井筒气液两相流动数值模拟研究[D]. 成都: 西南石油学院, 2005.Yan Jin. Numerical study on gas-liquid two-phase ぼow in wellbore[D]. Chengdu: Southwest Petroleum University, 2005.

[19] Brown PP & Lawler DF. Sphere drag and settling velocity revisited[J]. Journal of Environmental Engineering, 2003, 129(3): 222-231.

[20] Clift R & Gauvin WH. Motion of entrained particles in gas streams[J].The Canadian Journal of Chemical Engineering, 2010,49(4): 439-448.

[21] Flemmer RLC & Banks CL. On the drag coefficient of a sphere[J]. Powder Technology, 1986, 48(3): 217-221.

[22] Khan AR & Richardson JF. The resistance to motion of a solid sphere in a fluid[J]. Chemical Engineering Communications,1987, 62(1/6): 135-150.

[23] Haider A & Levenspiel O. Drag coefベcient and terminal velocity of spherical and nonspherical particles[J]. Powder Technology,1989, 58(1): 63-70.

[24] Barati R, Neyshabouri SAAS & Ahmadi G. Development of empirical models with high accuracy for estimation of drag coefベcient of ぼow around a smooth sphere: An evolutionary approach[J]. Powder Technology, 2014, 257(5): 11-19.

[25] 邵明望, 奚传棣. 球形颗粒沉降曳力系数拟合关联式[J].化工设计, 1994(1): 16.Shao Mingwang & Xi Chuandi. The drag coefベcient ベtting correlation settlement of spherical particles[J]. Chemical Engineering Design, 1994(1): 16.

[26] Brauer H, Mewes D. Strömungswiderstand sowie stationärer und instationärer Stoff- und Wärmeübergang an Kugeln[J]. Chemie Ingenieur Technik, 1972, 44(13): 865-868.

[27] 魏纳, 孟英峰, 李悦钦, 刘安琪, 班兴安, 蒋小兰, 等. 天然气井连续携液液滴曳力系数研究[J]. 天然气技术, 2007, 1(6):50-52.Wei Na, MengYingfeng, Li Yueqin, Liu Anqi, Ban Xing'an, Jiang Xiaolan, et al. Research on the liquid droplet's drag coefficient for continuous removal of liquid from gas well[J]. Natural Gas Technology, 2007, 1(6): 50-52.

[28] Liu Z & Reitz RD. An analysis of the distortion and breakup mechanisms of high speed liquid drops[J]. International Journal of Multiphase Flow, 1997, 23(4): 631-650.

[29] Helenbrook BT & Edwards CF. Quasi-steady deformation and drag of uncontaminated liquid drops[J]. International Journal of Multiphase Flow, 2002, 28(10): 1631-1657.

[30] Azzopardi BJ, Piearcey A & Jepson DM. Drop size measurements for annular two-phase ぼow in a 20 mm diameter vertical tube[J].Experiments in Fluids, 1991, 11(2/3): 191-197.

[31] 李厚朴, 边少锋, 钟斌. 地理坐标系计算机代数精密分析理论[M]. 北京: 国防工业出版社, 2015: 146-147.Li Houpu, Bian Shaofeng & Zhong Bin. Computer algebra rigorous analysis theory for geographic coordinate system[M]. Beijing: National Defense Industry Press, 2015: 146-147.

[32] 杨继盛, 刘建仪. 采气实用计算[M].北京: 石油工业出版社,1994: 42-43.Yang Jisheng & Liu Jianyi. Practical calculation of gas production[M]. Beijing: Petroleum Industry Press, 1994: 42-43.

[33] 杜敬国, 蒋建勋, 王臣君. 气井连续携液模型对比研究及新模型的现场验证[J]. 兰州石化职业技术学院学报, 2009, 9(2):9-12.Du Jingguo, Jiang Jianxun & Wang Chenjun. Comparative study of carrying liquid gas model and field experimental verification[J]. Journal of Lanzhou Petrochemical College of Technology,2009, 9(2): 9-12.