架通“结”字桥 数形天堑变通途

师：大家好，很高兴和大家一起学习。张老师今天来上课，是带了礼物来的———魔术表演。喜欢吗？请大家看一段刘谦的魔术。（魔术表演视频：一个拼图，拼成正方形。在表演过程中，刘谦分别增加一个1×1的正方形和一个1×2的长方形，每次增加后，形状和面积都保持不变）神奇吗？（生：神奇）最神奇的是什么？

生1：增加两块后，面积不变。

师：是的，这似乎完全颠覆了我们关于面积的认识，增加两块，面积肯定增加，为什么面积会不变呢？今天这节课，我们有一个重要的任务，就是要破解这个魔术！有没有兴趣？

生（齐）：有兴趣！

师：好的，那学习一个什么内容就能破解这个魔术呢？（出示课题：数与形）数，我们有没有学过？（生：学过）说一说，都学过什么数？（生举例：整数、小数……）形呢？有没有学过？（生举例：长方形、正方形、圆形……）数，我们已经学过；形，我们也学过。大家想一想，为什么还要学习数与形？会要学点什么呢？

生：联系起来学。学习它们之间的关系。

师：说得非常好，以前，我们学数的时候只学数，学形的时候只学形。今天，我们要结合起来学，学习数与形的关系。关于今天的学习，老师提出三个词作为目标：第一个是“认识”，对数与形之间的关系有一点点认识；第二个是“理解”；第三个是“欣赏”。关于数与形的关系，有一位著名的数学家作了非常精辟的论述，我们来看一看。（课件出示图1）请大家一起读一读这句话。（生齐读）我愿意相信，现在大家读这句话没什么特别的感受，老师希望大家能通过这一节课的学习，认识、理解继而欣赏这句话。

师：（出示算式：1=1×1）没问题吧？

生：没问题。

师：（出示算式：1+3=）算一算？

生：4。

師：当然是4，但能不能结合第一个算式，换一个答案？

生2：2×2。

师：了不起！特别有数学的眼光。1=1×1，1+ 3=2×2，非常工整。再看：1+3+5=？

生3：3×3。

师：特别好！再来：1+3+5+7=？

生4：4×4。

师：你计算了没有？（学生有的说计算了，有的说不用计算）我们一起算一下吧。真的是16，4×4，没问题。其实正如有些同学说的，不用计算，规律比较明显。那下一个将是？

生5：1+3+5+7+9=5×5。

师：（出示算式）非常好。继续往下写也很简单，不过这些是数还是形呢？（生：数）是的，是数与数的关系。如果按照这样的方式继续往下写，这节课就不能叫“数与形”了，我们得把数与数的关系与图形联系起来。（出示1+3+5=3×3）我们要把这个算式与图形联系起来，大家想想，1可以用什么表示？

生：一个正方形。一个长方形。一个圆形。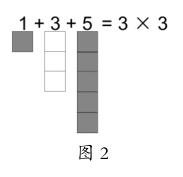

师：都很好，我们就用1个正方形表示1吧。那3呢？（生：3个正方形）5呢？（生：5个正方形）（依次出示1、3、5个正方形，形成如图2所示图形）3×3呢？

生：9个正方形。

师：1是1个正方形，3是3个正方形，5是5个正方形，3×3是9个正方形，这是几年级水平？（生：一年级）是的，我们提高点水平，3×3，别简单地说是9个正方形，行吗？

生6：一个大正方形，有3行，每行3个。

师：是的，这马上就提高到三年级水平了，我们三年级知道了正方形的面积是边长×边长。因此，3×3让我们想起一个边长是3的正方形，它的面积恰好是3×3。（出示图3）请大家仔细观察。左边是1+3+5，对应着那些红色、黄色的正方形，右边是3×3，对应着那个大正方形。通过计算，我们知道，1+3+5=3×3。难不成，左边这些正方形……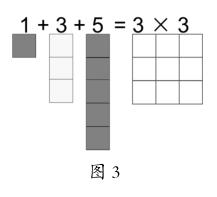

生：和右边一样。

师：是不是呢？左边这些正方形填到右边的大正方形中，是否恰好填满呢？请同学来操作。（一学生操作，形成如图4所示的图形）

师：怎么样？（生：恰好填满）是的！不过稍稍有点遗憾，这个图形不够漂亮。有没有谁来重新摆一摆，把图形变漂亮点？（一学生操作，形成如图5所示的图形）怎么样？（生：漂亮）是的，整齐、漂亮。不过还是有一点小遗憾：1和5不见了！1+3+5，3清清楚楚地在这里，1和5一眼看过去，好像看不见了。有谁可以解决这个问题？（一学生操作，形成如图6所示的图形，学生鼓掌）

师：大家的掌声说明了一切。大家一起看看，1，看到没有？3，看到没有？5呢？3×3呢？（生：看到了）1、3、5很明显，在这，谁来说说3×3在哪？

生7：不看这些颜色，就是3行，每行3个，也就是3×3。

师：你看到没有？（生8：看到了）是的，注意到颜色，很容易看到这是1+3+5。忽略颜色，这就是个3×3的正方形。有首歌是这样唱的———精美的石头会说话。其实，精美的图形也会说话，眼前这个图形，它就在说着1+3+5=3×3，你听懂了吗？说这个图形漂亮，是有理由的。请看。（将3×3的正方形左下角拉开，形成4×4的正方形，如图7）这个图形也在说话，你听懂了吗？

生9：1+3+5+7=4×4。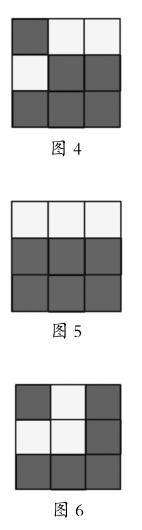

师：1、3、5、7，看到了吗？4×4呢？当然，大屏幕可以继续拉开。（将4×4的正方形左下角拉开，形成5×5的正方形，如图8）有谁知道，此时，我想说什么？（生10：这个图形在说什么话？）真好！是的，听懂了这个图形说的话吗？

生：1+3+5+7+9=5×5。

师：是的，如果我们愿意，可以一下把大屏幕全部拉开。（如图9所示）这个图形又在说什么话呢？同桌互相说说。（学生互相说）请一位同学说说。

生11：1+3+5+7+9+11+13+15+17+19=10×10。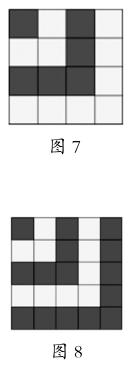

师：是的，这些图形都非常漂亮，大屏幕上的图形呆会就没有了，我们贴一个到黑板上。（贴出图8）还记得它在说什么话吗？（生：1+3+5+7+9=5×5）是的。（从黑板上取下图8）如果没有这个图形，1+3+5+7+9是不是还等于5×5？（生：是的）的确，没有这个图形，这个等式还是成立的。那有了这个图形（再次贴上图8）又有什么不同呢？

生12：更清楚。

生13：一眼就可以看出来。

生14：这个图说明了为什么会相等。

师：是的，还记得华罗庚先生说的第一句话吗？数缺形时少直觉，有了形，数与数之间的关系就变得非常直观了。现在你们有一点认识了吗？我们继续往下看。（出示算式1+2+3+4+5+4+3+2+1）算一算，结果是多少？（生：25）25，会让你想到什么图形吗？

生：一个5×5的正方形。

师：（出示图10）是的，1+2+3+4+5+4+3+2+1恰好等于5×5，难不成，在这个图形里，恰好能找到1、2、3、4、5、4、3、2、1？你看到了吗？看到了的话，和你的同桌互相说说，看是不是英雄所见略同。

生：斜着看。（师演示，最终形成如图11所示的图形）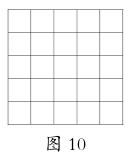

师：漂亮吗？（生：漂亮）是的，说它漂亮，还有一个理由，和前面一样，大幕是可以拉开的。（出示图12）这个图形在说什么话呢？

生：1+2+3+4+5+6+5+4+3+2+1=6×6。

师：是的，大屏幕可以拉开，当然就可以关起。（出示图13）我想大家一定能听懂它说的话。如果愿意的话，我们可以这样。（出示图14）它在说什么话？能听懂吗？

生：1+2+…+10+9+…+2+1=10×10。

师：那相加呢？在分数中，是相加，那在圖形中，又如何表示呢？

生：将图形拼起来。

师：好！是不是只有正方形可以表示1呢？

生：还可以是长方形、圆形。

师：好，这些都是考虑面积，是不是只能考虑面积？

生15：还可以用线段的长度表示！

生19：更加容易理解，更直观。

师：是的。因此，华罗庚先生说“数缺形时少直觉”。还记得课前说过，我们这节课还有一个重要的任务吗？（生：破解刘谦的魔术）是的，现在是时候了。不过，刘谦先生是职业魔术表演艺术家，破解他的魔术，有点不厚道。这样吧，我们来破解一个与他的魔术类似的魔术。（动画演示，一个三角形被分成 4块，不同的拼法，结果不同，如图16所示）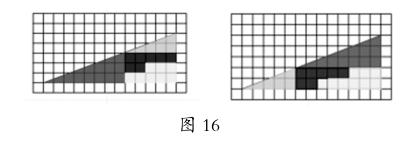

师：想了解这是为什么吗？那你得再打起精神，听我讲3分钟你以前从没听说过的数学。（借助图17，介绍角的大小可以由一个分数表示）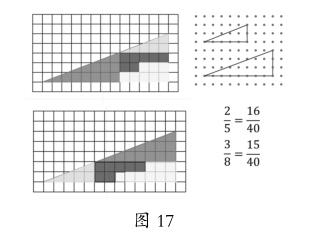

师：我们可以看出，这两个角的大小并不相等，我们的拼法是有问题的，只是因为区别很微小，光看图形，我们是看不出来的。真要知道这里的细微区别，必须靠什么呢？

生：必须靠计算。

师：是的，要靠数，靠数的运算。所以，华罗庚先生才说“形少数时难入微”。以后，我们看到刘谦的魔术，一方面是欣赏，另一方面也要做到心中有数。如何？对数与形之间的关系，以及华罗庚先生对这种关系的精辟描述，有没有一点欣赏？现在，请大家把华罗庚先生的这句话齐读一遍。老师希望大家在读第一句时，注意到黑板上的两个图形，在读第二句时，注意到那个魔术。（生齐读）好，今天的课就上到这里，下课。

（作者单位：长沙市教育科学研究院）

点评

“数与形”一课，张老师曾经上过，本刊在2016年第2期刊登了。去年11月，张老师在湘乡市又展示了本课的改进版，笔者在现场听完后感慨：常教常新，堪称经典。思考月余，再向张老师约稿重发，并将自己的思考写出来，以飨读者。

数学史上，数与形要结合，可谓筚路蓝缕。真正结合起来是笛卡尔坐标系的建立，距今也只有400余年历史，足见结合不是那么容易的。

那么，今天要教学生数形结合，老师要怀有敬畏历史之心，研究学生学习之情，思考教给学生之法，在“结”字上下巧功夫，才能上出赢得学生掌声的课。

张老师精读数学史，熟谙学生学习数学的心理，长于娓娓道来、寓神奇于平凡之中的谈话教学之法，将数与形这么高深的一课上成了经典。笔者循着张老师上课的轨迹，带领大家一路欣赏。

你看课始，张老师问学生：知道数、形吗？学生都能举例对答。可见，学生对数、形已经熟练，无须多言。那么，数与形要结合，如何“结”？老师要做的事情就是架好“结”这个桥，才能使天各一方的数、形连在一起。

往下看，张老师架桥啦。先从单个数用形表示开始，这不难。话锋一转，算式1+3+5如何用图形表示呢？这是本课的难点所在！学生说出结果是9，张老师用风趣的语言评价：“这是一年级水平。”话很轻松，却很能引发学生的思考：怎么表示就能提高水平呀？3×3！“这马上就提高到三年级水平了，我们三年级知道了正方形的面积是边长×边长”。这样就将1+3+5与正方形联系起来了，也就有了桥的雏形，接下来要做的是装饰桥，使桥漂亮、美观。

学生将散落的9个正方形摆到3×3的正方形中，前面的两种摆法（如图1所示）张老师都不那么满意，“有稍稍的遗憾”。当稍微调整一下变为第三个图（如图2）时，课堂立即响起了掌声。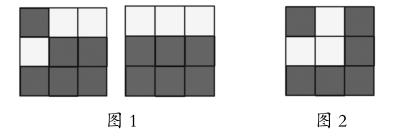

老师们，这掌声是学生真正发自内心的赞叹，也是学生对1+3+5用第三个图形表示得如此完美的心领神会的表白。我们在平时听课的过程中也发现有学生鼓掌，但那是学生被动鼓掌，因为都是执教老师（包括很多所谓的名师）要求的。

至此，老師们请闭目微思，数与形的神韵是不是在“结”？

好的开头是成功的一半，后一半同样是好戏连台。申老师继续领着大家领略后一半的精彩。

一座桥架好了，就要发挥桥的作用了。

1+3+5+7，1+3+5+7+9，……用图形来表示，学生就不需要另起炉灶了。张老师凭借娴熟的计算机技术，设计了非常精巧的课件。只要将上面第三个图形拉开，就能得到所想要的图形，真是“一图在手，数形毕露”。

“形缺数时难入微”。这样的例子在小学范围内是很难找的。张老师用数学的眼光观察刘谦魔术并将这一素材很好地运用在教学中。对这个魔术要解释清楚，必须用到初中的三角函数知识。张老师讲三角函数定义时灵活处理，说成直角三角形中两条线段的比，比较接近学生的认知水平了。小学生能有个模糊的认识就可以了。

申老师领着大家欣赏了张老师的课，说了这么多了，不知说清楚没有。老师们如果还有不明白的地方，请多读一遍课堂实录，对照自己的教学过程进行思考，应该会明白张老师课的神韵。谢谢大家的阅读。