基于CFD的半削平基础平台对风电机组的影响研究*

文 | 付炳瑞，王海斌，胡威

在风电场基础建设过程中，为了节省成本，减少挖平台的土方量，经常将山头挖至可以浇筑风电机组基础时就停止施工，在风电机组基础旁留下10m－20m高未削去的半个山头，机位微地形的改变对前期风资源评估会有一定的偏差，从而对机组运行安全造成隐患。本文将以山西某风电场为例，利用机组SCADA实测数据和CFD流体仿真手段，研究上述微地形的改变对轮毂高度处湍流和机组振动的影响。

山西某风电场项目背景

山西某风电场共吊装29台机组，2014年年底完成调试并网运行，运行过程中部分机组出现机舱加速度超限故障，其中大部分机组存在基础平台半削平的情况。

SCADA数据分析

本文选用机组运行的SCADA数据，时间长度为2015年1月1日到2015年12月31日，选取场区内A、B两台典型故障机组和C、D两台正常机组，四台机组所处的地形情况如图1所示。故障机组与正常机组所处的地形相似，A机组和C机组与B机组和D机组各位于一道山梁，大地形下环境大体相同，因此对于研究微地形的影响具有较好的参考性。

通过处理机组SCADA数据，本文将从湍流标准偏差、阵风因子、机舱加速度有效值和功率曲线四个方面讨论机组局地风资源情况和运行状态。

一、湍流标准偏差分析

通过分析问题机组的故障文件可知，该项目机组发生机舱加速度超限故障的时间段主要集中在四月和十二月，即春冬季节，一年中风速最大的月份也恰好在四月和十二月。

图1 四台机组所处的地形情况

在北方春冬季节，植被稀疏，影响机位处湍流的因素以地形为主。湍流标准偏差是衡量10min样本内数据强弱的量度，反映数据的脉动程度，用公式（1）表示：

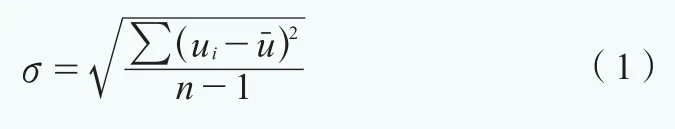
其中ui为瞬时风速，u为样本平均风速，n为样本内数据个数。

在正常湍流模型中，湍流标准偏差代表值σ1应为轮毂高度处风速的90%，对于标准风力发电机等级，这个值由式（2）给出：

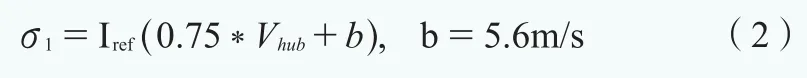
将实测数据计算湍流标准偏差值与代表值曲线进行对比，来验证实际湍流特征与IEC标准适应性。以2015年4月为例，A和B机组湍流标准偏差随时间的变化如图3（a）和（b）所示。从图中可知机位湍流标准偏差在大于10m/s的风速段内有较多的数据点，超出IEC标准规定的正常湍流模型中A类湍流标准偏差曲线，且这些数据点在风速维度上分布较为分散。反观C和D正常运行的机组，其湍流标准偏差随时间的变化如图3（c）和（d）所示，机位湍流标准偏差在大于10m/s的风速段内的数据点超出在IEC标准规定的正常范围。模型中超出A类湍流标准偏差曲线的数据点较少，且这些数据点在风速维度上相对集中，均在风速18m/s左右分布。四台机组湍流标准偏差与IEC标准值的对比见表1，从表中可知，四台机组实测湍流标准偏差在IEC湍流标准偏差A类代表值曲线以下的涵盖比均超过90%，但A和B两台故障机组实测湍流标准偏差在IEC湍流标准偏差B类代表值曲线以下的占比却低于90%。

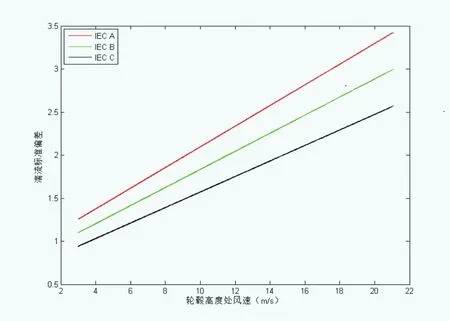
图2 正常湍流模型（NTM）的湍流标准偏差

表1 2015年4月四台风电机组湍流标准偏差与IEC标准值对比

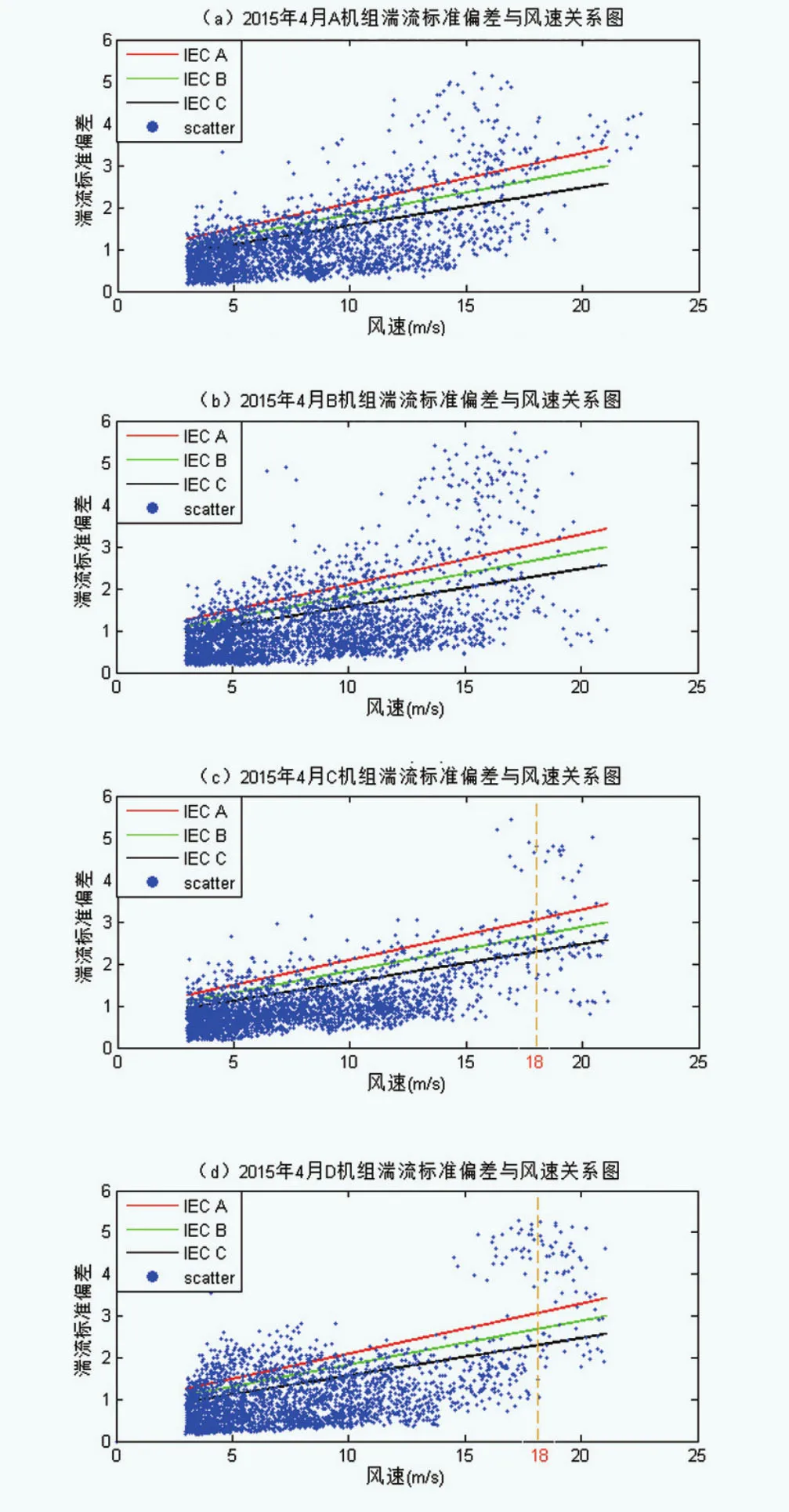
图3 2015年4月四台机组湍流标准偏差与风速关系图

二、机舱加速度有效值分析

2015年4月1日，A和B机组因发生机舱加速度超限故障，两台故障机组当天的机舱加速度有效值如图4（a）和（b）所示。由图可知两台机组在部分时段内机舱加速度有效值超过0.1g，甚至达到0.16g，触发机舱加速度超限故障的最低条件。然而同一时段内这两台故障机组附近的C和D机组运行正常，其机舱加速度有效值见图4（c）和（d），C和D机组机舱加速度有效值均未超过0.1g。

三、阵风因子分析

通常定义阵风因子为阵风持续期tg内平均脉动风速的最大值与基本时段内的平均风速之比，即：

2015年4月1日四台机组阵风因子随时间变化的散点图如图5所示，从图中可知A和B故障机组的阵风因子存在超过2的时段，而且这一时段恰好与故障发生时间相吻合；而在同一时间段内，C和D机组阵风因子均未超过2。经统计风电机组实测数据样本中阵风因子超过1.4的频率见表2，由表可知，A和B故障机组阵风因子超过1.4的频率占比均超过10%，且日平均阵风因子偏大。

表2 风电机组实测数据样本中阵风因子超过1.4的频率统计

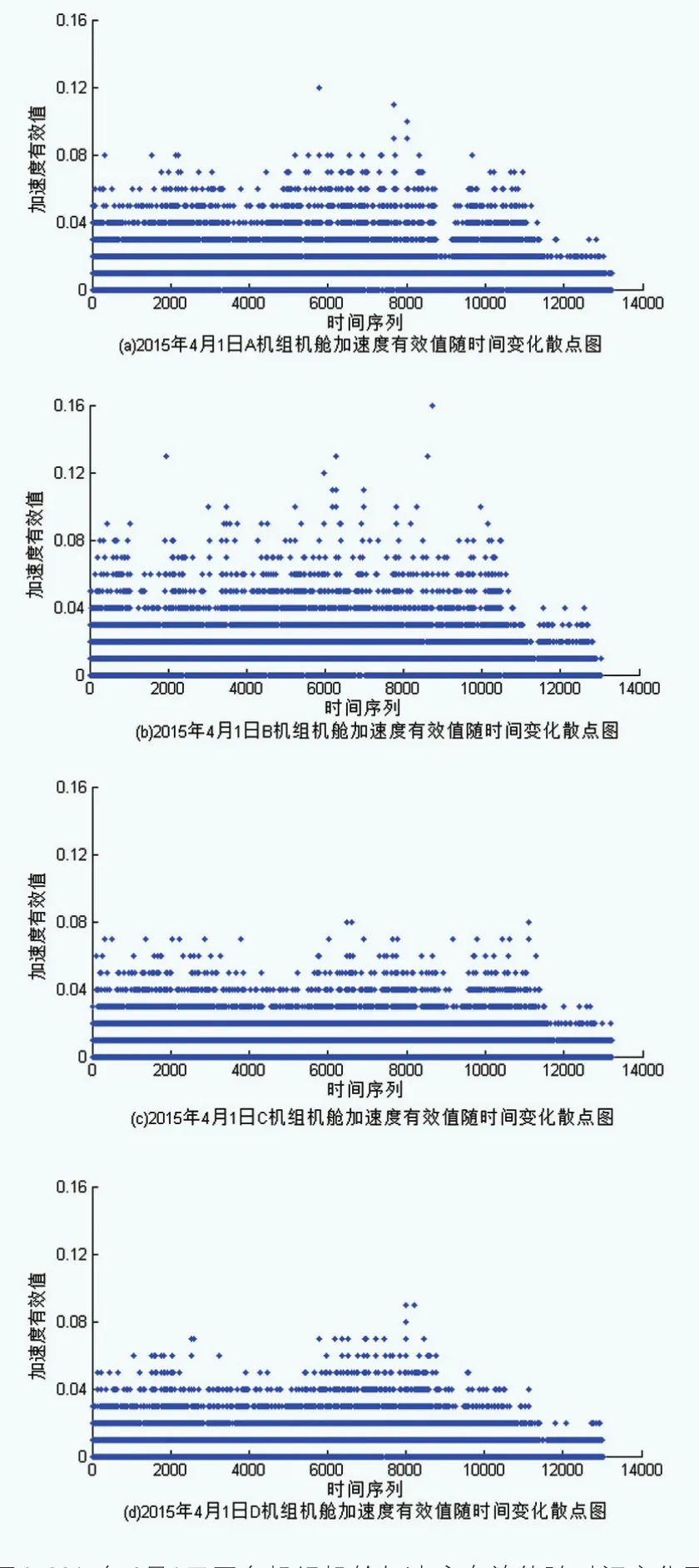
图4 2015年4月1日四台机组机舱加速度有效值随时间变化图

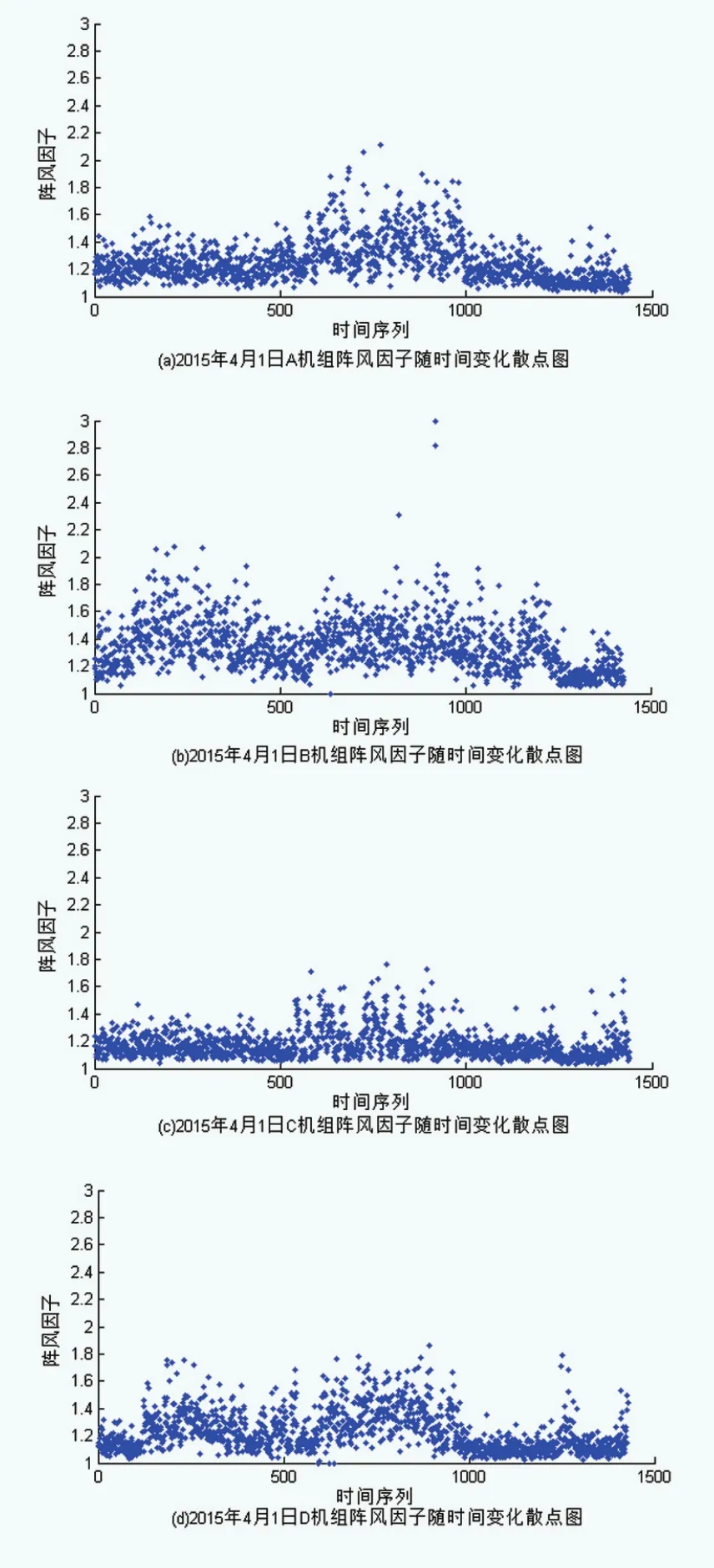
图5 2014年4日1日四台机组阵风因子随时间变化散点图

四、故障机组对功率曲线的影响

故障机组不仅在湍流标准偏差、机舱加速度、阵风因子等方面存在异常，而且对功率输出方面也有较大的影响，其功率曲线如图6所示，2015年4月A和B机组的功率曲线在额定风速段内出现较大幅度的下降。

五、故障机组地形分析

从现场地形分析，距离A机位的东侧约22m处有一高约10m的半削平山包，同样在距离B机位的东部约20m也有一高约11m的半削平山包，两台机组所处的地形相似。另外，两台机组与测风塔的相关性较好（见图7），说明测风塔对这两台机组有一定的代表性，因此用测风塔数据进行分析是可行的。

经分析2015年4月1日测风塔的风向为东偏东南，由此可知两台机组旁边的半削平山头恰好位于机组的主风向。机组叶片最底端距离地面约30m，其与附近的半削平山头在垂直高度上有不足20m的高差，当风从山头一侧吹向风电机组时，气流受到阻挡而发生畸变分离，不仅产生较大的湍流，而且导致风速沿塔筒高度方向变化很大。

借助机组SCADA数据，只能监测轮毂高度处来流变化情况，而无法获知其他高度层的风参数以及流场变化。为了更好地解释半削平山头对下风向风电机组的影响作用，下文将采用CFD流体模拟仿真技术对场区地形进行流场模拟。

图6 2015年4月A和B机组网侧有功功率与标准功率曲线的对比

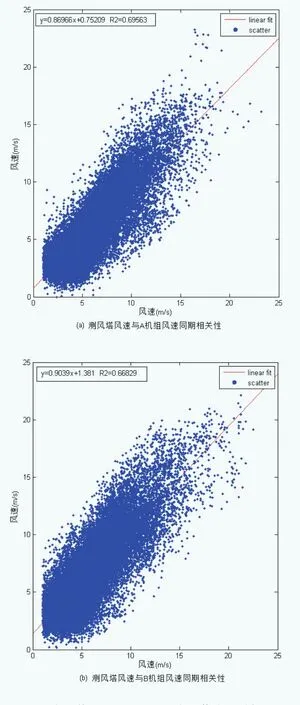
图7 测风塔与A和B机组风速同期相关性验证

CFD模拟仿真

CFD模拟仿真技术可较好地应用于风电场复杂地形的流动模拟, 再现复杂地形的大气边界层内的流动。为了更加直观地描述气流流经半削平山头后的流场变化情况，本文首先对半削平山头实现3D建模，然后采用流场仿真模型对半削平山头的流场进行仿真模拟，最后从机组平台的垂直剖面和水平剖面分析半削平平台对机组的影响。

图8展示了模拟方案设置及数据传递流程。半削平处的小山包与机位点平台的海拔相差10m，模拟区域设置网格分辨率为1m×1m×1m，提取测风塔风速、风向、气温、湿度数据生成边界廓线作为模拟区域的初始条件，对半削平风电机组平台处的流场进行模拟。

一、垂直剖面模拟分析

假设平台处高度为0m，根据前述方法模拟半削平风电机组平台垂直方向上0m－80m各高度处的环境湍流变化情况，具体模拟结果见图9和表3。

根据CFD流体模拟仿真结果，风电机组平台处的湍流强度在半削平小山包的10m高度附近达到最大，随着高度的上升，环境湍流值逐渐减小，且环境湍流值在30m高度处有较大的变化，该结论与障碍物对湍流的影响结论一致，即受障碍物的影响，涡流扰动区的影响高度范围约为障碍物高度的3倍。风电机组叶片扫风最低点所处的高度一般距地约为20m－30m，若气流从半削平风电机组平台处的小山包流经下风向的风电机组平台会发生气流分离，山包与平台间的海拔差越大，则气流分离就越严重，影响的叶片扫风面的面积越大，进而给叶片的受力、机组的载荷带来一定影响，最终影响机组正常发电。

二、水平剖面模拟分析

假设半削平的小山包与机位点平台处海拔相差10m，如图10所示，在水平剖面上（其高度与平台高度一致），由于受半削平平台的影响，半削平的小山包对风有阻挡作用，在小山包前后均形成回流区，对机组的发电量和载荷安全产生影响。

三、半削平风电机组平台对环境湍流的影响分析

原山头处垂直剖面上环境湍流见图11，半削平风电机组平台垂直剖面上环境湍流见表4。

由表4可知，从原山头与半削平风电机组平台环境湍流值变化情况来看，环境湍流值突变的高度层发生在风与地表接触的那一层高度，即山地地形中贴近地表处的湍流值最大，贴近地表处的湍流对机组有一定的影响，从而增加机组振动的可能性。

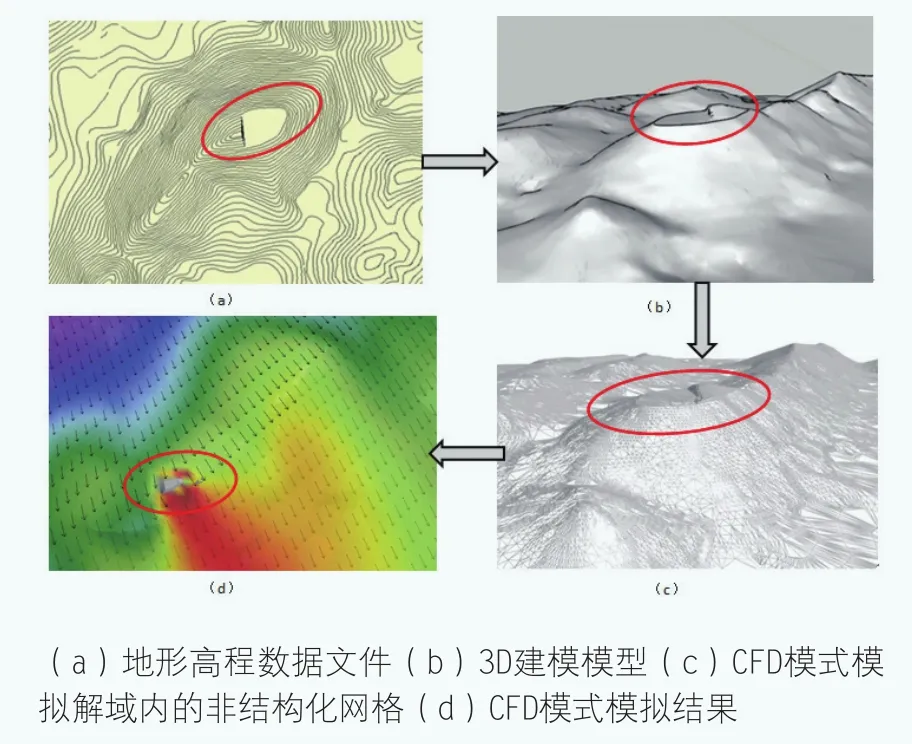
图8 地形模拟仿真流程

图9 半削平风电机组平台垂直剖面上环境湍流

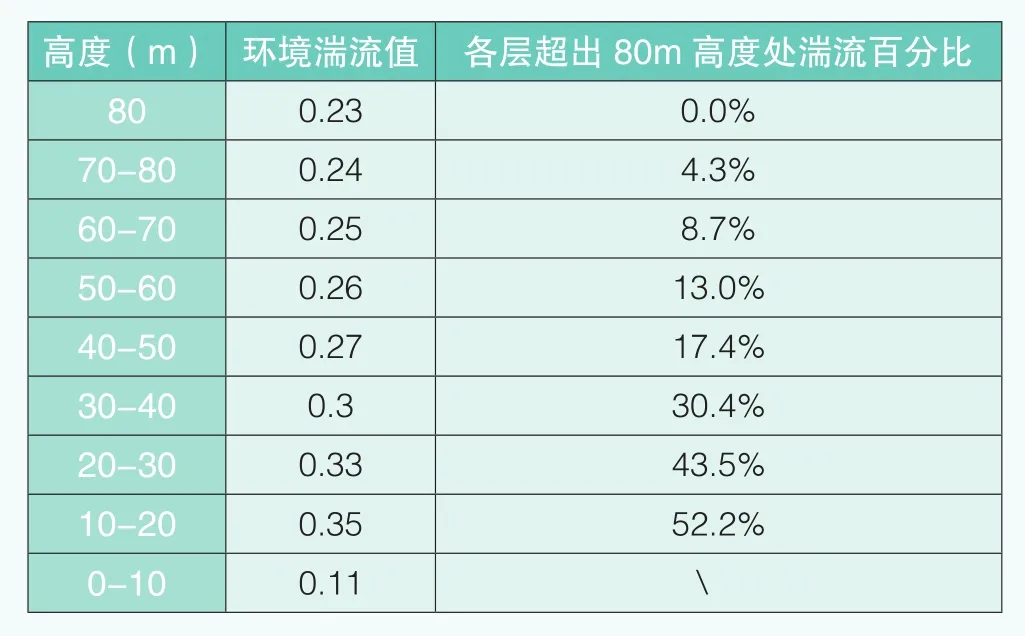
表3 半削平风电机组平台垂直方向上0m-80m处的环境湍流变化情况

图10 半削平风电机组平台水平剖面上环境湍流情况（风流场平面高度与平台高度一致）

图11 原来山头处垂直剖面上环境湍流

结论与建议

通过对机组SCADA数据和CFD仿真模拟的分析，位于机组上风向的半削平山头前后形成较大湍流的回流区，特别容易对机组下旋叶片的气流造成扰动。从发电量角度来看，气流扰动会影响叶片正常变桨，使其无法达到理论最优Cp值，最终导致机组出力较差，发电量降低；从机组载荷适应性角度来看，气流扰动会引起机组振动、叶片寿命减少等问题。风速越大，气流流经半削平山头产生的脱流效应会更加强烈，最终会导致机组机舱加速度超限故障。

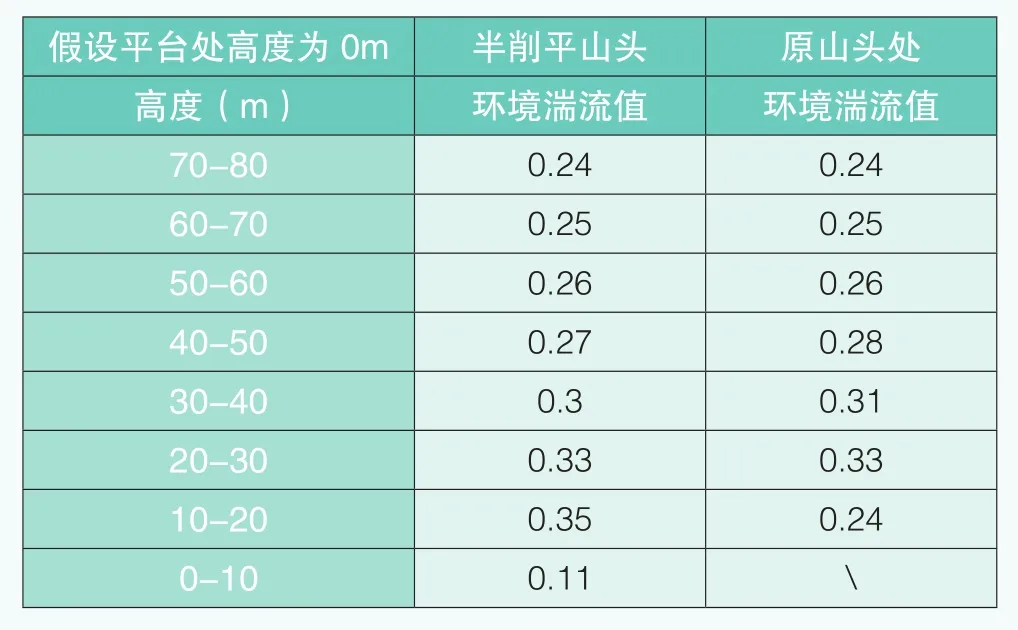
表4 半削平山头与原山头处环境湍流对比

建议在今后的风电场建设中，尽量保证机组平台周边平整，避免半削平山头情况出现，虽然在前期投入成本增加，但在后期风电场运维和发电量收益中，可以减少不必要的损失。

摄影：黄斌