加减速时地铁列车隧道气动性能研究

刘冬雪，蒋雅男，杨明智



加减速时地铁列车隧道气动性能研究

刘冬雪1, 2，蒋雅男3，杨明智1, 2

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 轨道交通安全教育部重点实验室，湖南 长沙 410075；3. 中铁第六勘察设计院集团有限公司，天津 300308)

采用三维、可压缩、非定常-方程的数值计算方法，研究A型地铁列车在隧道内加减速时车体表面压力变化和车内压力变化，分析隧道净空面积与密封指数的关系，并采用动模型实验验证数值计算准确性。研究结果表明：列车在隧道内运行时，随着阻塞比的减小，测点压力幅值随之减小，主要体现在对正峰值的影响，压力变化规律基本一致；阻塞比越小，列车表面压力幅值随列车长度方向的变化趋势越平缓；列车以匀速、减速和加速3种方式运行，隧道断面为22 m2时，根据美国标准列车气密性需分别大于6，3和6 s，根据国内标准需分别大于10，6和10 s；隧道净空面积小于35 m2时，根据美国标准列车气密性需分别大于2，0.7和1.5 s，根据国内标准需分别大于3，0.4和1.5 s。

地铁；数值模拟；动模型实验；加减速；气动效应；阻塞比

随着经济、社会快速发展，城市交通运输日趋紧张。作为解决交通拥堵、居民出行困难的有效途径，地铁在现代交通中已占据重要位置[1]。地铁列车具有运行间隔短、频繁启停的特点[2]，加减速对地铁列车运行具有重要的影响，因此有必要研究加减速时地铁列车的隧道气动效应。国内外学者对列车隧道空气动力效应均有所研究。MA等[3]研究了高速列车在隧道口处微气压波的影响因素和变化规律。Rabani等[4]模拟了隧道截面积突变对压力波及阻力的影响。Chu等[5−6]对两列车在隧道中交会时引起的三维流动进行了模拟。Kim等[7]利用锐化接口动网格方法，计算了地铁列车地铁隧道内压力变化。Marta等[8]利用动网格技术研究了具有纵向通风系统的地铁隧道的活塞效应问题。梅元贵等[9−10]对高速铁路初始压缩波、列车通过隧道及隧道内会车压力波进行了数值分析。林世生等[11−12]研究了地铁列车空气动力效应。李志伟等[13−16]在列车通过隧道数值算法及其应用方面进行了深入研究。地铁在隧道内运行时所产生的压力及压力变化率如若超出某个界限，轻则会出现司乘人员耳部不适，舒适性降低，重则造成乘客失聪。因此应对隧道内的压力及压力变化率做出一定限制。我国标准均属于铁路标准，地铁列车舒适性标准尚无依据可循。本文结合地铁列车自身的运行特点，对地铁隧道内空气动力学效应问题进行了三维模拟。得到了地铁列车分别以匀速进出隧道、隧道内减速到达站台和加速驶离站台等三种运行场景通过隧道时，隧道阻塞比与隧道内压力波及压力变化率的关系，获得了隧道净空面积与密封指数的关系。

1 数学模型

列车在隧道内运行时，隧道内空气由于隧道壁面和车体表面的限制而受到强烈挤压，因此必须将空气视为可压缩的理想气体。列车周围流场的雷诺数约为106级，列车周围流场为湍流状态。因此，采用三维、可压、非定常-方程来求解。

计算采用CFD软件—Fluent，压力速度修正采用SIMPLEC算法，对流项采用高阶精度的SECOND格式离散，扩散项采用二阶中心格式离散[17]。

2 计算模型、区域及边界条件

2.1 计算模型

本文采用6车编组的地铁A型列车为计算模型。在不影响计算结果的前提下，对列车外形进行了简化，同时忽略了转向架的影响。计算模型如图1(a)所示，列车模型高为3.8 m，宽为3 m，整车长为139.5 m，列车横截面积为9.785 m2。根据现有地铁隧道情况，隧道模型断面如图1(b)所示。净空面积为22 m2，地铁A型车与隧道截面的阻塞比为0.445。为尽可能保持计算结果的真实性，在隧道中间位置设置地铁车站模型，如图1(c)所示。车站前后的盾构井尺寸为12.9 m×9.5 m×6.585 m，站台尺寸为237 m×3.9 m×4.55 m。

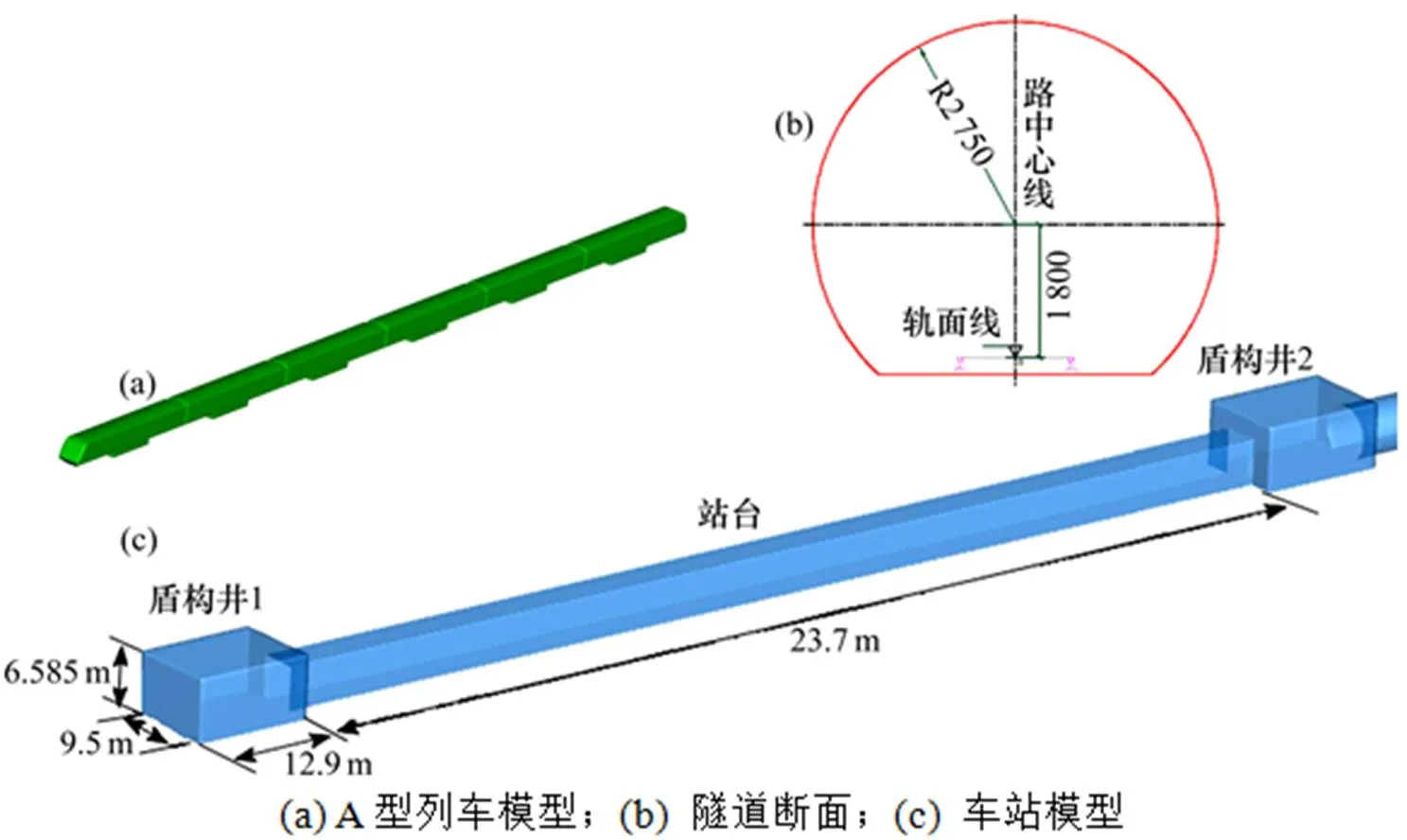
图1 计算模型

2.2 计算域及边界条件

为模拟地铁列车过隧道问题，采用对流场进行分区对接滑移网格技术，即在有相对运动的不同网格间设置公共滑移界面，从而实现彼此的数据交换。在计算地铁列车分别以匀速、减速和加速等3种运行方式在隧道内运行时，结合地铁隧道的工程特点，采用了3种不同的计算区域模型，如图2 所示。

图2 计算区域

如图2，对于列车表面，给定运动边界条件：方向速度分量为给定的列车运行速度，和向速度分量等于0。流域两侧面、顶面、底面及隧道壁面、地面均给定无滑移边界条件。出口给定压力出口边界条件，相对压强为0；进口给定压力进口边界条件，相对压强为0。由于地铁隧道较长，在研究地铁列车在隧道内减速运行和加速运行时，隧道入口/出口相反的一侧采用远场边界即无反射波返回(图2(b)和2(c)所示)。

3 动模型实验

为验证本文数值计算结果的正确性、可信度及是否达到工程计算所需精度，利用由中南大学轨道交通安全教育部重点实验室的动模型试验装置，对地铁列车以不同速度通过隧道进行了动模型试验，并进行了相同工况的数值模拟计算。

此次模型试验采用1:20的缩比模型，图3(a)为地铁列车单车过隧道时，隧道壁面上的测点布置示意图，隧道壁面上共布置15个测点，图3(b)给出了地铁列车车体表面测点布置示意图，共布置18个测点。

表为地铁列车以100 km/h通过6 m直径隧道时，列车表面和隧道表面测点瞬变压力变化与动模型试验结果对比，图4为列车表面和隧道表面测点压力变化曲线对比图。

图3 模型测点布置图

表1 动模型实验结果与计算结果比较

图4 测点压力变化曲线

由以上结果可见，数值计算所得到的流场压力变化曲线与动模型试实验规律基本一致，幅值相对误差在5%之内，说明本文采用的数值计算方法可以较好地模拟地铁列车在隧道内运行时所引发的空气动力效应问题。

4 计算结果分析

4.1 地铁列车隧道气动性能

4.1.1 地铁列车匀速通过隧道

图5(a)和5(b)为不同阻塞比下0.445，0.391，0.349等3种工况下，第3节车厢中部测点及距隧道入口500 m处隧道壁面测点压力变化曲线。从图7中可以看出，随着阻塞比的减小，列车表面测点及隧道壁面测点压力也随着减小，但压力变化规律基本一致。阻塞比从0.445降至0.391时，列车表面测点正峰值降幅为26.02%，负峰值降幅为5.53%，隧道壁面测点正峰值降幅为22.16%，负峰值降幅为6.7%；而阻塞比从0.391降至0.349时，列车表面测点正峰值降幅为24.03%，负峰值降幅为11.25%，隧道壁面测点正峰值降幅为18.97%，负峰值降幅为11.77%。阻塞比对正峰值的影响比对负峰值的影响大。

图5 不同阻塞比下测点压力变化曲线

图6为不同阻塞比时列车表面测点及隧道壁面测点压力幅值沿长度方向的变化规律。从图6中可以看出，随着阻塞比的减小，列车表面测点及隧道壁面测点压力幅值也随着减小，阻塞比越小，列车表面测点压力幅值随列车长度方向的变化趋势越平缓。不同阻塞比时，测点压力幅值沿长度方向变化规律基本一致，列车表面测点幅值从头车向尾车逐渐降低，隧道壁面测点压力幅值在距隧道入口350 m处达到最大值，最大幅值分别为6.29，5.11，4.37，3.95和3.16 kPa。当阻塞比由0.445降至0.279时，列车表面压力幅值最大降幅约为46.87%，隧道壁面压力幅值最大降幅约为54.43%。

图6 不同阻塞比下测点压力幅值变化曲线

4.1.2 列车隧道内减速到达站台

图7为阻塞比分别为0.445，0.391和0.349时，第一节车厢中部测点与距隧道入口200 m处测点压力变化曲线。从图中可以看出，阻塞比不同时各测点的压力变化规律一致。当阻塞比由0.445降至0.349时，车体表面测点压力幅值降幅为39.19%，其中正峰值降幅为46.67%；隧道壁面测点降幅为33.45%，其中正峰值降幅为38.08%。可以看出，列车隧道内减速运行时，阻塞比对测点压力幅值的影响主要源于对正峰值的影响。

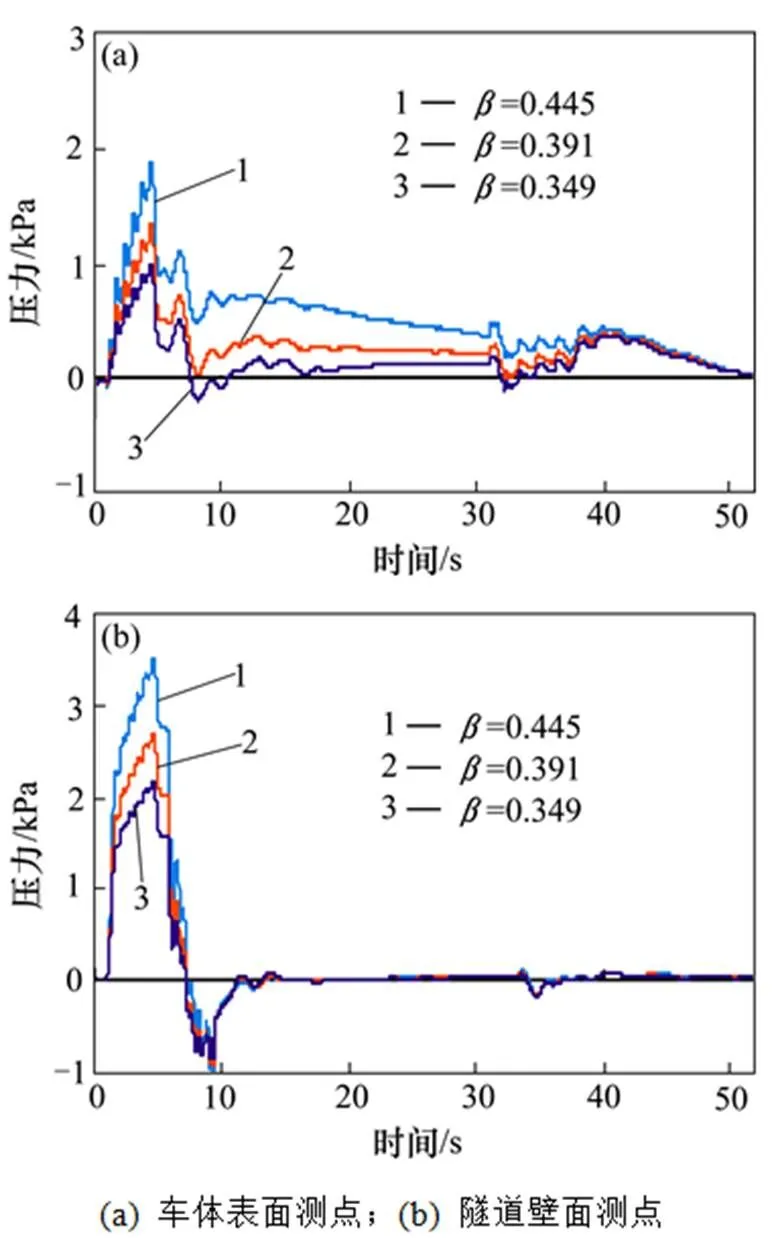
图7 不同阻塞比下测点压力变化曲线

图8为列车以相同初始速度在不同阻塞比隧道内减速运行时，测点压力幅值沿长度方向变化趋势。由图中可以看出，随着阻塞比的减小，测点压力幅值亦随着降低。阻塞比越小，列车表面测点压力幅值从车头向车尾方向的变化趋势越平缓，当阻塞比减小到0.279时几乎呈一条直线；隧道壁面测点压力幅值沿长度方向变化趋势基本一致，在距隧道入口250 m及500 m处存在2个极值点，在距250 m处达到最大值。阻塞比由0.445减小到0.279时，列车表面测点压力峰峰值最大降幅为61.73%；隧道壁面测点压力峰峰值最大降幅为54.69%。

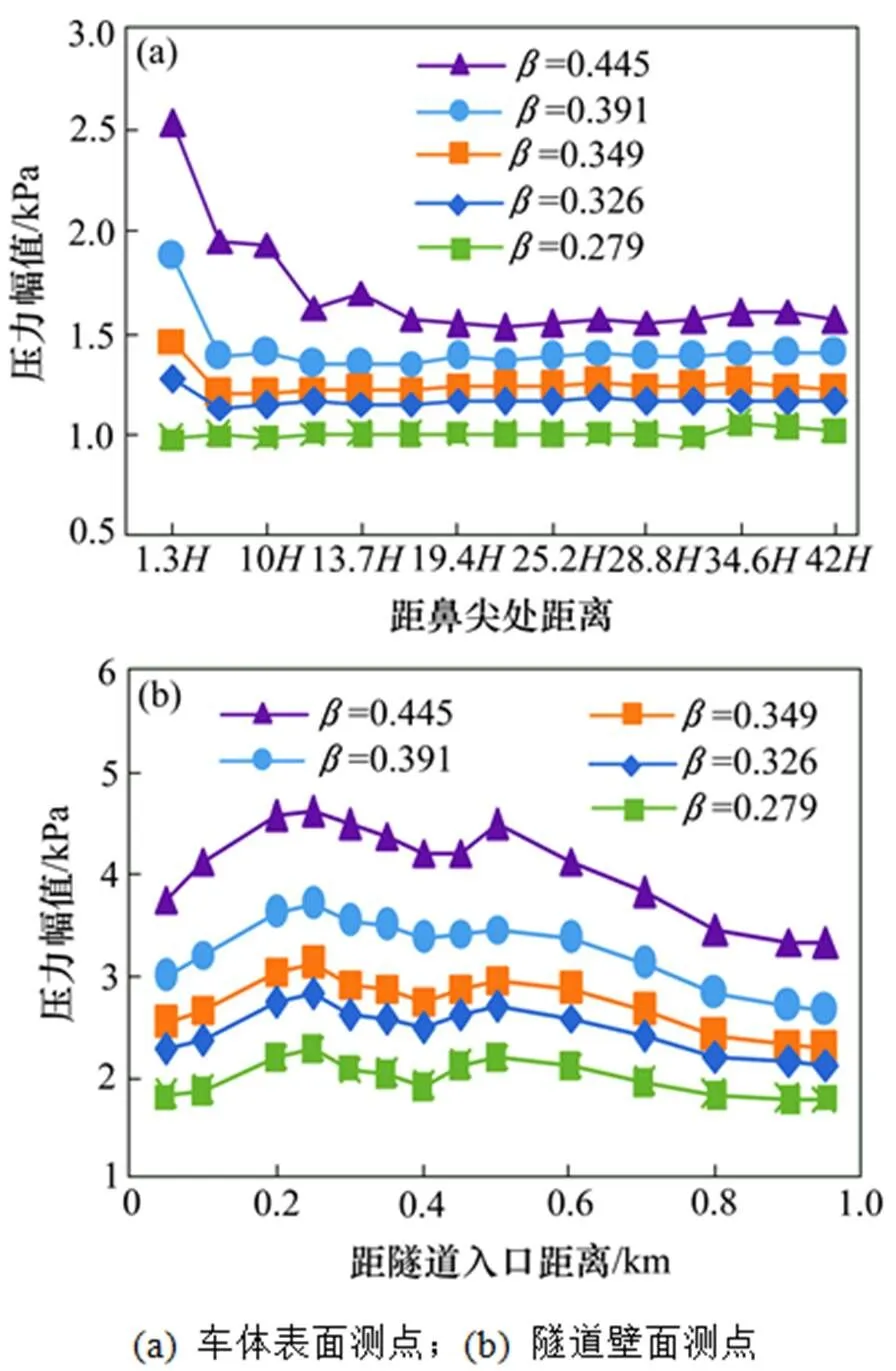
图8 不同阻塞比下测点压力幅值变化曲线

4.1.3 列车隧道内加速通过站台

图9(a)和9(b)为列车以140 km/h最高时速通过阻塞比分别为0.445，0.391和0.349隧道时，第四节车厢车体中部表面测点及距站台出口500 m处测点压力变化曲线。由压力曲线图可以看出，不同阻塞比时，测点的压力变化趋势基本相同，当阻塞比由0.445降至0.349时，列车表面测点负峰值由2.35 kPa升至1.64 kPa，降幅30%；隧道壁面测点负峰值由2.42 kPa升至1.35 kPa，降幅44%。可以看出，列车隧道内加速运行时，阻塞比对测点压力幅值的影响主要源于对正峰值的影响。

图10为列车加速通过不同阻塞比隧道时，列车表面及隧道壁面测点压力幅值沿长度方向变化趋势。从图11可以看出，不同阻塞比下，列车表面测点沿车长方向的变化趋势及隧道壁面测点沿隧道长度方向的变化趋势基本一致。列车表面测点由头车向尾车压力幅值呈上升趋势；阻塞比越小，变化趋势越平缓。隧道壁面测点均在距站台出口800 m处达到最大值。随着阻塞比的减小测点压力幅值随之降低，当阻塞比由0.445降至0.279时，列车表面测点压力幅值最大降幅为40.65%，隧道壁面测点压力幅值最大降幅为40.53%。

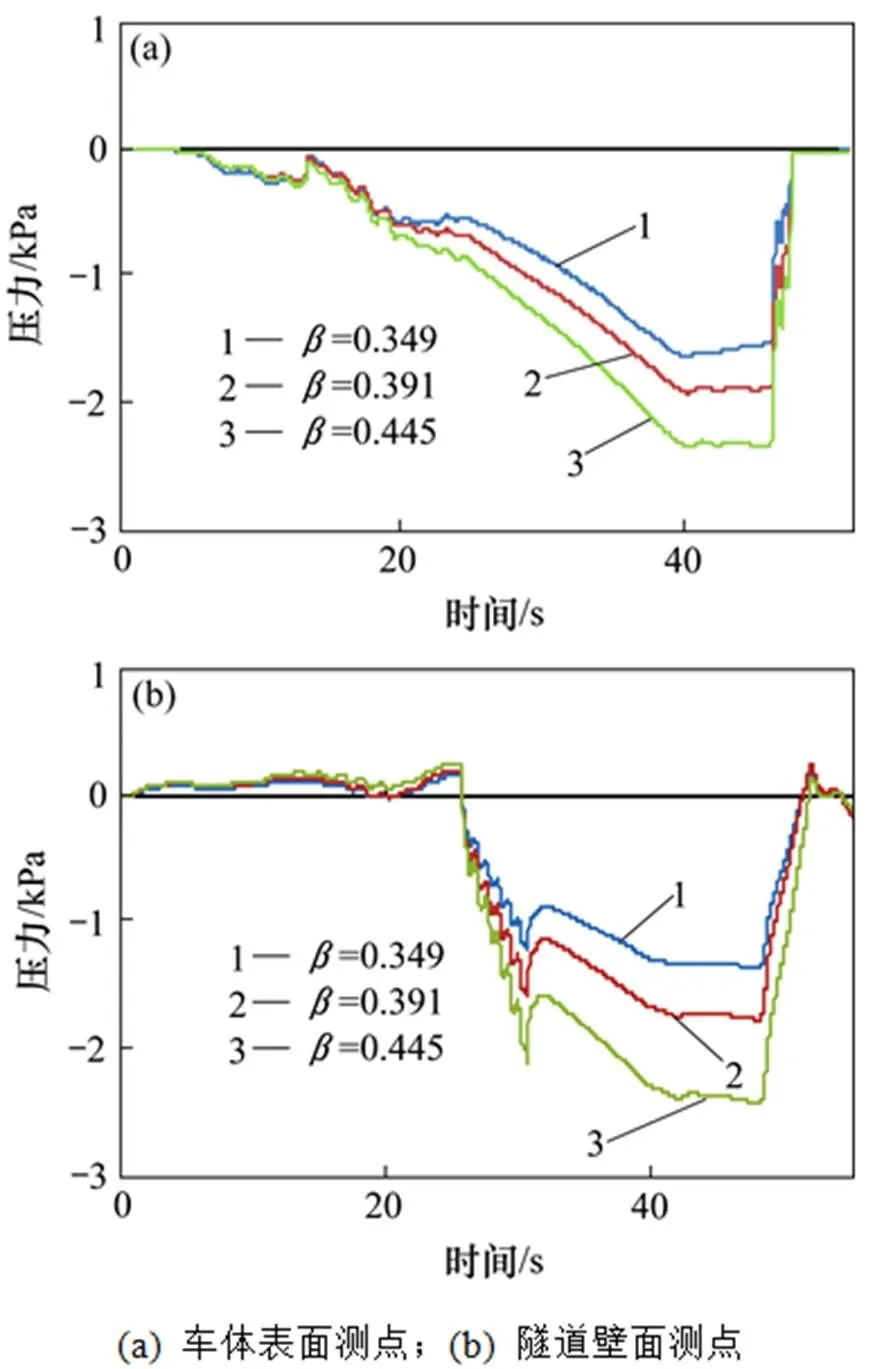
图9 不同阻塞比下测点压力变化曲线

4.2 合理净空面积的选择

通过数值计算可以得到车体表面任意一点的变化压力，然后根据车体表面压力变化求出车厢内部的压力变化，车外的压力向车厢内部传播主要取决于车体的刚度和车辆的气密性。列车的刚度比较大，可以忽略其影响。因此，本文主要考虑车辆的气密性的影响。

假定车内压力变化率与内外压差成正比：

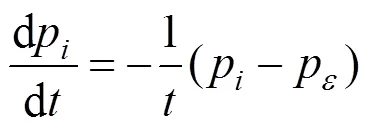
式中：p为车内部压力；p为外部压力；为密封指数。由气密性试验测量得到：

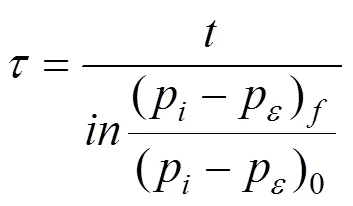
根据式(2)，由列车车体表面的压力变化，计算得到车厢内部的压力变化率，进而得到隧道净空面积A与密封指数的关系。

图10 不同阻塞比下测点压力幅值变化曲线

图11~13分别为列车以最高时速140 km/h匀速通过隧道、减速到达车站、加速驶离车站时，不同列车密封指数(取=0.4，0.7，1.5，2，3，6和10 s)下，最大车内压力变化率与阻塞比的关系曲线。其中标准限值分别为美国地铁标准([]<700 Pa/1.7 s；P<410 Pa)及国内标准([]<800 Pa/3 s)。

列车以140 km/h匀速通过隧道时由以上计算结果可以得出，根据美国地铁标准，若在现有地铁隧道断面(A=22 m2)情况下，将列车运行速度提高到140 km/h时，地铁列车气密性需达到6 s以上；而当地铁列车气密性小于2 s，地铁隧道净空面积则需要增大到35 m2以上；根据国内舒适性标准，若在现有地铁隧道断面情况下，将列车运行速度提高到140 km/h时，地铁列车气密性需达到10 s左右；而当地铁列车气密性小于3 s，地铁隧道净空面积则需要增大到35 m2以上。

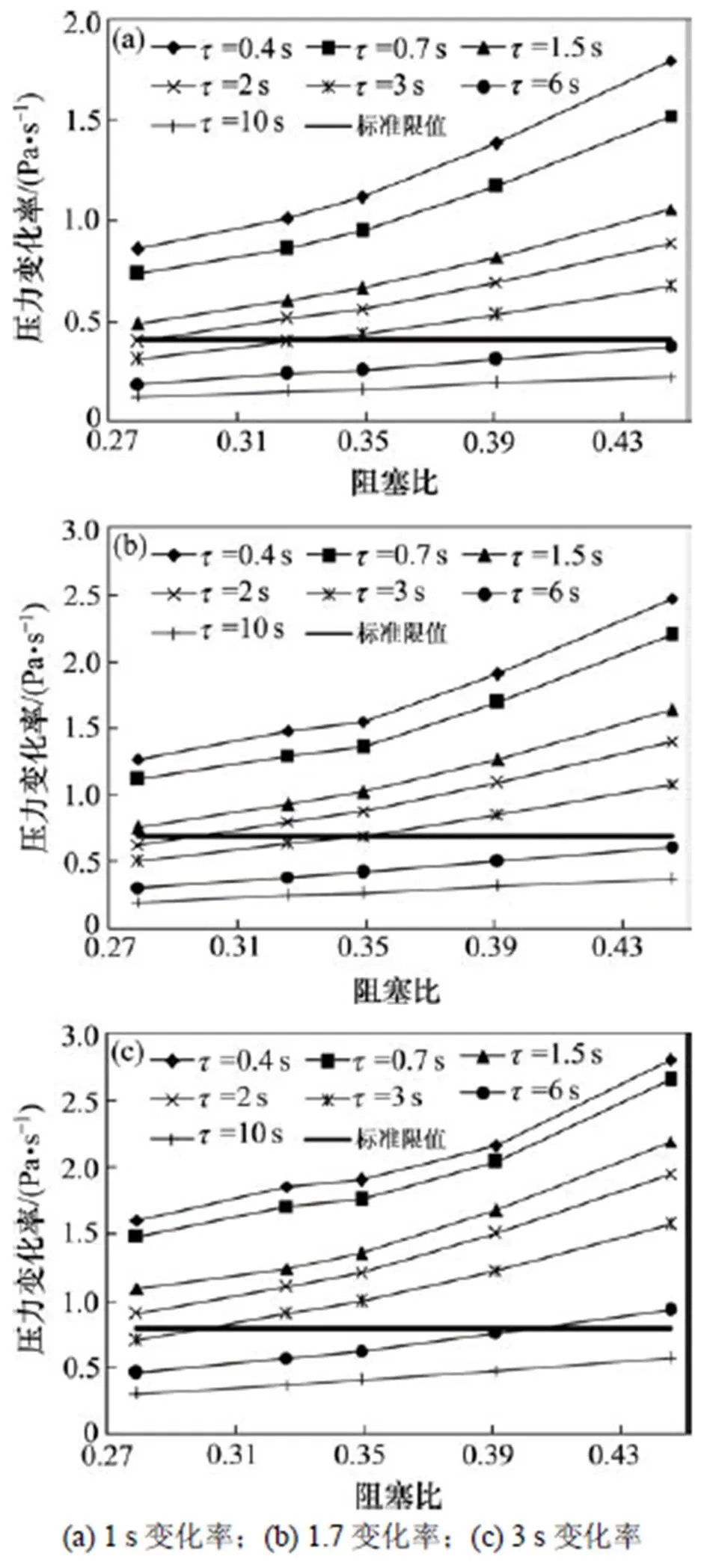
图11 列车匀速时最大车内压力变化率与阻塞比关系

列车以最高时速140 km/h进入隧道并在隧道内减速运行时，根据美国地铁标准在现有地铁隧道断面情况下，将列车运行最高时速提高到140 km/h时，地铁列车气密性需达到3 s以上；而当地铁列车气密性小于0.7 s，地铁隧道净空面积则需要增大到35 m2以上；根据国内舒适性标准，若在现有地铁隧道断面情况下，将列车运行速度提高到140 km/h时，地铁列车气密性需达到6 s以上；而当地铁列车气密性小于0.4 s，地铁隧道净空面积则需要增大到35 m2以上。

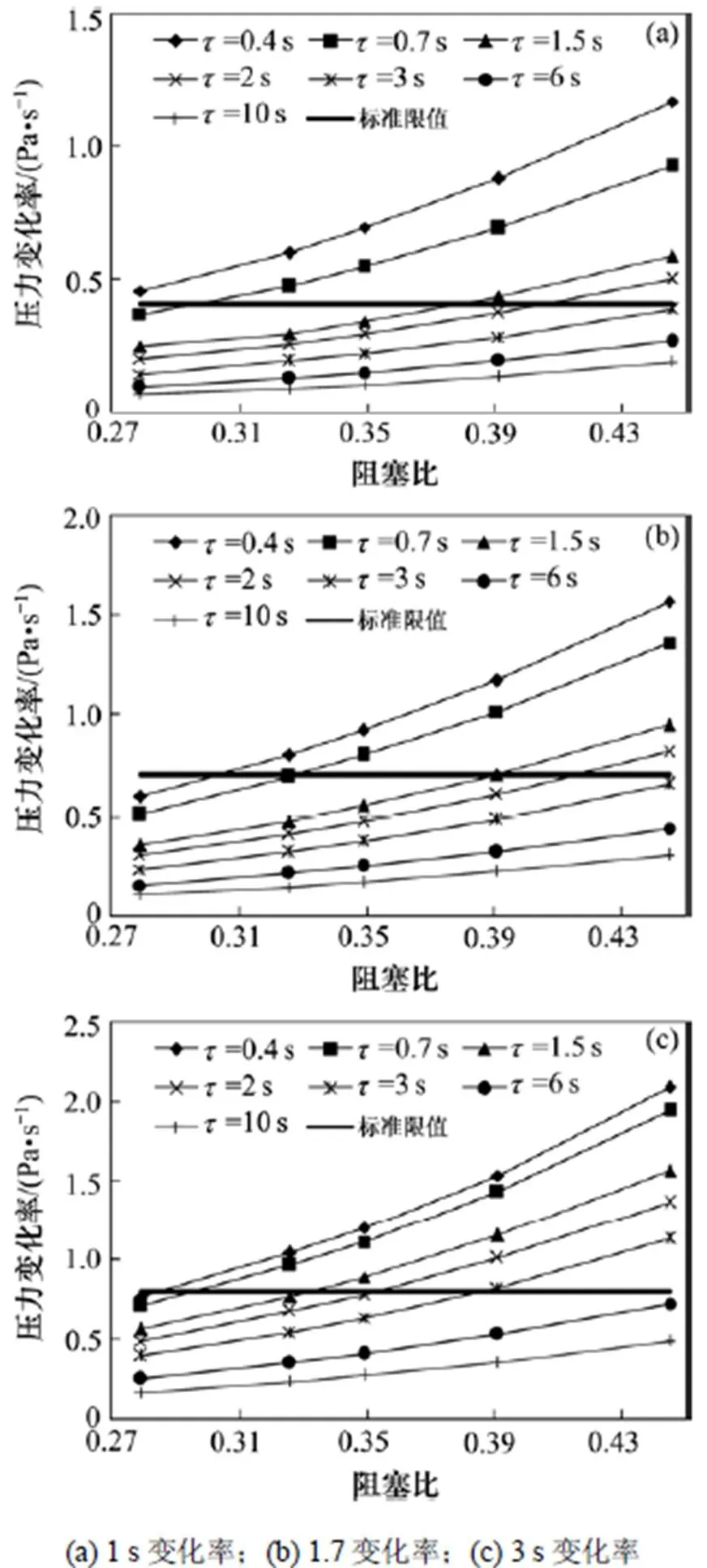
图12 列车减速时最大车内压力变化率与阻塞比关系

根据以上关系曲线分析得出，隧道净空面积A与密封指数的关系，如表2所示。

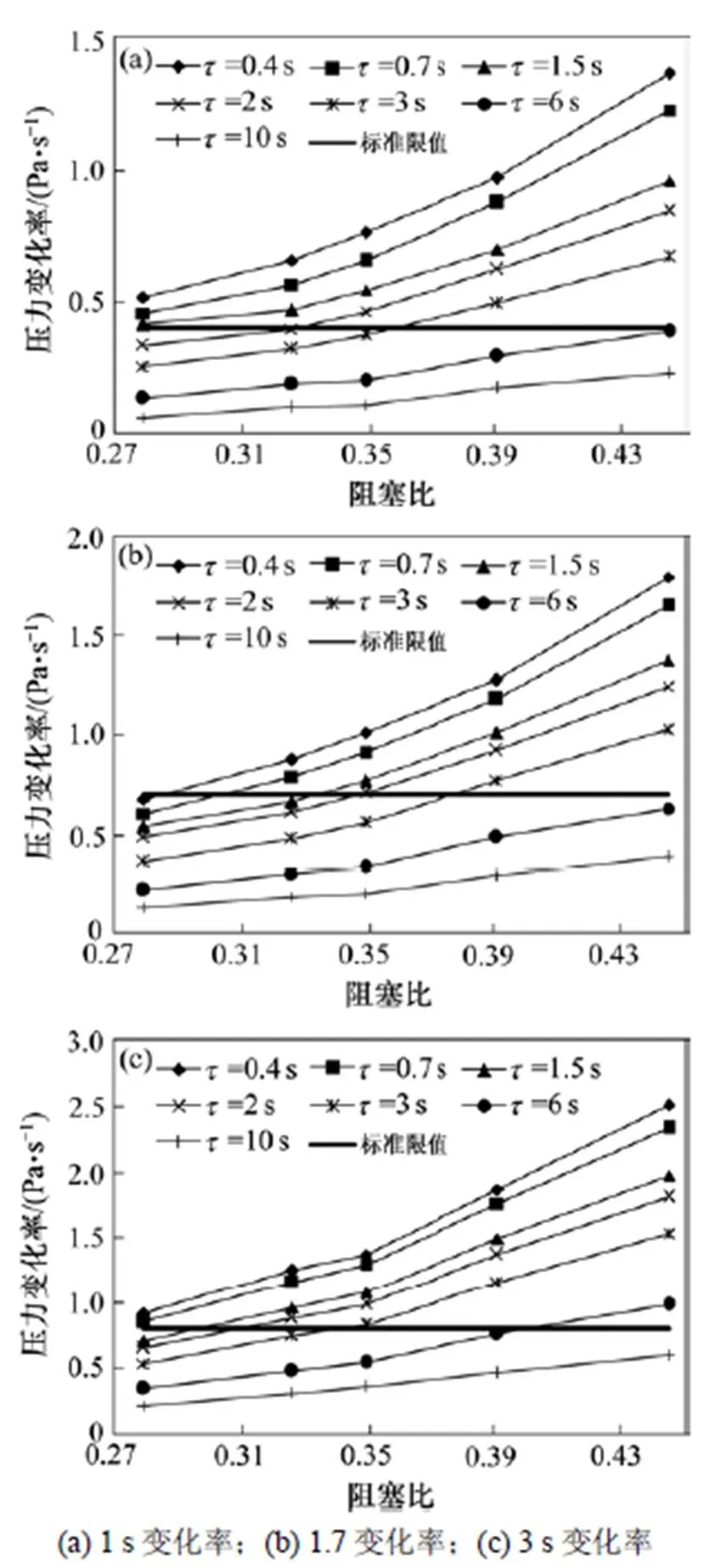
图13 列车加速时最大车内压力变化率与阻塞比关系

列车在车站启动并以最高时速140 km/h出隧道时，根据美国地铁标准，若在现有地铁隧道断面情况下，将列车运行最高时速提高到140 km/h时，地铁列车气密性需达到6 s及以上；而当地铁列车气密性小于1.5 s，地铁隧道净空面积则需要增大到35 m2以上；根据国内标准，在现有地铁隧道断面情况下，将列车运行最高时速度提高到140 km/h时，地铁列车气密性需达到10 s左右；而当地铁列车气密性小于1.5 s，地铁隧道净空面积则需要增大到35 m2以上。

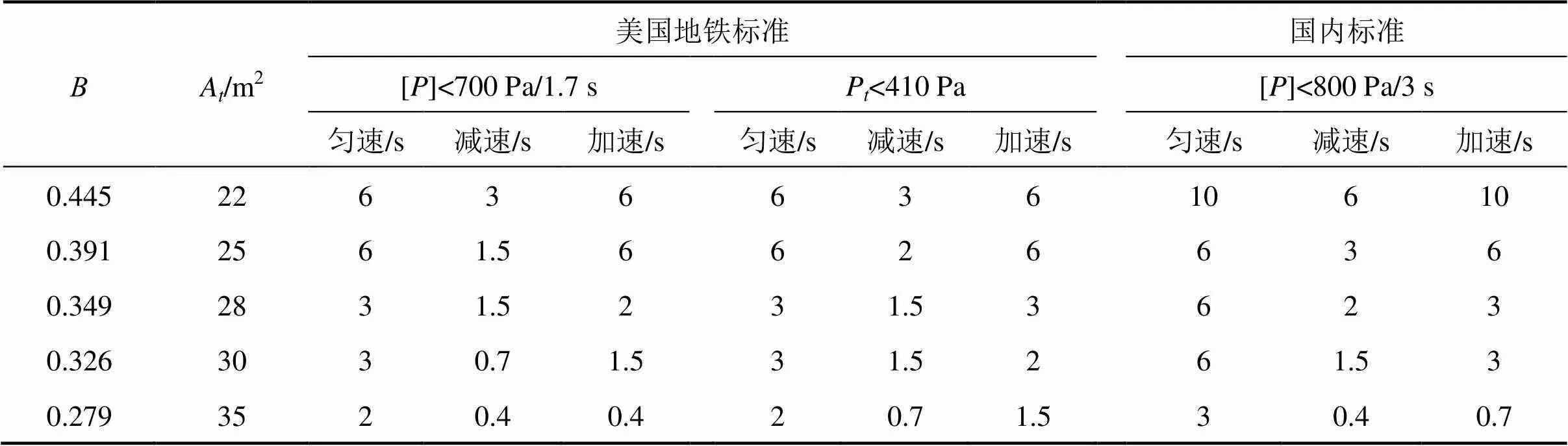
表2 隧道净空面积At与密封指数τ的关系

5 结论

1) 列车在隧道内运行时，阻塞比对测点压力幅值的影响主要源于对正峰值的影响。相同运行方式下，随着阻塞比的减小，测点压力(绝对值)和幅值随之减小，压力变化规律基本一致；阻塞比越小，列车表面测点压力幅值随列车长度方向的变化趋势越平缓。

2) 根据美国地铁标准，列车运行速度提高到140 km/h时，在现有地铁隧道断面情况下，列车以匀速、减速、加速不同方式运行时，列车气密性需分别达到6，3和6 s以上；隧道净空面积需小于35 m2时，列车气密性需分别大于2，0.7和1.5 s。

3) 根据国内舒适性标准，列车运行速度提高到140 km/h时，在现有地铁隧道断面情况下，列车以匀速、减速和加速不同方式运行时，气密性需分别达到10，6和10 s以上；隧道净空面积小于35 m2时，列车气密性需分别大于3，0.4和1.5 s。

[1] 祝岚, 张东, 孙振旭. 基于乘客舒适性的快速地铁隧道压力波分析[J]. 都市快轨交通, 2015, 28(1): 87−91. ZHU Lan , ZHANG Dong, SU Zhenxu, et al. Analysis of pressure waves of high-speed subway tunnel based on passenger comfort[J]. Urban Rapid Rail Transit, 2015, 28(1): 87−91.

[2] 李春超, 彭花, 左建勇. 地铁列车运行加减速度动态采集与特征分析[J]. 工业仪表与自动化装置, 2015(5): 25−27. LI Chunchao, PENG Hua, ZUO Jianyong. The collecting and character analysis of subway train running acceleration[J]. Industrial Instrumentation & Automation, 2015(5): 25−27

[3] MA Weibin, ZHANG Qiongli, CHENG Aijun, et al.Study on Influence factors and changing law of micro-pressure waves at tunnel portals of high-speed railways[J]. Journal of the China Railway Society, 2013, 35(5): 97−102.

[4] Rabani M, Faghih A K.Numerical analysis of airflow around a passenger train entering the tunnel[J]. Tunnelling and Underground Space Technology, 2015, 45(1): 203−213.

[5] Chu C R, Chien S Y, Wang C Y, et al. Numerical simulation of two trains intersecting in a tunnel[J]. Tunnelling and Underground Space Technology, 2014, 42(5):161−174.

[6] ZHAO Jing, LI Renxian, LIU Jie. Numerical simulation of aerodynamic forces of high-speed trains passing each other at the same speed through a tunnel[J]. Journal of the China Railway Society, 2010, 32(40): 27−32.

[7] Kim J Y, Kim K Y. Experimental and numerical analyses of train-induced unsteady tunnel flow in subway[J]. Tunnelling and Underground Space Technology, 2007, 37(22): 166−172.

[8] Marta López González. Numerical modeling of the piston effect in longitudinal ventilation systems for subway tunnel[J]. Tunnelling and Underground Space Technology, 2014, 40(2): 22−37.

[9] 梅元贵, 周朝晖, 耿烽, 等. 高速铁路隧道初始压缩波一维流动模型的数值分析方法[J]. 空气动力学学报, 2006, 24(4): 508−512. MEI Yuangui, ZHOU Chaohui, GENG Feng, et al. Numerical method of initial compression waves produced by a high-speed train entering a tunnel-hood based on one dimensional unsteady compressible flow model[J]. Acta Aerodynamic Sinica, 2006, 24(4): 508−512.

[10] 梅元贵. 高速铁路隧道压力波一维模型数值方法简介[J]. 隧道建设, 2007, 27(增2): 36−40. MEI Yuangui. One-dimensional numerical flow model of pressure waves induced by passage of high-speed trains in a tunnel[J]. Tunnel Construction, 2007, 27(Suppl 2): 36−40.

[11] 林世生. 关于广州地铁隧道空气动力学效应缓解措施的研究[J]. 隧道建设, 2013, 33(8): 38−46.LIN Shisheng. Study on aerodynamic effect mitigation measures for Guangzhou metro tunnels[J]. Tunnel Construction, 2013, 33(8): 38−46.

[12] 王秀珍. 地铁列车气动效应分析[J]. 中国科技信息, 2011(21): 91−92. WANG Xiuzhen. Analysis of aerodynamic effect of subway train[J]. China Aerodynamic Journal Electronic, 2011(21): 91−92.

[13] 李志伟, 梁习锋, 张健, 等. 竖井对隧道内瞬变压力的影响[J]. 中南大学学报(自然科学版), 2011, 42(8): 2514−2519. LI Zhiwei, LIANG Xifeng, ZHANG Jian, et al. Influence of shaft on alleviating transient pressure in tunnel[J]. Journal of Central South University (Science and Technology), 2011, 42(8): 2514−2519.

[14] LIU Tanghong, TIAN Hongqi, LIANG Xifeng, et al. Aerodynamic effects caused by trains entering tunnels[J]. Journal of Transportation Engineering, 2010, 136(9): 846−853.

[15] 张雷, 杨明智, 张辉, 等. 高速铁路隧道洞门对隧道空气动力效应的影响[J]. 铁道学报, 2013, 35(11): 92−96.ZHANG Lei, YANG Mingzhi, ZHANG Hui, et al. Influence of tunnel portals on tunnel aerodynamic effects in operation of high-speed railways[J]. Journal of the China Railway Society, 2013, 35(11): 92−96.

[16] 张雷, 田红旗, 杨明智, 等. 帽檐斜切式洞门斜率对隧道气动性能的影响[J]. 中南大学学报(自然科学版), 2013, 44(2): 817−822.ZHANG Lei, TIAN Hongqi, YANG Mingzhi, et al. Influence of tunnel aerodynamic effects by slope of hat oblique tunnel portal[J]. Journal of Central South University (Science and Technology), 2013, 44(2): 817−822.

[17] 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007.TIAN Hongqi. Aerodynamics of high speed train[M]. Beijing:China Railway Press, 2007.

Study on tunnel aerodynamic of subway train during acceleration

LIU Dongxue1, 2, JIANG Yanan3, YANG Mingzhi1, 2

(1. School of Transportation Engineering, Central South University, Changsha 410075, China; 2. Key Laboratory of Traffic Safety on Track of Ministry of Education, Changsha 410075, China; 3. China Railway Liuyuan Group Co., Ltd, Tianjin 300308, China)

Based on unsteady-equations of three-dimensional and compressible viscous fluid, the paper research the transient pressure variation on the car surface and the internal pressure on the condition that the A-type subway train accelerate in tunnel, analyzed the relationship between the tunnel clearance area and the seal index. The results show that when the train runs in tunnel, the pressure amplitude of the measuring point decreases with the decrease of the blocking ratio, which is mainly reflected in the influence of the positive peak value, and the pressure variation rule, is basically the same. Along the length of the train, the trend of the pressure amplitude variation is more gentle with the smaller the obstruction ratio. When the train runs in three modes, the air tightness of the train must reach 6 s, 3 s, 6 s according to the American standard, and 10 s, 6 s, 10 s according to national standard, in 22 m2subway tunnel. When the tunnel clearance area is less than 35 m2, the air tightness of the train should be greater than 2 s, 0.7 s, 1.5 s according to the American standard, and 3 s, 0.4 s, 1.5 s according to national standard.

subway train; numerical simulation; moving model experiment; acceleration; aerodynamic effect; blocking ratio

U270.11

A

1672 − 7029(2018)01 − 0178 − 10

2016−12−11

国家科技支撑计划资助项目(2015BAG12B01-24)

杨明智(1972−)，男，湖南望城人，副教授，博士，从事列车空气动力学研究；E−mail：yqyymz@126.com