球面近场天线测量系统校准中的一类不确定度分析*

周 峰， 孙景禄， 张碧慧， 吴 翔， 孙思扬， 袁修华， 张向阳

(1. 中国信息通信研究院 中国泰尔实验室， 北京 100191； 2. 中国人民解放军91668部队， 上海 200080)

随着4G/5G和NB-IOT等系统的发展， 无线通信系统中天线的部署数量日期增长， 同时天线向波束赋形和智能化发展， 天线在无线通信系统中的作用日益突出. 我国是移动通信天线生产大国， 出货量占据全球的70%以上. 这就给天线的测量工作提出了巨大挑战， 传统的远场测试系统速度较慢， 难以适应产业的发展. 近年来， 速度快、 可测量3D方向图的多探头球面近场测量系统得到了快速发展[1]， 我国深圳新益、 上海益麦、 法国Satimo等公司均研发销售该类测量系统， 中国信息通信研究院泰尔系统实验室就装备了这种系统， 我国的主要天线制造商华为、 京信、 盛路、 通宇、 捷士通等也都装备了多套该类系统.

众所周知， 准确的测试测量是质量的重要基础， 而测试系统的计量校准更是基础之基础. 本文重点讨论球面近场天线测量系统探头校准中的一类关键不确定度分量， 即校准用天线角度偏移引起的探头幅度相位一致性的不确定度.

1 空间角度误差引入的不确定度

以一个典型的球面近场测量系统为例： 系统安装在一个12 m×10 m×10 m的微波暗室内， 采用了127个正交双极化探头， 均匀地分布在一个内径为6.4 m的大圆环上， 能够在0.4～6.0 GHz频段范围内对圆环圆周上的电磁场进行实时采样测试， 系统的运动控制器通过步进电机， 驱动转轴， 从而带动天线转台旋转报杆及天线， 完成3维球面扫描测量过程.

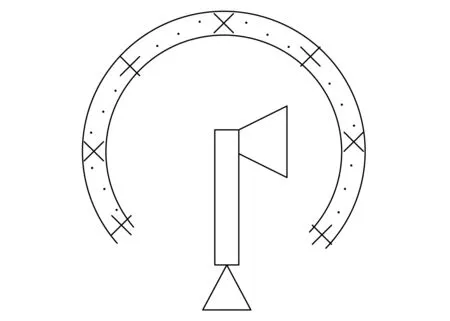
图 1 多探头球面近场探头一致性校准示意图Fig.1 Diagram of conformance calibration for multi probe spherical near field probe

显然， 在测量中， 探头一致性要求每个探头对相同输入的响应一致， 主要包含： 幅度均匀性、 相位均匀性. 场地鉴定时需要分别检测探头的上述性能.

多探头球面近场探头一致性检测示意图如图 1 所示[2].

在对球面多探头系统进行探头一致性测量和校准时， 为了得到准确的测量结果， 需要尽量保证标定天线与探头天线对准. 在实际操作中， 由于转台的步进精度、 对准误差等各项系统及操作误差的存在， 天线对准方向与理想情况之间总会存在一定的误差， 在校准用天线的坐标系上， 将水平角误差记为Δφ， 将垂直角误差记为Δθ， 则重点考虑：

对准角度误差导致标定天线最大增益方向偏离探头方向， 从而导致探头接收信号强度产生相对误差； 同时使得标定天线距探头的距离发生变化， 从而导致探头接收信号相位产生相对误差.

这种相对误差就是一个需要考虑的不确定度来源.

2 校准用天线建模和分析

为了分析上述不确定， 就需要分析典型的校准用喇叭天线的方向图特性， 为此， 我们根据典型的天线构造[3]， 建立了FDTD仿真模型， 如图 2 所示， 进而获取了包含幅度和相位信息的3D方向图数据， 如图 3 所示， 然后对幅度相位误差特性进行分析.

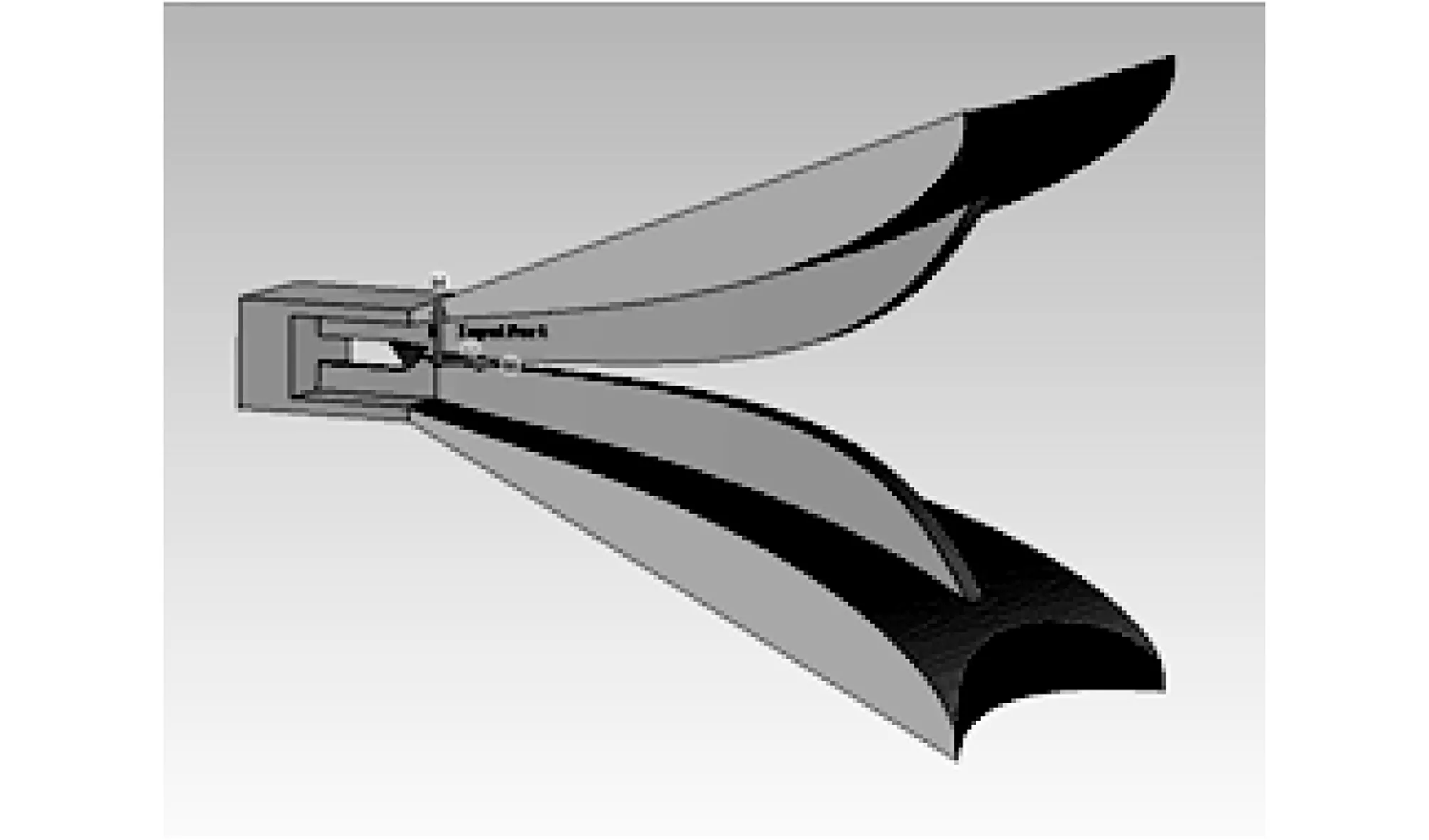
图 2 校准用喇叭天线建模Fig.2 Modeling of calibrated horn antenna

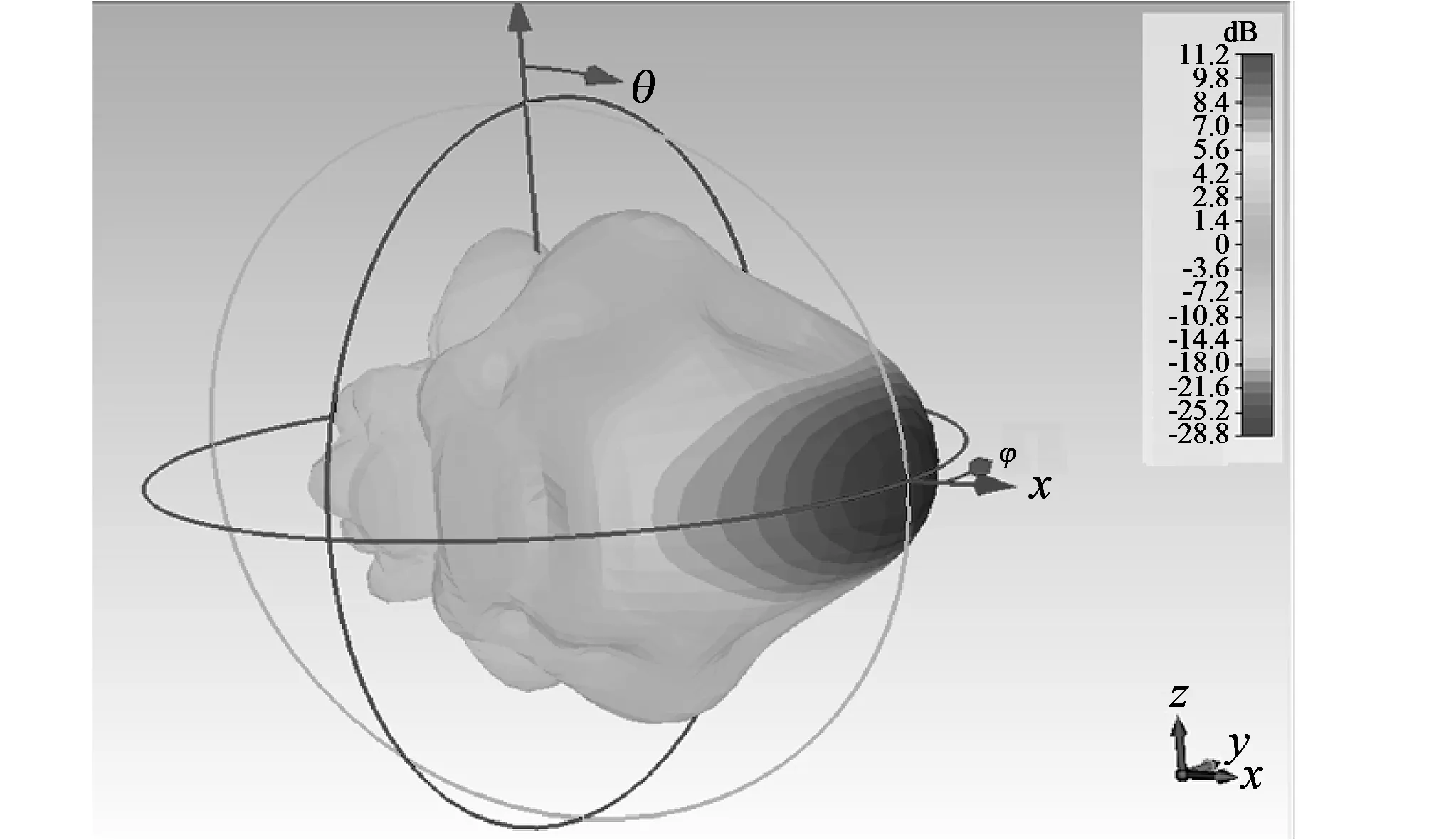
图 3 3D方向图(增益参数)Fig.3 3D antenna pattern(gain parameter)

需要指出的是， 在图 3 所示坐标系上， 在最大增益方向附近，θ是主要极化方向， 故而相位分析以电场Eθ为准. 进而分析其误差分布曲线. 由于分析图表较多， 摘其典型的如图 4～图 11 所示. 分析仿真结果， 有两个基本规律： 首先， 在角度误差较小时， 增益、 相位误差和角度误差呈线性关系， 这是因为在自变量变化较小时， 函数曲线趋近于直线段. 其次， 一般而言频率越高， 增益和相位误差越大. 考虑到水平角误差和垂直角误差呈平均分布， 取扩展因子, 则6 GHz以内标准不确定度分量概算表如表 1 所示.

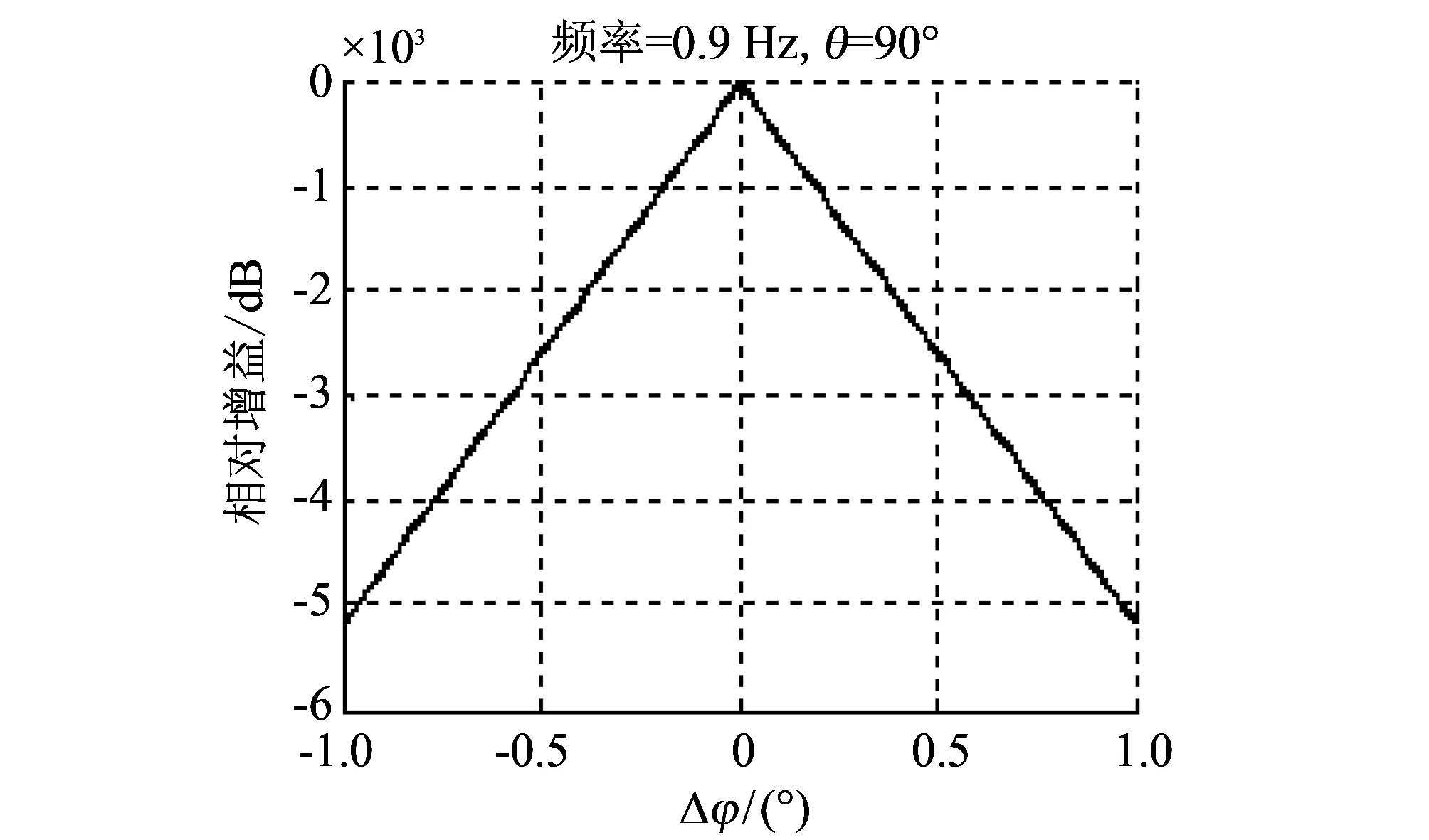
图 4 水平角误差Δφ引起的相对增益变化(0.9 GHz)Fig.4 The relative gain change caused by the horizontal angular error Δφ (0.9 GHz)

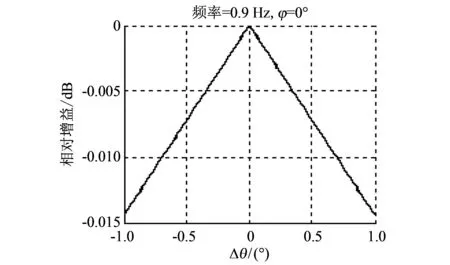
图 5 垂直角误差记为Δθ引起的相对增益变化(0.9 GHz)Fig.5 The relative gain change caused by the vertical angular error Δθ (0.9 GHz)

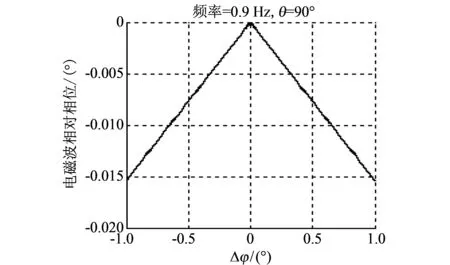
图 6 水平角误差Δφ引起的相对相位变化(0.9 GHz)Fig.6 Relative phase change caused by horizontal angular error Δφ (0.9 GHz)

图 7 垂直角误差记为Δθ引起的相对相位变化(0.9 GHz)Fig.7 Relative phase change caused by vertical angular error Δφ (0.9 GHz)

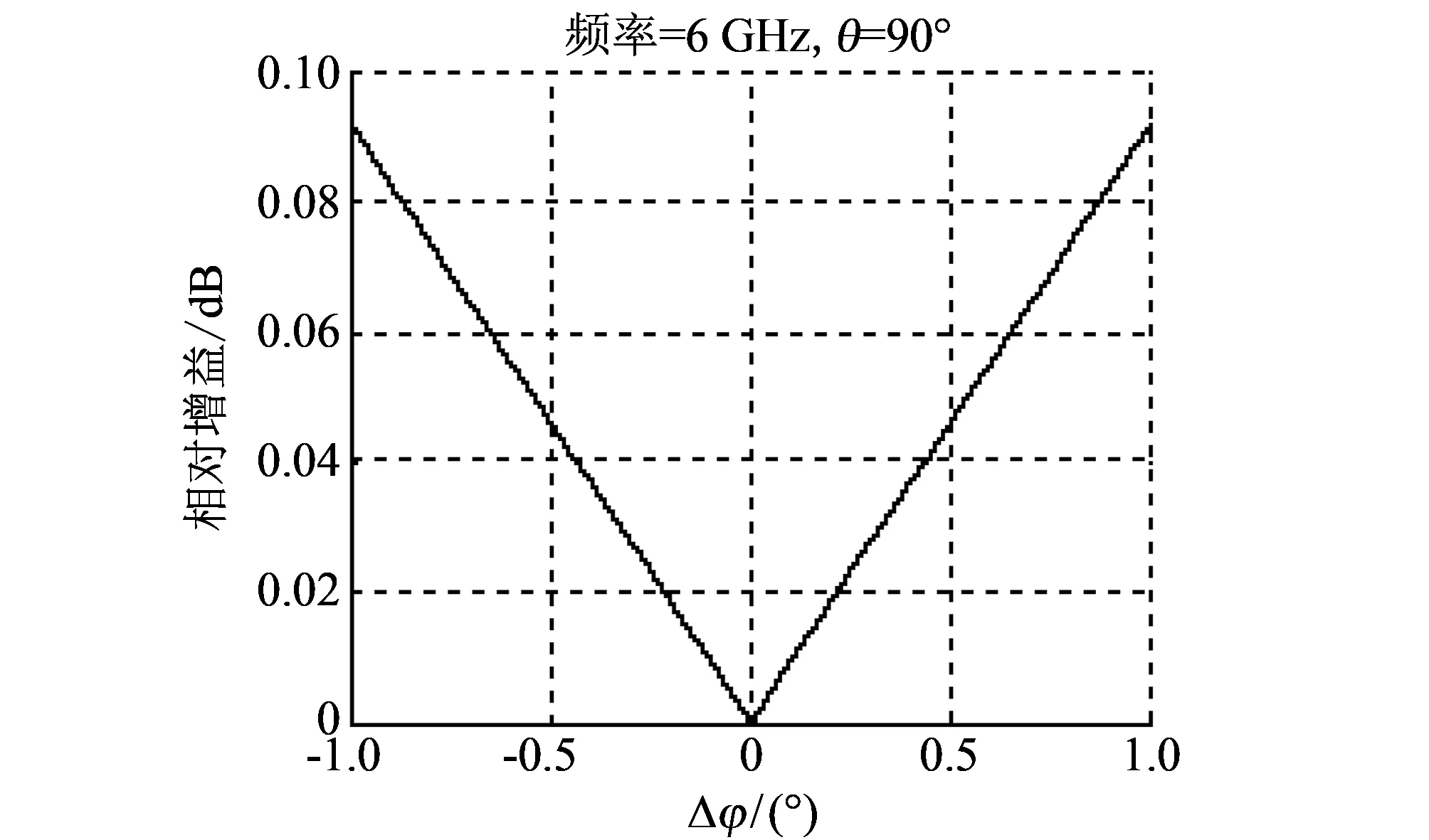
图 8 水平角误差Δφ引起的相对增益变化(6 GHz)Fig.8 Relative gain change caused by horizontal angular error Δφ(6 GHz)

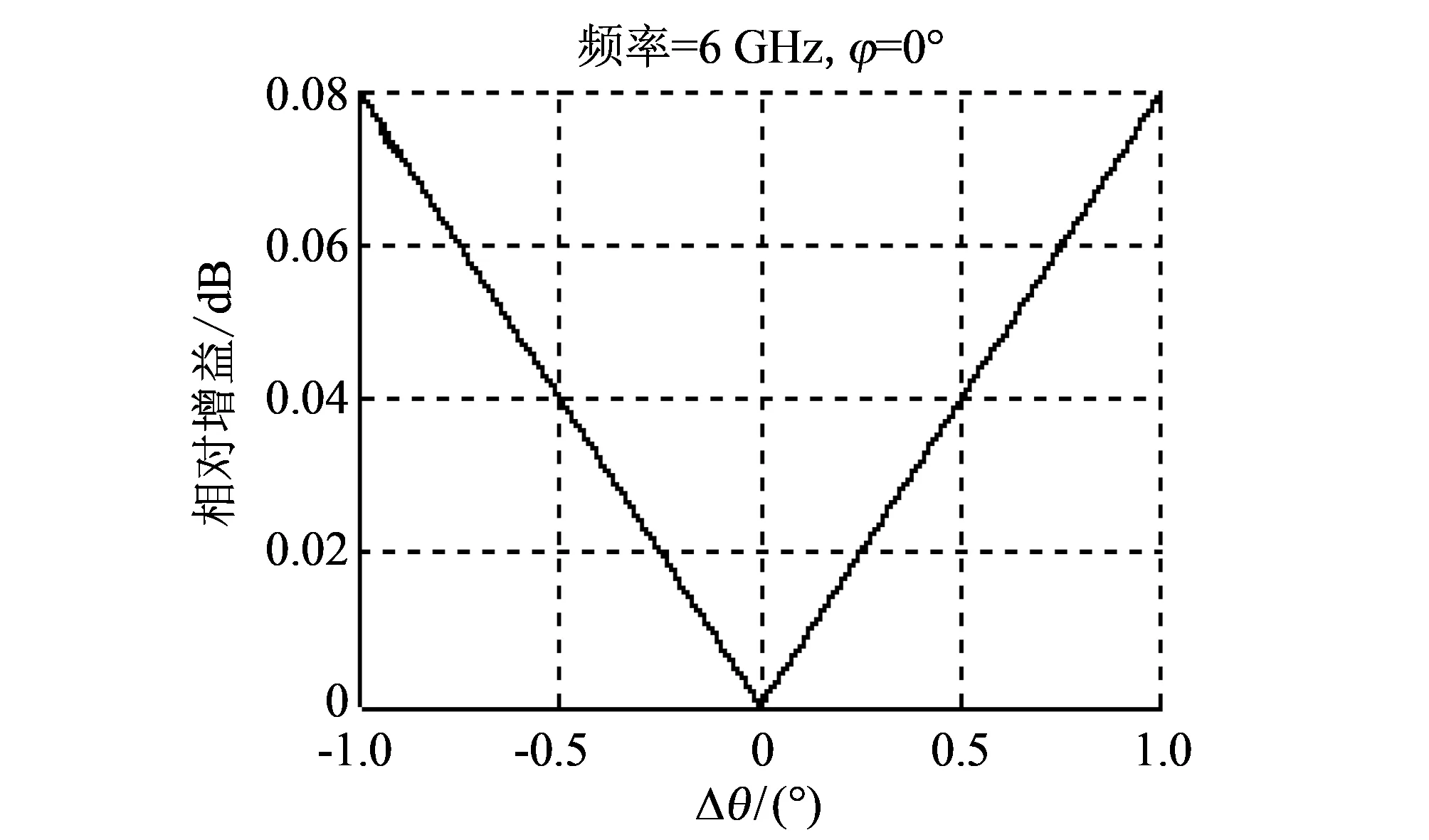
图 9 垂直角误差记为Δθ引起的相对增益变化(6 GHz)Fig.9 Relative gain change caused by vertical angular error Δφ(6 GHz)

在使用高精度机械臂的前提下， 水平角误差Δφ和垂直角误差Δθ控制在±0.5°以内是较容易的， 采用激光定位等手段， 可以控制在±0.1°以内， 结合表 1， 可以发现这类幅度不确定度在0.01 dB以内， 相位不确定度在0.03°以内， 是比较小的.

图 10 水平角误差Δφ引起的相对相位变化(6 GHz)Fig.10 Relative phase change caused by horizontal angular error Δφ(6 GHz)

标准不确定度分量来源表述ug-Δφ水平角误差Δφ引入的接收信号幅度不确定度0.09Δφ3,单位为dB,Δφ的单位为度ug-Δθ垂直角误差Δθ引入的接收信号幅度不确定度0.08Δθ3,单位为dB,Δθ的单位为度up-Δφ水平角误差Δφ引入的接收信号相位不确定度0.3Δφ3,单位为度,Δφ的单位为度up-Δθ垂直角误差Δθ引入的接收信号相位不确定度0.28Δθ3,单位为度,Δθ的单位为度

3 近场效应分析

如图 1 所示， 在典型的测量场景下， 校准天线到被校准探头的距离大约是6.4 m， 这个距离不能严格满足远场条件. 如笔者之前撰文分析[4]， 近场条件下天线的等效增益一般低于远场增益， 此外， 按照标准[5]所述使用菲涅尔积分的方法计算喇叭天线的近场等效增益可以发现： 距离越近， 增益越小. 一般而言， 增益越小则意味着在最大增益方向上增益随着空间角度变化的梯度较远场方向图对应的梯度小， 故而： 即使考虑近场效应， 真实的不确定度分量也要比表1所列的小， 所以使用表 1 所列典型值计算， 是稳妥的、 保守的.

4 结 论

球面近场天线测量系统多探头校准中存在一类不确定度分量， 即校准用天线角度偏差引起的探头幅度相位一致性的不确定度. 本文根据典型的天线构造， 建立了FDTD仿真模型， 获取了包含幅度和相位信息的3D方向图数据， 进而对幅度相位误差特性进行分析. 分析表明： 首先， 在角度误差较小时， 增益、 相位误差和角度误差呈近似线性关系； 其次， 频率越高， 增益和相位误差越大. 本文给出了6GHz以内标准不确定度分量概算公式， 同时分析指出： 即使考虑近场效应， 本文所列概算公式也是稳妥保守的. 计算表明： 如空间角度误差可以控制在±0.1°以内， 这类不确定度是较小的.

[1] 周峰， 高峰， 张武荣， 等. 移动通信天线技术与工程应用[M]. 北京： 人民邮电出版社， 2015.

[2] 吴翔. YD/T 3182-2016 天线测量场地检测方法(行业标准)[S]. 中华人民共和国工业和信息化部， 2016.

[3] 赵建北. 超宽带TEM加脊喇叭天线特性研究[D]. 哈尔滨： 哈尔滨工业大学， 2013.

[4] Zhou Feng， Gao Yougang， et al. Distance boundary in antenna isolation calculation[C]. XXXI URSI General Assembly and Scientific Symposium， 2014.

[5] STD 1309-2013： IEEE Standard for Calibration of Electromagnetic Field Sensors and Probes， Excluding Antennas， From 9 kHz to 40 GHz[S]. p48-50. IEEE， 2013.