基于ADIS16488 MEMS IMU标定测试方法研究*

段祥玉， 蒋 伟， 杨功流， 王岁儿， 孙艺丁

(1. 河南思维轨道交通技术研究院有限公司， 河南 郑州 450001； 2. 北京航空航天大学 仪器科学与光电工程学院， 北京 1001912)

0 引 言

MEMS加工工艺的不断发展成熟， 使得MEMS加速度计和MEMS陀螺不断向高精度、 低成本、 低功耗发展， 微惯性传感器(陀螺、 加速度计)经历了单轴到3轴、 从单一惯性传感器到MEMS IMU 6自由度集成、 从6自由度到更多自由度集成化发展. 以ADIS16488战术级10自由度惯性传感器为例， 其集成3轴陀螺、 3轴加速度计、 3轴地磁传感器、 气压计及温度传感器[1]. 惯性导航系统是未来的发展趋势， MEMS惯性导航系统与光纤陀螺惯导系统将占据中低精度的主要市场[2]. 惯性导航系统具有自主性、 导航信息全、 实时性强等优点， 同时存在系统误差随时间发散的缺点. 为了有效抑制惯性导航系统的误差， 需要分析惯性导航系统误差特性， 从而有效抑制惯性导航系统误差的发散. 惯性导航系统误差包括确定性误差、 随机误差、 计算误差等， 其中确定性误差可通过标定方法补偿. 因而研究MEMS IMU标定方法、 分析MEMS陀螺及加速度计组件标定误差模型、 建立MEMS IMU准确标定误差补偿模型是十分重要的[3-5].

MEMS IMU中加速度计组件通常采用分立式标定方法， 利用转台提供高精度空间角位置信息， 对于MEMS加速度计以当地重力加速度为激励， 采用24位置、 12位置、 8位置、 6位置等多位置法进行标定[6]； 而MEMS陀螺组件采用速率法标定， 转台以一给定的正反转角速率作为标定模型输入信号[12]. 由于MEMS IMU精度较差， 很难用于长时间导航功能， 但是MEMS 惯性导航系统短时间精度较高， 通常与GNSS构成组合导航系统. 对MEMS IMU标定误差模型的精确建模与标定补偿， 可以进一步发挥MEMS 惯性导航系统优势， 可以保持较长时间自主导航精度， 在一些短时间GNSS信号失所的区域， 仍可以提供较高的导航精度. 本文以ADIS16488 MEMS IMU作为为研究对象， 针对性地对其标定误差模型及精确建模展开研究. 基于高精度3轴位置、 速率转台， 设计了6位置、 正反转速率法对加速度计和陀螺进行标定试验， 并对MEMS 陀螺及加速度计组件标定方程进行详细推导， 推导了MEMS IMU标定最小二乘法矩阵方程， 最终利用最小二乘法对MEMS IMU最优标定系数进行求解. 将计算的标定参数带入试验数据， 通过标定误差补偿前后对比， 验证本文方法可以快速有效地标定MEMS IMU， 该标定方法及最小二乘标定参数辨识可以推广应用于MEMS IMU及多批量标定.

1 MEMS IMU标定技术研究

1.1 MEMS IMU标定误差模型

1.1.1 3轴MEMS陀螺组件标定误差模型

3轴MEMS陀螺组件数学模型表述为

(1)

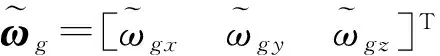
1.1.2 3轴MEMS加速度计组件模型

3轴MEMS加速度计组件数学模型表述为

(2)

1.2 标定方法

1.2.1 多位置MEMS加速度计组件标定

通常加速度计组件采用高精度位置转台多位置法来进行标定， 利用转台提供基准坐标系与当地重力加速度矢量gn， 通过已知转台位置信息和MEMS 加速度计组件量测信息， 可以计算加速度计组件标度因数、 安装误差、 偏置等标定系数. 常用惯导系统加速度计多位置标定方法有6位置、 8位置、 12位置、 24位置、 48位置等， 而24， 48等位置多应用于高精度惯导系统， 对于MEMS IMU标定通常采用6, 12, 24位置标定， 考虑到标定时间与标定补偿精度间的关系， 选择MEMS加速度计6位置快速标定方法. 标定过程中转台的位置编排如表 1 所示.

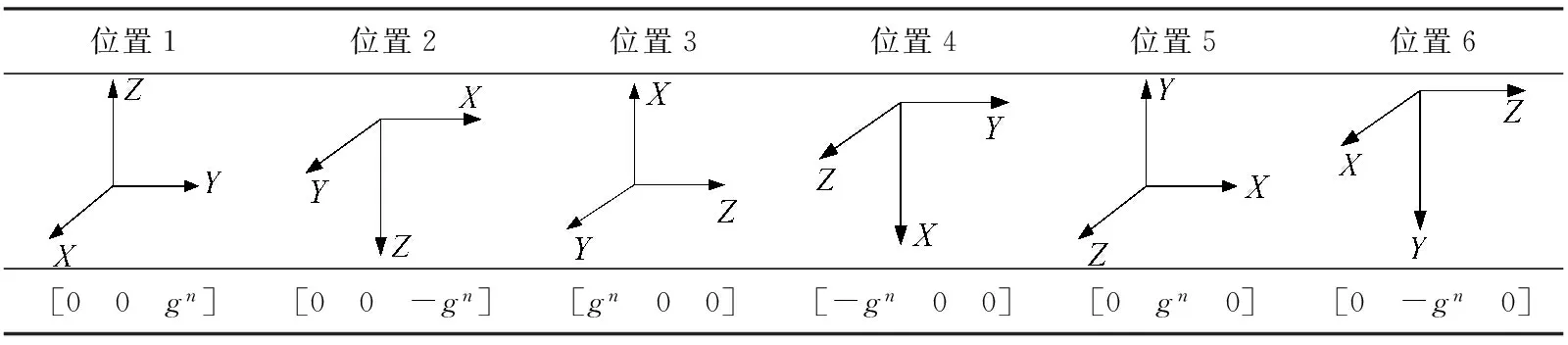
表 1 MEMS加速度计6位置标定编排

1.2.2 MEMS陀螺组件速率标定法

MEMS陀螺的标定通过速率转台精确的角速率作为基准角速率输入信息， 激励出MEMS陀螺标定误差， 从而获得MEMS陀螺的标度因数、 轴间安装误差以及陀螺零偏等标定系数. 对陀螺组件的标定通常需要根据载体的机动情况选择相应转台输入角速率. 由于陀螺仪技术相对于加速度计技术发展相对滞后， 但是陀螺仪在惯性系统中所占比重相比加速度计更高， 因此， MEMS陀螺标定选取不同组转台正反角速度对作为MEMS陀螺标定的输入信息， 本文MEMS惯性导航系统应用于车载导航定位系统， 因此选择如下的速率标定编排， 如表 2 所示.

表 2 MEMS陀螺速率法标定编排

通常选用一组正反转速率就可以实现陀螺仪参数的标定， 本文对陀螺的标定选取速率较多， 实际工程应用MEMS系统的标定根据器件精度和应用需求酌情考虑转台角速率输入组数.

1.3 数据处理

1.3.1 MEMS加速度计标定系数计算

MEMS加速度计的标定实质是当地重力场(1 g)内实现的标定， 虽然加速度计的标定系数包括标度因数、 零偏、 安装误差、 二次项误差(15个)， 但是高精度位置转台使得平行于垂向轴的MEMS加速度计敏感当地重力加速度， 而水平两个轴向的加速度计为0， 从而使得MEMS加速度计方程组解耦， 将每个位置的量测方程式(3)对X轴向加速度计列写方程式(4)， 根据方程组解的相关理论知识， 可知最少采用5位置就可以计算出MEMS加速度计的标定系数.

(3)

(4)

式中：i={1,2,3,4,5,6}， 表示x轴加速度计第i个位置的量测量， 将以上矩阵方程可以简写为

y=Ax,

(5)

式中：A为X轴向MEMS加速度计输入激励矩阵；x为X轴向MEMS加速度计待定标定系数；y为MEMS加速度计， 很明显rank(A)=5， 利用最小二乘法求解

x=(ATA)-1ATy.

(6)

同理， 可以写出y,z轴向的加速度计的方程， 利用最小二乘可以求解标定系数.

1.3.2 MEMS陀螺标定系数计算

同上，X轴向MEMS陀螺不同角速率输入方程为

(7)

同理， 可以列写出y,z轴向MEMS陀螺标定方程， 采用最小二乘法即可对MEMS陀螺的标定系数进行求解.

1.4 试验验证

采用高精度的3轴位置、 速率转台、 ADIS16488 MEMS惯性测量单元、 信号采集电路及数据采集标定软件， 对上述的标定方法进行试验验证. 图 1 所示为MEMS IMU安装与3轴转台图示， 右上角为MEMS IMU固定在电路板上， 电路板固定安装在机箱底板上， 标定过程中机箱底板固定于转台内框安装面上. 图 2 为MEMS IMU标定数据采集上位机界面.

图 1 三轴转台Fig.1 3-Axis turntable

图 2 MEMS IMU数据录取及标定上位机Fig.2 The data collection and calibration software of MEMS IMU

标定试验步骤如下：

1) 将MEMS IMU安装于转台安装面， 尽量将MEMS IMU安装在位于转台台面中心位置， MEMS IMU的z轴垂直转台台面， MEMS IMUx轴、y轴与转台的中框、 内框平行.

2) 系统上电后短暂预热2 min， 等MEMS IMU输出稳定后， 按表1的位置操作转台， 待转台到某一位置稳定后采集MEMS IMU信息， 采集时间为2 min.

3) 遍历MEMS 加速度计标定的所有6个位置后， 完成MEMS加速度计标定数据采集， 接下来进行速率法标定MEMS陀螺.

4) 固定转台其他两框， 操作转台以表 2 设定角速率转动转台， 待转台转动稳定后采集MEMS IMU数据.

5) 遍历表2中的不同框轴和转速， 完成MEMS陀螺标定数据采集， 至此MEMS IMU标定数据采集完成.

6) 对标定采集的数据进行处理和参数计算， 利用MEMS同步数据采集标定软件， 读取MEMS IMU标定采集数据， 计算每组数据的均值， 采用最小二乘法进行标定系数的计算.

标定后MEMS加速度计的模型为

(8)

标定后MEMS陀螺误差模型为

(9)

2 标定后验证

将标定实验获得的MEMS加速度计标定系数带入标定误差模型， 分别对MEMS 加速度计标定实验6位置实验数据离线标定误差补偿， 标定前后MEMS加速度计误差如图 3 所示， 图3(a)为未进行标定误差补偿的加速度计在转台6个位置的误差； 图3(b)为进行标定误差补偿后的MEMS加速度计在转台6个位置的误差， 通过两者的对比发现： 经过标定补偿后， MEMS加速度计误差得到了有效的抑制， 对标定前后的 6个位置的数据进行统计， 见表3， 很显然， 经过标定误差补偿后， MEMS加速度计器件的性能有了显著的提高.

图 3 加速度计标定前后误差对比图Fig.3 MEMS accelerometers error comparison before and after calibration compensation

轴系x轴y轴z轴均值/mg未标定-1.98-3.656.34标定后-6.16e-77.83e-71.86e-7方差/mg未标定0.853.233.28标定后0.160.130.017

同理， 也将MEMS陀螺标定辨识出的标定系数带入标定模型， MEMS 陀螺标定误差补偿前后的误差如图 4 所示, 图4(a)为未进行标定误差补偿的不同角速率输入误差值， 图4(b)为标定误差补偿后的MEMS陀螺误差， 对MEMS陀螺标定很大程度上补偿了陀螺的标度因数误差和零偏， 使得MEMS陀螺能很好地跟踪输入， 提高了MEMS陀螺精度. 表 4 给出了MEMS陀螺组件标定前后的器件精度对比表， 结合表3和表4可以看出， 标定补偿后， MEMS IMU的性能指标提高了至少一个数量级， 标定误差补偿有效地消除了惯性器件的确定性误差.

表 4 MEMS 陀螺标定前后精度比对表

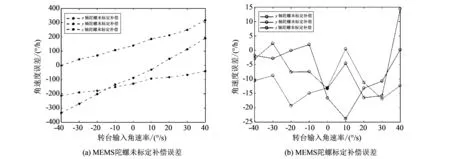
图 4 MEMS陀螺标定补偿前后误差对比图Fig.4 MEMS gyroscopes error comparison before and after calibration compensation

3 结 论

本文针对ADIS16488 MEMS IMU 标定方法展开研究， 通过建立MEMS IMU的标定误差模型， 设计了加速度计6位置法和速率法快速标定编排， 建立了基于加速度计及陀螺的标定误差模型， 推导了适用于最小二乘的标定参数辨识方程. 利用高精度3轴位置、 速率转台ADIS16488进行标定试验， 通过标定辨识参数对数据验证， 标定补偿后的输出值与理想输入值非常吻合， 验证了本文方法实用可行. 本方法还可以应用于由分立器件构成的MEMS IMU的标定中.

通过标定误差补偿， 有效地消除了惯性器件的确定性误差， 提高了MEMS惯性导航系统精度， 延长了MEMS自主导航精度保持时间， 在不改变硬件的条件下， 通过标定补偿使得MEMS惯性器件性能进一步提升.

[1] 魏爱娟. 一种提高MEMS微惯性航姿系统精度的方法设计与实现[J]. 舰船电子工程， 2017， 37(8)： 57-62.

Wei Aijuan. Design and implementatio to improve precision of MEMS micro inertial attitude system[J]. Ship Electronic Engineering, 2017, 37(8)： 57-62. (in Chinese)

[2] Perlmutter M, Robin L. High-performance, low cost inertial MEMS: A market in motion[C]. Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, 2012, 225-229.

[3] 向高林， 路永乐， 刘宇， 等. 基于改进六位置法的一种MEMS加速度计标定补偿方案[J]. 重庆邮电大学学报(自然科学版)， 2017， 29(1)： 62-67.

Xiang Gaolin， Lu Yongle， Liu Yu， et al. A calibration and compensation scheme of MEMS accelerometer based on the improved six position method[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition)， 2017， 29(1)： 62-67. (in Chinese)

[4] 于婷， 孙伟， 文剑. MEMS惯性组件的误差特性分析与标定[J]. 传感技术学报， 2016， 29(6)： 859-864.

Yu Ting， Sun Wei， Wen Jian. Error analysis and calibration of MEMS inertial components[J]. Chinese Journal of Sensors and Actuators， 2016， 29(6)： 859-864. (in Chinese)

[5] 石玺文， 李杰， 胡陈君， 等. MEMS三轴加速度计6位置标定方法的研究[J]. 电子器件， 2016， 39(2)： 403-406.

Shi Xiwen， Li Jie， Hu Chenjun ， et al. The research on six-position calibration of MEMS three axis accelerometer[J]. Chinese Journal of Electron Devices 2016， 39(2)： 403-406. (in Chinese)

[6] 黄苹. 捷联惯导系统标定技术研究[D]. 哈尔滨： 哈尔滨工程大学， 2005.

[7] 吴雪娟， 宋艳君， 黄树峰， 等. 一种MEMS陀螺仪的标定方法研究[J]. 传感器与微系统， 2015， 34(11)： 66-68.

Wu Xuejuan， Song Yanjun， Huang Shufeng， et al. Research of a calibration method for MEMS gyroscope[J]. Transducer and Microsystem Technologies， 2015， 34(11)： 66-68. (in Chinese)

[8] 任建新， 杜亚宁， 杨星辉， 等. 实用的MEMS惯性器件外场标定方法[J]. 传感器与微系统， 2014， 33(6)： 27-30.

Ren Jianxin， Du Yaning， Yang Xinghui， et al. Outfield calibration method for practical MEMS inertial device[J]. Transducer and Microsystem Technologies， 2014， 33(6)： 27-30. (in Chinese)

[9] 彭孝东， 张铁民， 李继宇， 等. 三轴数字MEMS加速度计现场标定方法[J]. 振动·测试与诊断， 2014， 34(3)： 544-548, 595.

Peng Xiaodong， Zhang Tiemin， Li Jiyu， et al. Field calibration of three-axis MEMS digital acceleration[J]. Journal of Vibration Measurement & Diagnosis， 2014， 34(3)： 544-548, 595. (in Chinese)

[10] 彭孝东， 陈瑜， 李继宇， 等. MEMS三轴数字陀螺仪标定方法研究[J]. 传感器与微系统， 2013， 32(6)： 63-65, 69.

Peng Xiaodong， Chen Yu， Li Jiyu， et al. Study on calibration method of MEMS 3-axis digital gyros cope[J]. Transducer and Microsystem Technologies， 2013， 32(6)： 63-65, 69. (in Chinese)

[11] 张红良. 陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究[D]. 长沙： 国防科学技术大学， 2010.

[12] 宋丽君， 秦永元. MEMS陀螺仪的一种实用标定法[J]. 压电与声光， 2010， 32(3)： 372-374， 378.

Song Lijun， Qin Yongyuan. A practical calibration method on MEMS gyroscope[J]. Piezoelectrics & Acoustooptics， 2010， 32(3)： 372-374， 378. (in Chinese)

[13] Song Lijun， Qin Yongyua. Six-position testing of MEMS accelerometer[J]. Chinese Journal of Sensors and Actuators， 2009， 22(11)： 1557-1561.