螺杆数学模型及数控加工铣刀廓形求解

王家祥，杨向红，孙建军

（天津工业大学机械工程学院，天津300387）

引言

梯形螺杆将旋转运动转换成直线运动、将扭矩转换成推力等优点而被大量使用在航空航天、海洋领域以及生产的各行各业。由于其截面型线的多样性和加工过程中空间啮合的复杂性，导致螺杆啮合间隙不均匀、运转振动大、齿间啮合出现局部干涉，使得梯形螺杆普遍存在啮合冲击大、寿命低等问题。贾寅等人基于螺杆真空泵针对单头梯形螺杆齿顶圆周螺旋升角小于齿根圆周螺旋升角,在两螺杆齿间啮合区，一螺杆的齿顶部分与另一螺杆的齿根部分上升速率不一，导致产生根切现象,即运动过程中出现二级转子齿间干涉[1]进行型线研究[2]。张世伟等针对单头等螺距梯形螺杆转子型线的干涉问题提出平移齿面法和内凹齿面法[3]，并未涉及各型线方程之间的一阶连续性问题。基于螺杆加工过程中的啮合情况，赵春秀等对成型铣刀加工螺杆过程的坐标计算进行了研究[4]，景宁等建立了圆柱立铣刀成型加工螺杆曲面模型[5]，Yang等使用逆包络法的思想建立了11∶6单螺杆压缩机的数字化模型并进行了加工刀具的设计[6]，王艳琴等建立并仿真了球头铣刀加工螺杆的过程[7]。刀具刃形的求解方法无法解决任意型线的情况，尤其展现于对螺杆齿形曲线的光滑连续性方面。本文采用内凹齿面法设计螺杆截面型线，解决了螺杆截面各型线之间的一阶连续问题，有效避免齿间干涉的出现，建立并解析出螺杆曲面模型。基于空间包络原理，对解析出的螺杆模型，将螺杆齿形离散成一系列离散点，研究螺杆于刀具加工过程中的空间啮合特性和几何特性，建立工件—刀具坐标转换方程，结合啮合原理解析出刀具接触迹方程、刀具轴向刃形。

1 螺杆三维建模

1.1 等螺距螺旋面方程

在图1中，该螺旋面是由曲线c沿着z轴方向作等速移动，同时沿着z轴作等速旋转形成，即由曲线c沿着轴向作螺旋运动形成。建立如图1所示的直角坐标系（x，y，z），三个坐标的矢量分别表示，引入端截面角度参数φ，可以得到已知的螺杆端截面曲线c的坐标方程为：

图1 螺旋曲面

若已知的螺杆端面廓形——曲线c绕着z轴转过一个角度θ，同时曲线c沿着z轴方向以导程pz上升一个距离时，引入螺旋参数p来表示，其中p=pzθ/（2π）[8-9]，则上式沿螺旋线形成的左螺旋面方程可以表达成：

右螺旋面方程则为：

式中：θ为角度参数，表示母线沿z轴转过的角度，沿着z轴看，以顺时针为正；p为螺旋参数，表示母线绕z轴转过单位角度，沿z轴方向移动的距离[10]。

由式（2）或式（3）可知，若以θ为常数，而只改变φ，可得到不同轴向位置处的端截面廓形曲线。反之，保持φ为常数，而改变θ，便可得到该螺旋面上的一系列螺旋线[11-12]。

1.2 单头等螺距内凹螺杆形线设计

螺杆的截面线型一般有对称圆弧型线、不对称圆弧型线以及新型不对称型线等，常用的是渐开线和摆线[13]。本文用渐开线、摆线和圆弧曲线作为所要设计的单头等距内凹螺杆的形线，如图2和图3所示。对于螺杆的左、右旋向而言，在实际制造过程中其线形设计基本参数一致，左右旋向不同，从而配对成一对螺杆转子。

图2 螺杆啮合半剖示意图

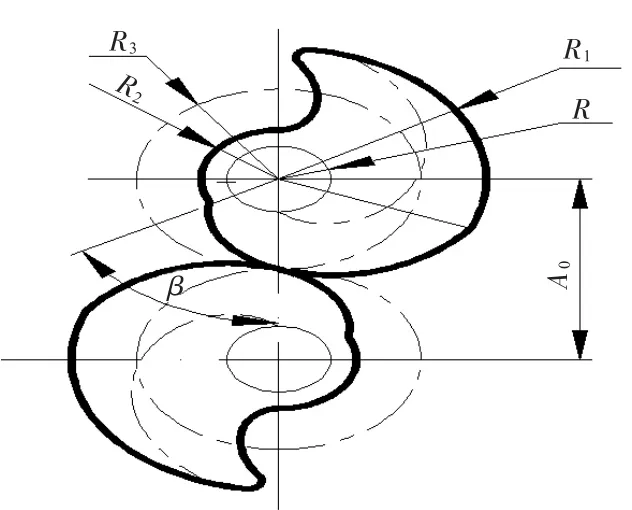
图3 螺杆截面啮合示意图

如图2所示，1为齿顶圆线形，2为渐开线线形，3为齿根圆线形，4为内凹摆线线形。螺杆啮合点处的端截面形线则如图3所示，主要参数包括：啮合中心距A0，齿顶圆半径R1，齿根圆半径R2，渐开线的生成圆半径R，理论啮合圆其半径R3，以及参数p（p=导程（/2π））。其中：

所设计的螺杆端截面各段截面形线方程分别为：

1）齿顶圆方程：

2）齿根圆方程：

3）渐开线部分是由标准渐开线方程先顺时针旋转π/2，同时为了使得啮合点位于两啮合圆心连线上，需再将渐开线方程顺时针旋转β角。本文中的渐开线方程是由标准渐开线方程经过这两步旋转变化所得，其方程的矩阵形式为：

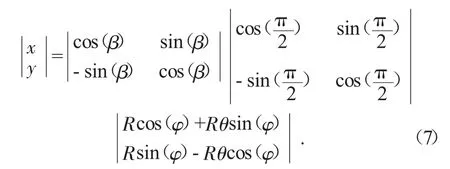
4）摆线部分亦是由摆线的标准方程逆时针旋转π/2所得，则其方程矩阵表达式为：

初步设计的截面形线中齿根圆与渐开线、渐开线与齿顶圆、齿顶圆与摆线相交点处一阶导数不存在，导致螺杆运动过程中产生较大的震动、两螺杆间啮合不顺畅，损耗螺杆的使用寿命，因而必须减少不可导点的出现。为了能够使得各段形线连接点处导数存在，本文采用圆弧过渡的方法：

齿根圆与渐开线部分采用外切圆弧过渡，设此圆弧方程为：

其中：（a，b）为过渡圆弧圆心点坐标，c为过渡圆弧半径。则联立公式（6）和（9）可得方程组（10），即可得到过渡圆弧与齿根圆的交点：

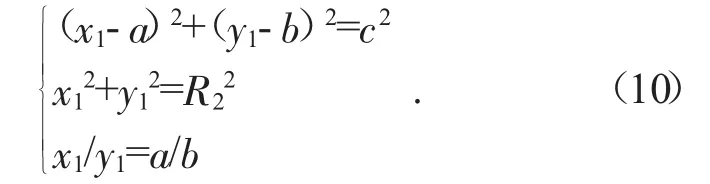
联立公式（7）和（9）可得方程组（11），即得到过渡圆弧与渐开线的交点：

通过给定过渡圆弧半径，求解方程组（10）（11），可得两个交点坐标（x1，y1），（x2，y2），由这两点坐标与过渡圆弧半径就可确定过渡圆弧圆心位置。此外把点（x1，y1）代入到公式（6），可求解出齿根圆终止角θ1；把（x2，y2）代入到公式（7），可求得渐开线部分的起始角θ2。

齿顶圆与渐开线采取内切圆弧过渡，同上可确定此时过渡圆弧圆心位置，并求解齿顶圆起始角与渐开线终止角。对于齿顶圆与内凹摆线处的过渡方式，可用内切圆弧过渡，求解出过渡圆弧圆心位置，并确定齿顶圆和内凹曲线的终止位置。

根据上文推导，代入各个参数的实际赋值（R=20，R1=80，R2=30，c=5），通过C语言编程计算，将求解出的数据用Grapher绘制，得到如图4所示含过渡曲线的螺杆数学模型图：

图4 螺杆数学模型图

2 刀具及工件坐标系的建立

考虑螺杆的实际加工过程，建立刀具模型，基于包络法加工螺杆[14]的过程确定工件和刀具坐标系的转换关系。由于铣刀在加工过程中一直处于旋转状态，所以可以将刀具模型简化为其旋转过程中形成的回转工作面，即将刀具的回转工作面作为所要建立的刀具模型。

如图5所示，使刀具沿着工件坐标轴x正方向由远及近进行运动，在工件和刀具达到接触时，接触点称为第一接触点即为刀具与工件接触的初始位置（初始切削点位置）。

2.1 铣刀方程的建立

成形铣刀工作的有效切削表面是其形成的回转面，其结构可以简化为如图6所示。

则刀具简化模型的轴向截形即刀具廓形方程可表示为：

其中：R表示刀具表面点刀刀具轴线的距离，zr表示刀具轴向坐标值，即刀具厚度。

2.2 刀具与工件坐标系的关系

图5 包络法加工示意图

图6 刀具简化模型示意图

3 刀触点轨迹的推导与验证

基于空间包络法，工件与刀具是点对点的接触切削，且工件表面曲线与刀具表面曲线是一对共轭曲线，则满足共轭曲线接触的三个基本条件[15]：

1）在接触点处位置重合；

2）在接触点处相切；

3）在共轭接触点处，该点处的瞬时运动速度方向必须垂直于该点处的公法面即垂直于两曲面内任意法线。

螺杆是由工件绕着C轴的旋转运动与刀具沿着螺杆z轴向的进给运动包络而成。若设取螺杆面上一点M（x，y，z），则该点相对于两个坐标系原点的径矢为：

设刀具回转角速度为ω2，工件螺旋面回转的角速度为ω1，并以pω1匀速沿螺杆z轴向平移以满足螺旋面自身的螺旋运动。

则M点处随螺旋面运动的线速度为：

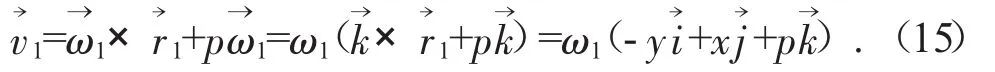
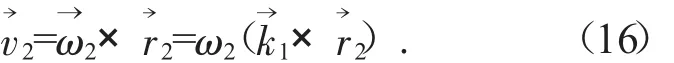
M点处随刀具运动的线速度为：将式（13）和式（14）代入式（16）整理得：由啮合原理可得：

根据右螺旋方程矢量表达式可以求解出右螺旋螺杆曲面上任意一点M（x，y，z）处的法矢量方程→n：

则由矢量运算法则得：整理式（20）、式（21）、式（22）可得：

称式（23）为右螺旋面特性方程。

同理可以得到左螺旋面特性方程：

将式（15）、式（16）、式（23）代入式（18），化简整理得：

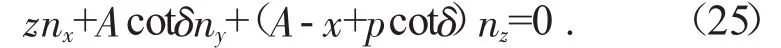
式（25）称为刀触点方程，在工件的端面截形上取一个定φ值，则可以通过式（25）可以求解出一个对应的θ值，表示工件截面上的一个坐标点按螺旋运动旋转过θ后成为接触点，将点（φ，θ）代入螺旋面方程就得到了一个接触点，一系列的接触点构成了空间的接触线（也称为接触迹）。将接触线绕着刀具回转轴线进行回转，可得到刀具的回转面。利用坐标变换式（13）将接触点转换到刀具坐标系O-XYZ中，得到坐标（x1，y1，z1），将一系列离散点通过转换方程求解出的坐标代入式（11）可得到铣刀轴向截形。

其中，取A0=140 mm，p=110.0/（2π），R=80.0 mm，δ=41.197352°，δ所取的值为被加工螺杆的螺旋升角，用C语言编程求解，可以求解出刀具廓形上的点，如图7所示。

图7 铣刀廓形截面点分布图

如图7所示，求解过程中存在导数无穷大点，所以求解处的廓形曲线上有突变点，对突变点处进行修整，整理数据可得到铣刀在廓形截面上的刀具厚度与半径之间的函数图像关系。对上图中的铣刀截形使其绕着刀具轴线R=0旋转一周即可得到完整的铣刀廓形。

4 结论

1）为避免齿间啮合干涉，针对单头等螺距梯形螺杆进行形线设计，解析各形线方程、起始点位置，求解出一系列的离散点坐标，并用Grapher进行坐标点图形绘制；

2）提出应用空间包络法加工螺杆，建立刀具与工件的坐标转换关系以及简化的刀具模型；

3）研究空间包络法加工工件的过程，并根据加工时刀具与工件所必须符合的啮合原理推导出刀触点方程，求解出刀位接触点轨迹的方程，通过C语言依据坐标转换关系编程解出工件上离散接触点对应的刀具接触点坐标，得出了刀具廓形。

[1]Stosic.N.On gearing of helical screw compress rotors[J].Proceedings of the Institution of Mechanical Engineers Part C:Journal ofMechanical EngineeringScience,1998,212(7):587-594.

[2]陈长琦，贾寅，郑定保，等.螺杆真空泵单头等螺距内凹转子型线研究[J].真空，2011（3）：8-11.

[3]张世伟，徐成海，祖文文，等.单头等螺距梯形齿螺杆转子型线的干涉问题研究[J].真空科学与技术学报，2007（1）：46-49.

[4]赵春秀，刘建宁.螺杆加工成型铣刀廓形坐标计算方法[J].机械设计，2008（6）：69-70.

[5]景宁，孙丽，王秀伦.用标准圆柱立铣刀加工成形圆柱螺旋曲面机理的研究[J].机床与液压，2001（4）：30-33.

[6]YANG，CHENGS.Modeling and manufacturing of pp-type single screw compressor[J].Transactions of the Canadian Society for Mechanical Engineering,2007,31(2):219-234.

[7]王艳琴.螺旋转子的几何建模与数控加工仿真[D].合肥：合肥工业大学，2006.

[8]张元勋，唐倩，江振伟，等.基于啮合间隙的螺杆齿形设计与成形加工方法[J].机械工程学报，2014（9）：48-57.

[9]姜淼.一种特殊螺旋曲面及其共轭曲面的研究[D].沈阳：沈阳工业大学，2009.

[10]万久远.特种供送螺杆关键技术研究[D].秦皇岛：燕山大学，2015.

[11]宋玉杰，王力，韩国有.基于UG的单螺杆泵参数化建模[J].油气田地面工程，2008（3）：23-24.

[12]STOSICN,SMITHIK,KOVACEVICA,et al.Geometry of screw compressor rotors and their tools[J].Journal of Zhejiang University，2011，12（4）：310-326.

[13]张世伟，徐成海，关奎之.螺杆真空泵单头变螺距螺杆转子型线的研究[J].真空，2002（4）：9-11.

[14]赵文珍，杨向红，孙新，等.包络法数控加工螺杆的刀具轨迹计算方法[J].组合机床与自动化加工技术，2000（5）：20-25.

[15]陈兵奎，梁栋，高艳娥.齿轮传动共轭曲线原理[J].机械工程学报，2014（1）：130-136.