涤纶织物热定型降耗优化算法
顾敏明, 戴文战
(1. 浙江理工大学 机械与自动控制学院, 浙江 杭州 310018; 2. 浙江工商大学 信息与电子工程学院, 浙江 杭州 310019)
织物在印染加工中,由于受到物理、化学的反复作用,容易造成褶皱、变形以及其他性能下降的问题。热定型可以使纤维结构进行重塑,织物的手感、滑移、颜色、幅宽、强力、外观等得到改善,进而达到织物所要求的服用性能[1]。它是印染行业后整理的一道重要工序,热定型工段的能耗占整个印染生产能耗的1/2左右[2]。对定型机热定型过程进行深入研究,优选工艺参数,有助于降低能耗,提升品质。
热定型过程复杂,工艺参数对织物定型品质影响较大,国内外专家开展了大量研究[3-4],主要集中在探讨各种热定型条件下不同织物的定型效果,研究揭示了热定型条件对织物结构和形态、纤维染色以及纤维强度等方面的影响,并且得到了定性或定量的结论,这些成果对定型机热定型工艺参数的设定具有指导作用。然而,这些研究大都是实验性研究,并没有建立数学模型。数学模型是进行参数优化的基础,对于织物干燥过程,不少学者建立了模型[5-7],而对定型机上连续热定型过程开展的分析与建模相对较少。文献[8]利用牛顿换热公式对热定型的过程进行了分析,建立了板式换热器的模型,文献[9]在上述基础上,利用多维度惯性权重衰减混沌化粒子群算法对生产过程进行优化,得到了相关的参数。由于所建立的过程模型复杂,因此涉及变量较多,不同织物的对象模型差异较大,生产新织物的热定型过程需要重新建模,优化策略复杂,该方法难以为实际工程人员所掌握,在一定程度上限制了其应用。此外,实际应用中,由于织物温度测量困难,工程上用烘房的温度来代替织物的温度,造成一定的差异[10]。目前对工艺参数的设定仍然主要依赖工程师经验,由于缺乏有效的数学模型,导致在热定型过程中,温度参数设置不合理,定型时间很难准确控制,能源浪费较多,亟待改进。
针对上述问题,本文从分析热定型生产过程出发,探讨各工艺参数对织物温度的影响,建立了织物温度估算模型,得到了织物的实时温度。在此基础上,提出能耗最小的优化目标,并利用PSO优化算法对各级烘房温度设定值进行优化,最终形成一种在保证产品质量的工艺参数约束的条件下,有效降低能耗的方法。
1 热定型过程分析与建模
1.1 热定型过程分析
热定型过程中待加工织物由进布架送入,经过平幅进布、红外对中、轧车、圆盘整纬、下超喂、机械整纬、螺纹扩幅、上超喂、剥边、探边、上针、浆边、拉幅热定形、冷风冷却、脱针、切吸边、冷水辊冷却、落布等工序,最终完成热定型。一般,定型机配置5~10节烘房,织物在热定型过程中,织物依次经过各节烘房,期间织物温度不断升高,直至达到热定型所需温度,即“热定型温度”,并保持稳定,直至离开烘房。对于干态织物热定型,该过程大致可用图1描述。

图1 织物热定型过程温度变化示意图Fig.1 Temperature variation of fabric during heat setting
定义织物从进入定型机加热直至达到热定型温度的这段时间为织物“加热时间”;定义织物达到热定型温度直至离开定型机的时间为织物“热定型时间”。织物在定型机烘房内的总时间是织物加热时间和热定型时间的加和。热定型对织物的要求是使织物在“热定型温度”持续“热定型时间”。
热定型过程中,烘房热量交换的过程如图2所示。首先,烘房内循环的空气和来自环境的冷空气经过换热器产生热空气,然后该热空气经由轴流风机引导至定型机的喷嘴,通过喷嘴产生热风冲击射流喷射到织物对其进行加热和热定型,在冲击射流作用下,织物温度按一定的规律发生变化。
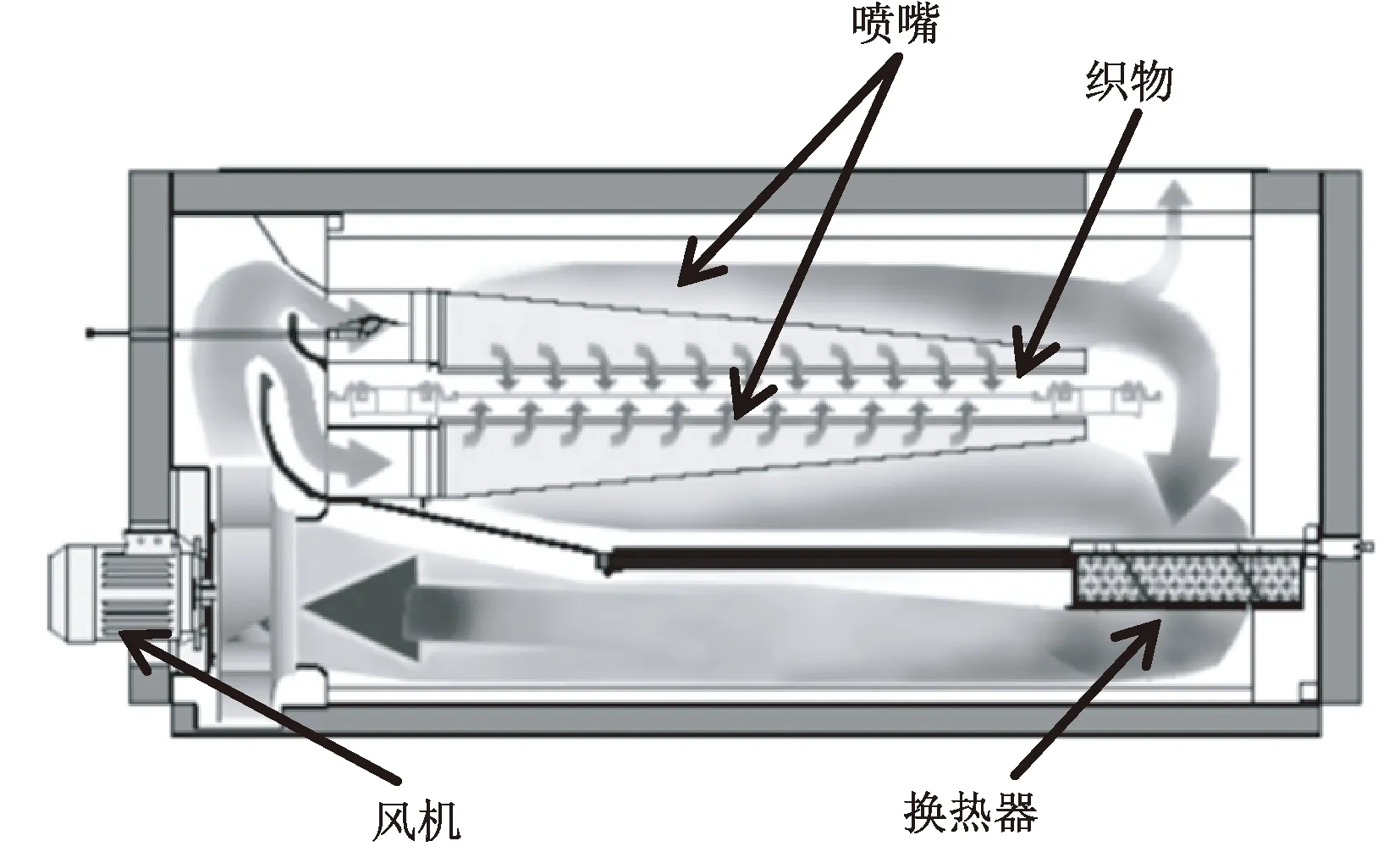
图2 定型机烘房热量交换过程示意图Fig.2 Schematic of heat exchanging in drying chamber
织物很薄,其在厚度方向上不存在断面温度差,即可认为织物内部和表面的温度场一致,在同一瞬间的温度都相等。为获取织物在运动方向上同一水平位置温度分布和风压分布情况,本文利用Fluent软件对烘房温度、压力进行数值模拟。为体现全面性,选取20余种不同烘房温度、风机转速条件进行仿真。限于篇幅,本文只取一种情况加以说明,定型机烘层的温度分布和风压分布如图3、4所示。
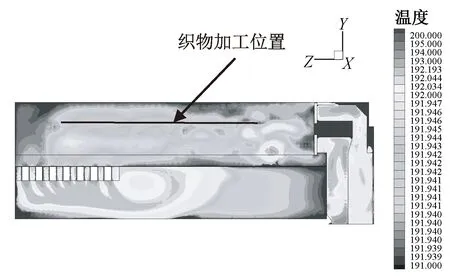
图3 定型机烘房温度分布图Fig.3 Temperature distributing of drying chamber

图4 定型机烘房压力分布图Fig.4 Pressure distributing of drying chamber
图3中烘房设定温度为190 ℃,电动机转速为1 200 rad/min。可看出,整个烘箱的温度相差不超过10 ℃,织物所处的位置温度分布相差不超过1 ℃,因此,沿运动方向上同一时刻织物各点温度能保证基本一致。由图4可看出,织物所处位置的压力基本均匀,相差不超过30 Pa,空气压力比较稳定。二者结果表明,待定型的织物在运动方向上同一水平位置各点的温度、压力稳定。
1.2 热定型过程建模
由仿真分析可知,在烘房喷嘴下方作业区域喷射的热空气温度、风压是均匀的。为建立干态织物热定型数学模型,本文进一步作了如下假设:1)假设喷嘴喷射的热空气是干燥的;2)假设待加工的织物基本干燥,在热定型过程中水分蒸发可以忽略不计;3)在一次定型过程中,热风速度一经设定,中途不再更改。
在加热和热定型过程中,取1个微元ΔS面积的织物,由于能量守恒,则单位时间内ΔS面积织物内部能量的增量等于热空气通过对流换热传递给织物的热量,对应关系为
(1)
式中:ΔS为选取织物的换热面积;Φ(t)为在热风射流单位时间内的换热量;h为对流换热系数;T(t)为单元织物t时刻后的温度;Tair(t)为t时刻热风射流的温度;ρp为织物的密度;cp为织物的定比压热容;t为织物加热过程时间;δ为织物厚度。
对式(1)进行变形,得到
(2)
令x=Tair(t)-T(t),则式(2)变为
(3)
式(3)是一阶齐次微分方程,其通解为
(4)
c为常数,设置初始条件,取t=0,T=T(0),T(0)等于环境温度,那么
x0=Tair(0)-T(0)
(5)
因此有
(6)
织物的温度可写为
(7)
在热定型过程中,烘房内的热空气温度在设定值不发生改变的情况下,温度变化比较小,因此,可认为烘房热空气的初始温度近似与t时刻温度相等,即Tair(t)=Tair(0),从而得到
(8)
定型过程中,织物本身的参数不变,即式(8)中ρp,cp,δ均是常数,因此,织物的实时温度主要跟换热系数h以及过程时间有关。考虑到影响换热系数h的因素众多,喷嘴的形状和排布、喷射距离、喷射速度以及织物特性等多个因素均对其有影响,很难用理论的方式求得准确的值。本文通过在不同条件下进行热定型实验,对实验数据利用MatLab的Curve Fitting Tool进行曲线拟合的方式来求取换热系数h。
1.3 模型的验证
选取涤纶织物进行实验,织物面密度为230 g/m2,幅宽为180 cm,定型机型号为韩国理和Glotech Platinum,10节烘房,烘房长度为3 m。本文选取了3组实验条件,对应结果如图5~7所示。图中,实线是模型输出,点是利用测量仪器进行测量的实际织物温度。图5、6中烘房温度设定值分别为180、190 ℃,图7中前5节烘房的设定值为180 ℃,后5节烘房的温度设定值为190 ℃。实验结果表明,本文模型可较好地匹配实际数据。

图5 180 ℃设定温度下织物实际温度和估算温度Fig.5 Estimated and actual fabric temperature when drying chamber temperature was set at 180 ℃

图6 190 ℃设定温度下织物实际温度和估算温度Fig.6 Estimated and actual fabric temperature when drying chambers temperature was set at 190 ℃

图7 变设定温度下织物实际温度和估算温度Fig.7 Estimated and actual fabric temperature under variable setting values of drying chamber
2 温度设定值优化
在热定型过程中,定型机中的热量损耗主要分为几部分[11],在不考虑蒸发的情况下,织物消耗的能量占7.1%,保温层热量损耗占6.5%,传动链条、布铗等机构占8.4%,空气加热占77.7%。显然,空气加热占用了最多的能量,这部分能量损耗可表示为
Qair=cairmair(ΔTair)=cairρairVair(ΔTair)
(9)
式中:Qair为加热空气所耗费的能量;cair为热空气的比热容;mair为热空气的质量;Vair为热空气的体积;ΔTair为空气经换热器加热后温度的增加值;ρair为热空气的密度。
在一次定型加工过程中,风机的转速保持恒定,所以空气的体积流量保持不变,因此,热定型过程的能量消耗值主要取决于空气温度增加值。由于环境温度不变,所以能耗大小实际取决于温度设定值。
为展开优化,本文采用1.3节的实验设备,涤纶织物的热定型温度为195 ℃,热定型时间为35 s,受限于其他织物特性,车速设定值不能大于25 m/min。经计算,为保证热定形时间,后5节烘房设定值设为195 ℃,因此,本文仅需对前5节烘房的设定值展开优化。
对式(8)通过实验数据拟合方式确定模型中各系数的值,得到经过各节烘房后织物温度的表达式:
yi=Xi-exp[-1.08×7.2](Xi-yi-1)
(10)
式中:Xi为各节烘房的设定温度;yi是在到达第i节烘房末尾时织物的温度;i=1,2,3,4,5。当i=1时,y0代表第0节烘房末尾的温度,即环境温度,取y0=30。数值7.2是在25 m/min的速度条件下,穿过1节烘房所用的时间。数值-1.08 =-h/ρpcpδ,它是换热系数和织物特性的一些系数的比值。
由分析可知,能耗大小取决于温度值设定值,为降低能耗,选取优化目标为各级烘箱温度设定值和最小,如式(11)所示:
(11)
按工艺条件,设定约束条件为
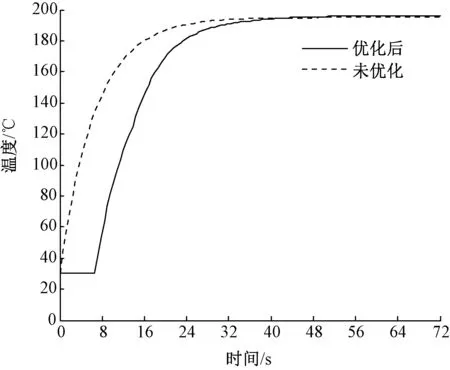
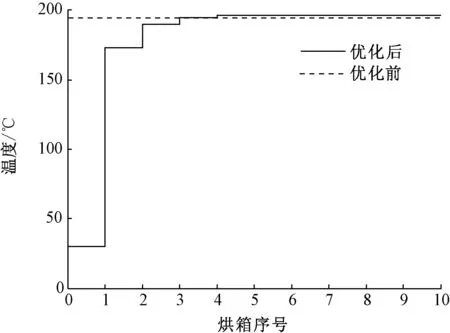
0 (12) |195-y5|<2.5 (13) 式(13)表示织物到达第5节烘房末尾时,温度要达到热定型温度要求。 针对上述优化目标,本文引入了粒子群算法,为防止陷入局部优化的陷阱,更快地得到优化值,本文根据已知对象模型和工艺特点,在约束条件式(12)的基础上对参数初始化的范围进行了调整,各级烘房温度设定值的初始化范围,优化结果和最终设定值如表1所示。 将烘房优化后的温度设定值与优化前进行对比,结果如图8、9所示。图8示出进入定型机烘房后不同时刻的织物实际温度的情况,其中实线是优化后的值,虚线为未优化的值。二者均能在经过5节烘房达到热定型温度,表明2种策略均能满足定型温度和定型时间的要求。图9示出织物在各节烘房热空气温度的设定值,显然,实线所代表的优化后的设定值加和要比优化前小,节能效果明显。 表1各级烘房设定温度值初始化范围及优化结果 烘房序号初始化范围优化结果设定值X130~20030.19930X2100~190173.061173X3150~200190.379190X4170~200195.014195X5180~200196.19196 图8 织物温度对比图Fig.8 Comparison of fabric temperature 图9 定型机温度设定值对比图Fig.9 Comparison of temperature set value 1)针对热定型工序的耗能问题,本文提出了一种涤纶织物热定型降耗的优化方法。以织物在定型机烘房加工过程的热力学特性为基础,建立了织物的实时温度估算模型,可较好地匹配织物的实时温度数据。 2)运用粒子群算法,以能量最小为优化目标,进行了烘房温度设定值的优化,在满足工艺约束的条件下,优化后的温度设定值可有效地降低能耗。 [1] ERTEKIN G, MARMARALI A. The effect of heat-setting conditions on the performance characteristics of warp knitted spacer fabrics[J]. Journal of Engineered Fibers & Fabrics, 2016, 11(3):64-71. [2] 任佳, 苏宏业. 印染热定型机煤、电能耗建模及优化求解研究[J]. 仪器仪表学报, 2013, 34(3):582-587. REN Jia, SU Hongye. Coal & electricity energy consumption modeling and optimal solution of fabric heat-setting machine[J]. Chinese Journal of Scientific Instrument, 2013, 34(3):582-587. [3] 尹丽敏,邓炳耀,刘庆生, 等. 热定型工艺对底网针刺造纸毛毯性能的影响[J].纺织学报, 2015, 36(3): 48-53. YIN Limin, DENG Bingyao, LIU Qingsheng, et al. Influence of heat-setting process on performance of batt-on-mesh papermaking felts[J]. Journal of Textile Research, 2015, 36(3): 48-53. [4] 孔清,崔宁,董知之, 等.拉伸热定型对PPS纤维结构与性能的影响[J].高分子材料科学与工程,2012,28(10): 85-89. KONG Qing,CUI Ning,DONG Zhizhi, et al. Effect of drawing and heat setting on structure and properties of poly(phenylene sulfide) fiber[J].Polymeric Materials Science and Engineering,2012,28(10):85-89. [5] AKYOL U, AKAN A E, DUARK A. Simulation and thermodynamic analysis of a hot-air textile drying process[J]. Journal of the Textile Institute, 2014, 106(3):260-274. [6] JOHANN G, SILVA E A, LIMA O C M, et al. Mathematical modeling of a convective textile drying process[J]. Brazilian Journal of Chemical Engineering, 2014, 31(4):959-965. [7] LEE H S, CARR W W, BECKHAM H W, et al. A model of through-air drying of tufted textile mater-ials[J]. International Journal of Heat & Mass Transfer, 2002, 45(2):357-366.. [8] 张益波, 任佳, 潘海鹏,等. 一类热定型机换热器的动态建模方法[J]. 化工学报, 2011, 62(8):2360-2366. ZHANG Yibo,REN Jia,PAN Haipeng, et al. A kind of dynamic modeling method for heat-exchangers of heat-setting machine[J]. CIESC Journal,2011, 62(8):2360-2366. [9] 蒋晓屾, 任佳, 顾敏明. 多维度惯性权重衰减混沌化粒子群算法及应用[J]. 仪器仪表学报, 2015, 36(6):1333-1341. JIANG Xiaoshan, REN Jia, GU Minming. Multi-dimensional descending chaotic inertia weight based PSO and its application[J].Chinese Journal of Scientific Instrument, 2015, 36(6):1333-1341. [10] 曾林泉. 纺织品热定型整理原理及实践[J]. 染整技术, 2012, 33(1):1-6. ZENG Linquan. Principle and practice of fabric heat-setting[J]. Textile Dyeing & Finishing Journal, 2012, 33(1):1-6. [11] HASANBEIGI A. Energy-efficiency improvement opportunities for the textile industry[EB/OL]. Lawrence Berkeley National Laboratory, Berkeley, CA.
Tab.1Initializationrangeandoptimizationresultsoftemperaturesetvalueofeachdryingchamber
3 结 论

