基于HALCON的机器人手眼标定精度分析与反演方法

杨厚易

(西南科技大学 信息工程学院，四川 绵阳 621010)

0 引言

视觉引导技术通过在机器人的控制环中加入视觉信息，使得机器人对环境有一定的感知能力，并通过视觉获取工作轨迹，引导机器人按照视觉给定的位姿工作。机器人视觉引导的优势主要体现在：(1)良好的适应性。对于同一生产线上不同拓扑结构的工件，可通过视觉获取不同工件的位姿信息，实现一机多工件操作。由于视觉信息的引入，也可较少地考虑工装过程中的工件误差，降低了系统加工成本。(2)非结构化环境的自动化。视觉引导通过引入视觉信息，使得机器人能够认知环境，收集环境信息并处理，达到工作环境的稳定和认知，使得机器人在未知环境中也能进行生产作业任务。

视觉引导技术可通过是否需要进行手眼标定来进行粗略的分类，对于需要进行手眼标定的视觉引导系统，其主要采用基于位置的视觉引导控制系统(PBVS)。PBVS系统中间变量传递的都是位姿信息，通过位姿信息在系统运动链中的传递与转换来控制机器人的运动轨迹。由于传递的是不同参考系下的位姿信息，坐标系之间位置关系的标定就显得尤为重要，这就要求高精度的机器人手眼标定。

无标定的视觉引导系统主要采用基于图像的视觉引导控制系统(IBVS)，IBVS系统通过建立图像空间与机器人空间之间的图像雅可比矩阵来控制机器人运动，其最大的优势在于只需要进行弱标定[1]甚至无标定[2]。而这种控制方法非常依赖对图像特征的提取，在工业应用中，大部分的工件并没有非常明显的特征，即使有明显的特征，视觉系统要对这些特征进行稳定的提取需要稳定的光源和高质量的相机。这种控制结构不依赖高精度的控制模型标定，但其控制过程中所面临的特征提取和稳定性等一系列关键问题使得无标定视觉控制系统在目前工业中很少得到应用，有学者针对无标定视觉引导技术的发展和前景进行了深入的分析和展望[3]。

本文针对工业应用较多的PBVS系统，在HALCON平台下使用线性标定法实现了固定相机结构下6DOF机器人手眼标定。通过对标定结果的反演，针对标定过程中图像数量和相机模型对手眼标定精度的影响进行了分析。

1 机器人的手眼标定

手眼标定是PBVS控制系统中极为关键的一环，对模型的标定精确度会直接影响机器人的作业准确度。PBVS系统中，根据视觉结构可分为移动相机结构(Moving Camera)和固定相机结构(Stationary Camera)。移动相机结构是将相机安装在机器人的本体上同机器人之间刚性连接，相机随着机器人手部的运动而运动。对于这种视觉结构，手眼标定的目的是计算机器人工具坐标系与相机坐标系之间的关系。对于固定相机的视觉结构，相机安装在环境中的某一个位置，相对于机器人的基坐标保持固定。在这种视觉结构下手眼标定的目的则是确定相机坐标系与机器人基坐标系之间的旋转位移关系。学者们对机器人的手眼标定方法进行了广泛而深入的研究，早在19世纪80年代，文献[4]就提出了称为Tasi两步法的经典手眼标定方法，通过将手眼位姿矩阵的旋转和平移两个部分进行分解，先求解转动部分，然后正交化旋转部分再求平移部分。在Tasi之后，Zhuang Hanqi[5]将机器人手眼转换部分与执行器进行整体建模，用于机器人运动学参数校准。文献[6]利用光流场的法向导数，采用两个微小平移来计算光轴方向，然后通过两个旋转计算平移部分。随着学者们的深入研究，各种高效的手眼标定方法也被相继提出[7-9],通过学者们对手眼标定的大量研究，PBVS控制系统在工业的各个领域得到了广泛的应用。

2 HALCON中的手眼标定

HALCON是由德国MVTec公司推出的一套标准的机器视觉库，集成了大量视觉算法，为手眼机器人的手眼标定提供了极大的便利。本文采用了线性手眼标定法，该方法默认相机是没有畸变的，即没有相机畸变的非线性影响。因此在进行手眼标定之前必须进行相机标定，获取相机内参数据，对图片进行畸变矫正。

2.1 线性标定原理

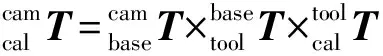
(1)

(2)

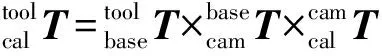
(3)

A=XB

(4)

(5)

该手眼标定方法就是线性标定法，也就是在默认相机没有畸变的情况下进行。为了取得较高的手眼标定精度，在使用HALCON进行手眼标定之前，必须进行相机标定。HALCON也为相机标定提供了快捷的方法，在HALCON的标定助手中，可以选择精度较低的线性相机模型(Division)，该种方法只能处理径向畸变；也可以使用精度较高的多项式模型，多项式模型下的标定精度更高，且能够对切向畸变有一定的补偿作用。对于手眼标定来说，可以采用更高精度的多项式模型来进行相机标定，提高手眼标定的精度。

2.2 机器人姿态信息的处理

对于不同的机器人，其采用的位姿表示法略有不同。绝大部分机器人的位姿表示法都以基坐标作为参考坐标系，位姿表示中的位置量没有什么区别，但姿态量的表示却略有不同。主要分为XYZ欧拉角、ZYX欧拉角和ZYZ欧拉角。以ZYX欧拉角为例，ZYX欧拉角姿态表示法首先将坐标系B与一个已知的参考坐标系A重合，将B坐标系绕着B坐标系的Z轴旋转α角，然后再绕变化后的坐标系B的Y轴旋转β角，最后绕又一次变化后的坐标系B的X轴旋转γ角。这种表示法中，每次都是绕运动坐标系B的各轴旋转，每次旋转所绕的轴的方位取决于上次的旋转。B相对于A的最终姿态可表示为(下标有撇号表示使用了欧拉角描述旋转)：

(6)

(7)

(8)

(9)

HALCON中的算子只支持RPY(固定轴)位姿表示法，RPY位姿表示法与欧拉角表示法的不同在于，RPY表示法中每次的旋转运动都是在固定(不运动)参考坐标系中确定的。在这种姿态表示法下，让B坐标系绕着固定参考坐标系A的X轴旋转γ角，再绕着固定坐标系A的Y轴旋转β角，最后绕固定坐标系A的Z轴旋转α角。B相对于A的最终位姿可表示为：

(10)

其中的旋转矩阵和欧拉表示法中的旋转矩阵相同，通过旋转矩阵的乘积结果来看，式(6)和式(10)的结果是等价的。可见三次绕固定轴旋转的最终位姿与以相反顺序三次绕运动坐标轴旋转的最终位姿相同，即ZYX欧拉角表示法等价于XYZ RPY角表示法。

在HALCON为每张图片匹配相应的机器人位姿数据时，首先要确认机器人所使用的参考坐标系和姿态表示法。如果机器人使用的是欧拉姿态表示法，在进行手眼标定时需要将姿态数据处理为RPY角的形式。

2.3 标定结果的反演

(11)

通过对标定结果的反演，可以直观地观察到手眼标定的精确度。

3 实验验证

实验使用了六自由度Kinova轻量型仿生机械臂和XB3相机，软件平台使用了HALCON13。标定板采用HALCON推荐使用的49圆标定板，尺寸为200 mm×200 mm。XB3相机的分辨率为1 280×960，焦距为3.8 mm，相机放置在机械臂的正前方约1 m的位置。标定板被粘贴到了一块亚力克板之上，亚力克板坚硬且轻盈，Kinova机械臂末端抓手可将其牢牢地抓稳，保证标定板不会在移动的过程中和工具坐标系发生相对位移。在进行手眼标定之前，XB3相机已经通过多项式相机模型进行了畸变校正。Kinova机械臂的工具坐标系位姿信息可以通过官方配套的DevelopmentCenter软件进行实时查看，需要特别注意的是，Kinova机械臂的姿态表示法为ZYX RPY角表示法，在调用HALCON算子制作机械臂姿态文件时要进行标识，告知HALCON关于机械臂的姿态表示方法。

通过使用HALCON进行手眼标定后对标定结果进行反演，在15张图片的情况下，结果如图1所示。从图1可以直观地看到，通过多项式相机模型进行镜头畸变矫正以后，标定的误差极小，通过对变量窗口中的数据进行对比，在图像坐标系中的位置最大误差为3.923 mm，均方误差为3.143 mm，角度最大误差为1.889°，均方误差为1.356°。

图1 反演后的结果(左:标定时提取的坐标信息；右:反演计算的坐标信息)

通过采集多组包含不同数量的带有标定板的图片集(不同图片集中图像不重复)，对反演计算出的图像坐标中的位置量和姿态量进行统计处理，绘制出了图2和图3的误差曲线图。从图2和图3中可以看到，使用更为精确的多项式摄像机模型能够提高手眼标定的准确度，在图片数量较少时，使用精确的摄像机模型可以降低位置误差和角度误差。当图片数量较多时，两种摄像机模型下的位置误差和角度误差都呈上升趋势。多项式模型误差曲线上升得较为缓慢，但使用线性模型的情况下，误差上升的趋势明显，这是由于线性模型对镜头畸变的修复能力有限，当图片数量增多时，会有更多的高维空间的数据点参与线性拟合过程。随着图片的增多，镜头畸变的影响越发明显。

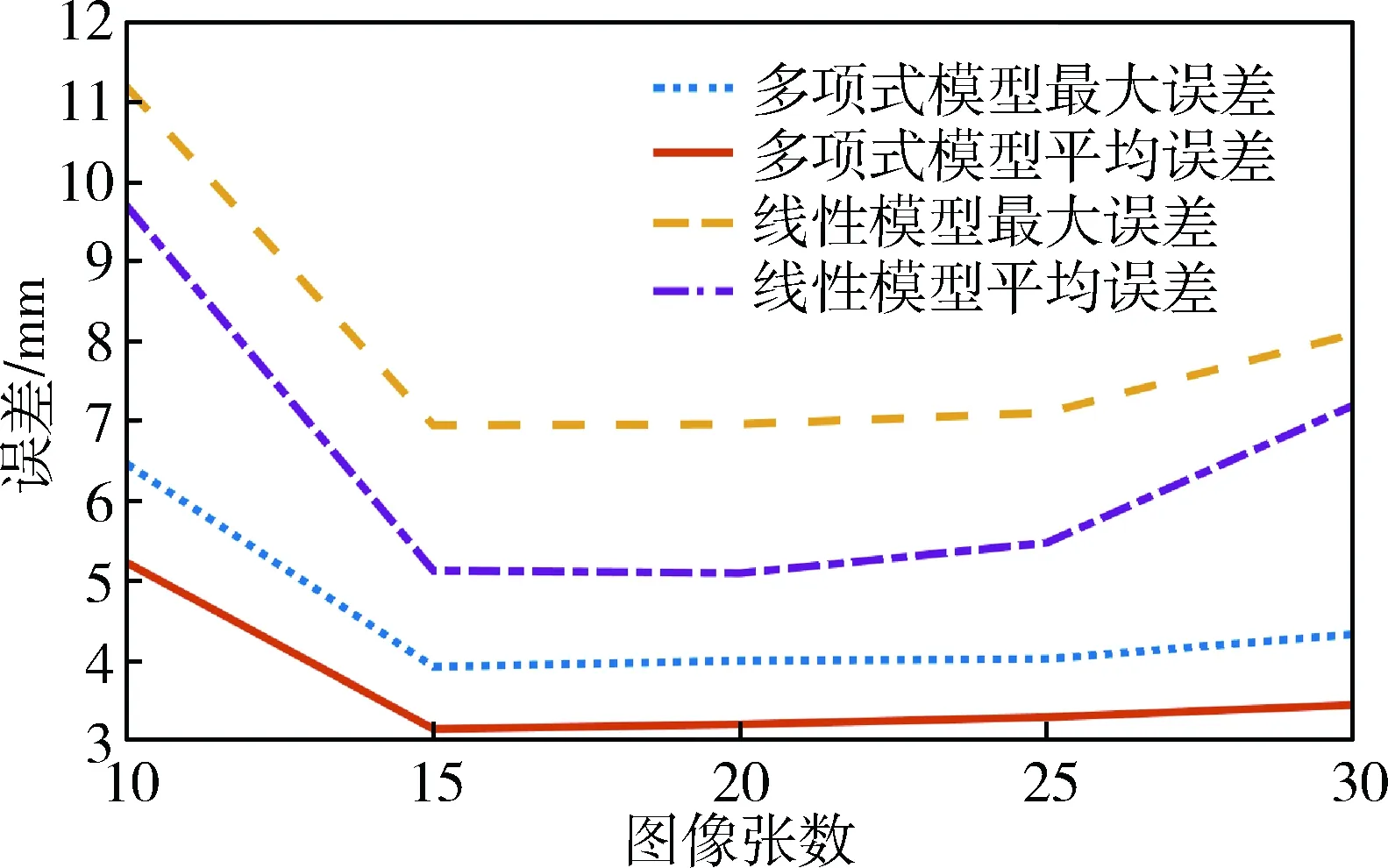
图2 位置误差曲线

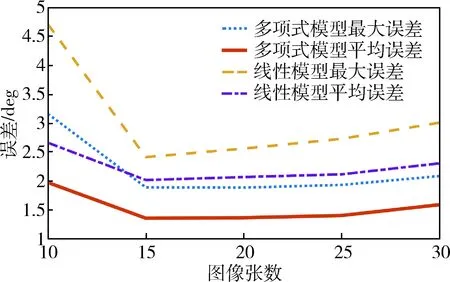
图3 角度误差曲线

当使用同样的摄像机模型时，在拍摄图片数量不足时误差较大。随着图片数量的增多，误差会达到最低，而当图片数量过多时，误差又开始增加，这也是由相机的畸变造成的。可得出结论，对于6DOF的Kinova机械臂，手眼标定采集的图像数在15～20张为宜。

4 结束语

本文通过HALCON平台提供的丰富的机器视觉算子实现了6DOF机械臂的手眼标定，阐述了线性标定的原理。实验标定精度达到了毫米级，可以满足生产线上一般工件的抓取任务进度要求。研究了不同图像数量和不同相机模型对手眼标定的精度影响。实验证明对于6DOF的机器人采集15～20张用于手眼标定的图片可以达到较好的标定精度，采用更高精度的摄像机模型消除相机的畸变影响可以提高手眼标定的精度。

[1] Wang Ying, Zhang Guanlu, Lang Haoxiang, et al. A modified image-based visual servo controller with hybrid camera configuration for robust robotic grasping[J]. Robotics & Autonomous Systems, 2014, 62(10):1398-1407.

[2] Cai Caixia, SOMANI N, NAIR S, et al. Uncalibrated stereo visual servoing for manipulators using virtual impedance control[C]. International Conference on Control Automation Robotics & Vision. IEEE, 2015:1888-1893.

[3] 陶波, 龚泽宇, 丁汉. 机器人无标定视觉伺服控制研究进展[J]. 力学学报, 2016, 48(4):767-783.

[4] TSAI R Y, LENZ R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J]. IEEE Transactions on Robotics & Automation, 1989, 5(3):345-358.

[5] Zhuang Hanqi, ROTH Z S, SUDHAKAR R. Simultaneous robot/world and tool/flange calibration by solving homogeneous transformation equations of the form AX=YB[J]. IEEE Transactions on Robotics & Automation, 1994,10(4):549-554.

[6] MALM H, HEYDEN A. Simplified intrinsic camera calibration and hand-eye calibration for robot vision[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2003:1037-1043.

[7]王君臣,王田苗,杨艳,等. 非线性最优机器人手眼标定[J]. 西安交通大学学报, 2011, 45(9):15-20.

[8]HELLER J, HENRION D, PAJDLA T. Hand-eye and robot-world calibration by global polynomial optimization[C]. IEEE International Conference on Robotics and Automation. arXiv, 2014:3157-3164.

[9] Mo Yuda, Zou Xiangjun, Ye Min, et al. Hand-eye calibration method based on sylvester equation deformation for lychee harvesting robot[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(4):47-54.