一种改进的频偏估计方法及应用

刘 凯，周渊平

(四川大学 电子信息学院，四川 成都 610000)

0 引言

无线接收机时间定位的方式一般可以分为两类，第一类是利用训练序列进行延迟自相关以锁定峰值位置，进而捕获时间偏移量。早期的诸多文献已经对此类算法进行了相当深入的探索[1-2]，其缺陷在于：自相关运算所产生的相关峰并不是十分尖锐，特别是当传输环境极其恶劣(如衰落严重或信噪比很低)时，很难准确获取时间的起始位置。第二类算法是滑动互相关运算，此方法目标函数的相关峰十分尖锐，易于实现时间的同步，其性能明显优于第一类算法，但是却是以计算复杂度偏高为代价的。文献[3]指出，基于互相关运算的方法有一个致命的缺陷，那就是对于频率偏移十分敏感。

频偏估计也有很多经典的算法，最为直接的方法就是利用FFT运算实现频率偏移的跟踪，文献[4-6]从不同的方面阐述了这种方法。此外，关于频偏估计问题，文献[7]设计了一种时频联合的算法，它用一种简单的复数训练序列，在时域估算出小数频偏，在频域估算出整数频偏。基于FFT的各种算法都有一个缺陷——运算量太大，为了快速实现载波同步，文献[8]通过相位折叠的方法使接收信号的频偏具有周期性规律，实现了快速的载波同步，但是这种方法精度并不高。文献[3]构造了一种特殊的CAZAC训练序列，利用该序列不仅可以实现时间上的同步，同时也能进行载波频率偏移的估计。本文主要工作在于补充并改进文献[3]所述算法，为叙述简洁起见，以“原文”代指文献[3]。原文算法之精髓在于，上述特殊的训练序列会随着频偏产生相应的循环移位，而在接收端通过滑动互相关运算能捕获循环移位的偏移量，将频偏巧妙地转换成了序列在位置上的偏移。

1 频率偏移对基于互相关的时间同步性能的影响

基于互相关的时间同步形式，是将包含训练序列c(k)的接收信号序列r(m)与接收机本地序列c(k)做相关运算：

(1)

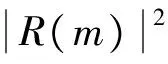
r(m)=c(m-τ)ej2πnω+n(m)

(2)

式中，n(m)为加性噪声。将式(2)代入式(1)得：

(3)

式中假设c(k)c*(k)=1。显然，频率偏移ω将会破坏接收信号中的训练序列与本地序列之间的相关性，削弱相关峰。

图1所示为频偏对式(3)相关峰|R(τ)|的影响，其中相关器长度为127，未考虑噪声因素。

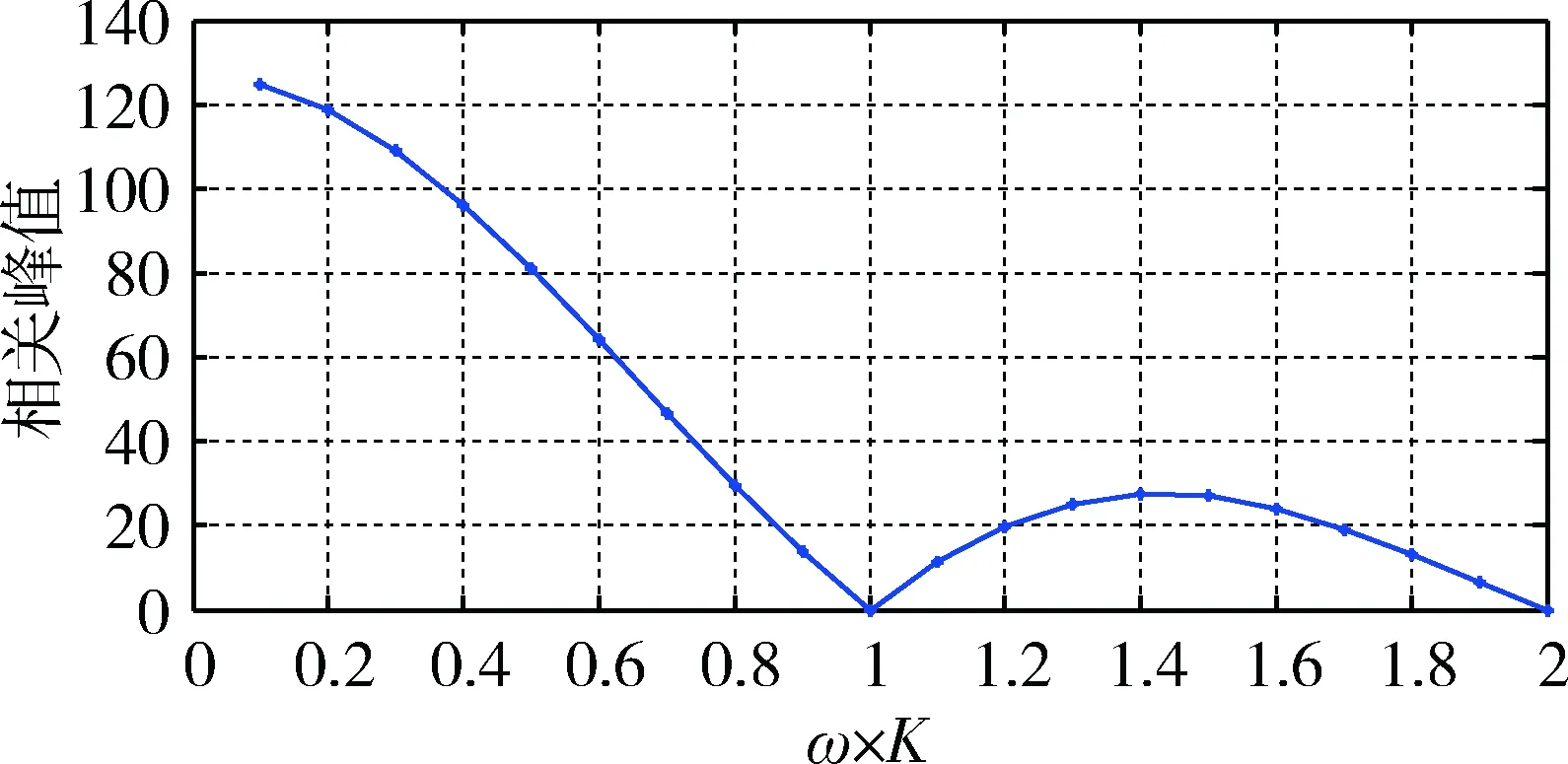
图1 频偏对相关峰值的影响

2 算法基本思想

原文构建了一种长度为L的CAZAC序列：c1=[c1(0)，c1(1)，… ，c1(L-1)]，其中：

(4)

考虑归一化频偏fdTs,这里Ts为采样间隔，fd为频率差值，令:ω=fdTs=(θ+ε)/L，θ∈Z，ε∈[-0.5，+0.5]。其中，θ称为整数频偏，ε称为小数频偏。将接收端带有频偏的离散基带复数信号表示为：

r(k)=c1(k)exp(j2πωk)=

(5)

将式(4)中c1(k)进行循环移位得：

(6)

考察式(6)最后一个因子exp(jπ(L-1)θ2/L)，由于θ2是整数，因此有：

(7)

忽略正负符号上的差异以及式(5)中ε带来的影响，则:

r(k)=c1(k-θ)

(8)

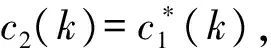
图2 整数频偏对训练序列的影响

考虑情况1，在接收端将收到的信号与本地序列c1进行滑动互相关，目标函数：

(9)

式中，r(m)=[r(m)，r(m+1)，…，r(m+L-1)]，分母的作用是对能量进行归一化。式(9)即可检索出c1的起始位置m1，显然考虑时间延迟量有：

m1=τ1+θ

(10)

用同样的方法即可检索出c2的起始位置m2，依然考虑时间延迟量有：

m2=τ2+L-θ

(11)

由式(10)或式(11)得

(12)

或

(13)

另一方面，联立式(10)和式(11)亦可以求出时间延迟量τ1、τ2，由于训练序列本身就是由重复的序列组成的，那么就可以用延迟自相关求幅角的方式确定ε：

(14)

最终由θ和ε求出载波频偏ω。据此可以实现对含有频偏的接收信号进行补偿。考虑到篇幅限制，此处不再赘述。

3 分析研究与改进

3.1 扩大频偏估计范围

原文指明此算法对于θ的估测范围是[-L/4+1,L/4-1]，而本文经过论证分析，将估测范围推广至[-L/2+1,L/2-1]。

从图2中情况1、2可得，当θ为正整数时，

Δm=m2-m1=3L-2θ

(15)

当θ为负整数时，

Δ′m=m2-m1=L-2θ

(16)

实际应用中在接收端并不会事先知道θ的正负情况，因此无法直接利用式(12)或式(13)求解θ。一般地，只能利用两个相关峰的差值Δm，基于这个原因，在实际应用中就必须保证图2中两种情况下Δm的值域是不同的，即考虑通过Δm的范围来确定频偏的正负情况。原文提到θ∈[-L/4+1,L/4-1],则由式(15)、(16)得：

2.5L<Δm<3L，θ>0

(17)

或

L<Δ′m<1.5L,θ<0

(18)

本文进一步分析了上述两种情形，发现只要保证Δm>Δ′m就能满足互斥条件，综合式(15)、(16)，当满足：

3L-2|θ|>L+2|θ|

即：

(19)

将θ∈[-L/2+1,L/2-1]代入式(15)、(16)中，得θ为正时，

2L<Δm<3L

(20)

而θ为负时，

L<Δ′m<2L

(21)

结论：当θ∈[-L/2+1,L/2-1]时，依然可以通过Δm的值域判定θ的正负情况，结合式(12)、(13)可求解出θ值。

3.2 考虑θ=0的特殊情况

原文虽指出θ∈[-L/4+1,L/4-1]已包含θ=0的特殊情况，但是并未详细分析该情况下如何利用相关峰位置求解出θ。本文研究发现，当θ=0时，训练序列的相关运算会产生4个相关峰，位置依次排列在τ1、τ1+L、τ2、τ2+L处。原文指出在检索出m1之后应在(m1+0.5L，m1+3.5L)范围内检索m2，此时若以第一个相关峰的位置作为m2，则有：

Δm=m2-m1=τ2-τ1=2L

(22)

式(22)表明在进行算法实现时应当考虑Δm=2L的特殊情况，一旦出现就可以锁定θ=0。

3.3 根据给定误差范围选取训练序列周期L

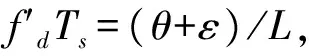
(23)

Δf≤λ

(24)

此处考虑最坏的一种情形，即当fdTs对应的θ理论值并不是整数时，假设此时θ=k+1/2，k是整数。根据式(12)或(13)求出的θ值将可能是k，也可能是k+1，这种情形可以认为误差最大，且误差Δf=1/(2TsL)。于是：

即：

(25)

式(25)指出了实际应用中为满足误差精度要求条件下的训练序列的长度的下限值。

4 性能仿真

基于AWGN信道，针对不同的频率偏移量fd进行仿真实验，根据采样定理，忽略原始基带信号本身的带宽，实际应用中需保证带有频偏的基带信号最高频率(大频偏时约等于频偏值)小于采样频率的一半，在此范围内的任意大小的频率偏移均可以由上述改进后的算法估算出来。此外图3还进行了几组对比实验，研究了不同信噪比下的估计性能。

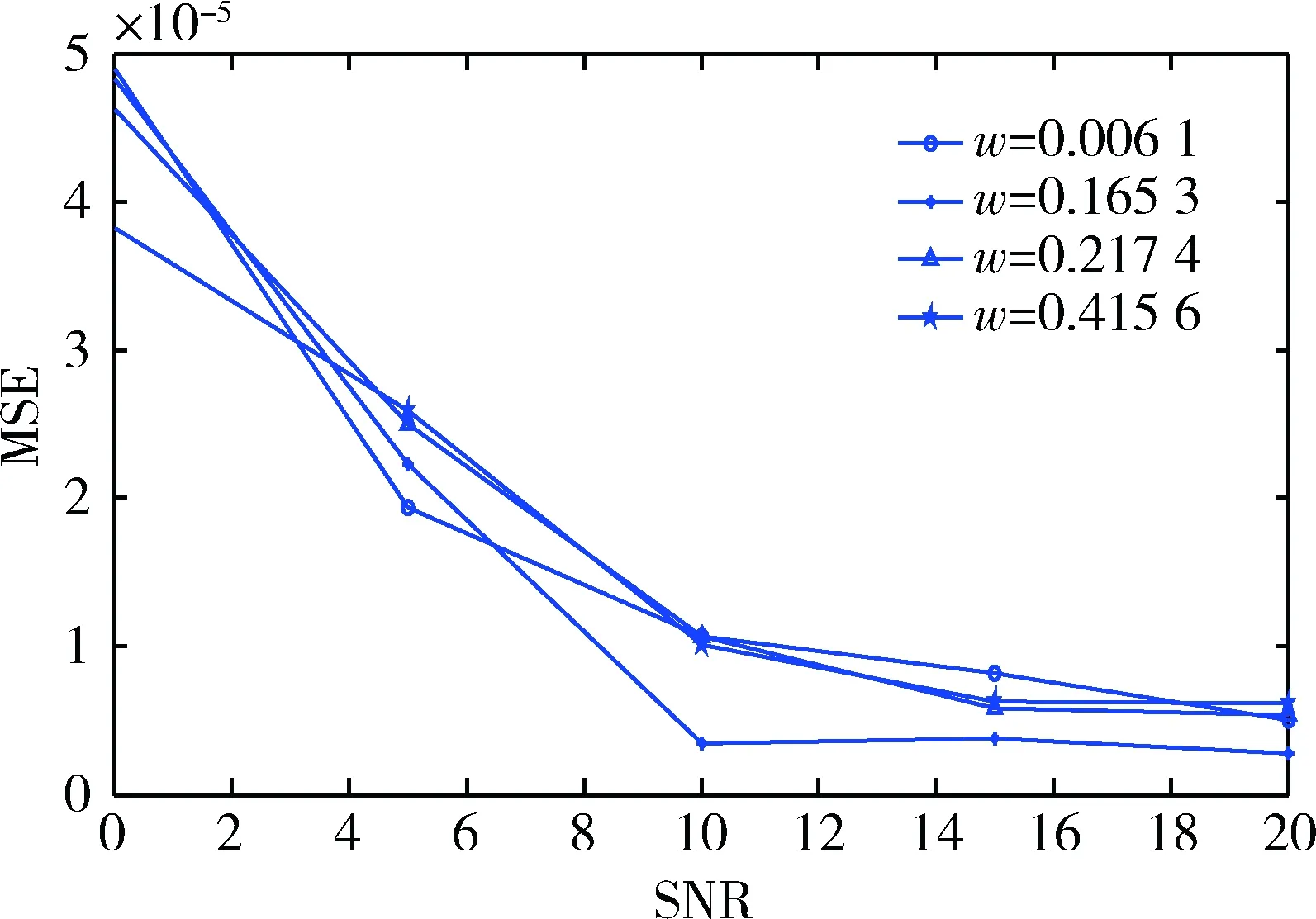
图3 不同信噪比下的估计性能

根据文献[3]所述，算法估计的范围不可能超过0.25，显然通过进一步研究可以实现更为广范围(上限值为0.5)的频偏估计。此外，可以看出，信噪比越高，则频偏估计越准确、性能越好。

5 实践与应用

5.1 实验测试平台简介

本实验基于Zedboard+AD9361实验平台。该开发板搭载了双ARM Cores-A9 处理系统和85 000个7系列可编程单元。Zynq-7000 可以为板上许多应用提供支持。Zedboard实验开发板由多路复用读/写口(Multiplexed I/O, MIO)、可编程逻辑单元(Programmable Logic,PL)、处理系统三大模块构成。

射频部分采用的是AD9361，如图4所示。AD9361射频模块的参数可通过SPI进行配置，主要模块的具体性能如下：

(1)收发天线数：AD9361支持集成的12位DAC和ADC的射频2×2收发器。

(2)收发频率范围：AD9361发射天线与接收天线均支持70～6 000 MHz的频率。

图4 AD9361功能图

AD9361射频模块支持2发2收的MIMO通信系统，工作频段被设计为满足4G通信要求，射频主要参数设置见表1。

表1 射频参数配置

5.2 系统模型

基于Zedboard+AD9361实验系统，搭建了一个小型的2发2收的MIMO通信系统，此系统以2.4 GHz为中心载频，射频板的具体参数配置如表1所示。发射站有两根天线，其距离为8 cm(注：2.4 GHz载频的波长大致为12 cm，MIMO系统天线间的距离需保证大于半波长(即6 cm)即可)。接收站天线的距离设置与发射站相同。

5.3 测试结果展示

对于频偏估计而言，精度和估计的范围往往是最重要的性能指标[10]。此处为了提高精度，在设计无线帧时有意将训练序列长度设置得较长，取L=500。为验证改进后的频偏估计算法的可靠性并测试系统固有频偏(即振荡器之间的频率误差)，将发射端和接收端的射频都设置为2.4 GHz。在发射端先发射一个探测信号：

sg(t)=exp(j2πfg)

(26)

其中，fg=2 MHz，然后在接收端对收到的含有固有频偏的导频信号应用改进后的算法进行频偏估计，利用MATLAB工具对含有固有频偏的导频信号进行频谱分析，整理得到频偏估计值曲线和频谱图如图5、图6所示。

图5 探测信号频谱对比

图6 探测信号频谱峰值位移对比

通过计算，实线相对于虚线峰值移动了12.188 kHz，也就说明固有频偏为12.188 kHz，由表1知基带采样率为30.72 MHz，换算可得系统频偏归一化值为0.000 396。与此同时，采用算法估测的估计值如图7所示。

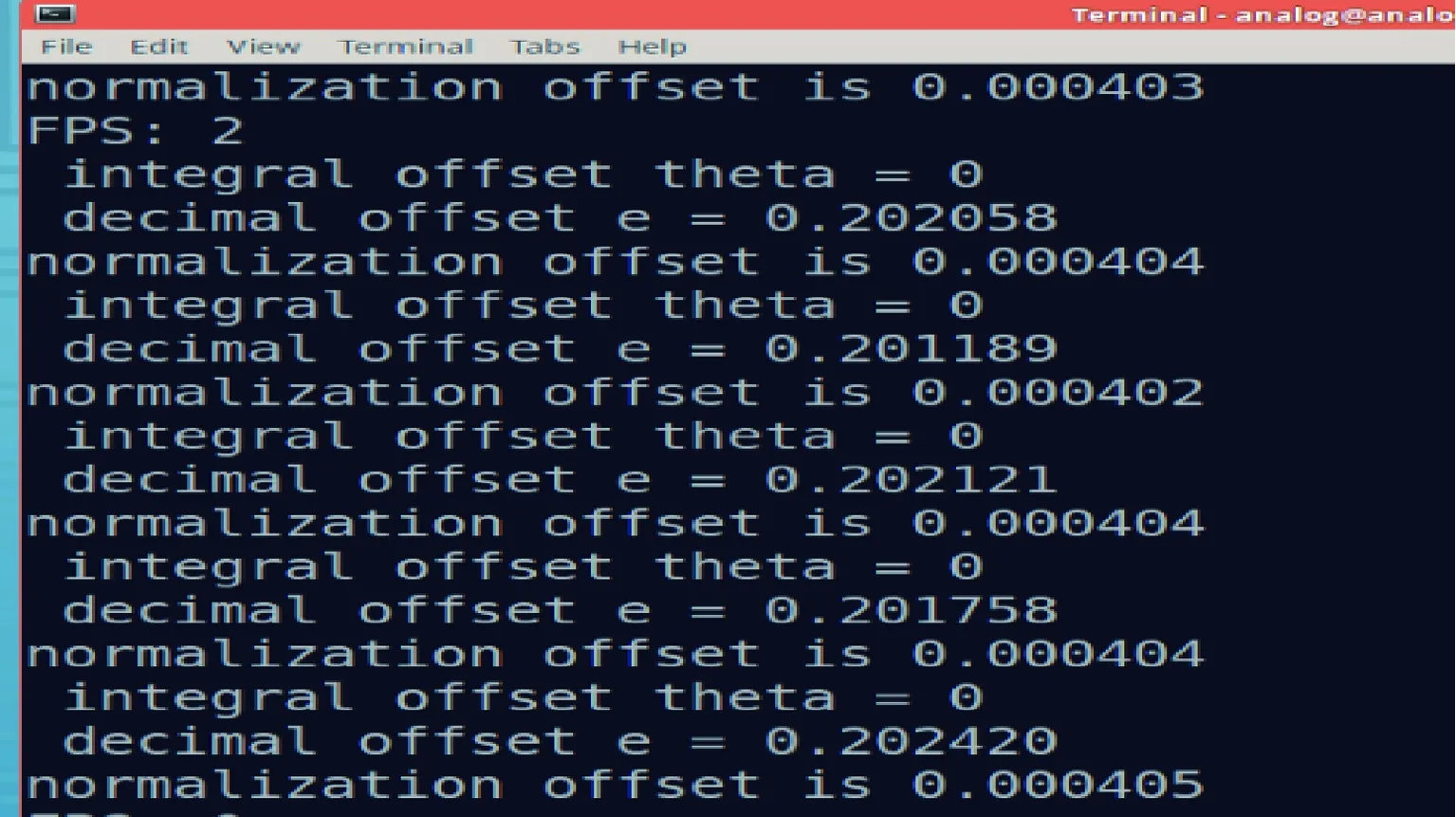
图7 系统固有频偏实时估测

考虑振荡器频率本身会有一定的抖动性(尽管通常这种抖动可以忽略不计)，将实时估测值写入终端，从图7可以看出，归一化频偏估计值为0.000 403，与理论系统频偏值(0.000 396)的方差小于10-10，考虑到误差的存在，可以认为算法是可靠的。因此可进一步研究在不同的频偏下该算法的性能。

保持接收端解调频率为2.4 GHz不变，人为调整发射载频，即设置一些确定的频偏值，然后将实时的估测值与设计的理论值(已含有系统固有频偏)进行对比(见表2)。从表中可以看出，估计值与理论值之间的方差均小于10-9。此外，表中最后一组数据很有意义，其说明了该算法可以估计范围超过0.25的归一化频偏范围。

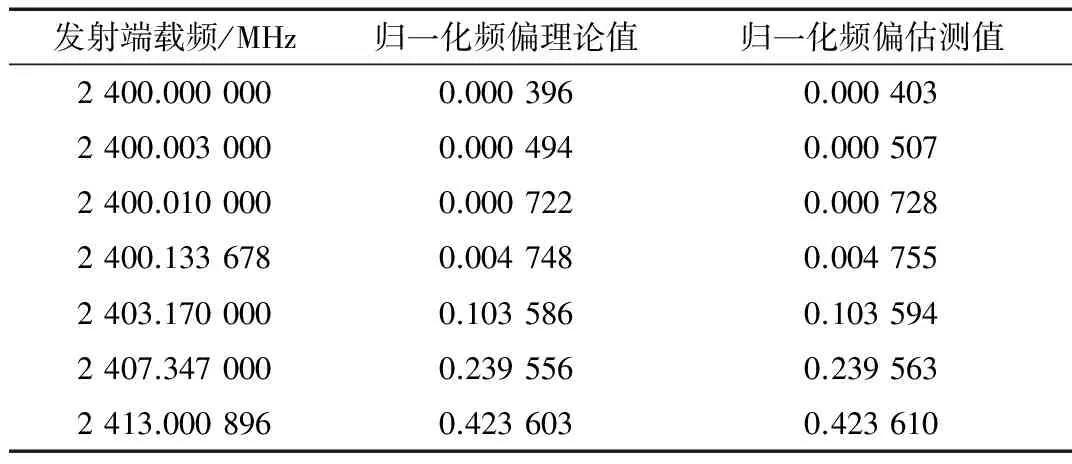
表2 测试结果与理论值

6 结论

通过进一步的研究，将文献[3]关于大频偏下的时间频率同步方法所述的频率估测范围进行了扩展，使得该方法可以胜任更大范围(以采样频率的一半为上限值，即归一化频偏值0.5)的频偏估计，同时，给出了详细的仿真。最后，将改进后的算法应用于实际的MIMO传输环境中，测试数据表明，该方法确实可以解决实际应用中的频率同步问题，并且在存在很大的频偏时依然适用。

[1] Ruan Ming, REED M C, Shi Zhenning. Training symbol based coarse timing synchronization in OFDM systems[J]. IEEE Transactions on Wireless Communications, 2009, 8(5):2558-2569.

[2] TIAN S, PANTA K, SURAWEERA H A, et al. A novel timing synchronization method for ACO-OFDM-based optical wireless communications[J]. IEEE Transactions on Wireless Communications, 2008, 7(12): 4958-4967.

[3] 田园,雷霞,肖悦,等. 存在大频偏时的时间频率同步方法[J]. 电子科技大学学报,2012,41(2):212-216.

[4] 肖丽萍,赵静. 电力线OFDM系统整数频偏估计算法[J].中国电机工程学报，2014,34(19)：3234-3239.

[5] 周新力,龚岳洲,孙小东,等.一种低复杂度的频偏估计算法[J]. 计算机工程,2013,39(3):128-131,145.

[6] 刘毓,邓晓昺.OFDM系统中一种改进的频偏估计算法[J]. 西安邮电大学学报,2013,18(2):62-65.

[7] 姚国义,李鑫,兰瑞田. 一种突发通信信号检测与频偏估计算法[J]. 无线电通信技术,2014，40(4):22-23,41.

[8] 彭刚,杨春兰. 一种改进的频偏估计算法及其性能仿真[J]. 计算机与数字工程,2014,42(2):193-196,222.

[9] 朱乾坤,许阳,刘东鑫,等. 一种基于DFT的高精度载波频偏估计算法[J]. 海军航空工程学院学报,2014,29(4):329-334.

[10] 向劲松,刘飞,马圣明,等. 改进的16QAM载波频偏估计算法[J]. 电视技术,2013,37(15):156-158.