基于外壁监测数据的焦炭塔内壁应力推算方法①

叶伟文 宁志华 汪文锋 刘人怀 王 璠

(1. 广州特种承压设备检测研究院；2. 暨南大学力学与建筑工程学院 “重大工程灾害与控制”教育部重点实验室)

焦炭塔是延迟焦化工艺中的关键设备，在运行过程中经历循环的升温、降温，同时容器承载的介质由气态到液态至固态。焦炭塔的塔壁在经历若干循环后容易出现鼓胀、开裂等问题。根据美国石油协会(API)对焦炭塔进行的4次大规模调查(1968、1980、1998和2016年)的数据显示，许多裂纹是从塔内壁开始萌生的[1～4]，因此内壁应力数据对于焦炭塔的疲劳分析和安全评估而言是极其重要的。

诸多研究者对焦炭塔的应力计算进行了研究[5～13]。文献[5，6]分别对焦炭塔的堵焦阀接管部位和法兰的应力进行了分析计算，结果表明这些部位的应力约为十几至几十兆帕，与塔壁应力相比要小得多。文献[7～10]根据操作参数，采用有限元方法对焦炭塔进油和进水冷却阶段的热弹性场进行了模拟，并对内外壁的应力进行了分析。其中，陈孙艺基于数值分析的温度场数据计算了焦炭塔内外壁的应力，计算结果表明，在进油和进水冷焦阶段由轴向温差引起的内壁最大轴向应力数值可达外壁最大轴向应力的6～8倍[8]。侯春宇等则基于热弹性理论，对焦炭塔的温度场和热弹性应力进行理论分析，同时考虑了径向膨胀对热应力的影响，认为在预热、进油和冷却期间由壁厚方向温差引起的热应力可分别达到138.0、44.8、122.0MPa[11]。谈永明和邵东亮对焦炭塔裙座与筒体连接区域在机械载荷(包括压力、重力和截止静压力)作用下的应力进行了有限元数值模拟，分析结果表明焦炭塔内的机械应力幅值并不大，远低于其屈服强度”[12]。李国成等采用有限元安定分析方法对焦炭塔进行安定分析，同样发现焦炭塔的组合应力中，热应力占主要成分，影响较大。由此可见，焦炭塔的高值应力主要是热应力，且内壁热应力数值有可能比外壁热应力更高[13]。

另一方面，现场实测的应力数据表明[2]，尽管循环工艺和操作参数是固定的，但焦炭塔塔壁的循环应力幅值每个循环都不尽相同，有的应力超过屈服极限，有的则比较低。有学者认为这是由于操作工艺的变化引起内壁附近流体通道情况的变化而导致的[14，15]，而有限元模拟或理论分析很难描述这一现象。因此，利用实时监测的外壁温度和应力数据对焦炭塔内壁应力进行推算，是一种较为合理的方法。文献[16，17]根据塔壁径向温差、轴向温差和周向温差及塔自重、内压等数据，对塔内/外壁应力进行估算，其中为得到径向温差，需要在塔壁向内凿孔至20mm处深埋热电偶去对温度进行测量，再基于温差沿厚度线性分布的假设，推断出内外壁的径向温差。该方法会对塔体产生一定程度的损伤。

由于塔壁应力随着循环而改变，要获得焦炭塔的真实应力数据，必须进行现场实测。而塔内充满了介质，要对内壁应力进行测量非常困难。在焦炭塔的现场实测中，一般是通过在塔外壁安装耐高温应变片和热电偶来获得外壁测点的应变和温度数据。因此，笔者基于热弹性理论和叠加原理，提出一种利用外壁监测得到的温度和应力数据来对内壁应力进行推算的方法，并利用数值分析对计算结果进行了验证。

1 径向温差引起的热应力计算

焦炭塔塔壁的弹性应力主要由内外壁温差和轴向温差两种因素引起。在这一节中，首先分析径向温差引起的热应力。

1.1 方法描述

焦炭塔可视作薄壁圆筒，根据经典薄壳理论，焦炭塔的外壁应力通常可根据监测得到的应变计算公式获得[18]：

(1)

其中，εzo,εθo和σzo,σθo分别为外壁轴向和环向应变和应力分量，下标z,θ分别代表轴向和环向；E为弹性模量，μ为泊松比。

根据弹性力学的热应力分析公式[19]，对于从内部加热/冷却的薄壁圆筒，可推导出其瞬态热应力计算式如下：

(2)

(3)

式中A——热扩散率；

Ri——焦炭塔的内半径；

Ro——焦炭塔的外半径；

α——材料的线膨胀系数；

σTi——内壁的热应力；

σTo——外壁的热应力；

如果塔壁不存在轴向温差，环向应力仅由内外壁温差引起的热应力构成，则：

σθo=σTo,σθi=σTi

(4)

式中σθi——内壁环向应力。

由式(3)得到的温度变化率的计算式为：

(5)

σVo=σZo-σθo

(6)

其中，σVo为外壁轴向应力中瓶颈效应产生的应力分量。由于内外壁的弯曲应力数值相等，正负相反，因此内壁轴向应力可表示为：

σZi=σθi+σVi=σTi-σVo

(7)

式中σZi——内壁轴向应力；

σVi——内壁轴向应力中瓶颈效应产生的应力分量。

1.2 有限元模拟验证

上述方法直接根据监测得到的外壁应力来推算内外壁径向温差引起的内壁应力。以往的方法中，需要从外壁向内钻孔到约20mm深处去埋藏热电偶测温，以此来推算内外壁温差，进而推算径向温差引起的内壁应力[16，17，20]。笔者提出的方法避免了这一举措。

下面采用有限元分析对上述计算方法进行数值验证。考虑一个两端开口的薄壁圆筒，初始整体处于330℃均匀温度场，然后将内壁直接冷却到240℃，分析其瞬态温度场和热弹性场。

采用Ansys公司的Workbench14.5进行数值模拟，薄壁圆筒高度为10m，其他几何参数和材料参数如下：

内半径Ri4.8m

外半径Ro4.83m

弹性模量E204GPa

泊松比 0.284

密度 7 880kg/m3

热扩散系数A1.214×10-5m2/s

线膨胀系数 1.453×10-5/K

比热 460J/kg·K

其中内外半径数值与目前通用焦炭塔的尺寸相同，材料参数与室温下15CrMo的热弹性参数一致。在所假设的温变下，筒壁温度变化较大，其材料参数随温度会发生变化，对热应力的计算结果也有影响。由于此处只是为了对理论方法进行验证，为简便起见，模拟过程中假设材料参数不随温度变化。圆筒外壁绝热，一端固定一端自由。温度场与热弹性场的耦合分析采用间接耦合的方式，采取的时间步长为0.1s。图1为圆筒的网格划分，整个模型单元数目为150 971，节点数目为1 056 827。热分析采用Solid90单元，结构分析采用Solid186单元。

图1 圆筒的网格划分

为避免边缘效应，选取圆筒的中部截面(距离端部5m处)进行考察。图2为筒壁的径向温度分布云图。图3、4分别为该截面的环向应力和轴向应力云图。需要说明的是，图中环向应力和轴向应力的最大值发生在固定端。为对理论方法进行验证，选取圆筒中部截面的应力和温度数据进行计算，得到的结果见表1。

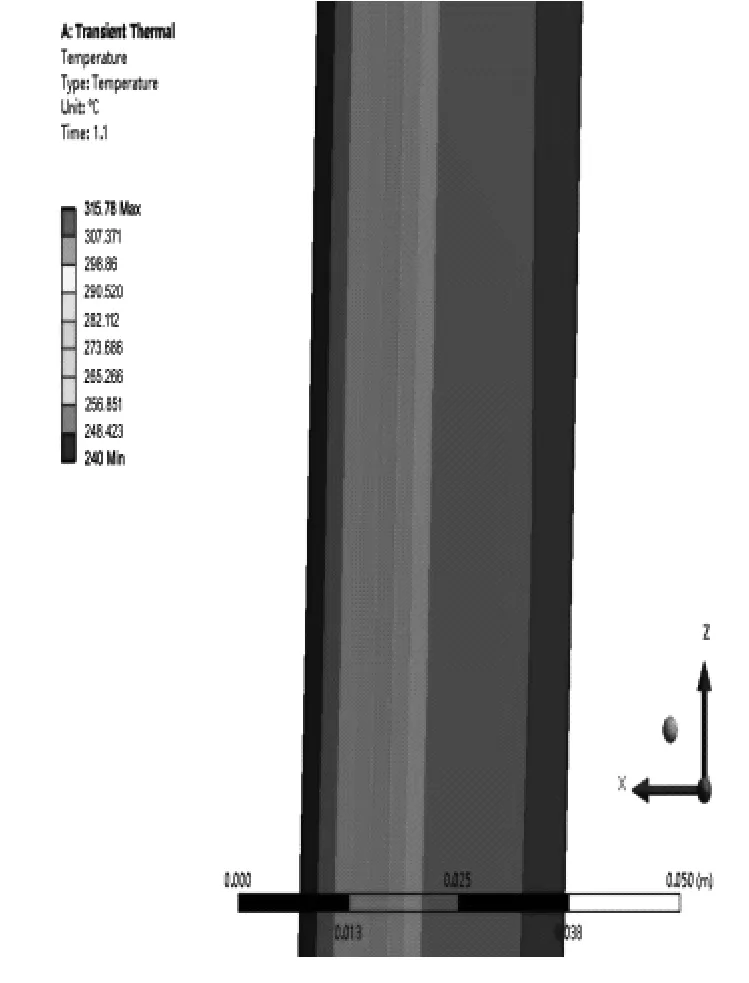
图2 筒壁沿径向的温度分布云图

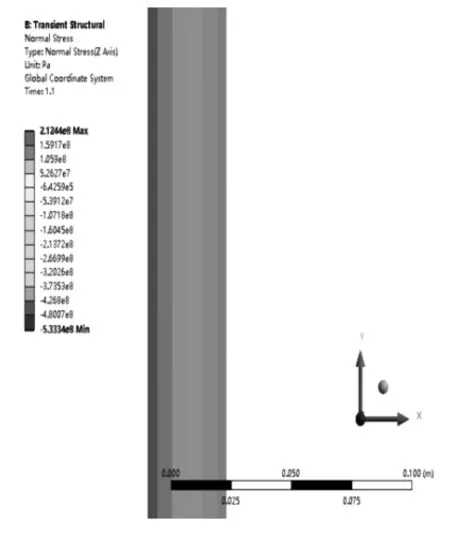
图3 环向应力云图

图4 轴向应力云图

时间sσZoσθoσθiσZi有限元结果MPa有限元结果MPa有限元结果MPa理论结果MPa相对误差%有限元结果MPa理论结果MPa相对误差%1.1-73.53-87.10175.78174.080.97164.71160.502.101.2-74.28-89.30173.51179.00-3.16163.95164.00-0.031.3-74.97-89.64173.66180.00-3.65163.25165.31-1.261.4-74.87-89.17173.57179.00-3.13163.35164.70-0.80

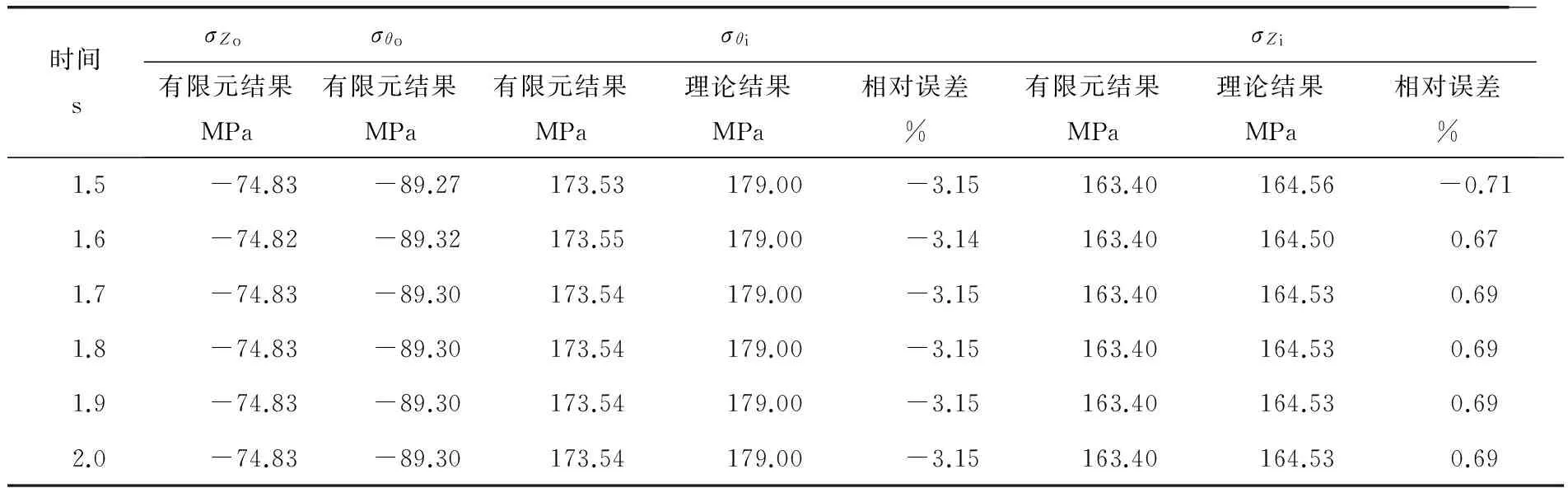
(续表1)

表1的数据是从1.1～2.0s这一时间段选取的，其中内壁应力的理论结果是根据有限元结果的外壁应力σθo与σZo，利用式(2)～(7)进行计算得到的。另外，表中相对误差的计算表达式如下：

(8)

由表中数据易见，利用上述方法对内壁应力的计算比较精确，最大误差不超过3.7%。尤其是对内壁轴向应力σZi的推算，最大误差小于2.1%。由此可见，对于径向温差引起的热应力，采用上述方法根据外壁应力对内壁应力进行推算是合理可行的。

2 轴向温差引起局部热收缩对应力的影响

在焦炭塔的循环过程中，由于介质(热油或冷却水)在塔内沿高度逐步上升，塔壁存在轴向温差，塔壁产生热收缩。而轴向温差引起的局部热收缩会产生轴向的瓶颈效应，尤其在液面附近的塔壁。例如在进水冷却阶段，在冷水进入塔体前，塔壁温度接近330℃，冷水水温为70℃左右。当冷水上升到某个高度，液面上方不远处的塔壁仍保持初始温度，而液面下方的塔壁温度已接近水温，如图5所示。

a. 轴向瓶颈效应示意图

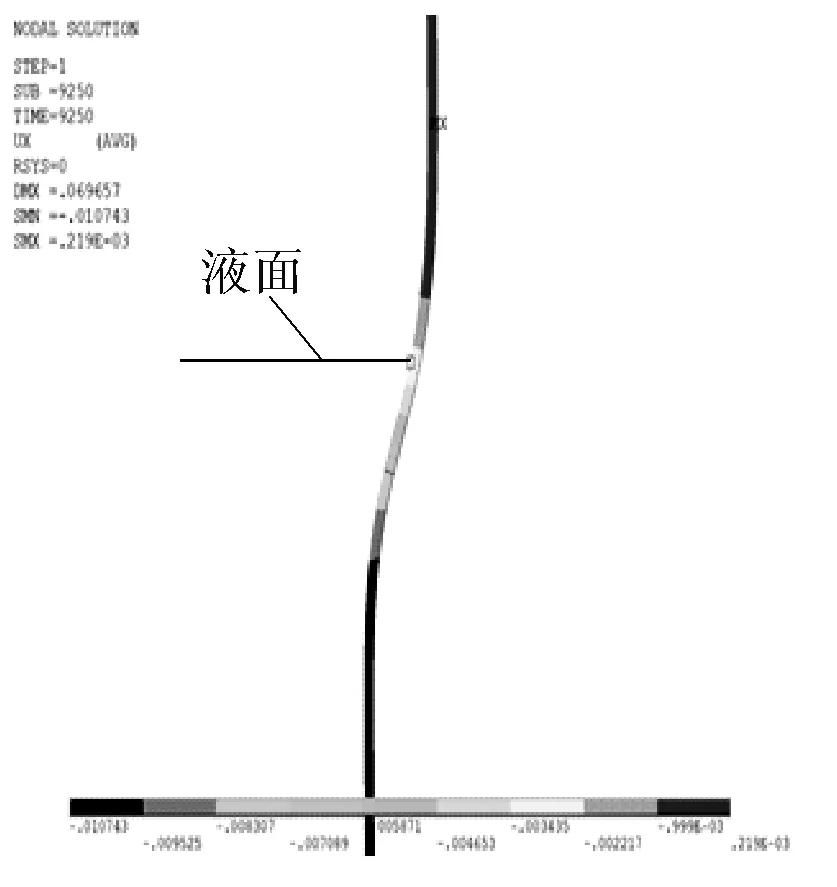
b. 有限元模拟液面附近的塔体

当轴向瓶颈效应通过某一点时，环向应力的产生应包含两方面：径向温差产生的热应力分量和轴向温差引起局部热收缩产生的应力分量。因此，外壁环向应力σθo可写为：

σθo=σTo+EαΔT

(9)

其中σTo为外壁热应力，由式(3)计算；EαΔT为局部热收缩，ΔT是瓶颈效应发生瞬间相邻两部分的温差，ΔT=T2-T1，T2为进油或进水前塔壁的初始温度，T1为液体与塔壁之间热传导完成后塔壁的温度。

文献[21]认为，虽然瓶颈效应通过某个点是瞬间发生的，但由此引起的热收缩并非瞬时就达到最大程度，而是与过渡长度lt成比例，如图6所示。由于过渡长度lt的确定比较复杂，需要进一步的分析，并且lt会随着循环的不同而改变。因此，他们认为从统计平均的角度出发，可将式(9)改写为σθo=σTo+βEαΔT(0≤β≤1)，β需要通过统计分析获得。

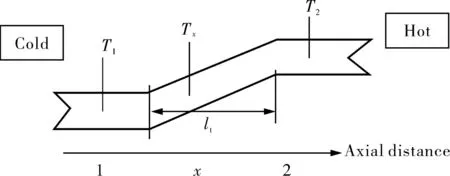
图6 瓶颈效应的过渡长度

笔者认为，瓶颈效应引起的瞬时热收缩应该与该点的瞬时温度有关系，计算环向应力时应采用该点的瞬时温变，因此式(9)应改写为：

σθo=σTo+EαΔTx

(10)

其中ΔTx为计算点的瞬时温变，ΔTx=Tx-T2，此处Tx为计算点的瞬时温度。

3 焦炭对塔壁应力的影响

根据Ellis P J和Hardin E E的测量发现，生焦的热膨胀系数高于焦炭塔塔壁的热膨胀系数[14]。他们认为，如果缓慢、均匀地冷却焦炭和塔壁，则在塔壁中不会出现向外的压力；但如果塔壁的冷却速度比焦炭快，则塔壁就会受到焦炭的压力，从而可能导致塔体的鼓胀。另有测试表明[15]，在焦炭塔中的焦炭实际上并非多孔性，仅在靠近塔壁处孔隙稍微多些，因而当水冷却速率过高时，冷水就会流进焦床的外围去冷却塔壁。这一说法能很好地解释急冷时塔体鼓胀的现象。因此在水冷阶段，塔壁应力的计算中应考虑来自固体焦炭的压力作用。固体焦炭的压力对塔壁应力的贡献应与内压类似，但焦炭的压力是由于某处塔壁附近局部焦炭的多孔性导致冷水直接接触塔壁，使得塔壁收缩而受到焦炭的挤压。因此两者的作用是有差别的，塔内气体产生的内压是均匀作用在塔壁上的，而焦炭对塔壁的压力是局部的，且难以判断压力的位置和大小。如果在塔壁应力的计算中要计及焦炭的影响，还需要对这方面进行更多的了解和深入的研究。

根据Ellis P J和 Paul C A提供的测试数据，针状焦的横向热膨胀系数为15.4×10-6/℃，而塔壁的热膨胀系数为1.20×10-6/℃，如果是海绵胶，则具有更高的热膨胀系数[15]。值得注意的是，文献[22，23]给出的焦炭热膨胀系数仅为3.00×10-6/℃，而塔壁的热膨胀系数数值介于11.90×10-6～14.06×10-6/℃之间(与温度相关)，由此认为焦床的收缩相较塔壁而言要小得多，因此焦床对塔壁产生了显著的套合压力。

以上国内外学者给出两种截然相反的观点，其矛盾的焦点在于焦炭与塔壁的热膨胀系数孰高孰低。因此，需要对焦炭的热膨胀系数进行更为可靠的测试，焦床对塔壁应力的影响还有待进一步的考察。

4 内壁应力推算方法

综合上述各种因素的影响，焦炭塔内壁的应力可利用外壁监测的应力和温度数据按如下方法进行推算。

内壁径向温差引起的热应力为：

(11)

其中σθ*为内压(包括气压和焦炭产生的压力)在塔壁产生的环向应力分量。内壁环向应力为：

σθi=σTi+βEαΔTx+σθ*

(12)

内壁轴向应力为：

σZi=σTi+σZ*-(σZo-σθo)

(13)

其中σZ*为内压(包括气压和焦炭产生的压力)在塔壁产生的轴向应力分量。

根据焦炭塔的工况，某个截面瓶颈效应主要发生在进油和水冷阶段，当液面通过该截面的瞬间。在蒸汽预热或油气预热阶段，轴向温差很小，相应的瓶颈效应也很小。因此采用上述方法对内壁应力进行推算时，并不需要判断轴向瓶颈效应是否发生。故上述方法既可引入到在线监测系统的应力计算中，也可考虑应用于后续焦炭塔的疲劳分析，如对内壁裂纹萌生和裂纹扩展的应力/应变计算中。

5 结论

5.1理论计算结果与有限元数值模拟结果对比表明，笔者提出的计算方法对于内部加热或冷却引起径向温差产生的热应力推算精度较高。

5.2在焦炭塔的进油或水冷阶段，由于塔壁存在严重的轴向温度梯度，因此内壁环向应力的计算应考虑局部热收缩产生的贡献。

5.3在冷焦阶段，焦床对塔壁应力的影响取决于焦炭与塔壁材料热膨胀系数的大小。如果焦炭的热膨胀系数高于塔壁材料，只有当冷却速率过高，使得冷水流至焦床外围直接冷却塔壁，才会导致焦炭对塔壁产生的挤压作用。如果焦炭的热膨胀系数低于塔壁，焦床的收缩相较塔壁而言要小，则焦床将对塔壁产生了显著的套合压力。目前，国内外学者在这方面的观点存在分歧，因此焦炭对塔壁应力的贡献还需要更多的调查数据和进一步深入的研究。

[1] Thomas J W.API Survey of Coke Drum Cracking Experience[C].Proceeding of American Petroleum Institute，Refineries Department.Cleveland.Ohio：Stand Oil Company，1981：141～153.

[2] BagdasarianA，Horwege J，Kirk S，et al.Integrity of Coke Drums(Summary of 1998 API Coke Drum Survey)[J].Pressure Vesselsand Piping Division(Publication)，Service Experience and Fitness-for-Service in Power and Petroleum Processing，ASME，2000，411：265～270.

[3] American Petroleum Institute. Design，Fabrication，Operational Effects，Inspection，Assessment，and Repair of Coke Drums and Peripheral Components in Delayed Coking Units[R]. API Technical Report 934-G，2016.

[4] 陈晓玲，段滋华，李多民.国内外焦炭塔的研究现状及其进展[J].化工机械，2009，36(1)：56～59.

[5] 王庆华，黄振仁，成建国，等.焦炭塔堵焦阀接管部位的应力计算及高温应力测试[J].化工机械，1996，23(4)：216～220.

[6] 史雨竹，王伟.焦炭塔法兰应力分析计算[J].化工机械，2013，40(2)：170～171，241.

[7] 陈孙艺，林建鸿，吴东棣，等.焦炭塔塔壁温度场特性的研究(一)——塔壁二维瞬态温度场及热弹塑性有限元计算分析[J].压力容器，2001，18(4)：16～21.

[8] 陈孙艺.焦炭塔的三维温度场及其应力分析[J].石油化工设备技术，1997，18(1)：5～10.

[9] 宋晓江，王春生，宣培传，等.焦炭塔温度场及热应力场的有限元计算[J].石油化工设备，2007，36(2)：28～32.

[10] 李国成，王为良，李荣生.焦炭塔瞬态温度场及热应力分析[J].压力容器，2010，27(9)：21～25，37.

[11] 侯春宇，韩放，王莉.焦炭塔热应力的推导计算[J].化工装备技术，2009，30(5)：38～39.

[12] 谈永明，邵东亮.焦炭塔裙座与筒体连接区域应力分析[J].化工机械，2011，38(4)：457～460，495.

[13] 李国成，张文，吴娜.焦炭塔热机棘轮效应的安定性分析[J].化工机械，2010，37(4)：444～446.

[14] Ellis P J，Hardin E E.How Petroleum Delayed CokeForms in a Drum[C].Light Metals 1993.Pittsburgh：The Minerals，Metals and Materials Society，1993：509～515.

[15] Ellis P J，Paul C A.Delayed Coking Fundamentals[C].AICHE Spring National Meeting.New Orleans：American Institute of Chemical Engineers，1998：67～68.

[16] 荣晓瑞.焦炭塔筒体热应力的理论分析[J].炼油与化工，2010，21(3)：25～27.

[17] 李一玮.延迟焦化装置焦碳塔的变形、开裂机理和安全分析[J].压力容器，1987，4(4)：61～66.

[18] 韩强，黄小清，宁建国.高等板壳理论[M].北京：科学出版社，2002.

[19] 程昌钧，朱媛媛.弹性力学[M].上海：上海大学出版社，2005.

[20] 金志英，王岫文，马燕文，等.焦碳塔的鼓胀、裂纹容限及寿命预测[J].压力容器，1993，10(2)：67～72.

[21] Church J M，Lim L B，Brear J M，et al.Crack Growth Modelling and Probabilistic Life Assessment of Coke Drums Operating under Fatigue Conditions[J].International Journal of Pressure Vessels & Piping，2001，78(11/12)：1011～1020.

[22] 朱成诚，赵建平.焦炭塔的套盒效应研究[J].压力容器，2016，33(9)：34～41.

[23] 赵莹，周鸿.焦炭塔的鼓凸损伤分析[J].西安石油学院学报，1998，13(6)：38～41.