材料及结构参数对约束阻尼结构阻尼性能的影响

李 辉， 李 斌， 孙国华， 马卫东， 孙志勇， 肖 勇， 杜华太

(中国兵器工业集团 第五三研究所， 山东 济南 250031)

0 引 言

约束阻尼结构因其卓越的耗能减振性能被广泛应用在航空、 航天、 船舶、 汽车、 建筑等领域， 研究人员针对约束阻尼材料、 结构参数设计开展了大量研究．

吕平[1]等以大理石板、 砂浆板为基层研究了阻尼层厚度、 约束层材料、 环境温度对约束阻尼结构阻尼性能的影响， 研究结果表明， 当阻尼层厚度在1～4 mm范围内时， 约束阻尼结构的阻尼性能随阻尼层厚度的增加而降低； 不同材料的约束层， 约束阻尼结构的阻尼性能不同； 常温环境下， 约束阻尼结构的阻尼值较大， 高温、 低温环境阻尼值均较小． 杨青[2]等以尺寸为400 mm×35 mm×2 mm 铝板为研究对象， 针对目前通常采用阻尼材料的损耗因子、 储能模量来评估材料减振性能的方法不能直观有效反映材料在实际应用中减振降噪效果的问题， 采用正弦扫描和随机振动激励激振简支梁的方法， 通过分析响应数据来表征约束阻尼材料的减振降噪效果． 郑成龙[3]采用有限元仿真计算和试验相结合的方式研究了基层尺寸为300 mm×200 mm×2 mm 的钢板、 阻尼层为橡胶、 约束层为铝箔的约束阻尼材料的阻尼性能． 汪浩[4]等以470 mm×320 mm×10 mm的金属板为基层， 研究了阻尼对复合试样共振频率、 结构损耗因子、 减振性能的影响． 研究结果表明， 在阻尼复合试样减振效果测量过程中， 应当注意各次测量时不同激励力的力谱对测量结果可能产生的影响， 通过对基板测量时激励力力谱的归一化来减小减振效果测量误差； 阻尼材料的减振效果存在一个优化的厚度比， 考察不同厚度比条件下复合试样的减振效果可确定优化的厚度比值， 对于阻尼材料结构设计是必要的． 郑荣[5]等以尺寸为800 mm×500 mm×8 mm的钢板为基层， 研究了约束阻尼处理面积、 处理层数等不同处理形式下的减振效果． 结果表明， 阻尼处理面积与处理重量和减振效果无明显关系． 张彩霞[6]采用耦合有限元和间接边界元的方法对约束阻尼层厚度进行了优化设计， 根据声辐射功率和结构表面振动加速度之间的关系， 选取振动加速度的平方和作为目标函数， 以各层厚度和总质量作为设计变量和状态变量， 对某固定的矩形约束阻尼板进行了优化仿真， 并对优化前后的约束阻尼板进行声学响应分析． 结果表明， 约束阻尼层厚度对阻尼减振有确定性的定量影响关系， 优化后的声辐射功率明显降低． 韩俊[7]采用有限元法对敷设约束阻尼封闭箱体的声-固耦合模型进行了声振特性分析， 讨论了约束阻尼的结构参数和敷设位置对箱体结构声振特性的影响， 结果表明， 约束阻尼处理对箱体具有明显的减振降噪作用， 且其结构参数和敷设位置存在最优值．

铝蜂窝板作为一种轻质高刚度的复合材料， 在航空、 车辆等领域被大量应用， 但是将其作为约束层材料用于约束阻尼结构的研究较少， 且现有研究中的基层多为薄板材料， 以厚钢板为基层的研究较少． 本文采用自由板振动法， 以 8.5 mm 厚的钢板为基层， 以橡胶材料为阻尼层， 以铝蜂窝板为约束层， 研究了阻尼层橡胶材料性能、 约束层厚度、 阻尼层厚度等约束阻尼结构参数对阻尼性能的影响．

1 实验部分

1.1 实验材料及仪器设备

钢板， 尺寸为400 mm×300 mm×8.5 mm； 阻尼橡胶(自制)， WSXJ 4162-1, QCZNP 08-5； 铝蜂窝板， 厚度分别为6， 10， 15 mm， 青岛海立泰公司； LMS Test Lab 11B测试软件， 16通道信号采集分析仪， 比利时LMS公司； 加速度传感器， 力锤， 美国PCB公司； 电脑； NETZSCH DMA测试仪； 力学性能试验机； 高低温试验箱； 橡胶真空硫化机等．

1.2 试样

以钢板为基层， 以自制阻尼橡胶为阻尼层， 以轻质、 高刚度的铝蜂窝板为约束层， 设计并制备了约束阻尼试样， 试样结构如图 1 所示， 试样编号及阻尼层、 约束层厚度如表 1 所示， 其中试样①～⑦所用阻尼橡胶为WSXJ 4162-1(简称4162-1)， 试样⑦所用阻尼橡胶为QCZNP 08-5(简称08-5)．

图 1 试样结构示意图Fig.1 Sample structure schematic diagram

试样编号阻尼层厚度/mm约束层厚度/mm①1．66②1．610③1．615④0．810⑤2．410⑥3．210⑦1．610

1.3 性能测试

1.3.1 阻尼性能

使用LMS Test Lab软件、 信号采集分析仪、 加速度传感器、 力锤、 电脑、 高低温试验箱等仪器测试约束阻尼试样在-20， 0， 20， 40 ℃时一阶、 二阶模态的共振频率和结构损耗因子． 测试时， 使用橡胶绳将试样悬挂在高低温试验箱内， 使用快粘胶将加速度传感器粘贴到试样基层表面． 试样安装状态如图 2 所示， 图中对力锤激励点和加速度信号采集点进行了标示．

图 2 试样安装状态及测点布置Fig.2 Sample installation condition and measuring point position

试样安装完成后开始温度调节， 温度调节时间不小于30 min， 温度调节完成后使用力锤敲击试样基层并采集力信号和振动加速度信号， 最后处理采集到的传递函数曲线， 得到共振频率和结构损耗因子． 测试中， 加速度传感器的采样频率为0～2 048 Hz， 精度为0.5 Hz. 结果处理时， 使用3 dB带宽法计算得到试样的结构损耗因子．

1.3.2 阻尼橡胶的阻尼系数和模量

使用NETZSCH DMA测试仪按照标准ASTM D4065-2006的规定测试阻尼层橡胶的模量和阻尼系数， 试样厚度2 mm， 采用剪切模式， 最大振幅80 μm， 最大动态力6 N， 频率3.33 Hz， 测试温度范围-50～60 ℃， 升温速度3 ℃/min．

1.3.3 铝蜂窝板的弯曲刚度

使用力学性能试验机按照标准GB/T 1456-2005的规定测试铝蜂窝的弯曲刚度， 试样长宽尺寸为550 mm×30 mm， 厚度为铝蜂窝板厚度．

2 结果与讨论

2.1 阻尼层橡胶性能的影响

试样②所用橡胶为4162-1， 试样⑦所用橡胶为08-5， 其他结构参数相同， 以试样②和⑦来分析阻尼层橡胶性能对约束阻尼试样阻尼性能的影响. 首先使用DMA测试仪测试了阻尼层橡胶材料4162-1和08-5的阻尼系数和模量， 测试结果如图 3， 图 4 所示．

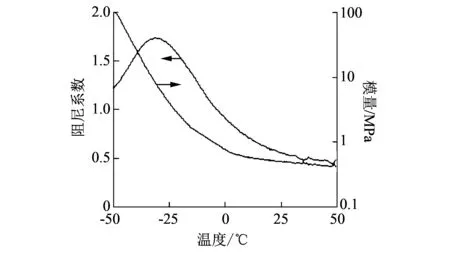
图 3 橡胶4162-1的阻尼系数和模量Fig.3 Damping coefficient and modulus of rubber 4162-1

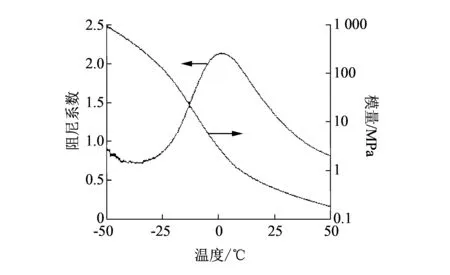
图 4 橡胶08-5的阻尼系数和模量Fig.4 Damping coefficient and modulus of rubber 08-5

图 3与图 4 的测试结果表明， 在-50～60 ℃温度范围内， 橡胶4162-1和08-5的阻尼系数均表现为先增大后降低， 阻尼系数峰值相近， 但是峰值对应温度相差较大， 4162-1对应-32 ℃， 08-5对应1 ℃； 4162-1的模量范围是0.36～113 MPa， 08-5的模量范围是0.14～882 MPa. 在20 ℃以下， 08-5的模量显著高于4162-1， 在20 ℃以上， 4162-1的模量略高于08-5．

图 5 与图 6 分别是约束阻尼试样②和⑦在-20～40 ℃ 温度范围内一阶、 二阶模态的共振频率图和结构损耗因子图．

由图 5 可知， 试样②一阶、 二阶模态的共振频率均低于⑦， 在两件试样其他结构参数相同的情况下， 造成这个现象的原因是阻尼橡胶性能的差异， 即试样②所用橡胶4162-1的模量低于试样⑦所用橡胶08-5的模量． 四周自由薄板共振频率的计算公式如式(1)[8]所示．

(1)

式中：f为共振频率；h为厚度；A为频率常数；a为宽度；E为弹性模量；ρ为密度；μ为泊松比． 由式(1)可知， 增大薄板的弹性模量， 其共振频率将提高， 也可以解释试样⑦的共振频率高于试样②的现象．

图 5 试样②与⑦的共振频率随温度的变化情况Fig.5 Curves of resonance frequency of sample ② and ⑦ vary with temperature

图 6 试样②与⑦的结构损耗因子随温度的变化情况Fig.6 Curves of structure loss factor of sample ② and ⑦ vary with temperature

图 6 中， 因为阻尼层橡胶材料的差异， 试样②与⑦的阻尼性能差异很大， 试样⑦的阻尼温域宽于②， 试样②的结构损耗因子峰值温度处于0～10 ℃ 之间， 试样⑦的结构损耗因子峰值温度大于40 ℃. 与②相比， 试样⑦所用橡胶的阻尼系数峰值温度较高. 试样②的结构损耗因子呈先增大后减小的趋势， 这与4162-1橡胶的阻尼系数变化规律相同， 两者峰值温度的差异主要是由于其结构参数差异导致的. 试样⑦未出现结构损耗因子峰值， 这是因为08-5的阻尼温域偏宽， 导致试样⑦的阻尼温域宽， 在-20～40 ℃温度范围内未出现结构损耗因子峰值．

2.2 约束层厚度的影响

试样①， ②， ③约束层铝蜂窝板的厚度依次为6, 10, 15 mm， 其他结构参数相同， 以试样①， ②， ③来分析约束层厚度对约束阻尼试样阻尼性能的影响． 表 2 为铝蜂窝板的面密度和弯曲刚度．

表 2 铝蜂窝板性能参数表

在-20～40 ℃的温度范围内， 试样①, ②, ③一阶、 二阶模态的共振频率和结构损耗因子测试结果分别如图 7 与图 8 所示．

图 7 试样①, ②, ③的共振频率随温度的变化情况Fig.7 Curves of resonant frequencies of samples ①, ② and ③ vary with temperature

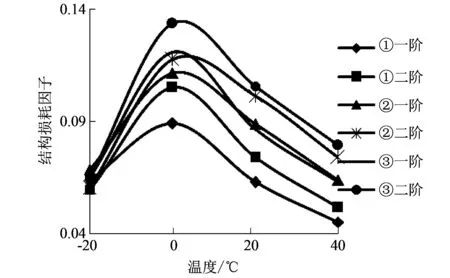
图 8 试样①, ②. ③的结构损耗因子随温度的变化情况Fig.8 Curves of structural loss factors of samples ①, ② and ③ vary with temperature

由图 7 可知， 随着约束层铝蜂窝板厚度的增加， 试样①,②,③的一阶、 二阶模态的共振频率均依次增加． 板的弯曲刚度的计算公式如式(2)[9]所示

(2)

式中：D为弯曲刚度；E为模量；h为厚度；μ为泊松比．

将式(2)代入式(1)得到

(3)

式中：f为共振频率；A为频率常数；a为宽度；D为弯曲刚度；ρ0为面密度．

表 2 中， 随着厚度的增加， 铝蜂窝板的弯曲刚度显著增大， 而面密度变化较小. 根据式(3)可知， 在其他参数不变的条件下， 试样①, ②, ③的共振频率依次增大， 与试验结果相同．

由图 8 可知， 在-20 ℃时， 约束层厚度对试样结构损耗因子的影响不明显. 当温度升高时， 随着约束层厚度的增加， 试样①, ②, ③一阶、 二阶模态的结构损耗因子均呈增大的趋势． 当基层与约束层的厚度和模量相当时， 约束阻尼结构表现出最佳的阻尼性能． 在上述3件试样中， 基层8.5 mm厚钢板的刚度远大于约束层铝蜂窝板的， 因此随着铝蜂窝板厚度的增加其刚度相应增大， 表现在约束阻尼结构中即为结构损耗因子的增大．

2.3 阻尼层厚度的影响

试样④， ②， ⑤， ⑥阻尼层橡胶的厚度依次为0.8， 1.6， 2.4， 3.2 mm， 其他结构参数相同． 以试样④， ②， ⑤， ⑥来分析阻尼层厚度对约束阻尼试样阻尼性能的影响．在-20～40 ℃的温度范围内， 试样④， ②， ⑤， ⑥一阶模态的共振频率和结构损耗因子测试结果分别如图 9 与图 10 所示．

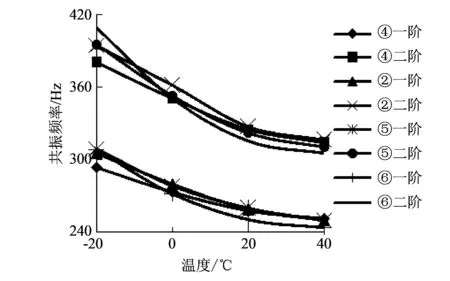
图 9 试样 ④， ②， ⑤， ⑥的共振频率随温度的变化情况Fig.9 Curves of resonant frequencies of samples ④， ②， ⑤， ⑥ vary with temperature

图 9 中， 试样④， ②， ⑤， ⑥的共振频率差异不明显， 可见阻尼层厚度对约束阻尼试样的共振频率影响不明显． 图 10 中， 随着阻尼层厚度的增加， 约束阻尼试样的结构损耗因子总体呈增大的趋势； 试样④， ②， ⑤， ⑥一阶、 二阶模态的结构损耗因子范围分别是0.05～0.11， 0.06～0.12， 0.06～0.14， 0.06～0.16．

约束阻尼结构的结构损耗因子计算公式如式(4)～式(6)[10]所示

(4)

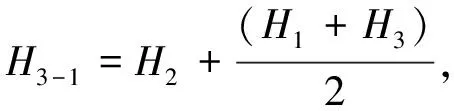
式中：η为结构损耗因子；E1为基层材料模量；E2为阻尼层材料模量；E3为约束层材料模量；H1为基层厚度；H2为阻尼层厚度；H3为约束层厚度；β2为阻尼层阻尼系数；G2为阻尼材料的动态剪切模量；f为振动频率；ρ1为基层密度；g为剪切参数；H3-1为基层与约束层的中心距． 由式(2)～(4)可知， 增加阻尼层厚度， 结构损耗因子将增大， 可以解释上述试验中随着试样④， ②， ⑤， ⑥阻尼层厚度的增加， 其结构损耗因子依次增大的现象．

图 10 试样④， ②， ⑤， ⑥的结构损耗因子随温度的变化情况Fig.10 Curves of structural loss factors for Specimens ④， ②， ⑤， ⑥ vary with temperature

3 结 语

本文以8.5 mm厚钢板为基层， 以橡胶材料为阻尼层， 以铝蜂窝板为约束层， 研究了阻尼橡胶性能、 约束层厚度、 阻尼层厚度等结构参数对约束阻尼试样阻尼性能的影响. 主要结论如下：

1) 阻尼层橡胶材料的性能对约束阻尼试样的共振频率和结构损耗因子均有明显的影响. 共振频率随着橡胶模量的增高而增高， 橡胶材料的阻尼系数峰值温度显著影响约束阻尼试样的结构损耗因子峰值温度． 在约束阻尼结构设计中， 通过调节橡胶材料的有效阻尼温域来设计约束阻尼结构的有效阻尼温域具有显著的效果．

2) 当约束层为厚度6， 10， 15 mm的铝蜂窝板时， 随着约束层厚度的增加， 约束阻尼试样的共振频率和结构损耗因子依次增大. 因此在本文的约束阻尼结构中， 增加约束层铝蜂窝板的厚度有利于提高试样的阻尼性能．

3) 当阻尼层为0.8， 1.6， 2.4， 3.2 mm的橡胶材料时， 阻尼层厚度对约束阻尼试样的共振频率没有明显影响， 对结构损耗因子影响显著. 随着阻尼层厚度增加， 试样的结构损耗因子依次增大． 因此在本文的约束阻尼结构中， 增加阻尼层橡胶的厚度有利于提高试样的阻尼性能．

[1] 吕平， 高金岗， 李晶， 等. 影响约束阻尼结构阻尼性能的因素[J]. 噪声与振动控制， 2014， 34(5)： 234-238.

Lü Ping, Gao Jingang, Li Jing, et al. Impacting factors of damping performance of constraint damping structures[J]. Noise and Vibration Control, 2014, 34(5)： 234-238.(in Chinese)

[2] 杨青， 王新， 张文伟， 等. 约束层阻尼结构降噪性能的测试分析[J]. 噪声与振动控制， 2010(4)： 150-152.

Yang Qing, Wang Xin, Zhang Wenwei, et al. Study on noise suppressing performance of constrained layer damping structure[J]. Noise and Vibration Control, 2010(4)： 150-152.(in Chinese)

[3] 郑成龙. 复合约束阻尼结构动力学特性及其车内降噪应用研究[D]. 长沙： 湖南大学， 2013.

[4] 汪浩， 肖邵予. 阻尼材料减振性能试验研究[J]. 中国舰船研究， 2009， 4(1)： 38-42.

Wang Hao, Xiao Shaoyu. Experimental study on damping properties of acoustical materials[J]. Chinese Journal of Ship Research, 2009, 4(1)： 38-42. (in Chinese)

[5] 郑荣， 姚利锋. 某型扫雷舰主机基座阻尼结构优化研究[J]. 船舶， 2008(2)： 39-44.

Zheng Rong, Yao Lifeng. Damping structure optimization for main engine foundation on a mine sweeper[J]. Ship and Boat, 2008(2)： 39-44.(in Chinese)

[6] 张彩霞， 沙云东， 朱琳， 等. 薄壁结构约束阻尼板减振降噪优化设计[J]. 沈阳航空航天大学学报， 2014， 31(3)： 32-38.

Zhang Caixia, Sha Yundong, Zhu Lin, et al. Optimization design of thin-walled structure with constrained damping layer[J]. Journal of Shenyang Aerospace University, 2014,31(3)： 32-38.(in Chinese)

[7] 韩俊， 向宇， 陆静. 敷设被动约束层阻尼封闭箱体结构声振特性分析[J]. 广西工业学报， 2012， 23(1)： 39-44.

Han Jun, Xiang Yu, Lu Jing. Analysis of Vibro-acoustic characteristics of a cavity with passive constrained layer damping[J]. Journal of Guangxi University of Technology, 2012,23(1)： 39-44. (in Chinese)

[8] 屈维德. 机械振动手册[M]. 北京： 机械工业出版社， 1992.

[9] 殷祥超. 振动理论与测试技术[M]. 徐州： 中国矿业大学出版社， 2007.

[10] 常冠军. 粘弹性阻尼材料[M]. 北京： 国防工业出版社， 2012.