单轴面内压缩功能梯度材料矩形板的弹塑性屈曲和后屈曲

陈飞超， 黄怀纬

(华南理工大学 土木与交通学院， 广东 广州 510640)

0 引 言

功能梯度材料定义为由多匀质材料层组成的复合叠层， 各匀质材料层属性按照TTO均匀化模型给定. 陶瓷/金属功能梯度材料(Functionally Graded Materials， FGM)产生于1986年[1]， 是一种新型耐热材料. FGM中陶瓷和金属的共混比率沿材料厚度方向从0到1呈现连续的变化， 使材料宏观性能连续过渡， 避免了传统叠层复合材料由于界面物性不连续而导致的应力集中现象发生. 特别是在极度恶劣的热环境下， FGM具有优异的抗裂和耐热性能. 目前， FGM的应用领域正逐步被拓展， 是一种极具应用前景的新型工程材料[2].

近年来， 各国学者对FGM板壳结构的力学性能进行了广泛而深入的探索， 特别是对于弹性屈曲问题的研究， 已取得许多卓有成效的成果. Feldman等[3]通过经典板理论， 研究了面内荷载下弹性FGM矩形板的线性屈曲问题； Javaheri等[4]通过变分法研究了FGM矩形板在面内荷载下的屈曲行为； Yang等[5]基于高阶剪切变形板理论， 对FGM矩形板的动力稳定性进行了分析； Morimoto[6]等通过Galerkin法研究了FGM矩形板在局部加热情况下的热屈曲问题； Asseaee等[7]对FGM矩形板横纵比对屈曲性能和后屈曲刚度的影响进行了分析； Sherafa等[8]通过最小势能法， 分析了几种不同几何特性的FGM矩形板单轴压缩屈曲临界荷载的变化； 陈江[9]采用线性理论， 用数值计算方法分析了FGM板的前屈曲力学行为； 张永强[10]采用半解析方法计算FGM圆柱壳的弹塑性临界荷载； 邵玉龙[11]等将二阶一致无网格法应用于FGM板， 结果表明这种计算方法大幅度提高了FGM结构的计算效率.

尽管FGM板壳结构弹性屈曲理论已较为完善， 但对于FGM板壳弹塑性屈曲和后屈曲问题的研究仍十分有限. 为探索材料物理非线性效应对FGM板结构屈曲及后屈曲性能的影响， 本文采用有限元程序ABAQUS对FGM矩形板的弹塑性屈曲和后屈曲问题进行了数值模拟， 分析中计入了材料物理非线性和结构几何非线性的双重影响.

1 材料属性

通常情况下陶瓷组分在厚度方向的分布服从幂律分布[3]， 即

Vc=(0.5+z/h)k,Vc+Vm=1,(1)

式中：V表示组分体积含量， c和m分别对应于陶瓷相和金属相；k为组分参数；z为板内点到板中心面的距离， 偏向陶瓷面取正；h为板厚度.

为了准确模拟FGM沿厚度方向渐变的材料属性， 借鉴复合材料分层模型的定义方法， 将FGM沿厚度方向划分足够多的匀质层， 各匀质层的材料属性由共混材料均匀化的TTO模型[9,10]决定. 陶瓷属于脆性材料， 假设在变形过程中陶瓷组分材料始终保持弹性， 那么FGM的杨氏模量E(z)、 泊松比v(z)、 屈服强度σy(z)、 唐氏模量Et(z)分别表示为

(2)

式中：l1=(q+Ec)/(q+Em);l2=(q+Ec)/(q+Etm);q为应力-应变传递数， 且q≥0. 当q=0时有σy=σym， 即一旦金属材料屈服， 则FGM材料也将屈服. 以下计算中， 根据文献[11]采用TiB/Ti FGM的材料参数， 选取q=4.5 GPa， 其陶瓷和金属组分材料的弹塑性材料属性为

Ec=375 GPa,vc=0.14,

Em=107 GPa,vm=0.34,

Etm=14 GPa,σym=450 MPa.

2 计算方法

采用有限元程序ABAQUS对FGM矩形板的弹塑性屈曲问题进行数值模拟， 由于计入材料的物理非线性和结构变形的几何非线性效应， 故本征值屈曲分析方法无法适用， 因此调用Riks算法开展计算工作.

FGM矩形板长为a， 宽为b， 厚度为h， 板两边固支， 另两边自由， 如图1(a)所示. 为使板结构具有屈曲构型， 必须引入初始缺陷， 本文以偏心位移加载. 单轴面内压缩时， 首先将B支座水平平移微小初始偏心位移Δ′， 再对C滑块施加铅垂位移Δ， 如图1(c)所示， 计算过程中以铅垂方向的反力作为实际的面内单轴压缩力.

图 1 FGM矩形板的几何尺寸、 边界条件及轴向加载方式Fig.1 Geometry size, boundary conditions and axial loading mode of FGM rectangular plates

定义FGM板材料属性时， 将材料沿厚度方向分为20个匀质叠层， 取各层中面位置的材料属性， 结合式(1)和(2)定义该匀质层的材料属性. 表 1 为k=1的情况下部分叠层中面的材料属性. 根据模型试算结果， 当叠层数大于20时， 计算结果趋于稳定， 因此认为将FGM板划分20个匀质层能够满足计算精度的要求.

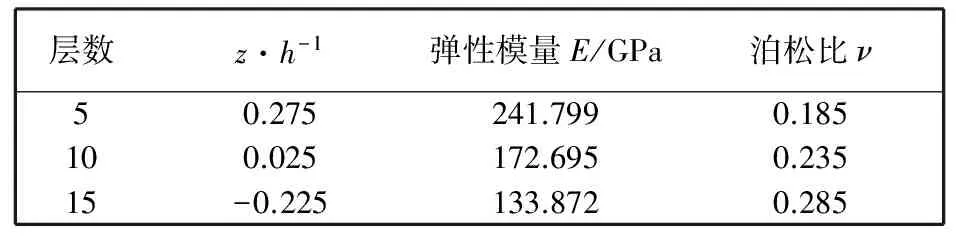
表 1 部分匀质层的弹性性能

FGM板的模型通过三维壳单元S4R来进行定义. 为保证网格尺寸的选择可满足计算精度的要求， 同时初始偏心位移对数据精度不产生影响， 需要在前续处理时分析网格尺寸和初始偏心位移对屈曲临界荷载的影响. 组分参数k分别取0.1,1，10的情况下， 取网格尺寸为1～3 mm， 初始偏心位移D′在0.01～5 mm 范围内变化， 图 2 给出了网格尺寸和初始偏心位移对屈曲临界荷载的影响. 结果表明网格尺寸和初始偏心位移在上述范围内变化时， 屈曲临界荷载几乎不变. 因此认为， 当网格尺寸小于3.0 mm时， 计算具有足够的精度； 同时， 当D′=5 mm时， 屈曲临界荷载对初始偏心位移的变化不敏感. 以下计算取用的网格尺寸为2.0 mm， 为模拟完善FGM板， 初始偏心位移取较小值 0.01 mm.

图 2 网格尺寸和初始偏心位移对屈曲临界荷载的影响Fig.2 Effects of mesh size and initial eccentric displacement on the buckling critical load

为验证本文算法的准确性， 选取相应的计算参数采用Riks算法进行数值模拟， 文献[12]得到了四边简支匀质弹性矩形板的后屈曲平衡路径的理论解， 如图 3 所示， 可见两者是一致的. 注意到， 计算结果显示匀质弹性矩形板具有稳定的后屈曲平衡路径， 这与实际是相符的.[13]

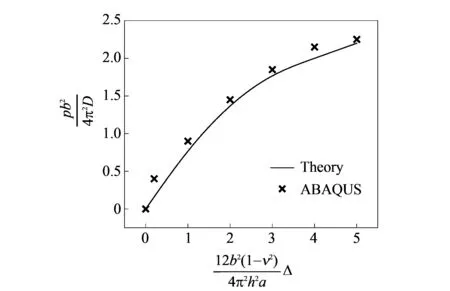
图 3 计算结果的验证Fig.3 Verification of the calculating results

3 结果分析

根据屈曲时材料所处的弹塑性状态， 结构屈曲可分为弹性屈曲、 弹塑性屈曲和塑性屈曲3种. 一般来说， 厚度较小时， 板发生弹性屈曲， 随着厚度的增大， 将发生弹塑性屈曲， 甚至塑性屈曲. 为分析FGM矩形板的弹塑性屈曲问题， 必须首先确定适当的板厚范围.

考虑图 1 的边界条件， 取k=0.1,a=80 mm,b=40 mm， 板厚h在0.4～4.0 mm的范围内变化. 图 4 给出不同厚度FGM矩形板的屈曲临界荷载及屈曲时塑性应变能. 由图4(a)可知， 屈曲临界荷载均随厚度的增大急剧增大； 由图4(b) 可知， 当厚度h<1.5 mm时， 塑性应变能很小， 而当h>1.5 mm时， 塑性应变能急剧增大， 说明当板厚达到1.5 mm时， FGM板将开始发生弹塑性屈曲， 故h=1.5 mm为弹性屈曲与弹塑性屈曲的分界线.

图 4 屈曲临界荷载及屈曲时塑性应变能随板厚的变化Fig.4 The variation of the buckling critical load and plastic strain energy at the buckling point with the plate thickness

在板厚h分别为0.4,2.0,4.0 mm情况下， 结构屈曲时陶瓷表面和金属表面的等效塑性应变如图 5 所示.

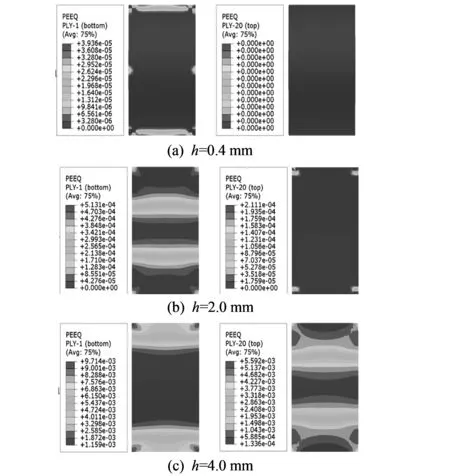
图 5 屈曲时陶瓷表面(左)和金属表面(右)的塑性应变Fig.5 Plastic strain of ceramic surface (left) and metallic surface (right) at buckling point

当h=0.4 mm时， 金属表面无塑性应变， 陶瓷表面产生了局部塑性应变， 但鉴于这一局部塑性应变十分微小， 故认为板仍处于弹性屈曲状态， 而局部的塑性应变是由固支边界产生的； 当h=2.0 mm时， 陶瓷表面的塑性应变较大， 而金属表面仍无塑性应变， 同时结合图4(b)， 说明板屈曲时材料已部分进入塑性状态， 故FGM板发生弹塑性屈曲； 当厚度继续增大到4.0 mm时， 金属表面和陶瓷表面整体均出现塑性应变， 说明此时FGM板发生了塑性屈曲， 因此塑性屈曲范围为h≥4.0 mm.

综上所述， FGM板的弹性屈曲范围为0

组分参数k是控制FGM组分材料沿厚度方向分布律的关键参数， 对FGM矩形板的屈曲临界荷载具有一定影响. 给定厚度h=2.0 mm， 组分参数k=0.1～5.0， 计算得到的屈曲临界荷载和轴向压缩位移， 如表 2 所示. 可知随着组分参数的增大， 屈曲临界荷载逐渐减小， 而屈曲时的轴向压缩位移增大. 由于FGM中， 陶瓷组分往往具有较金属组分高的弹性模量， 且其在变形过程中被假定为弹性材料， 而金属组分则被假定为弹塑性材料， 即FGM的塑性特征本质上源于金属组分材料的弹塑性属性， 因此， 当金属含量增大的情况下， 屈曲临界荷载将明显减小， 而屈曲时的轴向压缩位移相应有所增大.

表 2 不同组分参数下屈曲临界状态的结果

为了比较弹性和弹塑性FGM矩形板在屈曲及后屈曲性能上的差异， 本文取组分参数k分别为0.1， 1， 10进行了数值模拟. 分析时， 取厚度h=2.0 mm. 对于弹性FGM矩形板， 考虑两种组分材料均为弹性材料. 图 6 为弹性FGM矩形板和弹塑性FGM矩形板的轴向荷载-位移之间的关系曲线， 即基本平衡路径. 可知随着组分参数的增大， 无论是弹性FGM板还是弹塑性FGM板， 基本平衡路径均大大降低. 在组分参数相同的情况下， 弹性和弹塑性FGM板的前屈曲平衡路径是一致的， 弹塑性FGM板的屈曲临界荷载较弹性FGM板小. 同时弹性FGM板和弹塑性FGM板的后屈曲平衡路径存在较大差异， 弹性FGM板的荷载随着轴向位移缓慢增加， 呈现出稳定的后屈曲平衡路径， 而弹塑性FGM板的荷载却随着轴向位移的增加而减小然后趋于平稳， 呈现出不稳定的后屈曲平衡路径.

图 6 弹性FGM和弹塑性FGM矩形板的基本平衡路径Fig.6 Basic equilibrium paths of elastic and elastic-plastic FGM rectangular plates

4 结 论

本文采用有限元程序ABAQUS对面内单向压缩荷载下FGM矩形板的屈曲、 后屈曲问题进行了数值模拟， 考虑了初始偏心位移、 板体厚度、 材料组分参数、 材料塑性的影响， 得到了以下主要结论：

1) 初始偏心位移在0.01～5 mm范围内变化时对FGM矩形板的弹塑性屈曲临界荷载影响不大. 只要取一定的初始偏心位移， 即可模拟完善(无几何缺陷)FGM板的屈曲性能；

2) 随着FGM板厚的增大， 结构将发生弹塑性屈曲， 甚至是塑性屈曲. 对于单向面内压缩FGM矩形板， 板厚小于1.5 mm时将发生弹性屈曲； 板厚介于1.5～4.0 mm之间将发生弹塑性屈曲， 板厚大于4.0 mm将发生塑性屈曲；

3) 对于弹塑性屈曲问题， 组分参数的变化对FGM矩形板的屈曲、 后屈曲性能影响较大. 一般而言， 组分参数越大， 其陶瓷含量越低， 金属含量越高， 屈曲临界荷载随着组分参数或金属含量的增加而逐渐下降， 同时后屈曲平衡路径也随着组分参数的增加而降低；

4) 比较弹性和弹塑性FGM矩形板的屈曲、 后屈曲性能， 表明两者前屈曲平衡路径是一致的. 由于考虑了FGM的材料物理非线性效应， 后者相对于前者的屈曲临界荷载有所降低， 同时两者后屈曲平衡路径差异较大， 前者具有稳定的后屈曲平衡路径， 而后者具有不稳定的后屈曲平衡路径.

[1] Koizumi M. The concept of FGM[J]. Ceram Trans, 1993, 34(1): 3-10.

[2] 李云凯, 王勇, 钟家湘. 功能梯度材料[J]. 材料导报， 2012, 16(10): 9-11.

Li Yunkai, Wang Yong, Zhong Jiaxiang. Functionally graded materials[J]. Materials Review， 2012， 16(10)： 9-11. (in Chinese)

[3] Feldman E, Aboudi J. Buckling analysis of functionally graded plates subjected to uniaxial loading[J]. Compos Struct, 1997, 38(1-4): 29-36.

[4] Javaheri R, Eslami M R. Buckling of functionally graded plates under in-plane compressive loading[J]. Zeitschrift Fur Angewandte Mathematik Und Mechanik, 2002, 82(4): 277-283.

[5] Yang J, Liew K M, Kitipornchai S. Dynamic stability of laminated FGM plates based on higher-order shear deformation theory[J]. Computational Mechanics, 2004, 33(4): 305-315.

[6] Morimoto T, Tanigawa Y, Kawamura R. Thermal buckling of functionally graded rectangular plates subjected to partial heating[J]. International Journal of Mechanical Sciences, 2006, 48(9): 926-937.

[7] Assaee H, Hajikazemi M, Ovesy H R. The effect of anisotropy on post-buckling behavior of laminated plates using semi-energy finite strip method[J]. Composite Structures, 2012, 94(5): 1880-1885.

[8] Sherafat M H, Ovesy H R, Ghannadpour S A M. Buckling analysis of functionally graded plates under mechanical loading using higher order functionally graded strip[J]. International Journal of Structural Stability and Dynamics, 2013, 13(6): 1350033.

[9] 陈江. 功能梯度板屈曲有限元分析[D]. 扬州： 扬州大学, 2015.

[10] 张永强. 陶瓷/金属功能梯度结构弹性及弹塑性稳定性分析[D]. 广州： 华南理工大学, 2016.

[11] 邵玉龙, 段庆林, 李锡夔, 等. 功能梯度材料的二阶一致无网格法[J]. 工程力学, 2017, 34(3): 15-21.

Shao Yulong, Duan Qinglin, Li Xikui et al. Quadratically consistent meshfree method for functionally graded materials[J]. Engineering Mechanics, 2017, 34(3): 15-21. (in Chinese)

[12] Tohgo K, Masunari A,Yoshida M. Two-phase composite model taking into account the matricity of microstructure and its application to functionally graded materials[J]. Compos Part A, 2006, 37(3): 1688-1695.

[13] Bocciarelli M, Bolzon G, Maier G. A constitutive model of metal-ceramic functionally graded material behavior: Formulation and parameter identification[J]. Computational Materials Science, 2008, 43(1): 16-26.

[14] Jin Z H, Paulino G H, Jr R. Cohesive fracture modeling of elastic-plastic crack growth in functionally graded materials[J]. Engineering Fracture Mechanics, 2003, 70(14): 1885-1912.

[15] 沈惠申, 张建武. 单向压缩简支矩形板后屈曲摄动分析[J]. 应用数学和力学， 1998， 9(8): 741-752.

Shen Huishen, Zhang Jianwu . Perturbation analyses for the postbuckling of simply supported rectangular plates under uniaxial compression[J]. Applied Mathematics and Mechanics， 1998, 9(8): 741-752.

[16] 韩强. 弹塑性系统的动力屈曲和分叉[M]. 北京: 科学出版社, 2000.