精挑细选 精雕细琢
曹艳

摘 要: 例题的选择与设计的成功与否直接关系复习课的成败,只有好的例题才能撑起一堂好的复习课。因此,复习课例题要做到精挑细选,精雕细琢,让我们复习课效率更高。
关键词: 精挑;细琢;中考
例题教学是数学教学的主要组成部分,通过例题教学可以帮助学生复习巩固以前所学知识,是使学生的数学知识转化为数学能力的重要环节。
在初三复习教学中,许多教学的重点难点以及学生没有完全掌握的知识点、易错点等都需要复习课来强调、落实、理解和纠正,题型和解法的熟练也需要通过复习课来实现。所有这些的落脚点,都是复习课中的例题。因此,例题的选择与设计的成功与否直接关系复习课的成败。只有好的例题才能撑起一堂好的复习课。下面以一次公开课为例谈谈中考复习课例题的选择。本着复习课例题灵活性强,知识覆盖面大,难易适中的原则,从众多的符合本课时内容的题目中最终挑选并改编了两道例题。
一、 充分利用课本例习题进行拓展变式
纵观我市历年的中考题,发现无论是小题还是综合题有很多都能在课本上找到原形。课本习题例题都是经过专家精心筛选具有一定的典型性和代表性,其中有许多习题蕴含着丰富的内涵和背景,他们是编拟中考题的源泉。所以,选择复习课例题是优先考虑课本中的例题与习题,进行适当演变、拓深,使其源于教材,又不拘泥于教材。
例1 由苏科版八年级下册的课本P87页例题改变而来,例2来源于八下课本94页17题,在原题的基础上进行了改变拓展。
例题1借助中点四边形,将本节课所复习的四种特殊四边形的判定集中在一个学生熟悉的图中。
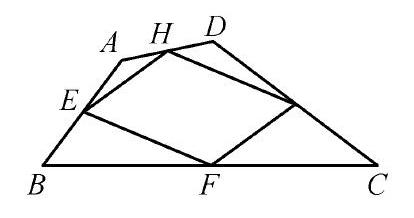
原题:如图,在四边形ABCD中,AC=BD,点E、F、G、H分别是边AB、BC、CD、DA的中点。
求证:四边形EFGH为菱形
改编后:例1 如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点。
(1)要使四边形EFGH为菱形,四边形ABCD需要满足什么条件?请说明理由;
(2)当 时,四边形EFGH为矩形;
(3)当 时,四边形EFGH为正方形。
例题1结束后,根据学生的实际情况,我們将该例题进行变式:
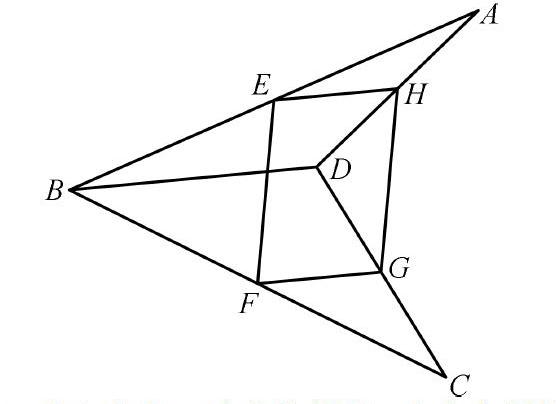
变式1 改变中点在四边形中的位置。将其中两点F、H变成对角线的中点,则四点还能构成平行四边形吗?类似的,若是矩形或菱形或正方形,又要添加什么条件?
变式2 改变四边形形状,将凸四边形变成凹四边形,例题一的结论还成立吗?
变式3 改变中点。试着将例题1中点全部换成三等分点,图中出现的还是平行四边形吗?如果是n等分点呢?
这样,题目就不拘泥于中点四边形了,一题多变,一道数学题通过联想、类比、推广,可以得到一系列新的结论,甚至得到更一般的结论,积极开展多种变式题的求解,有助于学生应变能力的养成,培养学生发散思维的形成,增强学生面对新问题敢于联想分析予以解决的意识。
二、 复习课中的例题应有别于新课,既要立足双基,也要覆盖面广
初三的复习时间紧促,不允许我们像讲新课一样开展复习教学,这就对复习课提出了更高的要求:既要让学生在课堂上熟练掌握获得基本解题方法,又要保证复习的进度。所以复习课的例题涉及内容不能单一,例题所覆盖的面要广。在复习过程中不仅应该重视基础,把握教材的重点内容,还要注意知识的不断深化,特别要注意数学知识之间的关系和联系,逐步形成和扩充知识结构系统,在大脑记忆系统中构建“数学认知结构”,形成一个条理化、有序化、网络化的有机系统。例如四边形的例题中可以渗透三角函数、相似全等三角形、函数求最值等,让学生感受代数和几何是相辅相成,浑然一体,密不可分的。在第一轮复习中,我们始终要狠抓基础,数学基础是理解、掌握数学知识的关键,是灵活运用所学公式性质定理、增强解题能力的基础。基础知识和基本技能也是复习的根本所在。因此,我们在复习课上例题的选择应该立足双基,充分考虑例题所承载的基础知识和基本技能,有助于帮助学生回顾与复习数学基础知识,引导学生在应用数学知识的基础上强化基本技能。所以选择例题应避开过烦、过偏、过难的题目。同时例题还要包含多个知识点,或能够全面的反映考纲要求,通过例题讲解能够达到综合运用知识和解决问题的能力,同时也能够建构知识体系。经过多次筛选,最终确定的这两个例题,题目看起来并不陌生,学生稍微动动脑筋就能做出来,但看似简单的题目,所蕴含的知识点却不少。比如例题一,集中考查平行四边形、矩形、菱形、正方形的判定定理的应用,同时也复习了中位线定理。这些都是考纲要求学生必须掌握的基础知识,在充分理解中位线定理和特殊平行四边形判定的基础上,学生能够形成熟练运用知识解决问题的基本技能。例题二在例题一的基础上提高一个小层次,没有直接给出直角以及对角线平分的条件,而是让学生先去寻找发现,考查的知识点除了特殊平行四边形的判定外,还有平行线性质、角平分线定义及平角等相关知识。
三、 所选例题要灵活,要具有开放性
以例题2为例:(原题)如图,△ABC中,点O是AC边上任意一点(不与AC重合),过O平行于BC的l分别交∠ACB的平分线于点E,交∠ACB的外角∠ACD平分线于点F。
(1)OE与OF相等吗?证明你的结论
(2)确定O点位置使四边形AECF为矩形,并证明你的结论
(改编后):△ABC中,点P是AC边上一个动点,过P作直线EF∥BC,交∠ACB的平分线于点E,交∠ACB的外角∠ACD平分线于点F。
经过试讲发现直接给学生要证明的结论会限制学生的思维,而且一部分学生会埋头做题,不去理会题目所蕴藏的知识点和方法。我们尝试直接去掉问题,最后连图形也去掉,让学生在读题画图的过程中发现更多的结论。这类问题结论开放,学生可以自由探索,自由发展,这样也可以让所有不同层次的学生体验到不同的成就感。直接给结论,有部分成绩不太好的孩子可能没有一点思路,但是不给结论,这部孩子至少能根据两条角平分线得到直角,根据平行线能得到内错角或同位角相等,再进一步,结合这两条结论,可以得到等腰三角形。在得到两个等腰三角形之后,学生们可以结合今天所复习内容,联想到能否出现特殊四边形,要得到矩形比较容易,此时可以追问能否得到正方形,如果不可以,原来的三角形可以添加什么有条件,这样就成了条件和结论都开放的问题了。这道开放题留给学生较大的想象空间,在探索过程中,充分显示出思维的多样性,同时也体现了不同学生数学学习的个性化。在教学中引导学生多角度、多层次、多渠道地解答开放性问题,培养学生的个性,从而全方位培养学生的创造能力。
四、 复习课的例题设计要有梯度
现在中考题知识面广,起点低,坡度缓,难度适中,区分度好,基本做到稳中有变、稳中有活、稳中有新,数学特点比较特出。试题由易到难结构
3∶4∶2∶1,以体现“夯实基础,注重能力,严格标准,有所创新”为原则,也就是说有70%的题目绝大多数的学生都能做。同样,在复习课中我们也应该控制好例题的难度,设计好梯度,要使绝大多数的学生通过“跳一跳能够着”,否则会影响学生的做题积极性。其次,我们通过开放结论,将题目的任务一步一步呈现,学生得到简单结论后,通过不断追问,一步一步再缩短与目标的距离,从而让绝大多数学生都能够心情愉悦的体验成功。

