异步电机矢量控制温度补偿技术研究
梅建伟,田艳芳,罗 敏,刘 杰,魏海波
(湖北汽车工业学院 电气与信息工程学院,湖北 十堰 442002)
0 引 言
转子磁场定向矢量控制系统在异步电机变频调速中应用广泛,但是磁链、转矩指令等参数的计算严重依赖于转子时间常数,只有获得较为准确的转子时间常数才能实现定子电流励磁分量和转矩分量的解耦控制[1],而电机转子温升和磁通又影响转子时间常数,随着电机运行工况的变化,转子时间常数会发生显著的变化,实验证明,在不计弱磁和磁饱和现象的情况下,仅仅由电机的温升而引起的转子电阻的变化就达到转子电阻标称值的0.75~1.5倍。转子时间常数的剧烈变化,造成电机的磁场定向出现偏差,电机出现弱磁或者过励磁运行状态,输出扭矩波动,线电压升高,电机效率降低,电流发生畸变[2],从而造成电机发热,而电机过热又会加剧转子时间常数的偏差,进入恶性循环,因此准确的获得转子时间常数是良好的矢量控制的前提[3- 4]。笔者着重讨论在温度变化造成转子时间常数变化时,针对转子时间常数对异步电机稳态性能的影响,提出了一种异步电机矢量控制系统温度补偿方法,即以定子绕组温度为参考,在电机不同工况运行时,建立定转子温度变化关系模型,从而得到异步定转子绕组电阻变化模型,利用该变化的阻值来改变转子时间常数补偿量,以此修正控制系统设定的转子时间常数,在理论推导的基础上,结合MATLAB进行了仿真。仿真结果验证了理论分析,对异步电机矢量控制性能优化具有一定的借鉴意义。
1 温度变化对电机控制系统性能影响
在旋转坐标系下定子和转子电压方程:
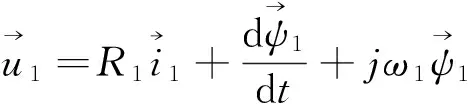

(1)
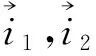
将折算后的转子磁链方程代入旋转坐标系下转子电压方程,得到:
(2)
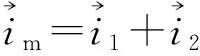
同步坐标系下转子电压方程为
(3)
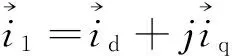
结合同步坐标系下转子电压方程可得:
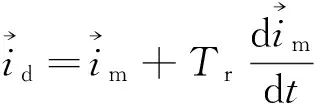
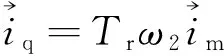
(4)

(5)
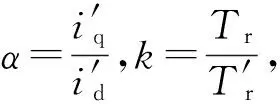
1.1 对励磁电流分量的影响
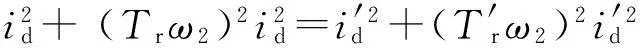
(6)
时间常数发生变化时,我们只考虑温度和集肤效应对转子电阻的影响,因此系数k的数值应该在(0,2)的范围内。
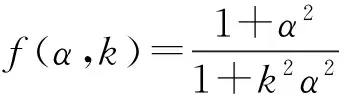
当将k作为常数,载荷变化时,此时讨论励磁电流分量随载荷变化的关系。
(7)

当α∈[α1,α2] 时:
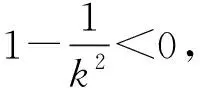
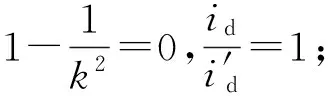
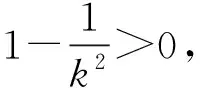
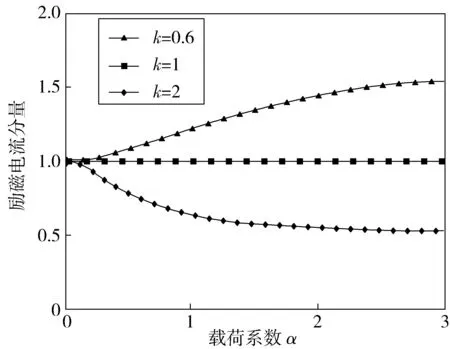
图1 励磁电流分量与载荷系数关系Fig. 1 Relation between excitation current component and load coefficient
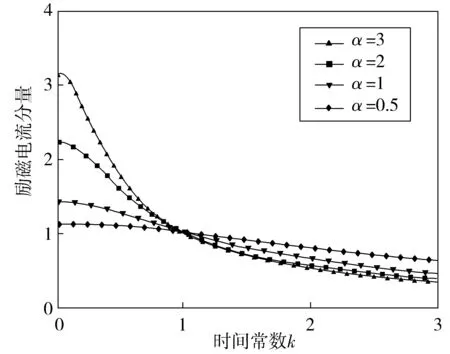
图2 励磁电流分量与时间常数关系Fig. 2 Relation between excitation current component and rotor time constant
1.2 对转矩电流分量的影响
(8)
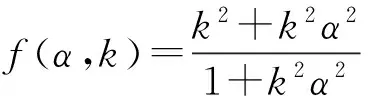
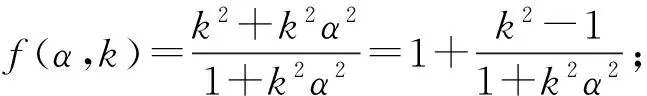

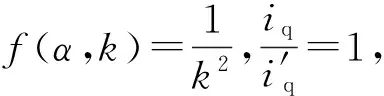
当α∈[α1,α2] 时:
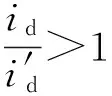
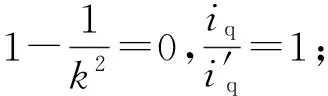
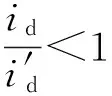
1.3 对转子磁链的影响
转子磁场定向时,稳态时磁链ψr=Lmid,故:

与励磁电流的变化规律相同。
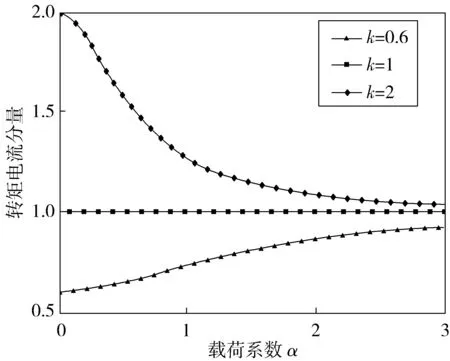
图3 转矩电流分量与载荷系数关系Fig. 3 Relation between torque current component and load coefficient

图4 转矩电流分量与时间常数关系Fig. 4 Relation between torque current component and rotor time constant
1.4 对电磁转矩的影响
转子磁链定向同步旋转坐标系中的电磁转矩为
(9)
(10)


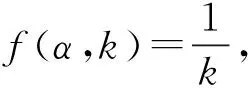
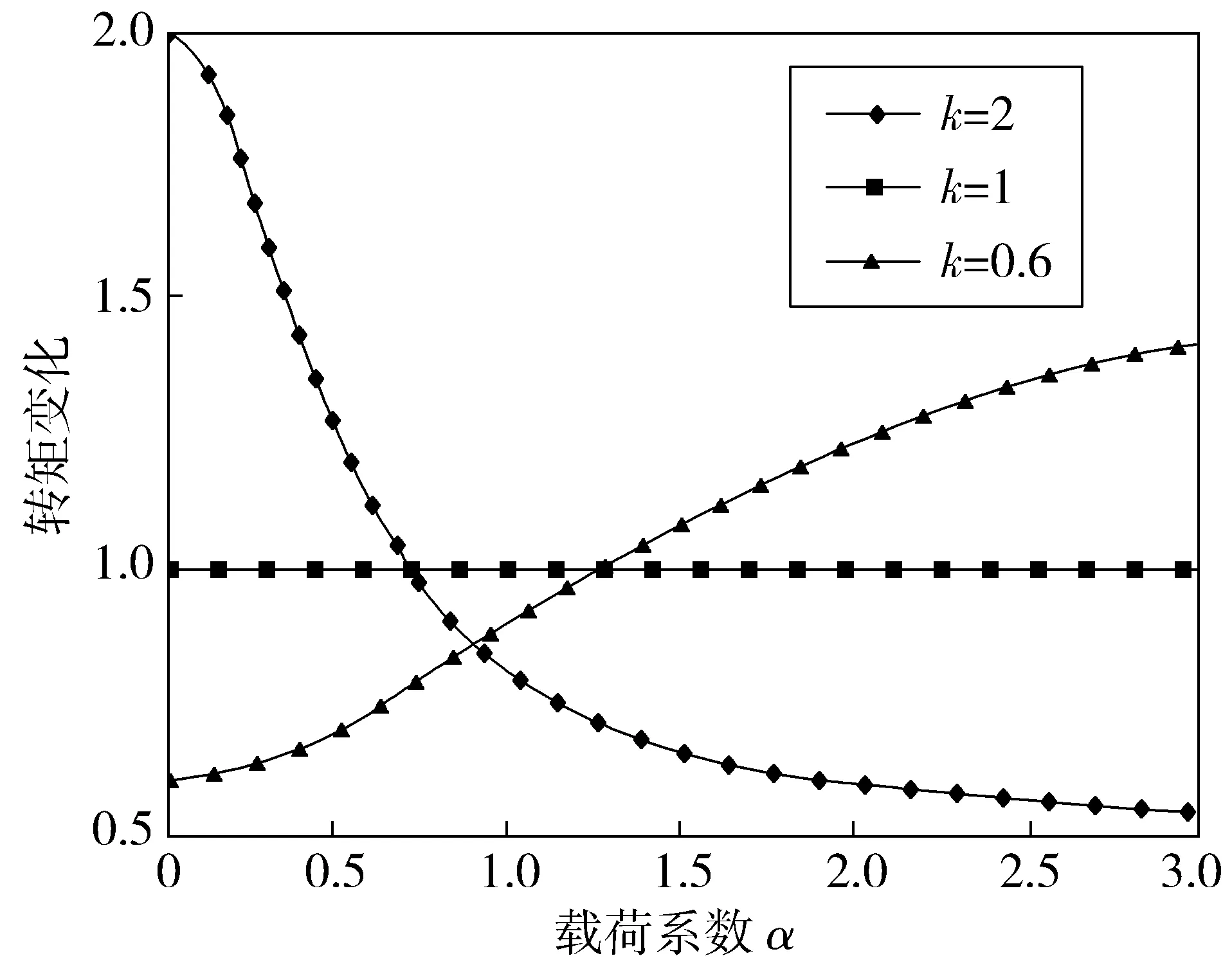
图5 转矩与载荷系数关系Fig. 5 Relation between torque and load coefficient
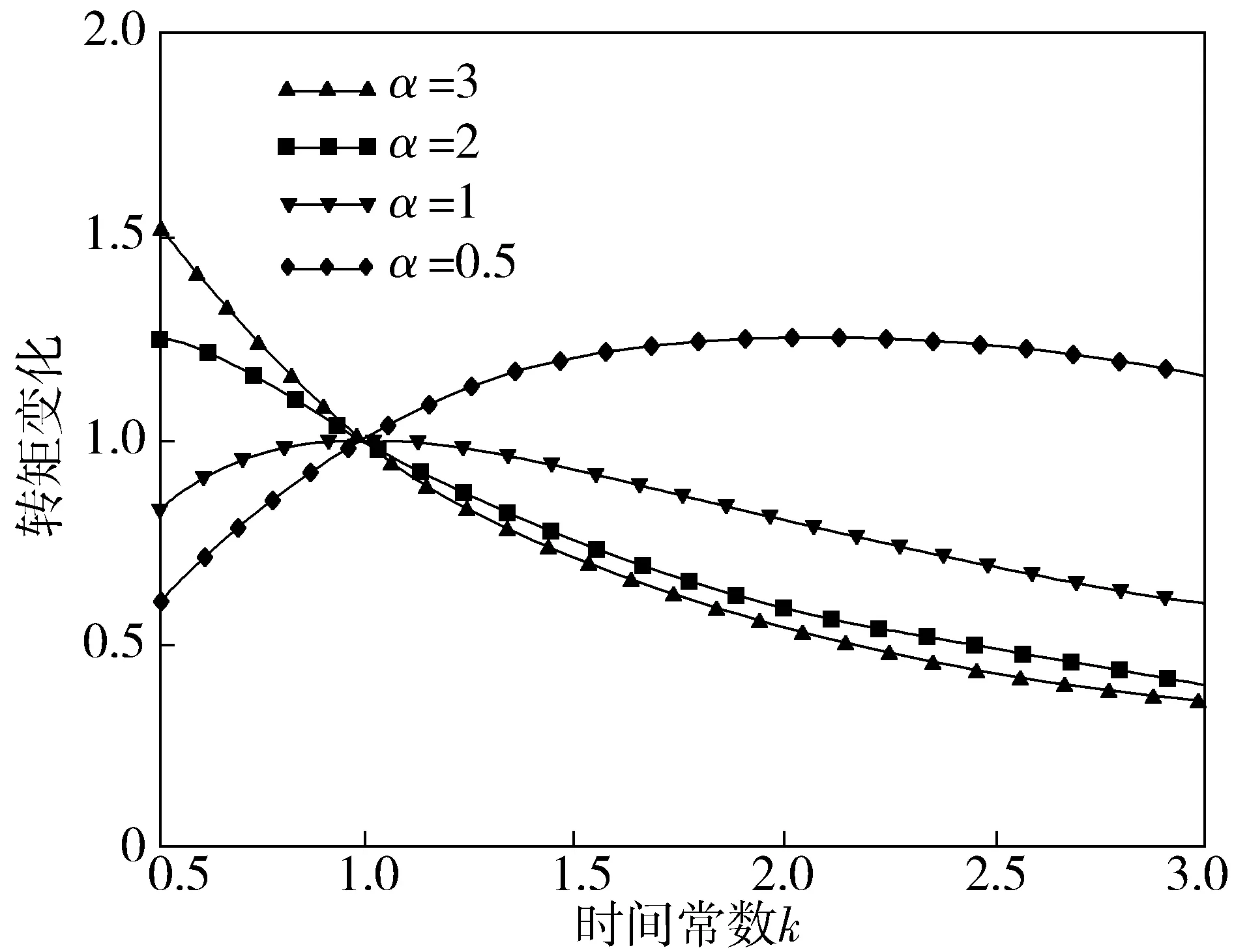
图6 转矩与时间常数关系Fig. 6 Relation between torque and rotor time constant
2 温度补偿技术
在异步电机矢量控制系统中,转子时间常数的变化影响矢量控制系统的稳态和动态特性,为了补偿转子温度变化而导致转子时间常数的变化,采用温度补偿电路测量电机温度,并转换为相应的转子时间常数,从而对转子时间常数的变化进行补偿,改善矢量控制系统的性能。
2.1 定子温度检测原理
采用的温度传感器的型号为:KTY84-150,测量温度的范围为:-40°~300°,温度变化时其电阻呈正温度系数变化,且随温度变化曲线如图7。
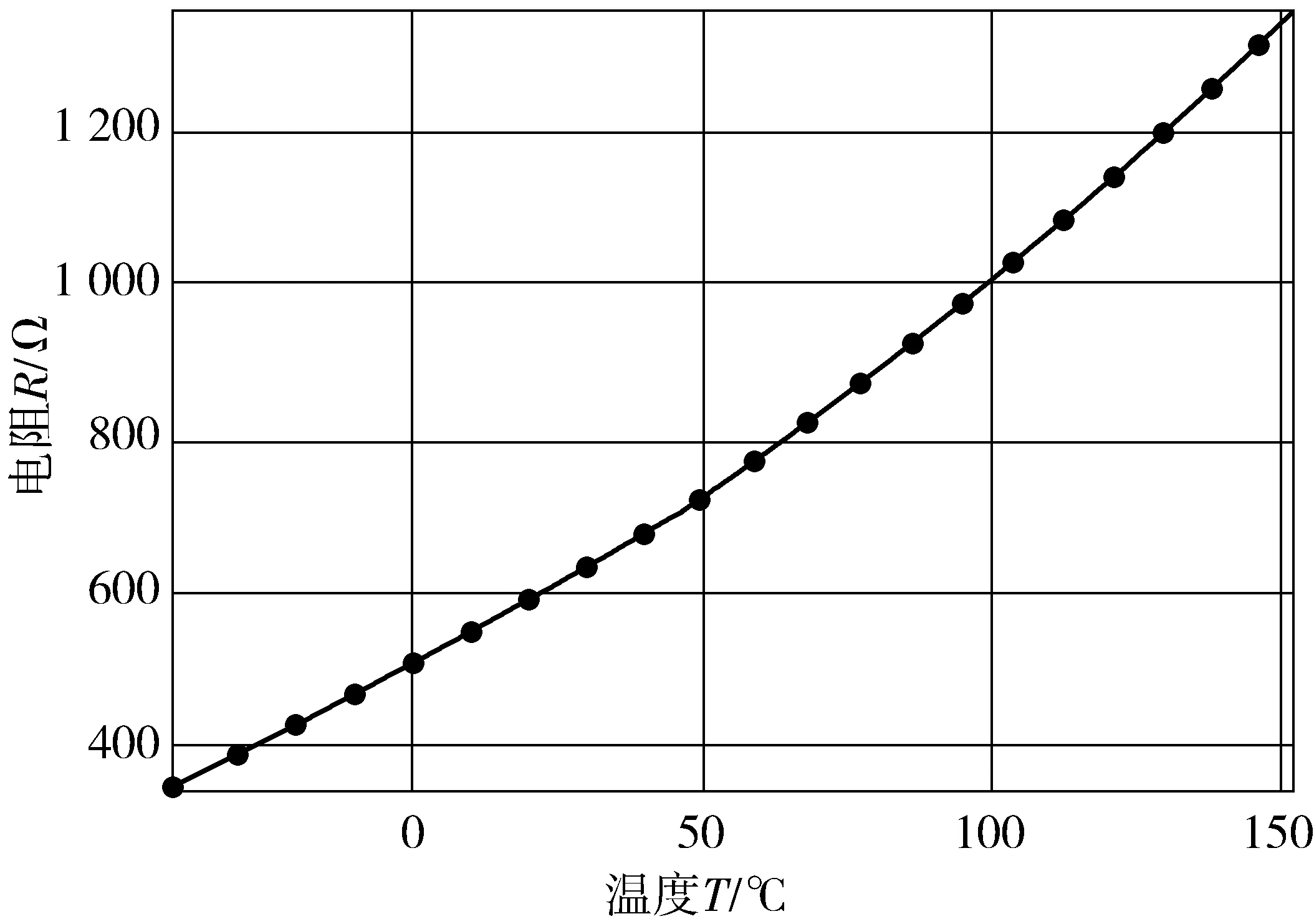
图7 电阻与温度关系Fig. 7 Relation between resistance and temperature
拟合得到的电阻随温度变化的数学关系式为
R=0.011 03t2+3.916t+498.1
温度补偿电路如图8,图8所示的电路将温度变化引起的电阻变化的信号转变为电压信号,经过预处理电路以后直接送入TMS320F2812的模拟量输入通道ADCINA3。

图8 温度补偿电路Fig. 8 Temperature compensation circuit
2.2 转子时间常数温度补偿原理
由于转子在机壳内部,其温度难以直接测量,利用红外测温仪测量轴温得到异步电机转子的温度,具体测试方法为:当电机在额定负载情况下运行时,在没有冷却水和风冷的情况下,采用自然冷却的方式,在不同的时刻点,同时得到异步电机定子绕组的温度和转子绕组的温度,根据测量的异步电机定转子温度数值,采用曲线拟合的方式,可以得到定转子温度的函数关系:
t转子=f1(t定子)
(11)
转子绕组大多采用铜线绕制,转子电阻会随着温度的变化而发生变化,转子电阻的变化引起转子时间常数的变化,假设转子时间常数与转子温度的变化关系为
Tr=f2(t转子)
(12)
由上述两式即可得到转子时间常数与定子温度之间的关系:
Tr=f2[f1(t定子)]
(13)
2.3 定转子温度函数偏差的影响
假设定转子温度的函数关系为
t转子=f1(t定子)+Δf1(t定子)
(14)
式中:Δf1(t定子)是定转子温度函数关系的偏差;
根据式(13),得到转子时间常数与定子温度之间的关系:
Tr=f2[f1(t定子)+Δf1(t定子)]=f2[f1(t定子)]+Δf2(t定子)
(15)
式中:Δf2(t定子)是定转子温度函数关系的偏差;当Δf2(t定子)>0时:引起理论计算的转子时间常数偏大,即控制系统用的转子时间常数比电机实际的转子时间常数大;当Δf2(t定子)<0时:引起理论计算的转子时间常数偏小,即控制系统用的转子时间常数比电机实际的转子时间常数小。
3 温度对控制系统影响仿真
3.1 仿真环境
建立矢量控制系统模型,温度变化时转子电阻会发生变化,转子时间常数也会跟随变化,仿真模型中假定在温度变化时电机参数不发生改变,改变矢量控制系统的转子时间常数。仿真模型采用定子电流励磁分量和转矩分量闭环控制的矢量控制系统,异步电机的定转子的相关参数为:RS=0.087 Ω,LS=0.8 mH,Rr=0.228 Ω,Lr=0.8 mH,Rr=0.228 Ω,Lr=0.8 mH,Lm=34.7 mH,J=1.662 (kg·m2),P=2,TL=40 (N·M),设定的转子目标转速为ωr=300转/分。
3.2 仿真波形
不同时间常数下定子励磁电流曲线、定子转矩电流曲线、电磁转矩曲线、转子磁链曲线以及转子转速曲线如图9。
3.3 结果分析
温度升高时,转子电阻增大,转子时间常数减小,电机真实的转子时间常数小于控制系统设定值;温度降低时,转子电阻减小,转子时间常数增大,电机真实的转子时间常数大于控制系统设定值。
由图(2)、图(4)、图(6)可知,转子时间常数变大时,励磁电流分量减小,转子磁链减小,可能出现欠励磁,转矩电流分量增大;转子时间变小时,励磁电流分量增大,转子磁链增加,可能出现过励磁,会导致电机饱和,电机发热,效率降低,同时转矩电流分量减小。
由图(1)、图(3)、图(5)可知,在不同的载荷系数下,转矩随转子时间常数变化而变化很大,且使得电磁转矩波动明显加剧;载荷系数越大,对励磁电流分量的影响越重,载荷越轻,对转矩电流分量的影响越重。
由图9(c)、图9(d)、图9(e)可知,转子时间常数越大,响应速度越慢。


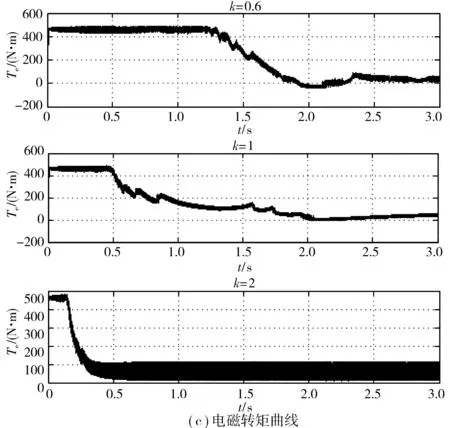
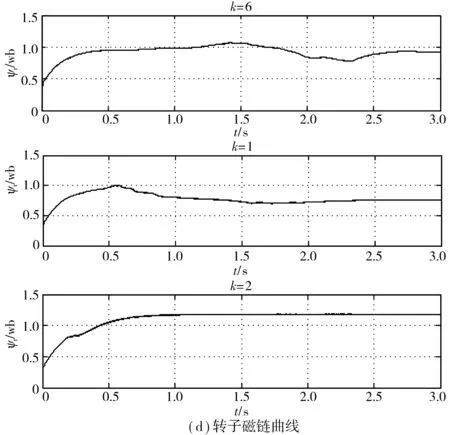
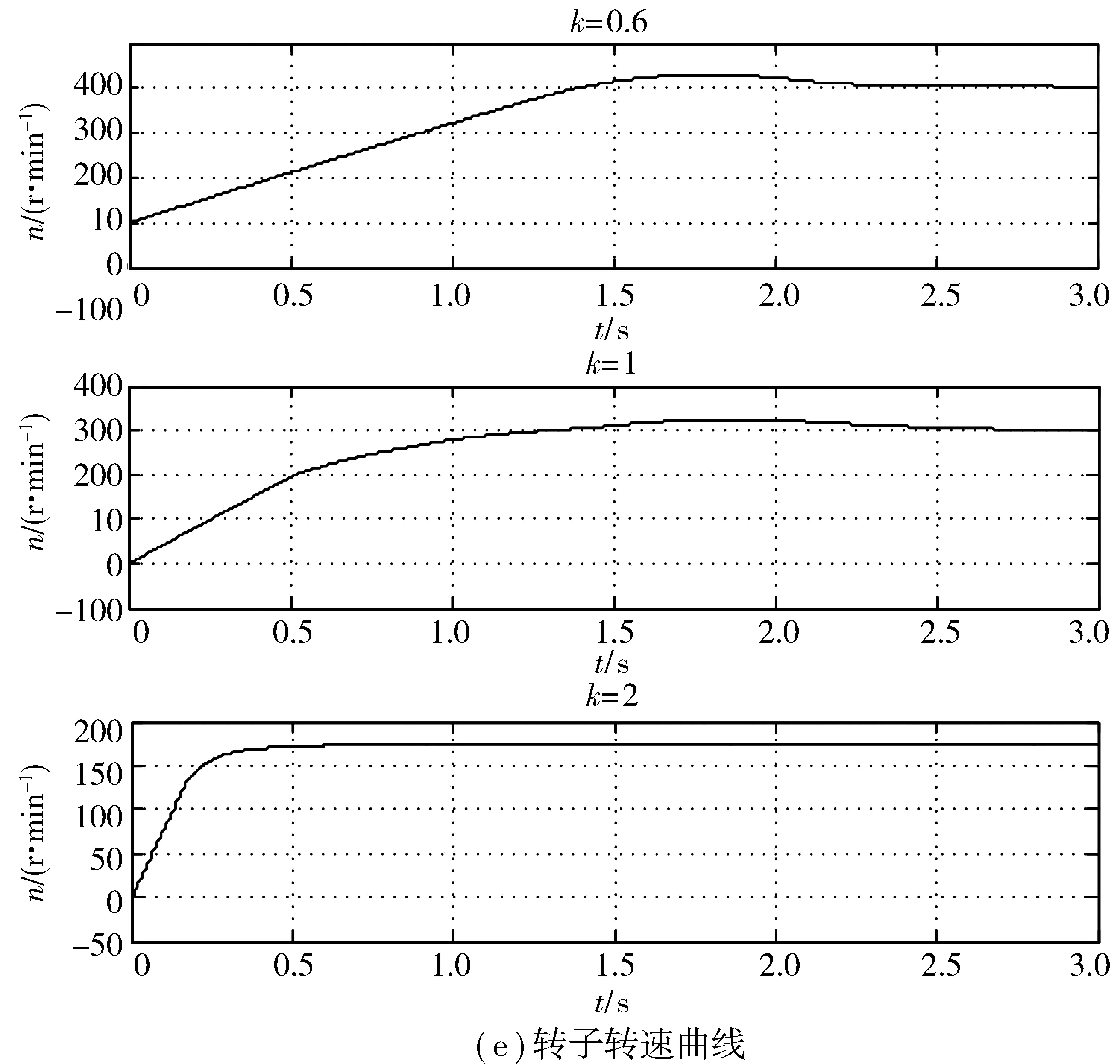
图9 转子时间常数影响Fig. 9 The influence of the rotor time constant
3.4 温度补偿技术对电机输出性能的影响
在仿真时发现,在经过对转子时间常数通过温度测量手段进行补偿后,相比补偿前,补偿手段有效的改善了系统的静态和动态性能,电机输出转矩波动量明显减小。同时电机励磁电流分量和转矩电流分量振荡现象基本消失。
当转子时间常数变化过大时,由于控制系统转子时间常数偏离了实际值,电磁转矩严重下降,PI控制器几乎失效,采用温度补偿技术后,从图9(e)上看该现象基本消失。
当转子时间常数处于较小值时,动态响应速度较慢,当进行温度补偿以后,从图9(e)可知,K=1时恢复正常。
4 结 语
结合转子磁场定向矢量控制系统,在不考虑转子电感变化时,由温度变化引起转子电阻和转子时间常数的变化,分析了转子时间常数不同值对定子电流的励磁电流分量、转矩电流分量、转子磁链、电磁转矩的影响,得出了一种根据定子绕组温度的变化补偿转子时间常数变化的模型,利用这些规律可以修正控制系统电机参数设定值,通过仿真验证了理论分析的正确性。该方法简单,便于工程应用,对工程实践具有一定的指导意义。
[1] 李汉强.基于磁通观测器的转差频率型异步电机矢量控制系统[J].自动化学报,1997,23(6):750-755.
LI Hanqiang. Slip frequency type vector control system for induction motor based on flux observer[J].ActaAutomaticaSinica,1997,23(6):750-755.
[2] 彭伟发,徐晓玲,邹娟.转差频率矢量控制仿真研究[J].华东交通大学学报,2009,26(1):67-70.
PENG Weifa,XU Xiaoling,ZOU Juan.Simulation of SF vector control[J].JournalofEastChinaJiao-tongUniversity,2009,26(1):67-70.
[3] BOSE B K.ModernPowerElectronicsandACDrives[M].Beijing:China Machine Press,2005.
[4] 崔霆锐,张立伟.矢量控制异步电机参数敏感性仿真研究[J].计算机仿真,2014,31(7):187-192.
CUI Tingrui,ZHANG Liwei.Parameter sensitivity simulation of vector controlled asynchronous motor drive system[J].ComputerSimulation,2014,31(7):187-192.
[5] 高建华.转子时间常数对异步电机矢量控制的影响[D].北京:中国科学院研究生院,2003.
GAO Jianhua.TheInfluenceofRotorTimeConstanttotheAsynchronousMotorVectorControl[D].Beijing:Graduate School of the Chinese Academy of Sciences,2003.

