多翼离心风机数值模拟中湍流模型的适用性研究

杨伟刚，蒋博彦，赵康发，王 军，李 斌

（1.华中科技大学，湖北武汉 430074；2.浙江省健康智慧厨房系统集成重点实验室，浙江宁波 315300）

1 前言

多翼离心风机叶片弯曲度大，叶道流道短、分离严重，蜗壳中也充斥着各种二次流动，其内部流场是一种复杂的三维非对称流动，这使得多翼离心风机的性能预测及内部流动研究十分困难。随着CFD技术的发展，应用数值计算的方式对风机内部流动进行模拟已成为风机气动性能设计和流场分析的重要手段。而三维湍流流场计算精度的高低，在很大程度上取决于所采用的湍流模型。文献［1］对κ-ε和SST κ-ω湍流模型在离心泵的模拟精度进行了分析，得出SST κ-ω对分离预测的准确度更高。文献［2］对4种湍流模型在双吸离心泵数值模拟中的适用性进行了分析，认为RNG κ-ε模型在计算精度和计算时间方面表现更好。侯祎华等采用Spalart-Allmaras （S-A）和Standard κ-ε模型对混流式转轮进行了模拟计算［3～5］，对比发现两者模拟结果相似，不同旋转机械中湍流模型具有不同的适用性和精度。然而在多翼离心风机的相关研究中，不同学者使用了不同湍流模型，文献［6～9］采用Standard κ-ε模型对多翼离心风机内湍流进行了计算，并验证了数值计算的准确性。文献［10］采用Realizable κ-ε对不同工况下的多翼离心风机进行三维数值模拟，研究了风机的典型几何参数对其性能的影响。文献［11］在多翼离心风机研究中分别用Standard κ-ε模型、RNG κ-ε模型和Realizable κ-ε模型进行了计算，发现3种κ-ε湍流模型结果接近，并且与试验结果比较吻合。文献［12］在多翼离心风机的叶片尾缘改型设计中采用SST κ-ω模型，并验证了数值模拟的准确性。但是，鲜有人对不同湍流模型在多翼离心风机数值模拟中的适用性和精度展开相关研究。

本文以气动性能和PIV的试验结果为参照，判断常用的3种湍流模型：单方程S-A模型，两方程Realizable κ-ε和SST κ-ω模型所得模拟结果的准确性，对比出最能准确模拟多翼离心风机气动性能和内部流动细节的湍流模型，为该型式风机外特性和内流场的准确数值模拟提供依据。

2 研究对象

试验风机为一低压双吸多翼离心风机，其几何模型如图1所示，主要由外部风道、蜗壳、叶轮、出风罩4部分组成。叶轮外径D2=254 mm，轮毂比υ=0.827，叶轮进口角β1=76°，出口角β2=159°，叶片数Z=60。气流由外部风道下方进入，分别从叶轮前后段进入风机。由于叶轮后段内部安装电机，进气状态受到影响，气体主要通过前进风口进入风机。

图1 试验风机模型

3 试验方法

3.1 PIV测试系统

本试验采用的PIV系统由激光器、同步器、CCD相机、数据采集处理等组成。采用癸二酸二辛酯（DEHS）为示踪粒子，粒径为1μm左右。激光照射和拍摄窗口处用有机玻璃替换原材料。在测量蜗壳内部流动时，每对图像的拍摄时间间隔Δt=100 ns，每秒钟拍摄15幅结果；在测量进口区域时Δt=300 ns，每秒钟拍摄5幅结果。每次测量选取连续100幅速度场结果做时间平均来表示测量平面的定常流动形态。

3.2 测量工况

试验台测试原理完全参照GB/T 17713-201，试验装置如图2所示。试验中，风机电机为交流电机，被测烟机出风口通过连接器与空气性能试验装置的十字整流器连接，烟机气流依次通过连接器、十字整流器和扩散段后进入减压筒。通过变换减压筒下游孔板的开孔直径，测得每一个工况点的动态测试数据，并通过计算得出空气性能试验结果。试验应有足够的持续时间，以获得一致的结果和达到预期的试验精度。每测一个流量点应有一定的时间间隔，并应同时测量流量、全压、静压、转速和轴功率。风机气动性能试验在变转速条件下进行，为了方便数值计算，现换算成同一转速n=1175 r/min，换算后整机的风机性能曲线如图3所示。

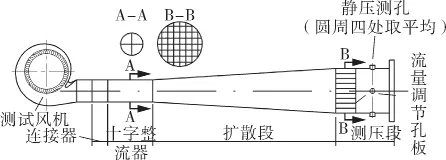
图2 性能试验台示意

图3 气动性能及试验工况

本次PIV试验选定最高效率点n=1175 r/min，QBEP=16.899 m3/min为测试工况点，如曲线标注G所示。

3.3 测量区域

PIV测量区域为风机进口及蜗壳内部流场。图4（a）展示了测量区域截面A，B的范围，测量风机进口流场时选取截面A，位置距蜗壳前面板40 mm；蜗壳处选取截面B，位置对于前段叶轮50%的叶高。图4（b）为测量区域沿轴向的位置。

图4 PIV拍摄位置及区域

4 数值模拟

4.1 网格划分

为便于数值计算，现将风机流域划分为5部分：外部方腔风道、叶轮、蜗壳、出风罩和出口延长段，风机计算模型如图5所示。

图5 计算模型

本文对整机用Star-CCM+软件进行多面体网格划分（图6）。由于叶片表面和蜗壳壁面易发生边界层分离，因此在这些位置布置棱柱边界层网格（图7），并对边界层网格做出适当调整以确保壁面与第一层网格节点之间距离满足不同湍流模型的要求。为确保计算精度，交界面上的网格尺寸大小保持一致，叶轮区域和蜗舌区域进行网格加密。对网格进行无关性验证，确定叶轮网格数量为90万，蜗壳网格数量为83万，整机计算域网格数量317万。

图6 整机网格及局部加密

图7 叶片和蜗舌边界层网格

4.2 计算方法

计算求解三维雷诺平均Navier-stokes方程，在FLUENT 15.0软件中分别采用S-A、Realizable κ-ε和SST κ-ω 3种湍流模型，速度-压力耦合采用SIMPLE算法求解，湍流耗散项、湍流动能和动量方程都采用二阶迎风格式离散；旋转坐标系设置为多参考系模型（MRF）；同时给定压力进口、压力出口边界条件；计算采用高阶精度进行迭代求解，收敛残差标准设为10-5；同时设置进出口的流量监测点，对每一步迭代下的流量监测，确保在满足残差收敛的前提下，监测点流量无明显波动；通过流量计算值与试验值对比，发现相对误差低于5%，验证数值模拟计算方法可行。

5 结果分析

5.1 风机性能对比

在同一转速为1175 r/min，针对风机全试验工况分别使用以上3种湍流模型进行定常流动的数值模拟，图8为3种湍流模型计算得到的风机静压与气动试验结果对比曲线。

从图中可知：3种湍流模型的模拟结果都与试验结果比较吻合。小流量工况下的静压计算值比试验值大，而大流量工况下的计算值比试验值小，曲线趋势总体一致；在大流量Q＞0.6 QBEP工况下，SST κ-ω更靠近试验值，S-A次之。而在流量Q＜0.6QBEP工况下，Realizable κ-ε模型与试验值更相符，但发现SST κ-ω和Realizable κ-ε在此区域存在不收敛的情况，鉴于此工况范围内流动的复杂性，对此范围内的气动性能预测，建议使用非定常做进一步验证。

总体上，3种湍流模型在外特性曲线的变化趋势总体一致，SST κ-ω模型在外特性计算中表现更好，S-A和Realizable κ-ε相差不大。

5.2 内部流场对比

为分析不同湍流模型对内流场的捕捉精度，现对风机流场的计算结果和PIV试验结果进行对比。

5.2.1 进口和蜗壳区域的流场分析

集流器进口截面A的速度分布和流线分别如图9，10所示。

图9 截面A速度分布

图10 截面A流线

图9（a）、10（a）分别为PIV试验测得集流器进口截面A时均速度分布及流线，从图中可以看出：在G工况点下，在进口右上方位置存在一个顺时针的旋涡。截面A的左下方为风机进口主流区域，此区域明显流动速度较大。图9（b）～（d）分别对应Realizable κ-ε、S-A 和SST κ-ω湍流模型条件下定常数值模拟结果的速度分布，图10（b）～（d）分别对应三者的计算流线。总体来说，数值计算预测的速度大小比试验结果大，速度分布及流线也与PIV试验结果比较符合，而且三者都捕捉到了旋涡，且旋涡位置与PIV试验结果相同。但详细对比可以发现，Realizable κ-ε、S-A模型的旋涡周围的速度梯度明显小于SST κ-ω模型，涡核周围流动呈现圆状，SST κ-ω涡核左上方存在一高速区域S1，且速度梯度大，流动呈椭圆状，造成其气流汇聚位置S2偏右下方，这与PIV试验结果更为吻合。

图11（a）为PIV试验测得蜗舌区域截面B的时均速度分布及流线，从图中可知，在Z2区域速度矢量向叶轮内偏斜，存在回流，且此区域内绝对速度较小；在主流区域Z1速度沿流向呈递减趋势，这符合蜗壳减速增压的规律。图11（b）～（d）分别对应Realizable κ-ε、S-A 和SST κ-ω湍流模型条件下的定常数值模拟结果，与试验结果相比，三者计算结果总体符合试验所测流动规律，但局部区域有所差异，SST κ-ω结果Z3区域速度梯度大，流场变化剧烈，明显看到蜗舌处回流多。S-A结果在主流区速度云图均匀过渡，流线分布均匀，蜗舌处回流较少。Realizableκ-ε流场分布情况介于二者之间。

图11 截面B速度分布及流线

5.2.2 进口和蜗壳区域的绝对速度分析

提取截面A上半径R1=35 mm、R2=70 mm、R3=95 mm圆（见图12）上的速度大小，绘制速度随θ=0～360°的变化曲线如图13所示。图13（a）表明：半径R1处绝对速度的模拟值约是试验值的2.8倍；在60°左右位置，试验值和模拟值都有极值出现，曲线趋势基本一致；在120°～360°区域，速度整体趋势变化平缓，3种湍流模型速度大小呈SST κ-ω＞S-A＞ Realizable κ-ε趋势。但发现SST κ-ω曲线在0～90°速度较其他曲线波动大；在300°～360°，曲线呈明显陡降趋势，这与PIV试验曲线吻合较好。图13（b）表明：S-A和Realizable κ-ε在整个区域内变化趋势较为接近，但在120°～240°和300°～360°区域内，SST κ-ω与试验曲线走势吻合更好。图13（c）表明：S-A和SST κ-ω整体变化趋势与试验曲线较为接近，Realizable κ-ε吻合较差，特别表现在0°～90°之间，这也是存在旋涡的位置，流场变化复杂。但是在300°～360°之间，SST κ-ω和PIV试验曲线都有一个陡增的趋势。

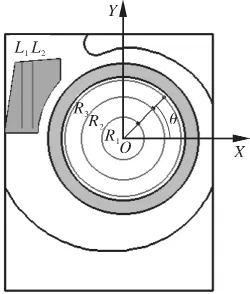
图12 半径R1，R2，R3及直线L1，L2于截面A的位置

图13 截面A上绝对速度沿半径R1，R2，R3分布规律

综上所述，3种湍流模型都捕捉到集流器进口右上方的旋涡；在模拟旋涡附近流场时，SST κ-ω和S-A模型表现更好，尤其SST κ-ω模型的模拟结果与试验结果在流动细节上吻合较好。

提取截面B上沿直线L1=100mm、L2=100 mm（图12）的绝对速度大小，绘制速度沿Y轴方向的变化曲线如图14所示。图14试验曲线表明：速度的模拟值和试验值存在一定差距，在主流区速度梯度总体上呈线性规律，在L=0～20 mm靠近叶轮的区域呈非线性规律，由叶轮与蜗壳的动静干涉作用引起；在L=90～100 mm靠近蜗舌的区域呈非线性规律，推测是由于流动受到蜗舌的影响。

图14 截面B上绝对速度沿L1，L2分布规律

从图14（a）、（b）对比可知：S-A和Realizable κ-ε对应L1，L2曲线上的速度分布趋势一致，说明S-A计算速度在蜗壳主流区和壁面附近的速度梯度变化一致，流场分布均匀；SST κ-ω对应L2曲线的倾斜程度明显大于L1，说明其计算速度在主流区的速度梯度大于壁面附近，流场变化剧烈；在同一条直线L1，L2上，SST κ-ω和S-A速度大小相差不大，Realizable κ-ε得到的速度明显小于前两者。

综上所述，蜗壳内主流区速度呈递减规律，流动向两侧移动；SST κ-ω能够较为准确预测蜗舌附近的流动分离，及蜗壳主流区速度变化规律，其它2种模型在蜗舌区域复杂流动的预测上表现一般。

6 结论

（1）对于多翼离心风机的静压，在大流量Q＞0.6QBEP工况下，3种湍流模型的性能预测均较为准确，无明显的偏差，SST κ-ω模型在外特性计算中预测精度最高，S-A和Realizable κ-ε相差不大。

（2）3种湍流模型都能捕捉到集流器进口右上方的旋涡；在旋涡附近速度梯度较大的区域，SST κ-ω和S-A表现更为突出，尤其SST κ-ω模拟结果与试验结果在流动细节上吻合较好，该湍流模型预测内部流场更为准确。

（3）SST κ-ω模型能够准确预测蜗舌附近的流动分离，及蜗壳主流区速度变化规律，其它2种模型在蜗舌区域复杂流动的预测上表现一般。

［1］ 郭鹏程. 水力机械内部复杂流动的数值研究与性能预测［D］. 西安：西安理工大学，2006.

［2］ 刘梅清，李秋玮，白耀华，等. 湍流模型在双吸离心泵数值模拟中的适用性分析［J］. 农业机械学报，2010，41（S1）：6-9.

［3］ 侯祎华，齐学义，张静，等. Spalart-Allmaras湍流模型在混流式长短叶片转轮流场计算中的应用［J］.水力发电学报，2010，29（1）：152-157.

［4］ Spalart P，Allmaras S. A one-equation turbulence model for aerodynamic flows［J］. La Recherche Aérospatiale，1992，439（1）：5-21.

［5］ Paciorri R，Dieudonne W，Degrez G，et al. Validation of the Spalart-Allmaras turbulence model for application in hypersonic flows［R］. AIAA97-2323，1997.

［6］ Chen X，Kim K Y，Kim S Y. Numerical simulation of three-dimensional viscous flow in a multiblade centrifugal fan［C］.ASME Fluids Engineering Division Summer Meeting. 1996.

［7］ 王嘉冰，区颖达. 集流器结构对多翼离心风机性能的影响［J］. 流体机械，2004，32（10）：22-25.

［8］ Wen X，Qi D，Mao Y，et al. Experimental and numerical study on the inlet nozzle of a small squirrel-cage fan［J］. Proceedings of the Institution of Mechanical Engineers Part A Journal of Power &Energy，2013，227（4）：450-463.

［9］ 何立博，姜涛，李志峰，等.多翼离心风机叶轮的正交设计与试验分析［J］. 流体机械，2016，44（6）：7-11.用研究［D］. 武汉：华中科技大学，2015.

［10］ 罗凯，罗鑫，黄闯，等. 基于 Fluent 的多翼式离心风机性能分析［J］. 流体机械，2014，42（7）：25-29.

［11］ 韩非非，席德科. 多翼离心风机数值计算及改进设计研究［J］. 机械科学与技术，2010，29（8）：992-996.

［12］ 周水清.低速风机内部非定常流动分离控制及应