夹带式散粮运输机垂直提升段力学模型探讨
马建宇,李永祥,王明旭,靳航嘉
(河南工业大学 机械工程学院,河南 郑州 450007)
随着国际贸易的日益发展,国际进出口贸易急剧增加,对大批量散料输送能力的要求越来越高,在港口的输运中更为显著[1]。相比于常规的大倾角运输设备如斗式提升机等,夹带式皮带机在运输过程中,物料被包裹在承重带与压带之间,不与外界接触,物料颗粒间无(或很小)相对运动,因此输运过程中振动小、物料的破碎率低、噪音低、无污染、无泄漏、无火花,不存在尘埃爆炸的隐患[2-3]。而且还拥有能耗低、绿色环保、经济性好、可靠性高、运输物料种类多等诸多优点。在当前我国港口码头的不断新建和扩建过程,对输送设备的需求越来越高的背景下,大输送量并且高效、节能的大倾角夹带式皮带运输机必将拥有广阔的应用前景[4]。
1 数学模型
1.1 夹带机提升段的一般数学模型
上世纪80年代,美国学者Dos Santos对大倾角夹带式皮带运输机进行了大量的理论研究,提出提升段的一般数学模型[5]。传统皮带机的运输倾角如果大于物料间的内摩擦角,带上的物料就会滑移引起运输失效。但夹带式皮带机相比传统的皮带机多了一条压带,压带靠自身的张力或外加压力压紧物料,增大了物料内部的摩擦力,物料被压带和承载带夹持,从而做到大倾角乃至垂直运输[6]。
对于无内聚力物料的受力,可以简化如图1所示(假设物料为紧密的平行层流)。
Wmsinα=(N+Wmcosα)μ
(1)
式中:α为输送角度;μm为夹持物料的内摩擦系数;μb为夹持物料与皮带摩擦系数;N为对覆盖带施加的压紧力;Wm为散装材料的重力;μ=min(μm,μb)。
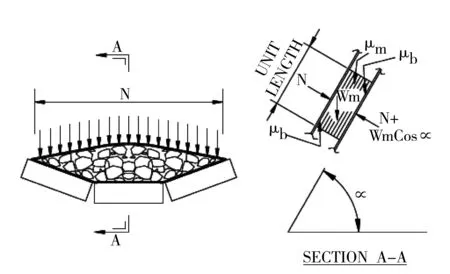
图1 夹带机提升段受力分析
由式(1)可得,夹带机为实现α°的倾斜角,对覆盖带施加的压紧力N,如式(2)。
(2)
如果承载带与覆盖带同步运行,可知:
Wmsinα=(2N+Wmcosα)μ
(3)
由式(3)可得,夹带机为实现α倾斜角,对覆盖带施加的压紧力N,如式(4)。
(4)
1.2 夹带机提升段的分析与改进模型
从理论上讲,夹带式皮带机仅仅依靠一组相对应的夹持托辊便可满足夹持要求。但在夹带机在实际工作中,两覆盖皮带不可避免的发生横向移动,可能会导致物料外泄。这就要求皮带必须向外伸出一定的“外沿”,并由“外沿”托辊施加一定的负载,保证物料始终处于被包裹夹持状态(如图2)。
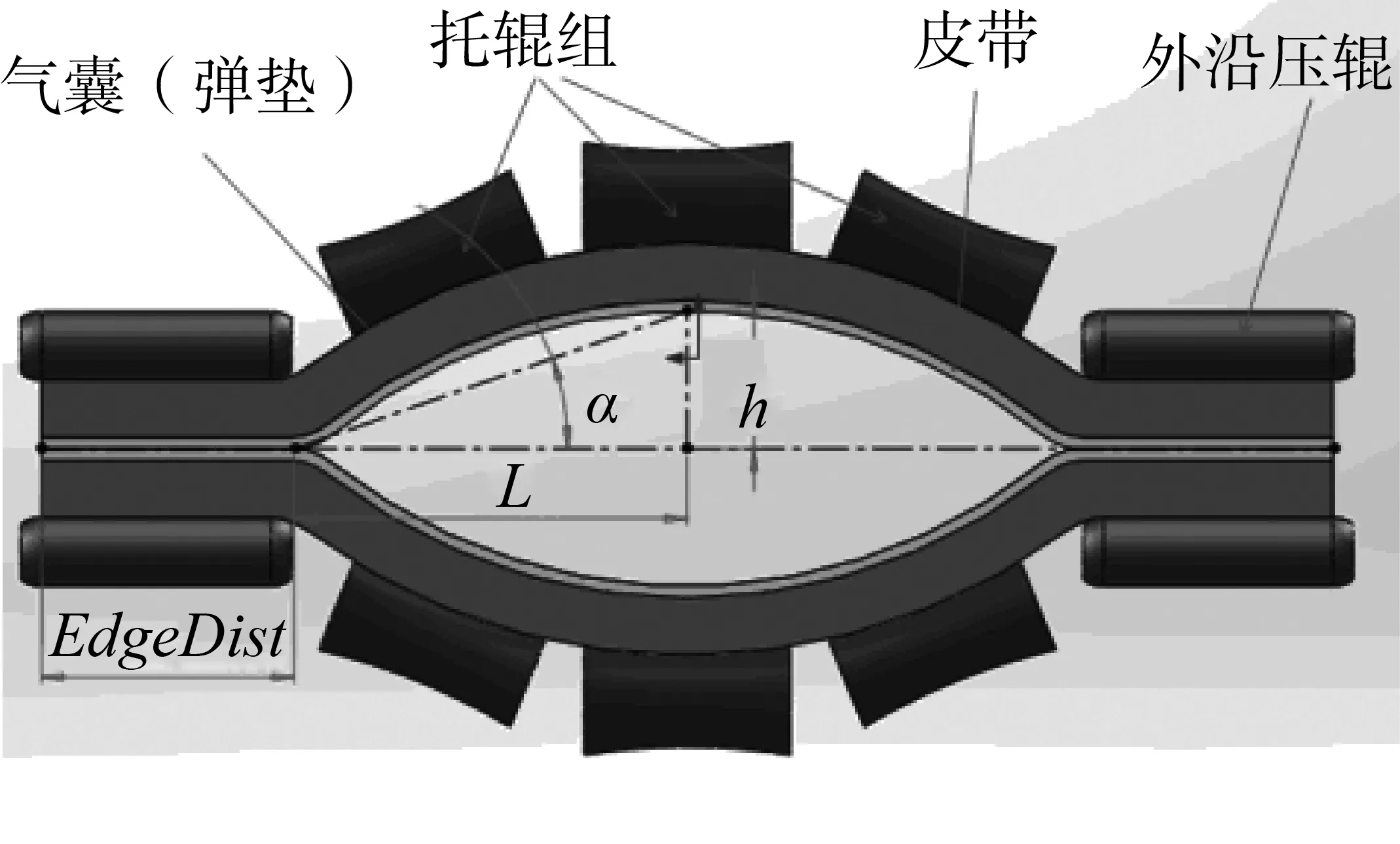
图2 夹带机夹持横截面示意图
因此夹带机提升段的一般数学模型在实际设计中有一定局限性,计算“外沿”的长度必须在一般模型的基础上做出相应改进,如图3。
图3 夹带机提升段受力分析的改进模型
其中的α、μm、μb、N、Wm含义同前文;Nm为N作用在承载带与物料的分量;Ne为N作用在“外沿”的分量;μe为两皮带间的摩擦系数。
当两带被同步驱动,必须施加在物料上以防止滑移的最小载荷Nm由式(4)可知:
(5)
如果仅仅承载带被驱动,则:
(min)Neμb=(min)Nmμ
(6)
于是,所需的最小总法向载荷N可以通过式(5)和式(6)联立表示:
(Min)N=(min)Ne+(min)Nm
(7)
也即:
(8)
如果承载带上的夹紧力按带宽均匀地分布在皮带上,则:
(9)
结合式(7)和式(9),便可以确定满足式(6)的每侧所需的“外沿”长度:
(10)
1.3 入料处到包料处长度与带速的函数关系
物料在被夹紧前,必须有足够的时间(距离)完成在承载带上的沉降并加速(或减速)到与带相同的速度。当物料稳定后,覆盖带必须在物料的上放被引入,并与承载带包络夹持物料。因此,物料的装载与夹持对皮带的速度的设计尤其重要。
设入料处到包料处长度为Lmin,带速为v0,物料团某一颗粒出入料口速度为vi,入料口倾斜角为θ,入料口到卸料处高度忽略不计(如图4),则:
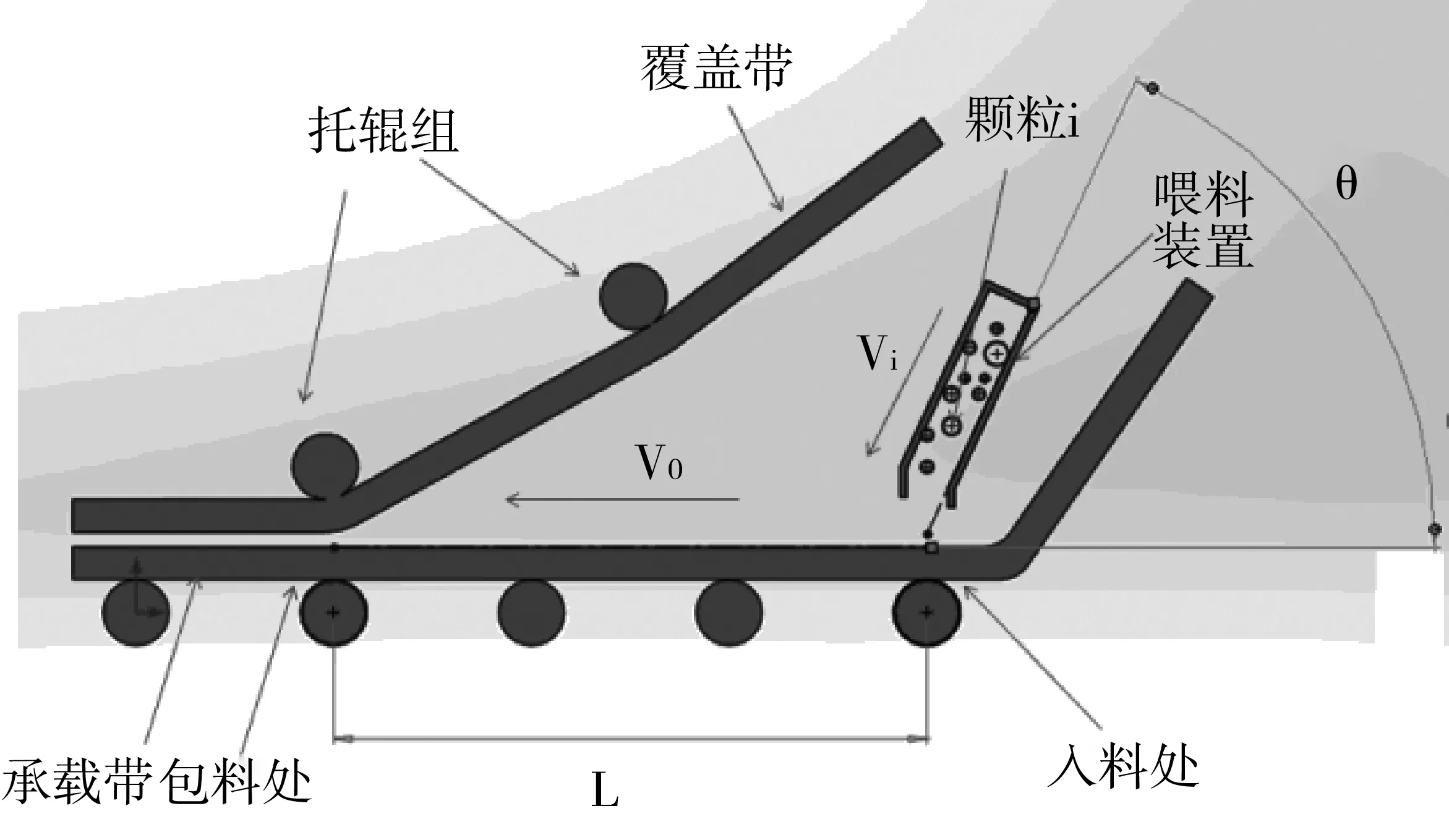
图4 入料处物料单颗粒受力分析

(11)
式中:g为重力加速度;μb含义同上文。
对式(11)变形,得:
(12)
每单个物料颗粒出入料口速度vi并不完全相同,但由于物料间颗粒相互碰撞产生功率消耗,因此计算时使用物料的平均速度代入式(12)推算入料处到包料处长度是合适的。
1.4 垂直提升段弹性散粒物料受力模型的推导
1.4.1 提升阶段物料的受力分析
将物料团单的单个颗粒分割开来,则在垂直提升阶段,物料团内任意颗粒i受到自身重力,以及相互间挤压产生的法向接触应力(不考虑切向力),根据牛顿第二定律,有:
(13)

Fni=-mig/μm
(14)
由式(4)及式(14)可知,任意颗粒在垂直提升阶段不“滑落”的基本条件为颗粒受到的由挤压力产生的摩擦力,要大于(至少等于)颗粒自身的重力。
1.4.2 皮带夹持宽度、弧度与压紧力的函数关系
在在一般情况下,物料与皮带的摩擦系数大于物料之间的,因此皮带与物料间的摩擦力本模型不作为考虑因素。公式(14)只是在理论上得出物料在垂直提升段所需的夹持力(压强),但由于散粒体“应力波”传递的不均匀性,根据文献[7],散状颗粒物料团在受压时,内部的受力呈现树状结构。对于某一被夹持物料团,不能简单的认为物料团的中心(质心)一定是受夹紧力最小的点。但当物料团厚度低于某一常数,受力最小点就是物料团的中心(质心)。文献[7]并没有给出这一常数的具体算法,也没有得出物料团中受力最小的颗粒与最外层压力的关系。笔者尝试利用赫兹(Hertz)接触理论,求得这一常数。
赫兹(Hertz)接触理论公式为:
(15)
式中:Fn为物料颗粒受到的法向接触力(挤压力);E*、R*为两接触颗粒的当量杨氏模量和当量半径,
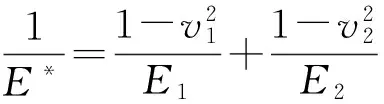
v、E、R、α分别是颗粒的泊松比、杨氏模量、半径、接触变形量。
对式(15)求导可得:
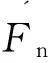
(16)
由高等数学理论可知,当α取得一个较小的变化量Δα(Δα可以取正或负),Fn的变化量ΔFn为:
(17)
假设受挤压力最小的颗粒受力为Fnmin,接触变形量为αmin,受力最大的颗粒(最外圈颗粒)受力为Fnmax,接触变形量为αmax,粮团堆叠层数为M层,则:
Fnmax=kFnmin
(18)
NFn=Fnmax-Fnmin
(19)
(20)
联立式(18)、(19)、(20)建立方程组即可得到在物料层数为M,物料团最外层与中心(质心)所受挤压力之间的关系。
2 垂直提升段力学模型的应用

小麦属于无粘连散粒体,由文献[9]可知,在被夹紧前,小麦散粮由输送机倾泻于夹带机运输带上,形成具有一定角度的堆积体,根据文献[10]与文献[11],小麦散粮堆积坡度角略小于小麦颗粒的最小摩擦角,取20°。为便于2个传送带夹紧,可知夹紧后(提升阶段)小麦粮团截面长轴与短轴两端点的夹角θ也应取20°,则粮团总厚度(截面短轴长度)为:
(1)当L≤1 130 mm时,h=Ltanθ=0.364L;
(2)当L>1 130 mm时,h=44 mm.
当L、h、θ确定,带弧长L1、夹带“外沿”长度、夹带夹持面横截面曲率半径R、面积S、也随之确定:
(21)
根据上文式(10),小麦散粮夹带垂直提升机夹带“外沿”长度选定为L1/3,则带宽L0
(22)
(23)
(24)
根据上文式(4),夹带机的气囊(弹垫)需要提供给粮团的夹持力为:
N=kS·k·S·H·ρ·g/μm
(25)
式(25)中:kS为总安全系数;H为气囊(弹垫)有效夹持长度;ρ为小麦容重;其它参数含义同上文。根据文献[12],取kS=1.3。
笔者初拟提升效率η=1 000 t/h,则:
η=ρSV
(26)
式(26)中:V为传送带的速度;其他符号含义同前文。
取小麦粮团截面长度L=1.2 m,单个气囊(弹垫)有效夹持长度H=0.1 m,满载厚度0.5 m,满载体积应变0.5。则根据本模型,夹带机各部件相应的参数如下:
小麦粮团夹持面截面高度0.44 m,面积0.379 m2;双侧气囊(弹垫)需提供988.1 N的压力,单侧气囊(弹垫)需提供3 759.1 Pa的压强,气囊(弹垫)当量体积模量7 518.0 Pa;皮带单侧“外沿”长度0.33 m,总带宽2.0 m;设定传送带的速度为1.0m/s,则本机构提升效率可达1 034.1 t/h,满足初拟提升效率的要求。
3 结论
利用现有的夹带机提升段的一般数学模型,获得了为防止夹带横向移动导致物料外泄的改进模型,如式(10),利用该改进模型可以求出夹带所需的“外沿”长度,如果μ=μe,则每侧所需的“外沿”长度约为1/4带宽度;如果所夹持物料属于粘性材料或细颗粒材料,则μe小于μ,当μe=μ/2时,则每侧所需的“外沿”长度约为1/3带宽度,以保证外加载荷力从承载带边缘转移到与覆盖带夹持物料的中心处。
借助牛顿经典力学,推导出入料处到包料处的长度的计算方法,式(12)。得出入料处到包料处的长度与颗粒与皮带间的摩擦系数、物料颗粒出入料口速度以及入料口倾斜角有关,与颗粒的质量、大小无关。
基于对赫兹接触定理公式求导,建立得到被夹持物料的层数(物料厚度)、物料最外层与中心(质心)所受挤压力之间关系的方程组,式(18)、式(19)和式(20)。利用该方程组可确定弹性散粒体垂直提升段夹持面跨度与夹持面高度之间的函数关系。仅需初拟设置跨度L便可求得物料垂直提升所需的夹持力(压强),对之前采用的槽式提升机相关设计公式和经验公式进行了改良,提高了计算的精度。并由此可进一步推导出电机功率、托辊的压力等参数,为具体压带机分部件的设计、研究、优化等做出一定的理论支撑,也可为其它相似的夹带式运输机提供研究思路和理论借鉴。
[1]张钺. 国内外带式输送机的应用概况[J]. 矿山机械,2001(5):55-60.
[2]熊康士. 我国垂直提升胶带机的前景[J]. 中州煤炭,1988(3):46-47.
[3]陈毅永. 垂直夹带输送机的关键技术[J]. 起重运输机械,1988(2):7-16.
[4]章崇任. 新型皮带机在建设工程中的应用[J]. 建筑机械化,1991(1):33-34.
[5]张挺. 有限空间大倾角提升设备选型综述[J]. 山西焦煤科技,2015(1):54-56.
[6]张书根. 大倾角下山施工时皮带输送机的应用与探讨[A]. 中国煤炭学会成立五十周年系列文集2012年全国矿山建设学术会议专刊(上)[C].中国煤炭学会煤矿建设与岩土工程专业委员会,2012:2.
[7]孙其诚,王光谦. 颗粒流动力学及其离散模型评述[J]. 力学进展,2008(1):87-100.
[8]许启铿,陈家豪,王录民. 小麦力学参数的三轴压缩试验研究[J]. 河南工业大学学报(自然科学版),2015(5):101-105.
[9]孟婷婷,周柏玲,石磊,田志芳. 杂粮粉与小麦粉粘度特性比较研究[J]. 粮油食品科技,2012(5):19-20.
[10]许志新. 小麦水分与容重变化的关系[J]. 粮油食品科技,2013(3):25-26.
[11]赵永志,江茂强,徐平,郑津洋. 颗粒堆内微观力学结构的离散元模拟研究[J]. 物理学报,2009(3):1819-1825.
[12]武文斌. 同步输送机的形式及设计[J]. 食品与机械,1994(3):22.●

