基于结构化低秩表示和低秩投影的人脸识别算法*

刘作军，高尚兵

(淮阴工学院计算机工程学院,江苏 淮安223003)

1 引言

人脸识别一直是计算机视觉及模式识别等领域研究的热点课题，它有很多实际的应用，比如视频监控、智能门禁、人机交互技术等。人脸图像有很高的维数，所以在识别前常常需要对图像进行降维。子空间学习方法，比如主成分分析[1]、线性判别分析[2]、局部保持投影[3]、边界Fisher分析[4]等成为人脸识别领域经典的方法。尽管子空间方法得到成功的应用，但它们对于图像污损(遮挡、伪装等)不具有鲁棒性。

近年来，基于稀疏表示分类SRC(Sparse Representation Classification)[5]的方法得到广泛研究。SRC方法的主要思想是将所有训练样本作为字典，得到测试样本在字典矩阵上的编码系数，然后通过最小残差法分类。SRC处理遮挡或随机像素破坏时在原始字典上添加了单位矩阵作为遮挡字典，这样可以很好地处理测试样本中存在的遮挡和像素破坏。然而，当样本维数比较高时，SRC的时间复杂度随之升高。为了解决这个问题，Yang等人[6]提取图像的Gabor特征，然后对遮挡部分进行字典学习，这样遮挡字典的规模会降低，加快了稀疏编码的速度。Ou等人[7]提出了遮挡字典学习方法，使得测试样本在原始训练样本矩阵和遮挡字典上的编码均是稀疏的，这样可以提升SRC方法的性能。Shi等人[8]提出使用L2范数来对表示系数进行约束，这样可以有效地处理高维数据(超过10 000维)。同样地，Zhang等人[9]提出协同表示分类CRC(Collaborative Representation based Classification)，指出是样本间的协同表示而不是L1范数约束提升了人脸识别的性能。CRC可以得到解析解，因此计算复杂度大大降低，并且可以取得和SRC相当的识别结果。

SRC及其改进方法的一个问题是它们要求训练数据是干净的，即不存在遮挡等情形，因此限制了它们在实际中的应用。最近的研究表明，视觉数据具有低秩结构，低秩矩阵恢复技术成为研究热点问题。Candès 等人[10]提出的鲁棒主成分分析RPCA(Robust Principal Component Analysis)可以从受噪声污染的观测数据中恢复出原始数据的低秩矩阵；随后Liu等人[11]提出了低秩表示LRR(Low Rank Representation)方法，RPCA可以看作是LRR的一种特殊形式。基于RPCA和LRR，研究者提出了很多方法来处理训练数据中存在的污损情形。胡正平等人[12]将RPCA恢复后的低秩矩阵和误差矩阵分别作为样本字典和遮挡字典。Wei等人[13]使用RPCA对原始训练样本进行低秩分解，得到干净的数据矩阵。另外，在RPCA的基础上引入了不相关项。Nguyen等人[14]将低秩表示用于人脸识别。受Fisher准则启发，张海新等人[15]提出了带有Fisher判别准则的低秩矩阵恢复算法，在有监督学习模式下对低秩矩阵进行恢复。Du等人[16]提出图正则化低秩稀疏表示恢复GLRSRR(Graph regularized Low Rank Sparse Representation Recovery)方法，GLRSRR在训练样本的表示系数上同时添加了低秩和稀疏约束，另外为了保持训练样本间的局部结构，GLRSRR引入了图正则项(最近邻图)，使得恢复后的训练样本具有很好的判别能力。Chen等人[17]提出了一种鉴别低秩表示方法，提升类间散布矩阵的不相关性，使得恢复后的不同类别的训练样本尽可能独立，因此测试样本可以用更多同类别的训练样本来表示。为了加快低秩分解后测试样本的分类，何林知等人[18]提出了基于RPCA和CRC的方法。

上述基于低秩矩阵恢复的人脸识别方法没有很好利用训练样本的类别信息，此外在得到原始训练样本的低秩矩阵后，通常会使用降维方法(如PCA或随机投影)对训练样本和测试样本进行降维。如果测试样本图像中存在遮挡，经过投影后这些因素也不能很好地消除。受归纳式RPCA IRPCA(Inductive RPCA)[19]的启发，本文在得到训练样本的恢复样本后，根据恢复样本和原始训练数据，得到低秩投影矩阵，提出了一种基于结构化低秩表示和低秩投影的人脸识别算法。首先通过结构化低秩表示得到恢复后的训练样本，根据恢复出的训练样本和原始训练样本得到低秩投影矩阵；然后利用低秩投影矩阵消除测试样本中可能存在的遮挡；最后使用SRC对恢复后的测试样本进行分类。在AR和Extended Yale B人脸库上的实验结果验证了本文方法的有效性和鲁棒性。

2 相关工作

假设X=[x1,x2,…,xn]∈Rm×n表示C类训练样本图像，共n幅，X的每列为一个样本图像，在本文中，也记为X=[X1,X2,…,XC]，其中Xi表示第i类训练样本，测试样本y∈Rm。SRC的目标函数为：

(1)

当得到系数α后，测试样本y可以通过最小残差法分类，即:

(2)

其中,αi是第i类对应的系数。

当训练样本中存在遮挡和像素破坏等情形时，SRC的性能急剧下降。为了解决这一问题，Liu等人[11]提出了低秩表示，可以有效地将异常像素和遮挡等从训练样本中剥离，LRR的目标函数如下：

s.t.X=AZ+E

(3)

其中,A为字典矩阵，Z为表示系数。式(3)可以通过不精确的增广拉格朗日乘子法求解。

3 基于结构化低秩表示和低秩投影的人脸识别

3.1 结构化低秩表示

SRC对表示系数添加了稀疏约束，但它没有考虑数据的子空间结构，而结构信息对于分类是必要的。LRR的理论表明，低秩可以揭示数据的子空间结构。因此，低秩稀疏表示[20]对表示系数同时添加低秩和稀疏约束，目标函数为：

s.t.X=AZ+E

(4)

假设Q=[q1,q2,…,qn]∈RK×n为样本的理想表示系数，其中样本xi的编码qi具有[0,…,1,1,1,…]T∈RK的形式,K为字典中原子个数，n为待表示样本个数。假设样本xi属于类别L，那么qi在DL上的编码均为1，其余全部为0。图1给出了Q的形式，这儿给出了来自3个类别的10个样本，其中x1,x2,x3属于类别1，x4,x5,x6,x7属于类别2，x8,x9,x10属于类别3，字典矩阵A有6个原子，每个类别分别有2个。

Figure 1 An example for Q图1 Q矩阵的示例

根据训练样本的类别信息，可以构造出具有块对角结构的矩阵Q，在低秩表示的过程中，将Q引入进来，得到如下的目标函数：

s.t.X=AZ+E

(5)

本文将训练样本作为字典矩阵，因此式(5)即为:

s.t.X=XZ+E

(6)

为了求解优化问题(6)，引入辅助变量W，则式(6)可以写成：

s.t.X=XZ+E,Z=W

(7)

式(7)对应的增广拉格朗日函数为：

L(Z,E,W,T1,T2,μ)=

‖Z‖*+β‖W‖1+λ‖E‖1+

(8)

其中,〈A,B〉=tr(ATB)，T1，T2为拉格朗日乘子，μ>0为惩罚参数。

本文利用含有自适应惩罚项的线性交替方向法LADMAP(Linearized Alternating Direction Method with Adaptive Penalty)[21]来优化式(8)，为描述方便，式(8)可以写成：

L(Z,E,W,T1,T2,μ)=

‖Z‖*+β‖W‖1+λ‖E‖1+

(9)

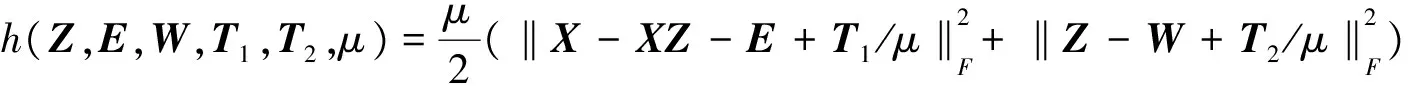
(10)

式(10)的解可以通过下式求解，即:

Zj+1=USVT=UTε[S]VT

(11)

其中,USVT是Ak的奇异值分解，Tε[S]是软阈值算子[22]。

变量W的更新过程如下：

(12)

变量E的更新过程为：

(13)

算法1总结了结构化低秩表示的求解过程。

算法1结构化低秩表示

输入：训练数据样本X=[X1,X2,…,XC]∈Rm×n，参数λ,β,α。

输出：(Z,W,E)。

若不满足终止条件，循环：

(1)根据式(10)更新Z；

(2)根据式(12)更新W；

(3)根据式(13)更新E；

(4)更新拉格朗日乘子:

(5)更新参数μ：μj+1=min(ρμj,μmax)；

(6)检查收敛条件:

‖X-XZj+1-Fj+1‖∞

‖Zj+1-Wj+1‖∞

输出(Z,W,E)。

3.2 低秩投影矩阵

虽然通过低秩矩阵恢复可以从原始训练样本中恢复出干净数据，但是如何处理测试样本中存在的遮挡仍是需要解决的问题。受文献[19]的启发，可以通过学习一个低秩投影矩阵，将受污染的测试图像投影到相应的低秩子空间。

从原始训练样本X=[x1,x2,…,xn]∈Rm×n获得一组主分量Y=[y1,y2,…,yn]∈Rm×n，其中稀疏噪声部分已被有效地去除。可以通过求解以下问题得到低秩投影矩阵。

s.t.Y=PX

(14)

假设P*为上述优化问题的最优解，则上述优化问题的最优解为P*=YX+,X+为X的伪逆矩阵，可以通过X+=VΣ-1UT求解，UΣVT为X的瘦奇异值分解。

3.3 本文算法流程

输入：C类训练样本X=[X1,X2,…,XC]∈Rm×n，测试样本y∈Rm，正则化参数λ、β和α，稀疏表示的参数srcλ。

(1)对所有训练样本通过算法1进行结构化低秩表示，即求解如下问题:

s.t.X=XZ+E

(2)得到训练样本的恢复数据Y=XZ*;

(3)计算低秩投影矩阵P*=YX+，其中X+为X的伪逆矩阵；

(4)测试样本y投影到相应子空间yr=P*y；

(5)计算Y的主分量W，W=PCA(Y)；

(6)训练样本恢复后的数据Y和测试样本恢复后的数据yr分别投影到W，即D=W(Y),yp=W(yr)；

4 实验结果与分析

本文在AR人脸库[23]和Extended Yale B人脸库[24]上进行人脸识别实验，以验证本文方法的有效性。为了更直观地表示本文算法的识别率情况，本文做了一些对比实验，包括NN(Nearest Neighbor)、LRC[25]、SRC[5]、CRC[9]、LRR_SRC[26]、LRSI[13]算法。训练样本和测试样本中均有遮挡或像素破坏，PCA用来对样本进行降维，SRC使用SolveDALM函数求解表示系数，正则化参数设为0.001。本文方法的参数β=15，λ=16，α=560。

4.1 AR人脸库上的性能分析

AR人脸库包括126个人超过4 000幅人脸图像。对于每一类人脸，26幅图像被分成了两个阶段。在每一阶段，每类有13幅人脸图像，其中3幅被墨镜遮挡的图像，3幅被围巾遮挡的图像，其余7幅为受到表情和光照变化的人脸图像。本文实验部分选取了50名男性和 50名女性共100类人脸图像。考虑以下三种情形来测试本文方法性能：

(1)Sunglasses：在该情形下，考虑训练样本和测试样本都受到墨镜遮挡的情形。墨镜大概遮挡了人脸图像的20%。本文选用第一阶段7幅无遮挡图像和1幅墨镜遮挡图像(随机选择)作为训练样本，第二阶段的7幅无遮挡图像和余下的墨镜遮挡图像(第一阶段的2幅和第二阶段的3幅)为测试样本，因此每类有8个训练图像和12个测试图像。

(2)Scarf：在该情形下，考虑训练样本和测试样本都受到围巾遮挡的情形。围巾大概遮挡了人脸图像的40%。本文选用第一阶段7幅无遮挡图像和1幅围巾遮挡图像(随机选择)作为训练样本，第二阶段的7幅无遮挡图像和余下的围巾遮挡图像(第一阶段的2幅加上第二阶段的3幅)为测试样本，因此每类有8个训练图像和12个测试图像。

(3)Mixed：在该情形下，考虑训练样本和测试样本都受到墨镜遮挡和围巾遮挡的情形。本文选用第一部分7幅没有遮挡图像，1幅墨镜遮挡图像(随机选择)以及1幅围巾遮挡图像(随机选择)作为训练样本，第二阶段的所有图像(7幅无遮挡图像，3幅墨镜遮挡图像，3幅围巾遮挡图像)和第一阶段余下的4幅遮挡图像(2幅墨镜遮挡图像和2幅围巾遮挡图像)为测试样本，因此每类有9个训练图像和17个测试图像。

在本实验部分，对比了各算法在维数为25、50、100、200和300时的识别性能，由于阶段1中含有3幅戴墨镜和3幅戴围巾图像，所以每种情形下各个算法重复3次，记录3次实验的平均值，如表1～表3所示。

Table 1 Recognition rate of differentmethods under sunglasses occlusion

从表1可以看到，本文算法在大多数维数下识别性能均优于其他算法(仅300维时稍低于CRC)；表2表明本文算法在维数较低时(25，50，100)性能明显优于其他对比算法；表3表明随着遮挡比例的增大，本文算法仍能取得较好的识别率。在上述三种遮挡情形下的实验结果验证了本文算

Table 2 Recognition rate ofdifferent methods under scarf occlusion

Table 3 Recognition rate of different methodsunder sunglasses and scarf occlusion

法的鲁棒性。

为了更直观地说明本文算法的有效性，图2和图3分别给出了部分原始训练样本图像和对应的低秩恢复图像，可以看出经过SLR分解后，表情变化、光照变化、遮挡等不利因素得到很好的去除，得到的干净数据字典有利于后面的稀疏表示分类。同时，图4和图5给出了部分原始测试样本图像和对应的经过低秩投影矩阵恢复后的图像，同样可以看到，通过将测试样本投影到对应的低秩子空间，测试图像中的表情变化、遮挡等因素得到较好的去除，这有利于后面的分类识别。

Figure 2 Some training images图2 部分训练样本图像

Figure 3 Recovered training images by SLR图3 结构化低秩表示恢复图像

Figure 4 Some test images图4 部分测试样本图像

Figure 5 Recovered test images by low rank projection matrix图5 低秩投影矩阵恢复图像

4.2 随机像素破坏下的识别性能

本实验使用Extended Yale B数据集，这个数据集包含38个人的2 414幅人脸图像，每人有59～64幅不同光照下的图像，图像大小为192×168。实验选择10%和20%的样本进行随机像素破坏，对于待破坏样本，随机选择10%的像素点，然后用均匀分布的值替换原始像素值，部分像素破坏后的样本图像如图6所示。然后每个类别随机选择一半作为训练样本，其余为测试样本，PCA维数为50、100和300。各个算法重复运行10次，记录其均值，如表4所示。

Figure 6 Some sample images after pixel corruption图6 部分像素破坏后的样本图像

算法维数(10%样本像素破坏)50 100 300维数(20%样本像素破坏)50 100 300NN58．7669．1276．7159．1868．4575．88LRC91．1593．7494．9991．8294．2495．24SRC88．0692．5795．6686．6491．0794．74CRC85．3194．9997．8386．9893．4197．66LRR＿SRC83．5692．7497．5883．1492．0796．41LRSI76．5490．5796．7476．7986．5694．32SLR＿LRP98．0098．0098．0095．9196．1696．24

从表4可以看出，本文算法在大多数情况下优于其他算法，这说明基于结构化低秩表示和低秩投影的方法对随机像素破坏具有一定的鲁棒性。

4.3 随机块遮挡下的识别性能

本实验在Extended Yale B数据集上进行，实验选择10%和20%的样本进行随机块遮挡，对于待遮挡样本，随机选择遮挡位置，然后用占原始图像10%大小的不相关图像对原始图像进行遮挡，部分块遮挡后的图像如图7所示。然后每个类别随机选择一半作为训练样本，其余为测试样本，PCA维数为50、100和300。各个算法重复运行10次，记录其均值，如表5所示。

Figure 7 Some sample images after random block occlusion图7 部分随机块遮挡后的样本图像

算法维数(10%样本像素破坏)50 100 300维数(20%样本像素破坏)50 100 300NN56．8467．5374．2156．5164．9471．62LRC88．7391．5792．8285．3189．3291．24SRC85．9890．6593．9183．6489．9893．57CRC83．5691．2496．6680．2291．6596．66LRR＿SRC80．5589．5796．1679．8091．1596．99LRSI74．6287．8197．1670．0387．3196．58SLR＿LRP98．0098．0898．0098．0898．3398．33

从表5可以看出，在维数比较低时，本文算法明显优于其他对比算法，随着遮挡样本比例的增加，本文算法一直能取得最高的识别率。比如在维数为50时，本文算法的识别率分别为98.00%和98.08%，比SRC算法分别提高了12.02%和14.44%;当维数为300维时，本文算法比LRSI算法分别提高了0.84%和1.75%，这表明本文算法对随机块遮挡具有较好的鲁棒性。

5 结束语

虽然SRC在测试样本存在遮挡和像素破坏的情况下取得了优异的识别性能，然而当给定的训练样本中存在遮挡和像素破坏时，SRC的性能会下降。为了解决这个问题，近年来低秩矩阵恢复方法得到了广泛研究，通过对样本进行低秩分解，可以得到样本的低秩矩阵。大多数低秩表示方法并没有有效利用训练样本的类别信息，同时，在对测试样本进行分类前，没有考虑测试样本中存在的遮挡和像素破坏。为了充分利用训练样本的类别信息和去除测试样本中存在的遮挡和像素破坏，本文提出了基于结构化低秩表示和低秩投影的人脸识别算法。结构化低秩表示通过引入样本的理想编码正则项，使得同类别样本的表示尽可能相似，这样很好地保留了样本的结构信息。同时根据原始训练样本和恢复后的训练样本得到低秩投影矩阵，通过将测试样本投影到该低秩投影矩阵，可以很好地去除测试样本中存在的遮挡和像素破坏，实验结果表明本文算法具有很好的鲁棒性。

本文算法在训练样本充足的情况下可以取得较好的识别结果，然而单训练样本在实际应用中经常遇到，如何将本文算法扩展到单训练样本人脸识别，将在后续的工作中进行研究。

[1] Turk M, Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.

[2] Belhumeur P N,Hespanha J P,Kriegman D.Eigenfaces vs.fisherfaces:Recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[3] He X,Yan S,Hu Y,et al.Face recognition using Laplacianfaces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.

[4] Yan S,Xu D,Zhang B,et al.Graph embedding and extensions:A general framework for dimensionality reduction[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(1):40-51.

[5] Wright J,Yang A Y,Ganesh A,et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):210-227.

[6] Yang M,Zhang L,Shiu S,et al.Gabor feature based robust representation and classification for face recognition with Gabor occlusion dictionary[J].Pattern Recognition,2013,46(7):1865-1878.

[7] Ou W,You X,Tao D,et al.Robust face recognition via occlusion dictionary learning[J].Pattern Recognition,2014,47(4):1559-1572.

[8] Shi Q,Eriksson A,Van Den Hengel A,et al.Is face recognition really a compressive sensing problem?[C]∥Proc of IEEE Conference on Computer Vision and Pattern Recognition,2011:553-560．

[9] Zhang L,Yang M,Feng X.Sparse representation or collaborative representation:Which helps face recognition?[C]∥Proc of the IEEE 13th International Conference on Computer Vision,2011:471-478．

[10] Candès E J,Li X,Ma Y,et al.Robust principal component analysis?[J].Journal of the ACM,2011,58(3):11.

[11] Liu G, Lin Z, Yan S,et al.Robust recovery of subspace structures by low-rank representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(1):171-184.

[12] Hu Zheng-ping,Li Jing.Face recognition of joint sparse representation based on low-rank subspace recovery[J].Acta Electronica Sinica,2013,41(5):987-991.(in Chinese)

[13] Wei C,Chen C,Wang Y.Robust face recognition with structurally incoherent low-rank matrix decomposition[J].IEEE Transactions on Image Processing,2014,23(8):3294-3307.

[14] Nguyen H V, Huang R,Yang W,et al.Face recognition based on low-rank matrix representation[C]∥Proc of the 33rd Chinese Control Conference,2014:4647-4652.

[15] Zhang Hai-xin, Zheng Zhong-long, Jia Jiong,et al.Low-rank matrix recovery based on Fisher discriminant criterion[J].Pattern Recognition and Artificial Intelligence,2015,28(7):651-656.(in Chinese)

[16] Du H,Zhang X,Hu Q,et al.Sparse representation-based robust face recognition by graph regularized low-rank sparse representation recovery[J].Neurocomputing,2015,164(C):220-229.

[17] Chen J,Yi Z.Sparse representation for face recognition by discriminative low-rank matrix recovery[J].Journal of Visual Communication and Image Representation,2014,25(5):763-773.

[18] He Lin-zhi,Zhao Jian-min,Zhu Xin-zhong,et al.Face recognition algorithm based on low-rank matrix recovery and collaborative representation[J].Journal of Computer Applications,2015,35(3):779-782.(in Chinese)

[19] Bao B K,Liu G,Xu C,et al.Inductive robust principal component analysis[J].IEEE Transactions on Image Processing,2012,21(8):3794-3800.

[20] Du H,Hu Q,Qiao D,et al.Robust face recognition via low-rank sparse representation-based classification[J].International Journal of Automation and Computing,2015,12(6),579-587.

[21] Lin Z,Liu R,Su Z.Linearized alternating direction method with adaptive penalty for low-rank representation[C]∥Proc of the 2011 Neural Information Processing Systems Conference,2011:612-620.

[22] Lin Z,Chen M,Ma Y.The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[J].arXiv preprint arXiv:1009.5055,2010.

[23] Martinez A M.The AR face database[R].Cerdanyola del Valles:Autonomous University of Barcelona,1998.

[24] Georghiades A S,Belhumeur P N,Kriegman D J.From few to many:Illumination cone models for face recognition under variable lighting and pose[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(6):643-660.

[25] Naseem I,Togneri R,Bennamoun M.Linear regression for face recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(11):2106-2112.

[26] Du Hai-shun, Zhang Xu-dong, et al, Hou Yan-dong.Face recognition method based on low-rank recovery sparse representation classifier[J].Computer Science,2014,41(4):309-313.(in Chinese)

附中文参考文献：

[12] 胡正平,李静.基于低秩子空间恢复的联合稀疏表示人脸识别算法[J].电子学报,2013,41(5):987-991.

[15] 张海新,郑忠龙,贾泂,等.基于Fisher判别准则的低秩矩阵恢复[J].模式识别与人工智能,2015,28(7):651-656.

[18] 何林知,赵建民,朱信忠,等.基于低秩矩阵恢复与协同表征的人脸识别算法[J].计算机应用,2015,35(3):779-782.

[26] 杜海顺,张旭东,侯彦东,等.一种基于低秩恢复稀疏表示分

类器的人脸识别方法[J].计算机科学,2014,41(4):309-313.