单排桩-承台-联系梁组合基础受力分析

张林涛

(西安铁一院工程咨询监理有限责任公司,西安 710065)

在房屋工程设计中，因相邻建筑基础或工艺布置等诸多因素的影响，桩基及承台无法按常规形式布置，导致柱(墙)下桩基础设置成单排桩的基础形式。由于单排桩的弱轴方向无法有效传递柱底弯矩，需在单排桩与相邻基础间设置刚性联系梁，形成“单排桩-承台-联系梁”的组合基础形式，共同承担上部荷载。典型的组合基础形式如图1所示。

联系梁是组合基础间相互作用、协同变形的重要结构构件，对加强基础间的整体性和调整基础间的不均匀沉降都起到了十分重要的作用[1-3]。因此，“单排桩-承台-联系梁”组合基础设计的重点和难点就是联系梁受力模式的合理确定。

图1 典型组合基础形式

目前，联系梁的受力模式一般认为有以下几种情况：(1)平衡柱底弯矩，其分担弯矩按联系梁的线刚度进行分配；(2)承担地震作用产生的轴向拉力，拉力值取两柱轴向压力较大者的1/10；(3)承担联系梁上填充墙体的荷载。传统设计中，往往按(1)、(3)或(2)、(3)二种组合工况进行设计。

(1)、(3)组合是根据《建筑桩基设计规范》(JGJ94—2008)第4.2.6条相关规定执行的，据此设计的联系梁未考虑单排桩弱轴方向的弯矩，计算结果偏于不安全；(2)、(3)组合是根据文献[4]执行的，据此设计的联系梁梁端弯矩较大，计算结果又偏于保守，很不经济。因此，对于“单排桩-承台-联系梁”组合基础而言，上述两种联系梁的计算模式都有不妥之处，主要的问题有：(1)未考虑“单排桩-承台-联系梁”的整体效应所导致的柱底弯矩分配；(2)未考虑“桩-土效应”的影响；(3)尚不能考虑基础不均匀沉降产生的附加弯矩影响。

基于此，拟建立“单排桩-承台-联系梁”一体化模型，对影响组合基础受力的联系梁刚度、基础不均匀沉降进行理论分析，找出相互影响关系。为了便于工程应用，拟建立有限元模型，通过“桩-土效应”来反映桩基和联系梁的组合刚度关系，并以强迫位移荷载的方式考虑基础不均匀沉降的影响，联系梁的受力可从模型中直接读取。

1 联系梁的刚度要求

1.1 现行规范要求

联系梁要在组合基础中协调两侧基础的内力并分担柱底弯矩和剪力，就需要具有一定的刚度。参照《建筑桩基技术规范》(JGJ94—2008)，联系梁的截面高度取柱中心距的1/10～1/15，且不应小于400 mm，梁宽度可取高度的1/2～1/3，且不应小于250 mm。上述规定给出的联系梁截面取值范围较大，且未考虑上部结构与基础的刚度关系，仅对抗震构造要求设置的联系梁[5-6]有参考价值。

1.2 组合基础中联系梁刚度要求

对于混凝土灌注群桩基础，群桩承台的抗弯刚度为

(1)

式中，ri为第i根桩的中心至基础底面形心回转轴的距离，m；kpc为单桩抗压刚度，可通过p-s曲线试验确定，亦可由下式计算

kpc=∑CpcApc+CpzAp

(2)

式中，Cpc为桩周各土层的当量抗剪刚度系数，kN/m3；Apc为各层土中的桩周表面积，m2；Cpz为桩间土的当量抗压刚度系数，kN/m3；Ap为桩的截面积，m2。

根据相关文献[7-8]，满足上部结构柱脚固接的基础刚度条件为：柱脚抗弯刚度不小于对应柱抗弯线刚度的16倍，即

Km/Kc≥16

(3)

当组合基础中单排桩的弱轴方向存在一定弯矩和剪力时，按桩顶与承台的连接为铰接的基本假定，桩基础是无法传递弯矩的。此时，单排桩与相邻多桩承台基础间设置有刚性联系梁，可考虑较强刚度基础对较弱基础的刚度贡献，上式可变为

(Km1+Km2+Kl)/(Kc1+Kc2)≥16

(4)

式中，Km1为单排桩弱轴方向的抗弯刚度，根据假定可视为0 kN/m；Km2为相邻多桩承台的抗弯刚度；Kl为联系梁的抗弯刚度；Kc1、Kc2为与承台相连的上部竖向构件的抗弯刚度。

1.3 基础不均匀沉降对联系梁的刚度影响

在实际工程中，由于相邻基础的不均匀沉降导致的联系梁内力变化是客观存在的，特别是针对高填方区，基础间的不均匀沉降很难避免，有时甚至是联系梁设计的控制因素。在组合基础中，基础不均匀沉降、联系梁刚度和联系梁内力三者间是相互关联的。

文献[8]给出了基础及联系梁刚度与不均匀沉降间的本构关系，可以通过基础的不均匀沉降值确定基础所受的协变内力，其表达式如下

{P}={Kd+K}{ω}

(5)

式中，{P}为联系梁的内力值；{Kd+K}为基础及联系梁的组合抗弯刚度；{ω}为基础间沉降差。

2 组合基础计算模型的建立

结合1.2、1.3条，单排桩基础与联系梁的组合刚度矩阵{Kd+K}与联系梁截面、桩基截面及桩侧土层约束均有关，直接根据地质条件来确定组合刚度难度很大。即使得到了单排桩基础与联系梁的组合刚度，还得考虑相邻多桩承台的刚度影响，其计算公式繁杂，不便于工程设计。基于此，采用大型有限元软件SAP2000建立“单排桩-承台-联系梁”有限元模型[9-10]，模型通过“桩-土效应”来反映桩基和联系梁的组合刚度关系，并以强迫位移荷载的方式考虑基础不均匀沉降的影响。该方法可更为准确地计算联系梁的截面和配筋，为类似工程提供设计参考。

2.1 有限元模型的建立

SAP2000模型中，承台采用厚壳单元、桩及联系梁采用框架单元，线单元和实体单元间采用节点耦合进行连接。桩基顶与承台的连接按固接铰设置，沿桩长将桩基划分成若干单元，每一单元节点处设置桩侧土弹簧来模拟“桩-土效应”，弹簧刚度可按2.2节确定；柱底反力按上部结构实际受力输入，组合基础间的不均匀沉降值以强迫位移的荷载形式施加，不均匀沉降值按2.3节确定。

2.2 桩-土效应[11-13]

桩在剪力以及弯矩作用下将会产生水平位移及转角，从而使桩身挤压桩侧土体，桩侧土必然对桩产生横向抗力。桩-土作用实质上是桩身内力与变形关系，这种关系体现出一种极其复杂的非线性。为了便于计算，设计中常采用线弹性法进行分析，即在一定桩顶位移内采用“m”法，“m”法确定的土弹簧刚度为

(6)

式中，m0为土体地基抗力系数；b0为桩身有效作用宽度；z为计算点距桩顶的竖向距离；h为土弹簧代表的土体高度。

为简化计算，以土弹簧位置处的地基系数近似代替土弹簧所代表的土体地基系数，于是式(6)可简化为

Ki=Kmi=mobozih

(7)

根据公式(7)，将桩沿其桩长划分为若干单元，在每个桩单元节点两侧设置受压弹簧(简称土弹簧)，每个土弹簧模拟该处节点上、下单元各一半范围内土体对桩身的水平作用。以此建立的力学模型更为真实地反应桩基与周围土的相互作用关系。

2.3 基础不均匀沉降

《建筑桩基技术规范》(JGJ94—2008)中规定，相邻桩基础间的不均匀沉降限值为0.002l0，而在实际工程中，在满足上部结构竖向荷载承载力的前提下，相邻桩基础的不均匀沉降量较规范允许值要小，其值与桩基所处的地质条件有关。依据以往工程经验，相邻基础沉降差可取规范限值的0.4～0.7倍。对于具体工程设计，沉降差值宜按竖向荷载所计算的实际沉降差进行计算。

3 工程算例

3.1 工程概况

某铁路客车段生产调度指挥中心办公综合楼，建筑总高度14.4 m，共4层，为内走廊式建筑，呈长方形平面布置。结构纵向标准柱距9.0 m，横向柱距为7.5 m+2.4 m+7.5 m。当地的抗震设防烈度为7度，设计基本地震加速度为0.10g，设计地震分组为第二组，地震动反应谱特征周期为0.40 s。建筑结构的抗震设防分类为乙类，安全等级为二级，结构重要性系数1.0。

根据勘察报告，地层岩性自上而下依次为：

(1)人工填土，层厚0.5～1.2 m，站场新填土；

(2)粉质黏土，硬塑，层厚1.0～2.0 m，成分以黏粒为主，土质不纯；

(3)细砂，浅黄色、灰黄色，呈夹层及透镜体状分布于粉土中，厚度1.5～5.5 m，成分以石英、长石为主，为中间夹层；

(4)粗砂，灰黄色，拟建场地下部主要地层，层厚12.0～24.0 m，成分以石英、长石、云母为主，砂质较纯，密实。

本工程桩基设计等级为丙级，桩基础的环境类别为Ⅱ-b类，采用钻孔灌注桩，桩径0.6 m，粗砂层为桩端持力层。受房间内设备基础布置的影响，角部框架柱只能布置成单排桩形式，此时与相邻基础间设置联系梁以形成组合基础，以平衡单排桩弱轴方向的弯矩，组合基础平面布置如图2所示。

图2 组合基础平面布置(单位：mm)

假定柱底完全嵌固，嵌固点为承台顶，此时上部结构计算所得的角柱柱底反力见表1。

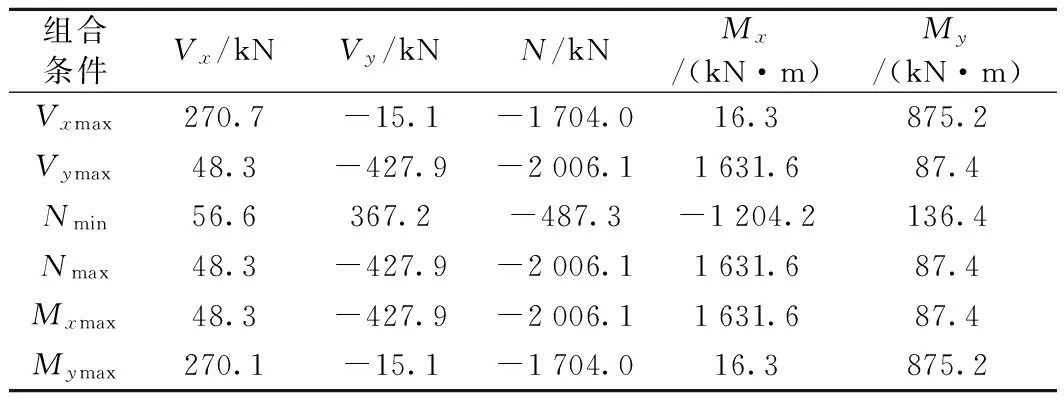
表1 柱底反力

3.2 常规设计

按《建筑桩基技术规范》(JGJ94—2008)确定的联系梁截面取350 mm×800 mm，此时联系梁梁内轴力N=Max{Vxmax，0.1Nmax}=270.7 kN，考虑梁上墙体线荷载产生的梁端弯矩M=150.0 kN·m。按纯弯构件计算时梁端上部钢筋面积为804 mm2(忽略轴压力的有利作用)；按拉弯构件计算时梁端上部钢筋面积As=1 400 mm2。

按文献[4]，桩端与承台间连接视为铰接，单排桩弱轴方向的柱底弯矩由联系梁承担，联系梁截面仍取350 mm×800 mm，此时联系梁梁内轴力仍为270.7 kN，梁端弯矩为(875.2+150)kN·m=1025.2 kN·m。按纯弯构件计算时梁端上部钢筋面积为5 200 mm2(忽略轴压力的有利作用)；按拉弯构件计算时梁端上部钢筋面积As=5 890 mm2。

由此可见，按《建筑桩基技术规范》(JGJ94—2008)执行时，其计算值偏小，而按文献[4]执行时，计算结果又偏于保守，梁的配筋率远远超出规范限值，需加大截面重新设计。因此，上述两种设计方法都有不妥之处，且均未考虑基础不均匀沉降的影响。

3.3 “单排桩-承台-联系梁”一体化模型设计

根据前文所建立的“单排桩-承台-联系梁”一体化模型如图3所示。

图3 组合基础有限元模型

模型中各项参数及假定如下。(1)模型中桩径及承台截面按实际尺寸输入，联系梁截面满足公式(4)的要求。(2)根据地质勘察报告，场地地层自上向下主要由人工填土、粉质黏土层、细砂层及粗砂层组成。考虑承台埋深，桩基深度范围内土层为细砂层和粗砂层。细砂层的地基抗力系数为100 000 kN/m4，粗砂层的地基抗力系数为250 000 kN/m4，按公式(7)可计算出不同深度的桩侧土弹簧刚度；(3)为了便于结果对比，考虑基础不均匀沉降工况时，相邻基础沉降差取规范限值的0.5倍，并以强迫位移荷载施加到模型中。

“单排桩-承台-联系梁”一体化模型计算的联系梁梁端最大内力及相应配筋面积如表2所示。

表2 联系梁最大内力值及配筋

从表2数据分析可见，不考虑基础不均匀沉降影响时，采用“单排桩-承台-联系梁”一体化模型的计算值介于规范和文献[4]的计算值之间， 计算结果更趋于合理；考虑基础不均匀沉降时，采用“单排桩-承台-联系梁”一体化模型的计算结果较规范和文献[4]的计算值都要大，说明基础不均匀沉降对联系梁的受力影响很大，特别是对于高填方区的单排桩基础，其影响更不容忽略。

值得说明的有两点：(1)表2中计算值是基于上部结构完全嵌固于承台顶得到的，若考虑上部结构-基础协同作用时[14-15]，计算值会进一步优化，其结果更合理；(2)表2中考虑基础不均匀沉降的计算结果是基于相邻基础沉降差为规范限值0.5倍得出的，对于具体工程，建议按竖向荷载所计算的实际沉降差值进行计算。

4 结论

通过对“单排桩-承台-联系梁”一体化模型的理论和有限元模拟分析，得出以下结论。

(1)通过建立“单排桩-承台-联系梁”一体化模型，可以充分考虑联系梁、相邻基础刚度及相邻基础不均匀沉降的影响。

(2)借助SAP2000有限元模型，通过“桩-土效应”可综合反映桩基和联系梁的组合刚度，并以强迫位移荷载的方式考虑基础间不均匀沉降的影响，真实反映了“单排桩-承台-联系梁”的受力状态。

(3)工程算例结果表明，“单排桩-承台-联系梁”一体化模型设计方法具有较强的可行性和合理性，可避免传统设计中联系梁设计过于保守或偏于不安全的弊端。

[1] 谢云飞，李琪.群柱下联合桩承台空间桁架传力机理的探讨分析[J].特种结构，2009，26(4)：80-82.

[2] 郭盛，武汉站联合桩基设计研究[J].铁道工程学报，2010(2)：98-101.

[3] 李静，盛晓杰，论RC基础联系梁设计[J].四川建筑，2012，32(6):108-109.

[4] 夏宏君，张兰春.基础系梁对相邻基础的弯矩调节作用研究[C]∥中国电机工程学会电力土建专委会结构分专委会学术研讨会论文集，2006：86-89.

[5] 中华人民共和国住房和城乡建设部.GB 50011—2010 建筑抗震设计规范[S].北京:中国建筑工业出版社，2010.

[6] 朱炳寅，建筑抗震设计规范应用与分析[M]，北京：中国建筑工业出版社，2015.

[7] 中华人民共和国住房和城乡建设部.JGJ 94—2008 建筑桩基技术规范[S].北京:中国建筑工业出版社，2008.

[8] 毕征，许金余，马波.柱下独立基础连系梁的设计计算探讨[J].工程力学，2001(S)：679-683.

[9] 田堃，朱杰江.基于SAP2000考虑上部结构与基础共同沉降计算研究[J].结构工程师，2015，31(1)：99-104.

[10] 鲍鹏，王梦.超长桩基础抗震性能有限元分析[J].河南大学学报(自然科学版)，2014，44(3)：360-363.

[11] 李铁柱.桩-土作用在大型旅客站房基础设计中的应用[J].铁道标准设计，2014，58(2)：117-121.

[12] 王春，王宏东.桩-土作用模型在桥梁设计中的研究与应用[J].工程与建筑，2007，21(5)：770-772.

[13] 王羽，柴贺军，吴袓松，等.基于桩-土作用效应的组合式抗滑桩结构研究[J].重庆交通大学学报(自然科学版)，2014，33(1)：90-93.

[14] 吴浩，杨卓，张文强，等.上部结构-地基基础协同作用分析及设计优化[J].施工技术，2015(S2)：45-49.

[15] 张曼，曾长女，田文礼.粉土地区上部结构与地基基础共同作用有限元分析[J]岩土工程学报，2013(S1)：462-467.