大跨径拱桥缆索施工支架非线性受力特性分析

施 洲,张晓珂

(西南交通大学土木工程学院,成都 610031)

自2001年中国第一座铁路钢管混凝土拱桥建成以来，在大跨度铁路拱桥中，钢管混凝土结构越来越多地被应用。随着跨径的增大，钢管拱桥拱肋的架设成为施工中的关键，无支架缆索吊装施工可依次吊运拱肋节段并安装到位，解决了地势险恶及场地狭小等难题，近年来被广泛应用[1-3]。如湖北株归龙潭河大桥、重庆巫山巫峡长江大桥、湖南南县茅草街大桥，因此施工过程中塔架的安全性尤为重要，但由于缆索的受力采用各种理论简化方式计算，造成施工塔架的受力计算不够精确[4]。

国内已对缆索吊施工中塔架的受力进行了大量的研究，目前缆索吊缆索的计算通常是按照文献[5]中的公式计算，且已在巫山长江大桥、合江长江一桥等大桥中应用。这种方式便于施工单位掌握，能够指导施工但相对繁琐。此外陈俊松，刘飞利用静力平衡方程，并假定主索的线形为抛物线，提出一种主索受力和变形的简易计算方法[6]，但是这种主索线形简化处理仅在一些简易的缆索吊装工程能够适用。郭常瑞、卞佳等对主索系统创立了静力平衡方程和迭代计算方程，计入主索滑移的影响[7]，但随着跨度的增加，缆索几何非线性及滑移影响也将增大，需要对缆索施工体系进行精确模拟[8-10]。

目前对于施工塔架的具体计算都比较完善，将吊塔与扣塔分离建模，对塔架强度、刚度及稳定性都做了大量分析。在设计及计算拱肋线形时，通常不计扣塔对主拱线形的影响，其仿真模型按照扣索顶端固结计算，这与实际是不符的，在吊装过程中，扣锚索的不平衡水平力和作用在扣塔上的风荷载必然引起扣塔产生顺桥向偏位，使拱肋安装线形发生改变，扣索顶部固结的处理方式得到的安装线形与实际施工时相比有偏差。

通过有限元计算分析及文献[5]中的解析法两种方法对缆索施工体系进行受力分析，有限元计算中考虑了主索的滑移及吊塔的偏位，通过主索的几何非线性分析得到更为精确的主索及施工塔架的变形及内力结果。

1 桥梁及缆索施工支架概况

本文计算桥梁为某铁路中承式钢管混凝土提篮拱。桥位处地貌属于堆积高山峡谷区，多年平均风速1.6 m/s，最大风速为31 m/s，地理环境复杂，风载对缆索吊施工影响较大。桥梁跨度430 m，结构形式新颖，采用拱脚与墩台分离构造，为同类型桥梁跨度之最。线路左右侧拱肋平面内矢高为112 m，矢跨比为1∶3.84，拱轴线采用悬链线，拱轴系数为2.1。

该桥采用缆索吊机配合斜拉扣挂法悬臂架设，分为缆索吊机系统及扣锚索系统，拱肋一共分14段安装(两岸对称)，2号～9号节段重2 500 kN，10号～14号节段重1 500 kN。施工塔架包括吊塔与扣塔两部分，吊塔底部铰接在扣塔上，顶部支承缆索体系。两侧吊塔结构相同，高度为20.5 m，顺桥向宽4 m，横桥向宽39 m；两侧扣塔高度悬殊，西侧上游扣塔高149.5 m，下游扣塔高128.5 m；东侧上游扣塔高24.7 m，下游扣塔高4.7 m。两侧扣塔顺桥向均宽12 m，横桥向均宽39 m。塔架均为由万能杆件拼接而成的桁架结构，桥梁整体布置及缆索施工体系示意如图1所示。

2 模型建立

2.1 吊塔及主索系统仿真模型

采用空间有限元软件Midas对塔架系统上部的吊塔及缆索进行建模分析，两侧吊塔部分相同，高20.5 m。吊塔杆件选用梁单元模拟，揽风索选用索单元模拟，模型共389个节点，669个单元。吊塔铰接于扣塔塔顶，因此吊塔底部约束按完全铰接处理。

图1 桥梁整体布置及缆索施工体系示意(单位：m)

缆索吊机横桥向设置2组主索及配套的起重索和牵引索等，缆索主跨610 m，西侧边跨165 m，东侧边跨89 m。为简化计算，忽略起重索和牵引索对主索的影响[11]，选用只受拉索单元模拟主缆，由于主索跨径较大，垂度效应不可忽略，且吊重过程中主索将发生大变形，需要考虑主索的几何非线性影响，在Midas中选择考虑大位移的非线性分析计算主索线形。由于缆索吊施工过程中主索滑移量最大达到近60 cm，必须考虑主索滑移的影响。经多次试算，模型中将主索与吊塔间鞍座结构简化为刚度较小的主索截面梁单元，此连接单元高度1.2 m，通过释放与吊塔连接处的梁单元转动约束来近似模拟索鞍大角度转动的非线性位移效果，即主索的滑移，如图2所示。最后通过悬索桥分析控制精确找平得到主缆线形。将吊重作为集中力作用至主索，并计入风力的影响，改变主索与塔架相对位置和集中力在主索上的作用点位置，可模拟吊装任一节段拱肋在主索任意位置对主索及施工塔架的影响。

图2 主索滑移模拟示意(单位：m)

2.2 扣塔及主桥模型建立

采用Midas软件对扣塔系统及主桥建立空间有限元模型，扣塔、主梁和拱肋均选用梁单元模拟，其中拱肋截面选用施工阶段联合截面模拟，扣锚索、揽风索选用等效桁架单元模拟，吊杆选用只受拉桁架单元模拟。主拱包含982个节点，1 866个单元；扣塔系统包含3 969个节点，8 821个单元；主梁包含345个节点，344个单元。扣塔及主桥计算模型如图3所示。

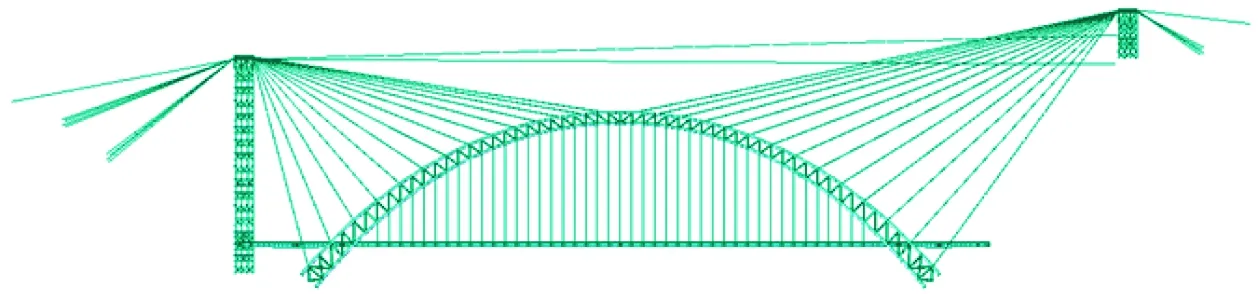
图3 扣塔及主桥计算模型

桥位处地貌属于堆积高山峡谷区，两岸地面高程差较大，因此两侧扣塔高度悬殊，西侧上下游塔架基础位置相差21 m；东侧上下游基础相差20 m。为防止扣塔失稳，在西侧扣塔顶设置纵向揽风索约束扣塔顺桥向变形，在空钢管合龙后拆除塔架和扣锚索，之后灌注混凝土至拱肋。

3 缆索支架系统变形与受力有限元计算分析结果

3.1 缆索施工支架位移结果分析

拱肋吊装过程中，缆索系统在吊塔顶部横移来吊装不同节段拱肋，缆索滑移及其几何非线性必然对塔架产生更不利的影响，因此需验证吊装各节段时施工塔架上部的吊塔变形，依据文献[12]，塔脚约束为铰接时塔顶位移不得超过H/150～H/200(H为吊塔高)。则吊塔塔顶的纵向位移应不大于143 mm。塔脚约束为固结时塔顶位移不得大于H/400～H/600，则西侧扣塔顺桥向最大变形应不超过32 cm；东侧最大变形不超过4.1 cm。

限于篇幅，分别提取吊重2号、4号、6号、9号、11号、14号节段时的吊塔结果，缆索的滑移及索塔的一体化将会加剧塔架的变形，在最不利纵向风载作用下，吊重2号节段时，吊塔顶纵向位移达到最大183 mm，超出了规定限值。由图4可知，无风载作用下，吊重2号节段于西侧时，塔顶纵向位移达到最大，为102 mm，小于规程要求。因此建议在无风或风载较小时吊装拱肋。

图4 无风载时吊装不同节段时吊塔

将缆索系统吊装各节段拱肋时得到的吊塔最大支反力，作为吊塔传递荷载作用于扣塔，则因缆索非线性及滑移产生的影响也将反映至扣塔。考察拱肋吊装过程中扣、锚索及揽风索对扣塔的影响，计算得到扣塔变形结果。西侧扣塔位移在施工至14号拱肋节段时达到最大，为向边跨26.9 cm，东侧扣塔在施工9号拱肋节段时纵向位移达到最大，为向中跨方向1.8 cm。扣塔顺桥向位移均小于规定限值。

3.2 缆索施工支架应力结果分析

考虑吊塔在自重、缆索系统及纵、横向风载作用下受到的最大压应力，当考虑缆索的几何非线性及滑移时，缆索内力较大使得传递至吊塔的作用力相应增大，将导致塔架应力结果有所增加。由图5可知：(1)跑车越靠近边跨侧，吊塔受力越不利。(2)同等吊装重力时吊装节段越靠近跨中，吊塔受力越不利。由于吊装重力悬殊，吊装2 500 kN重的9号节段时，压应力值达到最大186.75 MPa，未超过Q235钢材强度设计值205 MPa。因此吊塔的应力结果是符合要求的。

图5 吊塔立柱组合压应力

通过计算分析比较，在由西至东方向风载作用下，扣塔受力最不利，吊塔传递荷载作为外荷载作用至扣塔，则因缆索非线性及滑移产生的影响也将反映至扣塔。西侧扣塔在吊装14号节段时，空钢管立柱应力达到最大为185 MPa；东侧扣塔在吊装9号节段时，钢管立柱应力达到最大，为110 MPa，其应力值均小于钢材Q235容许应力值187 MPa。但西侧上下游塔架横联杆件应力较大，主要由于上下游塔架存在一定高差，风载及扣锚索对上下游塔架作用力不平衡造成，在施工过程中需重点监测。

3.3 施工支架对主拱线形的影响

施工塔架顺桥向位移对主拱线形将产生一定影响，但通常计算分析往往不建塔架模型，即按照扣索上部节点位移为零处理，这和实际是不相符的。本文比较了考虑扣塔和不考虑扣塔两种情况下拱肋竖向累计位移的差异，提取空钢管拱合龙后各节段竖向累计位移，由图6可知，考虑扣塔时，扣塔偏位对左半跨中部范围内拱肋的竖向位移影响较大，对右半跨拱肋的竖向位移影响较小，因此，当塔架较高或塔顶变形较大时，在设计及计算时需考虑塔架对拱肋线形的影响[13-14]。

图6 钢管合龙后拱肋竖向位移对比图

4 缆索支架系统变形与受力的解析计算分析结果

根据文献[5]理论公式计算主索内力，这是目前施工单位通常采用的计算方法，不考虑主索在鞍座的滑移，且不计施工塔架偏位影响，主索的内力、垂度和塔底反力的计算都不够精确，这也导致施工塔架的受力与变形结果有一定偏差。

桥位处多年昼夜温差约20℃，需考虑温度对主索受力的影响。分别计算吊装2 500 kN及1 500 kN节段于西侧50 m、跨中、东侧50 m时主索水平张力，水平张力方程如下

(1)

按照索鞍两侧主索内力相同原则，可由主索水平张力推算出主索垂度及竖向力。对施工塔架施加解析法计算出的主索水平力及竖向力，即可计算出塔架的变形与受力情况。由于解析法计算的施工塔架部分变形与受力结果均未超出规定限值，且与有限元结果相近，详细的解析结果与有限元结果的对比分析均在第5部分给出。

5 有限元与解析法的对比

列表对比分析两种方法考虑风载作用下的计算结果，对于主索内力的计算结果如表1所示，索力解析计算值均比有限元计算值小，差距在8%以内，吊重于跨中时两者索力值更为接近，吊重越向支点侧差距越大，说明考虑主索滑移及施工塔架偏位时索力的计算值偏大，索力增大必然对施工塔架受力与变形产生不利影响，对于施工塔架吊塔顺桥向位移的结果比较，如表2所示，两者差距在10%以内，且有限元计算结果偏大； 对于吊塔应力的比较，如表3所示，两者差距在8%以内，且有限元计算结果偏大；这是由于有限元模拟计算出的索力值较大以及索塔一体化带来的影响。由两种方法计算的各项结果差距均小于10%，由此证明本文有限元模拟方式能够对缆索吊装施工过程进行精确模拟并指导施工，其结果是可靠并且偏于安全的。

表1 主索内力解析法与有限元法比较

表2 吊塔顶顺桥向位移解析法与有限元法比较

表3 吊塔应力解析法与有限元法比较

6 结论

针对430 m大跨径拱桥施工缆索支架体系的有限元模型的非线性计算分析，并与理论公式对比分析，得到结论如下。

(1)有限元方法及解析法计算的主索内力、塔架变形及应力结果差距在10%以内，且有限元方法计算结果均偏大，说明建立的模型考虑了主索非线性及滑移的吊塔及主索一体化，能够较精确地模拟实际情况。有限元方法计算结果偏大，也说明计入主索非线性、滑移及塔架偏位对缆索吊施工体系产生了不利影响。

(2)通过对缆索吊施工过程进行有限元计算分析，发现顺桥向风载对施工塔架变形及受力都产生了较大影响，甚至导致变形增大至超出塔架偏位限值，无法满足塔架施工的安全要求，因此需在无风或风载较小时吊装拱肋。

(3)考虑施工塔架的建模方式更贴近实际状态，通过比较是否考虑施工塔架时拱肋施工阶段的线形差异，认为当扣塔较高或塔顶变形较大时，拱肋线形的确定需要包含对扣塔的建模分析。

[1] 罗亭.拱桥缆索吊装施工索力简化计算方法[J].公路工程，2016(3)：122-124，140.

[2] 赵人达，张正阳.我国钢管混凝土劲性骨架拱桥发展综述[J].桥梁建设，2016(6)：45-50.

[3] 陈小波.大跨径钢管混凝土劲性骨架拱肋施工阶段受力与稳定分析[J].中外公路，2015(1)：134-138.

[4] 陈强，王树国，彭学理，等.宜万铁路落步溪大桥提篮型拱肋钢管骨架吊装方案计算[J].铁道标准设计，2010(8):178-182.

[5] 周永兴，何兆红，邹毅松，等.路桥施工计算手册[M].北京：人民交通出版社，2001.278.

[6] 陈俊松，刘飞.缆索吊装系统主索的受力与变形计算[J].五邑大学学报(自然科学版)，2014(4)：37-42.

[7] 郭常瑞，卞佳.悬索桥加劲梁吊装过程的缆索系统计算分析[J].中外公路，2014(5)：186-191.

[8] 张二华，黄珍.大跨径劲性骨架钢管拱桥拱肋施工过程仿真分析[J].重庆交通大学学报(自然科学版)，2013(S1)：852-855.

[9] 曾勇，谭红梅.基于塔-索-拱建模的大跨钢管混凝土拱桥施工阶段动力特性研究[J].重庆交通大学学报(自然科学版)，2014(5)：17-21，36.

[10] 李哲，赵东升，颜东煌，等.大跨度钢管混凝土拱桥制造线形计算方法研究[J].中外公路，2015(4)：107-110.

[11] 赵朝阳，杨文爽，李传习，等.缆索吊装主索系统的受力分析算法与工作性能[J].广西大学学报(自然科学版)，2010(4)：615-620.

[12] 中华人民共和国住房和建设部.JGJ 145—2013 混凝土结构后锚固技术规程[S].北京：中国建筑工业出版社，2013.

[13] 邓江明.缆索吊装扣塔偏位对拱肋高程影响的几何分析[J].重庆交通大学学报(自然科学版)，2009(3)：505-507.

[14] 梅盖伟.拱桥缆索吊装扣塔偏位对拱肋节段安装的影响[J].重庆建筑，2015(7)：34-37.