中国制造业增加值ARMA分析
殷英 谭元发


摘要:自改革开放以来,中国制造业有了显著的发展,无论制造业总量还是制造业技术水平都有很大的提高,制造业的增加值基本稳定在当年GDP的30%以上。本文运用计量经济学原理对我国1966年以来制造业增加值进行动态分析,建立ARMA模型,并利用历史数据论证模型的正确性,研究制造业增加值变化趋势和特征,给出了制造业增加值的预测方法,为经济决策提供依据。
Abstract: Since the economic reform and opening, China's manufacturing industry has a significant development, both total economic output and manufacturing technology level has greatly improved, manufacturing output basically stable at more than 30% of GDP. This paper analyses the manufacturing value added in China with the theory of econometrics since 1966, establishes ARMA analyzing model,checks the correctness of this model by using history-data, discusses the trend and character of the variety of the manufacturing value added in China and presents forecast of the manufacturing value added,and provides the basis for economic decisions.
關键词:制造业增加值;时间序列;ARMA模型
Key words: manufacturing value added;times series;ARMA model
中图分类号:F403 文献标识码:A 文章编号:1006-4311(2018)36-0108-03
0 引言
自改革开放以来,中国制造业有了显著的发展,无论制造业总量还是制造业技术水平都有很大的提高,制造业的增加值基本稳定在当年GDP的30%以上。同时,国家财政收入的50%来自制造业。2015年国家制定“中国制造2025”,制造业供给侧结构性改革取得新突破,通过“积极稳妥化解过剩产能、促进工业企业降本增效、补齐实物产品质量短板等方面的突破”,制造业将逐步实现由“中国制造”到“中国智造”。本文运用计量经济学理论建立中国制造业增加值的时间序列模型,分析制造业增加值内在关系和变化趋势.并运用所建模型对制造业增加值进行预测,为政府选择预测经济发展的统计模型提供参考。
1 制造业工业增加值数据分析与处理
本文根据《中国统计年鉴,2017》和《世界银行》等收集了1966~2017年的制造业增加值有关数据,为了方便用MVAt表示制造业增加值.
图1为1966~2017年制造业增加值变化曲线,从图1可以看出MVAt是一个非平稳序列,它的变化呈指数变化趋势。
对MVAt作对数变换后进行逐期差分运算,用LNMVAt表示。
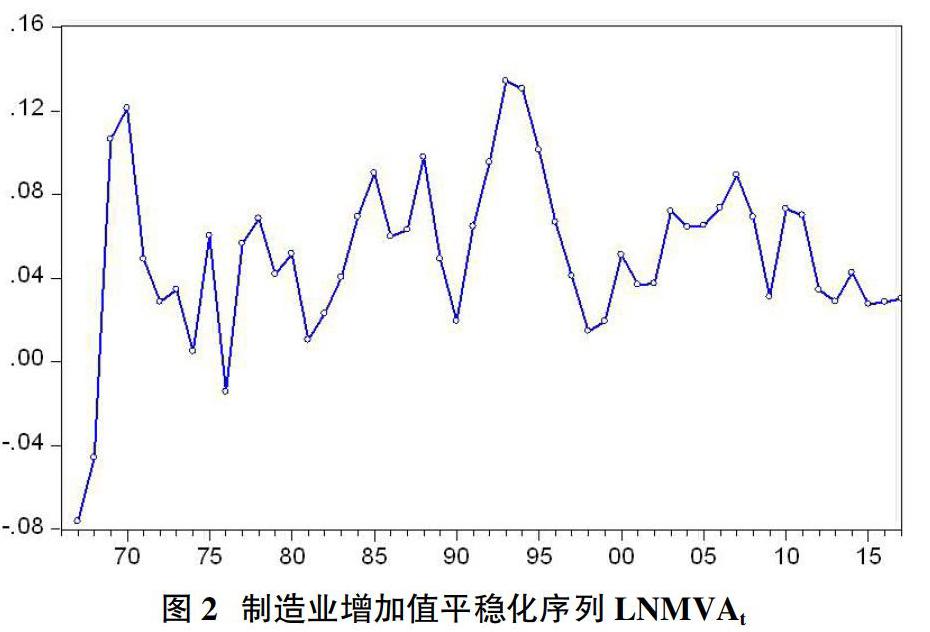
得出时间序列LNMVAt的变化趋势如图2所示。
从图2可看出,一阶差分后的时间序列变得较为平稳,应用Eviews8.0软件对LNMVAt进行ADF平稳性检验,检验结果由表1可见,由于ADF统计值为-5.0123小于在1%的显著水平-3.5744,时间序列LNMVAt拒绝单位根假设,LNMVAt在1%显著水平上是平稳的。
2 ARMA模型拟合
序列LNMVAt的自相关(AC: Autocorrelation)图和偏自相关(PAC: Partial Correlation)图如表2,自相关函数AC和偏自相关函数PAC具有拖尾且依正弦趋近于零的特性。根据Boy-Jenkins模型识别方法,用ARMA(p,q)模型进行拟合。由表2可以看出,自相关函数AC到滞后1阶呈正弦衰减,都在95%置信区间内,偏自相关系数PAC在滞后1阶、2阶、7阶处显示出统计上的尖柱,其余在95%置信区间内。因此可以考虑p=2,q=0或1建立ARMA(p,q)模型:Φp(B)LMVAt=Θq(B)ut
其中Φp(B)和Θq(B)分别表示B的p,q阶多项式,分别称为自回归算子和移动平均算子,B表示滞后算子,B LNMVAt=LNMVAt-1,ut表示白噪声。
用Eviews8.0软件进行拟合,根据上述分析,建立ARMA(2,0)、ARMA(2,1)时间序列模型,如表3、4所示。
从表5的比较,选择模型ARMA(2,0),模型ARMA(2,0)的估计方程为:
(10.3) (3.5) (-2.19)
各系数t-检验显著,表3中最下方给出的是滞后多项式Φ(MVA-1)=0的倒数根,这些根在单位圆内时,过程ARARMA(2,0)是平稳的。
3 模型的检验
H0:et相互独立(et为残差序列)。
设m是最大滞后期,根据实际情况,取m =12,检验统计量
rk(e)是残差序列自相关函数,用Eviews8.0软件进行计算,得出模型ARMA(2,0)的Q-统计量相伴概率,如表6所示。
Q-檢验的相伴概率远大于检验水平0.05,因此不能拒绝原假设,即可以认为模型ARMA(2,0)估计结果的残差序列不存在自相关。
4 利用模型进行预测
根据上述分析,利用ARMA(2,0)运用EViews8.0软件计算2016年和2017年的制造业增加值,并对2018年制造业增加值进行预测,结果见表7。
从表7可知,用ARMA(2,0)模型对制造业增加值进行预测,2016与2017年预测值与实际值误差分别为2.6%和1.5%,2018年制造业增加值增长速度预计为6.8%,这与预期经济增长速度相近。
5 结语
建立经济预测模型的方法较多,运用时间序列建立经济模型具有一定准确性.本文建立的ARMA模型对中国制造业增加值进行预测,其误差不超过3.6%,其精度满足通常标准,并对2018年制造业增加值进行预测,其增长速度为8.3%,“十二五”期间,我国制造业实现了年均增速为9.81%,2016年的增长速度为6.8%,2017年的增长速度为6.1%,与发展目标相符合,说明模型是可行的。
参考文献:
[1]樊欢欢,李嫣怡,陈胜可.EViews统计分析与应用计量经济学[M].北京:机械工业出版社,2011-07.
[2]殷英,谭元发.我国新能源ARMA模型分析与预测[J].数学理论与应用,2009-04.
[3]谭元发.能源消费与工业经济增长的协整与ECM分析[J].统计与决策,2011-04.
[4]Jeffrey M. Woddridge, Introductory Econometrics: A Modern Approach. Third Edition[M]. Beijing: Tsinghua University Press,2007.
[5]Johansen, S. Statistical analysis of cointegration vectors [J]. Journal of Economic Dynamics and Control, 1988-12:231-254.

