3种模型在GF-2影像的生物量估测中的比较

徐梦伶，林 辉，孙 华，严恩萍，周普良

（林业遥感大数据与生态安全湖南省重点实验室，湖南 长沙 410004）

生物量是指某一时间单位面积或体积栖息地内所含一个或一个以上生物种，或所含一个生物群落中所有生物种的总个数或总干质量（包括生物体内所存食物的质量）。在森林生态系统中，森林的生物量是评价森林生态系统碳循环的重要载体及指标参数[1]。用传统的生物量研究方法获取推算生物量所需的实测数据的一般方法都是在取样区进行每木调查、树干解析、全伐小样方里的灌木与草本等。这种操作方法不仅需要耗费大量的人力资源和时间，而且会对取样区的生态环境造成不同程度的破坏。并且由于样地数量有限，很难批量获取区域森林结构信息[2,3]。现今广泛应用遥感(RS)、地理信息系统(GIS)和全球卫星定位系统(GPS)等3S技术结合的手段，调查区域森林生物量。目前有较多的遥感估测生物量研究，但大多数基于中低分辨率。随着高分系列影像数据的出现，高空间分辨率数据的研究也在开展之中。当前研究基于线性模型和非线性模型的生物量估测也要较多研究，其中曾晶等[4]利用高分一号遥感影像，建立生物量的多元线性模型，反演精度为80. 75 %；孙雪莲等[5]运用随机森林方法结合遥感因子研究思茅松人工林生物量，估测出人工林单位面积生物量为59. 09 t/hm2，总生物量为3.644×106t。目前，生物量神经网络模型很多，如线性网络、回归网络、后向神经网络、感知器神经网络及径向基函数神经网络等[6-7]。实验表明，在生物量估测与实测数据计算中，人工神经网络法估测相对误差较小，约小于15%。引入坡度、坡向、海拔和立地类型作为神经网络模型的自变量，有益于提高生物量的估算精度[8]。估算区域生物量还可以通过数学方法建模实现，不同的森林类型和树种类型，所建立的数学模型不尽相同[9-11]。

通过归纳现有的经验模型研究结果来看，生物量估测模型大多采用线性或者非线性模型。同时，关于高分二号影像建立模型估测生物量的研究较少。本研究为探索基于高分二号影像的光谱信息估测生物量的模型效果，以黄丰桥林场为研究区，依据实测的样地生物量为因变量，提取高分二号影像的光谱信息，结合植被指数以及坡度、坡向、海拔等因子为自变量，通过提取自变量主成分，建立主成分回归模型，还建立了偏最小二乘回归模型和BP神经网络模型，对模型进行精度验证以及预测性检验对比。

1 研究区概况

研究区黄丰桥林场位于湖南攸县东北部，罗霄山脉中段，酒埠江风景区内。现有林地总面积10 122.6 hm2，森林覆盖率为86. 24%。全场地貌以中低山为主，境内最高海拔1 270 m，最低海拔115 m，坡度介于20°～35°之间。林场地处中亚热带季风湿润气候区，年均气温17.80 ℃；平均无霜期为292 d；年均降水量1 410. 8 mm（见图1）。

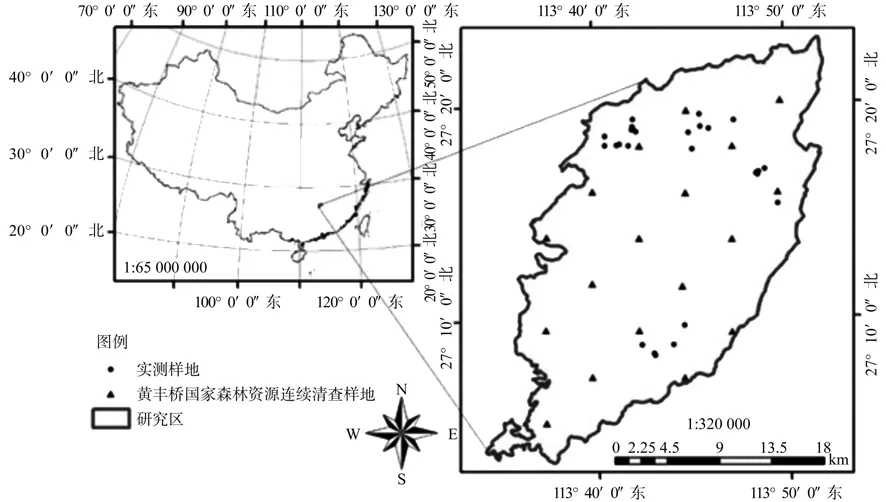
图 1 研究区位置及样地分布Fig.1 Location of the study area and plots

2 材料与方法

2.1 野外数据收集与处理

样地数据包括两个部分：第一部分是在攸县黄丰桥林场内设置了29个30 m×30 m的样地，采用RTK和全站仪确定样地中心点及样地内各单木的位置，在样地内对每株树木进行树种、树高和胸径调查；第二部分数据来自2014年国家森林资源连续清查样地，落在研究区范围内有18个样地。共47个样地，分布情况如图1所示。

根据样地每木检尺数据，对样地内的所有乔木进行生物量计算，生物量计算采用2010年李海奎在《中国森林植被生物量和碳储量评估》中的回归模型[12]，样地生物量计算结果见表1。随机选取34个实测样地生物量参与建模，剩余13个样地生物量用于模型验证。

2.2 GF-2数据预处理

研究以2015年11月5日接收的高分二号（GF-2）卫星数据为数据源，该数据包括6景分辨率4 m的多光谱数据和6景分辨率1 m的全色波段数据。

在ENVI5.1 软件中，对GF-2原始影像的多光谱影像和全色影像进行辐射定标和FLAASH大气校正，去除了大气对影像的影响，植物的波谱曲线更加接近真实的植物波谱曲线，图像质量得到明显提高。采用Gram-Schmidt方法进行融合，融合后的影像既具有全色影像的1 m分辨率，同时又具有多光谱特征。在研究区内使用RTK在交叉路口上采集21个控制点，利用控制点坐标对影像进行几何精校正。将融合精校正之后的6景影像进行镶嵌和裁剪，得到研究区影像图。

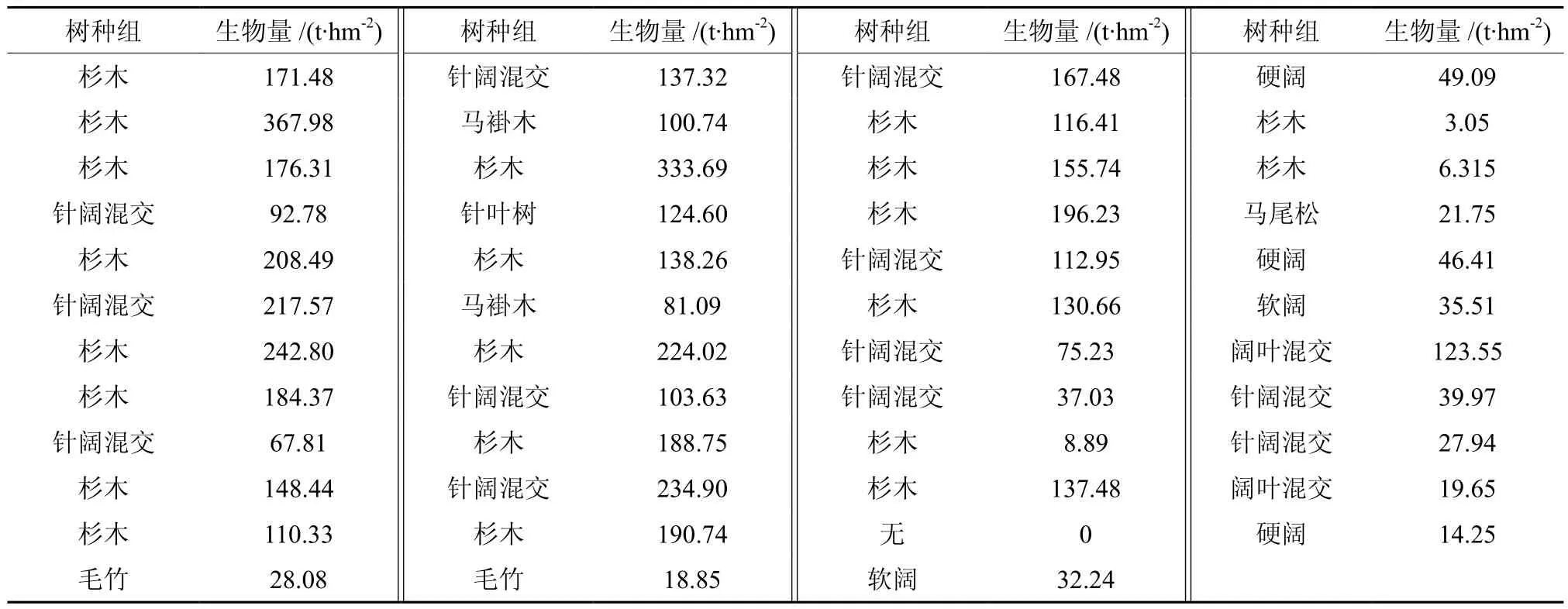
表1 样地生物量计算结果Table 1 Sample biomass calculation results

2.3 GF-2建模因子的提取

2.3.1 光谱因子

以样地实测坐标为准，选取GF-2影像4个波段的灰度值，波段灰度值倒数作为生物量估测的建模因子，即B1、B2、B3、B4、1/B1、1/B2、1/B3、1/B4。

同时相关研究表明，不同的光谱通道经线性或非线性组合构成的指数，对植被长势和分布情况具有一定的指示意义[13-14]。

2个 波 段 的 比 值：B12=B1/B2、B13=B1/B3、B14=B1/B4、B23=B2/B3、B24=B2/B4、B34=B3/B4。

3个波段组合：B123=(B1+B2)/B3、B124=(B1+B2)/B4、B132=(B3+B1)/B2、B134=(B1+B3)/B4、B142=(B1+B4)/B2、B143=(B1+B4)/B3、B231=(B2+B3)/B1、B234=(B2+B3)/B4、B241=(B2+B4)/B1、B243=(B4+B2)/B3、B341=(B3+B4)/B1、B342=(B3+B4)/B2。

4个 波 段 组 合：B1234=(B1+B2)/(B3+B4)、B1324=(B1+B3)/(B2+B4)、B1423=(B1+B4)/(B3+B2)、B2314=(B3+B2)/(B1+B4)、B123-4=(B1+B2+B3)/B4、B234-1= (B2+B3+B4)/B1。

2.3.2 植被指数

根据相关研究[15-18]，提取归一化植被指数（NDVI）、比值植被指数（RVI）、土壤修正植被指数（SAVI）和大气阻抗植被指数（ARVI）作为建模因子。

2.3.3 地理因子

在ArcGIS中，依据研究区的DEM数据，提取样地坡度、坡向、海拔因子。

2.3 肥水管理 第1年，从5月底开始，当年枝条长到10 cm左右时，20天追施1次尿素，每次100 g/株，连施2～3次。9月底10月初每亩施入腐熟有机肥2～3 m3，复合肥50 kg。

3 结果与分析

3.1 模型的构建

3.1.1 主成分回归模型

主成分分析方法是把原来多个变量划为几个少数综合指标的统计分析方法，就是一个降维处理。在SPSS 20. 0中，利用降维因子分析模块进行主成分分析，按累积方差贡献率85%的准则，建立了前3个主成分，结果如表2所示。

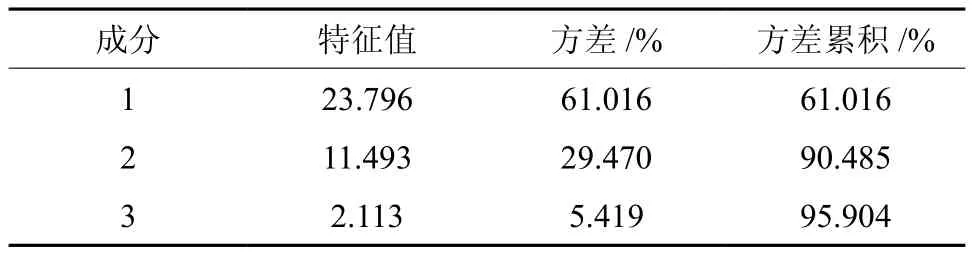
表2 主成分特征值及方差解释Table 2 Principal component eigenvalues and variance interpretation

由表2可知，取到前两个时，样本方差累积贡献率达到90.485%，大于 85%，己涵盖了原始变量的主要信息，符合主成分提取要求。同时特征值作为某种程度上主成分影响力度大小指标，主成分个数提取原则为主成分对应特征值大于1的前m个主成分。因此以生物量作因变量，前3个主成分累积的贡献率为95.904%，考虑取前3个主成分进行生物量估测，代替原始变量，保存前3个主成分因子作为自变量构建模型。

采用SPSS软件进行多元线性拟合，得到回归模型为：

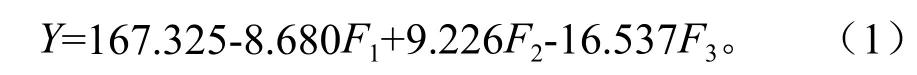
式中：Y为生物量；F1为第一主成分；F2为第二主成分；F3为的第三主成分。

模型经方差分析，F值为3.351，Sig.=0.039，Sig.值小于0.05，表明了因变量和自变量之间线性关系显著；决定系数R2为0. 443，拟合情况良好。

3.1.2 偏最小二乘回归模型

偏最小二乘回归采用对变量X和Y都进行分解的方法，使用偏最小二乘回归分析方法的变量投影重要性指标（VIP）、变量解释能力来决定选择几个变量参与建模。其中，图2列出了各变量的VIP值。

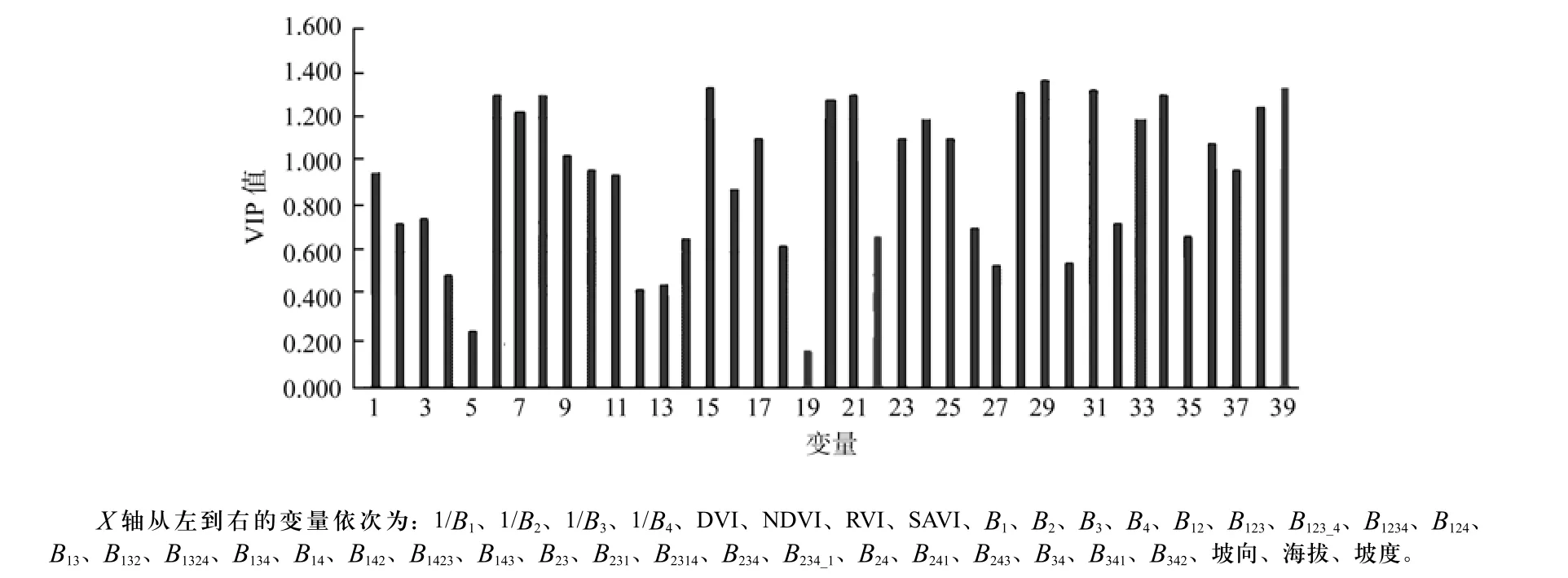
图2 变量投影重要性指标直方图Fig.2 Variable projection importance indicator histogram

变量投影重要性指标即自变量Xj对因变量集合Y的解释能力。通常若自变量Xj对应的VlPj＞1，则Xj解释Y时具有重要的作用。因此，如图2所示，在整个回归分析过程中有20个因子的变量投影重要性指标小于1而被剔除。对剩余19个因子进行回归建模，其中偏最小二乘回归分析结果见表3。

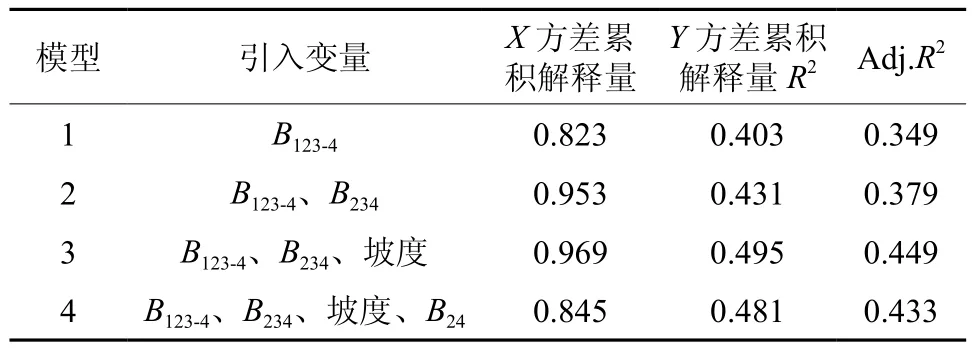
表3 偏最小二乘回归分析结果Table 3 Partial least squares regression analysis results

从表3可知，在潜在因子个数达到4个以后，自变量的累积解释量和因变量的累积解释量的增幅开始减少，最终得到3个偏最小回归模型：

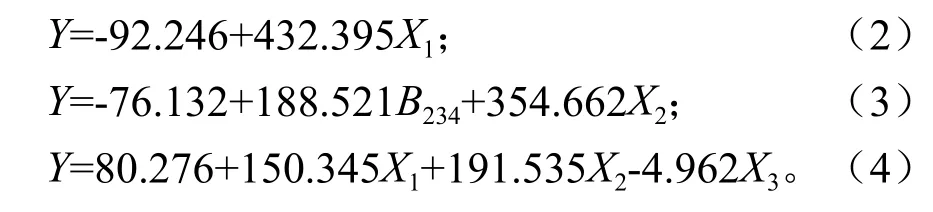
式中：Y为生物量；X1为B123-4；X2为B234；X3为坡度。

根据决定系数R2值，可知，当引入变量数为3个时，R2值最高。因此，式（2）和式（3）舍去，保留式（4）为偏最小二乘回归模型。

3.1.3 BP神经网络模型

本文基于MATLAB2014a软件构建生物量的BP神经网络模型，其建模因子与实测样地的生物量进行相关性分析，得到结果见表4。

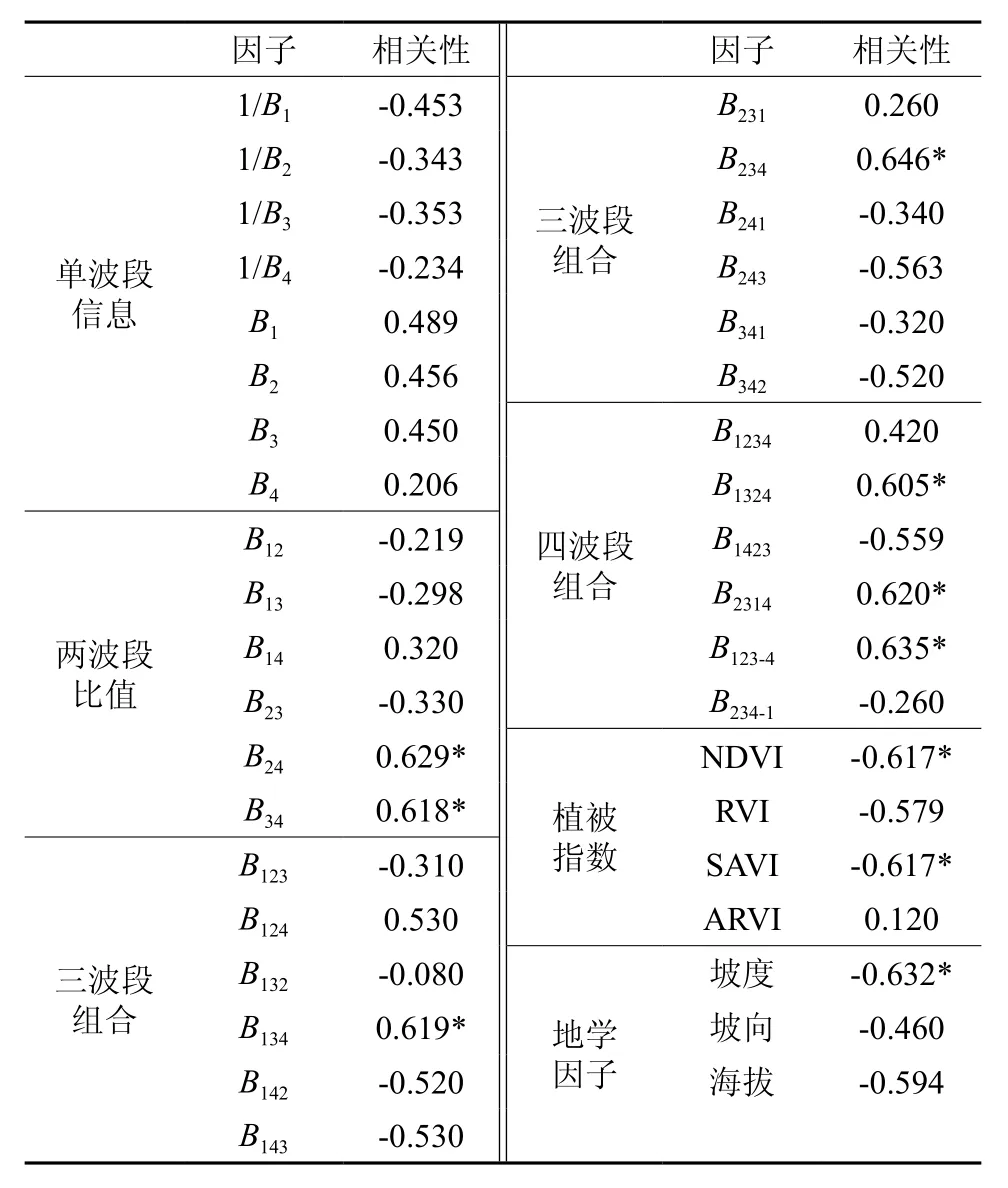
表4 生物量与各个因子的相关系数†Table 4 Correlation coefficient of biomass with each factor

选取相关性较高的10个因子作为输入层因子， 即B234、B123-4、B24、 坡 度、B2314、B134、B34、SAVI、NDVI、B1324。以样地的生物量作为输出层变量，设置隐含层的节点数为9，构建一个多输入单输出的三层网络结构，通过多次反复训练和样本精度的测验，构建生物量估测BP神经网络模型。

通过该网络模型的输出，仿真结果的相关系数达到0.801 4，平均相对误差为15.3%，最大相对误差不超过24.3 %，达到较好的预测标准。

3.2 模型精度检验

根据建立的主成分回归模型、偏最小二乘回归模型和BP神经网络模型结果来看，3种模型都取得了较好的拟合结果，为了进一步判定哪个模型的拟合效果最佳，本论文对3个模型做了精度检验。根据3种方法所建模型来算出13个样地的生物量估测值，通过实测值和估测值的拟合效果的决定系数（R2）和所建模型的残差，来检验模型预测值和实际观测值是否存在较好的拟合效果，以及残差是否落在置信带，并计算它们的均方根误差(RMSE)和估测精度(EA)作为模型预测性能的评价指标[19]，结果如图3所示。将3种方法建立的模型检验结果汇总，结果见表5。

图3 3种生物量反演模型精度评价Fig.3 Three biomass inversion model accuracy evaluation

表5 3种生物量反演模型精度验证比较Table 5 Comparison of three biomass inversion model accuracy verification

由图3可知， 主成分回归模型的实测值和预测值的决定系数R2为0.44；偏最小二乘回归模型的R2为0.50；BP神经网络模型的R2为0.79。偏最小二乘回归的残差散点图上显示预测值与实测值虽然有较好的拟合关系，但残差趋向置信带一边，随机性较差。BP神经网络模型残差图散点分布比较均匀，说明拟合效果好。

由表5可知，主成分回归模型的估测精度为65.83%，均方根误差为57.17；偏最小二乘回归模型的估测精度为67.66%，均方根误差为54.11；BP神经网络估测精度为78.62%，均方根误差为35.77。

4 结 论

研究以攸县黄丰桥林场为研究区，通过对GF-2影像进行预处理，结合实测样地生物量值，采用主成分分析、偏最小二乘回归以及BP神经网络3种方法分别建立生物量模型，并进行了精度检验，得到以下结论：

（1）在对GF-2信息提取的过程中，充分利用了影像所带有的信息。本次研究使用了8个单波段信息、24个多波段组合信息、4个植被指数、3个地形因子参与建模，并取得了良好的拟合效果，说明利用影像信息建立生物量估测模型是可行的。

（2）主成分回归模型的实测值和预测值的决定系数R2为0.44，模型的估测精度为65.83%；偏最小二乘回归模型的R2为0.50，模型的估测精度为67.66%；BP神经网络模型的R2为0.79，模型的估测精度为78.62%。比较可知，研究构建BP神经网络模型效果最好。

GF-2卫星是国产的高分辨率卫星，在生物量估测方面表现出了巨大的应用潜力，但利用GF-2影像进行生物量估测的研究较少，研究通过对3种模型的精度比较，为基于GF-2影像的攸县黄丰桥林场的生物量估测提供参考。BP神经网络可用于实测数据积累较多的生物量估测研究，在后期逐步增加实测生物量数据的基础上，有望进一步提高不同模型在影像上的生物量估测精度。与同类研究相比，研究所选建模因子多为光谱信息因子，对于其他因子，例如不同窗口的纹理特征等能否有效提高模型的精度，有待进一步研究。

[1]Brown S, Sathaye J, Cannell M,et al. Mitigation of carbon emissions to the atmosphere by forest management[J].Commonwealth Forestry Review, 1996 , 75 (1):4745-4755.

[2]王 敏, 李贵才, 仲国庆,等. 区域尺度上森林生态系统碳储量的估算方法分析[J]. 林业资源管理, 2010(2):107-112.

[3]Christina Eisfelder, Claudia Kuenzer, Stefan Dech. Derivation of biomass information for semi-arid areas using remote-sensing data[J]. International Journal of Remote Sensing, 2012, 33(9):2937-2984.

[4]曾 晶, 张晓丽. 高分一号遥感影像下崂山林场林分生物量反演估算研究[J]. 中南林业科技大学学报, 2016, 36(1):46-51.

[5]孙雪莲, 舒清态, 欧光龙,等. 基于随机森林回归模型的思茅松人工林生物量遥感估测[J]. 林业资源管理, 2015(1):71-76.

[6]王立海, 邢艳秋, WANGLi-hai,等. 基于人工神经网络的天然林生物量遥感估测[J]. 应用生态学报, 2008, 19(2):261-266.

[7]金亚秋, 刘长龙. 人工神经网络模型反演植被生物量参数[J].遥感学报, 1997, 1(2):83-87.

[8]胡上序, 程翼宇. 人工神经元计算导论[M]. 北京:科学出版社, 1994.

[9]李粉玲, 李京忠, 张琦翔. DEM提取坡度•坡向算法的对比研究[J]. 安徽农业科学, 2008, 36(17):7355-7357.

[10]Houghton R A, Lawrence K T, Hackler J L,et al.The spatial distribution of forest biomass in the Brazilian Amazon: a comparison of estimates[J]. Global Change Biology, 2001,7(7):731-746.

[11]Haripriya G S. Estimates of biomass in Indian forests[J]. Biomass& Bioenergy, 2000, 19(4):245-258.

[12]李海奎. 中国森林植被生物量和碳储量评估[M]. 北京:中国林业出版社, 2010.

[13]Guangxing Wang, Maozhen Zhang, George Z Gertner,et al.Uncertainties of mapping aboveground forest carbon due to plot locations using national forest inventory plot and remotely sensed data[J]. Scandinavian Journal of Forest Research, 2011,26(4):360-373.

[14]Zhou Y, Zhang Y, Vaze J,et al.Improving runoff estimates using remote sensing vegetation data for bushfire impacted catchments[J]. Agricultural & Forest Meteorology, 2013, s182–183(1):332-341.

[15]Miura T, Huete A, Yoshioka H. An empirical investigation of cross-sensor relationships of NDVI and red/near-infrared reflectance using EO-1 Hyperion data[J]. Remote Sensing of Environment, 2006, 100(2):223-236.

[16]Schlerf M, Atzberger C, Hill J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data[J].Remote Sensing of Environment, 2005, 95(2):177-194.

[17]Hashemi S A, Chai M M F, Bayat S. An analysis of vegetation indices in relation to tree species diversity using by satellite data in the northern forests of Iran[J]. Arabian Journal of Geosciences,2013, 6(9):3363-3369.

[18]Kaufman Y J, Tanré D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS[J]. IEEE Transactions on Geoscience & Remote Sensing, 1992, 30(2):261-270.

[19]孙 华, 鞠洪波, 张怀清,等.三种回归分析方法在Hyperion影像LAI反演中的比较[J]. 生态学报, 2012, 32(24):7781-779.