面向风险均衡的AFDX虚拟链路路径寻优算法
赵长啸,何锋,阎芳,王鹏,*,熊华钢
1.中国民航大学 天津市民用航空器适航与维修重点实验室, 天津 300300 2.北京航空航天大学 电子信息工程学院, 北京 100083
综合化是机载航电系统发展的趋势,综合模块化航电系统(Integrated Modular Avionics,IMA)已成为新一代飞机航电系统的主流应用架构[1],在空客A380、A350,波音B777、B787,中国的C919及处在论证阶段的宽体客机,航电系统都采用了IMA架构。IMA采用综合核心处理系统(Integrated Core Processor,ICP)加载功能软件的方式实现航电功能,并通过航空电子全双工交换式以太网(AFDX)网络实现各系统间信息共享[2]。IMA平台的分区技术[3]和AFDX的虚拟链路(Virtual Link,VL)技术[4]具有系统隔离能力,可以保证驻留于同一平台的航电功能独立的实现其功能。但是目前系统设计中ICP和AFDX网络设计是相互独立的,当将二者进行集成时,ICP中的分区隔离特性有可能被AFDX中VL的不合理规划破坏,产生风险。如一架采用了IMA航电架构的波音787飞机在某次试飞验证实验中,机载总线输出的反推力虚假信号导致了飞机襟翼缩回而飞机被迫紧急终止飞行,此次事故征候的原因是AFDX交换式网络引入了非设计性的系统交互,产生了数据的非预期传输路径,破坏了系统层面的隔离特性,而在系统设计中二者是应该充分隔离的[5-6]。因此在AFDX路径规划中应考虑数据的安全关键特性,保证系统层面的隔离完整性。
目前,对AFDX路径规划问题主要集中在实时性、任务可靠性等方面。文献[7-8]分别采用确定性网络验算和随机网络验算对AFDX网络进行实时性优化;文献[9]提出了一种基于遗传算法的AFDX路径优化方法;文献[10-11]利用轨迹法进行AFDX路径配置,以保证VL的端到端延迟满足系统要求。文献[12-13]则从任务可靠性方面对AFDX网络进行了分析。这些研究分析仅针对AFDX网络本身,未能考虑IMA平台隔离有效性在网络方面的延伸,网络路径规划时未考虑各VL的安全关键程度,有可能造成风险集中,影响整机的安全性。针对AFDX网络的安全性问题,美国联邦航空局发布了专门的咨询通告AC 20-156[14]以指导对AFDX等机载高速互连网络的适航工作。
基于此背景,本文提出了一种面向风险均衡的路径规划(RBPP)算法,给出了民机航电系统功能的风险量化模型;以均衡各物理链路风险和满足系统级隔离需求为目标,并利用仿真实验进行分析对比验证了算法的合理和优越性。
1 IMA平台与AFDX网络集成风险分析
IMA采用的分区技术从时间、空间两方面对共享的平台资源进行了限制,但主要集中于IMA平台,当向网络域延伸时,存在着隔离失效的风险。AFDX网络是IMA采用的网络互连协议,AFDX引入VL对数据流量进行逻辑上的隔离,在每个端系统的输出端,与一条特定的VL相关联的流量用带宽分配间隔(Bandwidth Allocation Gap,BAG)来描述,BAG反映了在同一个VL中两个相邻帧的起始二进制位之间的最小时间间隔[15]。AFDX网络中通信通过VL来实现,但是由于网络中的物理链路可以承载一条或多条VL,这就可能带来不同航电系统间的非预期交互或非设计性交互,即在网络逻辑拓扑中相互隔离的不同VL在物理拓扑中存在互相影响的可能。
本文以一个示例网络对AFDX网络存在的有效隔离不足的风险进行分析。考虑一个由4个交换机(sw1~sw4),9个端系统(es1~es9)的AFDX网络物理拓扑,如图1(a)所示。假设端系统es2和es4可分别实现IMA系统中的不同航电功能,按照安全性评估结果,两端系统间需完全隔离,在IMA高速处理平台端,系统的“健壮分区”特性使得两个端系统满足隔离要求;在网络域,由于AFDX路径规划中未考虑VL承载的信息的安全特性,由端系统es2发出的vl4和由es4发出的vl8,从逻辑拓扑如图1(b)所示,两条VL承载的数据是相互隔离的,但是由于其在实际物理拓扑中共用一条物理链路,因此在端系统es2和es4之间存在着耦合影响关系,破环了全系统的隔离特性。当端系统es2和es4代表影响飞机安全的关键系统时,此问题变得更加严重。如在某型民机航电系统中,完全丧失通信系统或完全丧失导航系统均属Ⅲ类(Major Failure)失效状态,但是同时丧失通信系统和导航系统属于Ⅰ类(Catastrophic Failure)失效状态。因此对于这些关系到飞机飞行安全的系统,系统独立性是安全性分析中需重点关注的问题。
在中国的国产大飞机C919中[16],“航电系统主干网络数据传输采用了ARINC664网络总线,该总线与其他飞机系统的交联非常复杂,与主飞控系统、动力系统、电源系统的部分信号、航电系统部分信号通过ARINC664总线直接交联”。可见,AFDX网络连接了飞控、航电、动力等众多的安全关键系统,不同端系统间的隔离有效性变得尤为重要,因此在对AFDX网络进行VL路径规划时应对风险进行分析考虑。
图1 IMA系统风险示例
Fig.1 Example of IMA system risk
2 系统分析建模
2.1 网络模型
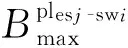
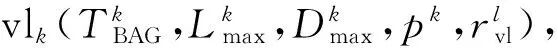
2.2 风险模型
在民机安全性分析中,依据航电系统功能失效对飞机、飞行机组、乘客的影响将失效状态(Failure Condition)划分为5个等级[17]。失效状态等级的确定一般依据已有的相似机型的运行数据、分析数据以及专家经验等信息确定,对于无法通过分析达成共识的失效状态需通过飞行试验确定。同一个航电系统可能有多个失效状态,而不同的失效状态其类别可能不同,一个航电系统的安全关键程度包括两个指标:最高的失效状态类别,高等级失效状态的数量。如某型客机的航电核心处理系统有21个Ⅰ类失效状态,5个Ⅱ类失效状,8个Ⅲ类失效状态;飞机客舱照明系统有2个Ⅲ类失效状态,3个Ⅳ类失效状态,4个Ⅴ类失效状态。可见航电核心系统的安全性关键特性要远高于客舱照明系统。
2.2.1 航电功能失效风险模型
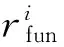
(1)
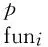
1) 灾难级失效不可容忍策略,即对Ⅰ类失效状态赋值量级远超其他失效状态类别:如取w1=100 000,w2=10,w3=1。对运输类飞机可采用此策略。
2) 不同级别失效风险度差异赋值方式,即赋值体现不同类别风险差异,同时各类别失效状态风险差异是可比拟的,如w1=100,w2=10,w3=1,对通用飞机可采用此策略。
2.2.2 IMA分区失效风险模型
IMA通过分区技术,实现不同航电功能间的逻辑隔离,单一航电功能可以驻留于IMA系统中的一个分区或多个分区,同一分区中不可驻留不同航电功能,因此分区的失效风险与其驻留的航电功能相关,定义分区partitionj的失效风险为驻留于该分区的航电功能的失效风险:
(2)
即当同一航电功能驻留于多个分区时,各分区具有相同的失效风险。
2.2.3 端系统失效风险模型
在AFDX网络中,分区通过端系统进行数据的收发,单一端系统可支持一个或多个分区的通信需求,ARINC 664-P7中给出了端系统和分区的接口[18],如图2所示。VL实现分区到分区的确定性通信,多个分区进行端系统共享时,各分区收发的VL仍能保证确定的独立性,因此端系统esj的失效风险由其支持的分区的失效风险确定,其风险定义为
图2 分区与端系统接口
Fig.2 Interface between partitions and end systems
(3)
在民机中,Ⅰ类失效状态(灾难的)和Ⅱ类失效状态(危险的)的影响范围和后果都是难以接受的,民机系统设计中,失效状态类别每提高一个等级,其相应的可靠性要求提高2个数量级。因此失效风险模型为了体现高安全关键分区对系统安全的影响,定义了RⅠ为当端系统所服务的分区驻留功能包含Ⅰ类失效时的最低风险度;RⅡ为当端系统所服务的分区驻留功能最高为Ⅱ类失效时的最高风险度;RⅢ为当端系统所服务的分区不包含Ⅰ、Ⅱ类失效时的最高失效风险度,且RⅠ>RⅡ>RⅢ。
2.2.4 虚拟链路失效风险模型
在AFDX网络中,端系统之间通过VL进行以太网帧的交换,在计算各VL的风险度由其连接的源和目的端系统确定。
(4)
2.3 VL路径优化模型
对AFDX网络中的VL进行路径规划,是一个带约束的分配问题:
A:VL→PL
(5)
本文提出的RBPP问题以均衡各物理链路所负担的风险,避免风险汇集为目标,同时还需满足系统隔离需求、网络实时性需求以及链路负载等要求。
优化目标为使各物理链路间的风险差异最小,即
(6)
在AFDX网络VL路径规划过程中还有如下约束:
1) 链路负载限制。物理链路承载的所有VL带宽需求之和不应超过物理链路的最大带宽Cj:
(7)
2) 实时性要求。采用文献[19]提出的网络演算方法计算最坏情况下的VL延迟,满足任意VL的最坏情况时延不超过其规定的最大允许时延要求:
(8)
3) 隔离要求。对于具有隔离要求的端系统,优化后的物理路径需满足不同的隔离等级要求:
(9)
(10)
3 基于群粒子算法的RBPP问题求解
RBPP以最短VL路径为基础,以均衡各物理链路间的风险位目标进行优化,同时考虑端系统间的隔离需求及网络中消息的传输实时性要求。AFDX网络VL路径规划为NP问题,采用启发式算法进行问题求解,本文采用粒子群优化(Particle Swarm Optimization, PSO)算法进行求解。
3.1 问题描述
群粒子算法是由Kennedy和Eberhart提出的一种基于population的遗传算法[20],其改进了的局部搜索能力较差的缺点。该算法最初由飞鸟集群活动的规律性启发,利用群体智能建立了一个简化模型。粒子群优化算法中每个优化问题的解都是搜索空间中的一只鸟,称之为“粒子”[21]。所有的粒子都有一个由被优化的函数决定的适应值,每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索[22]。
利用群粒子算法求解,首先需定义群粒子及求解空间。在本问题中,将粒子定义为需进行路径规划的VL集合,粒子的位置表示VL的路径规划结果,假设待规划的网络中有VLNUM条VL,则其解空间为VLNUM×PATHNUM维空间,其中PATHNUM为初始化的有效VL路径数量,解为VLNUM个变长数组集合。
优化问题的适应函数由优化目标和惩罚函数组成,第2.3节式(6)已给出了系统优化目标函数,其惩罚函数由分配约束定义,由式(7)和式(8)可得
(11)
适应函数为
Fit(A)=Q(A)+γPE(A)
(12)
式中:Fit(A)为适应函数;Q(A)为由优化目标函数,由算法的优化目标转化得到;PE(A)为惩罚函数,由约束条件转化得到;γ为惩罚函数的权重值。适应函数值越小,则此解的性能越好。
粒子的速度集合为V={v1,v2,…,vVLnum},vi取值范围为在 (-PATHnum+1,PATHnum-1) 的整数,其代表粒子可以移动的距当前位置的最远距离。算法会生成ρ个粒子,随机的初始化各粒子的初始位置和初始速度,算法通过迭代在解空间中寻找最优解。
在搜寻最优解的过程中,粒子记录两个最优值,Pbest为粒子在搜寻过程中记录的最优值,Gbest为整个粒子群所经历的最优解。粒子位置和速度的更新公式为
Vt+1=ωVt+c1r1(Pbest-Xt)+c2r2(Gbest-Xt)
(13)
Xt+1=Xt+Vt
(14)
式中:X为粒子的位置;V为粒子的速度;ω为惯性权重,表示粒子对前速度继承情况;c1、c2为粒子的认知参数和社会参数,代表了粒子向自身最优Pbest和全局最优Gbest推进的加速权值;r1、r2表示在0~1之间的随机数。
3.2 算法步骤
采用PSO算法求解RBPP问题的具体步骤如下:
步骤1依据各端系统失效状态清单计算端系统风险值、VL风险值及VL的隔离需求等级,计算方法见式(1)~式(4)。
步骤2求解各VL的可行路径集合,构建RBPP问题的解空间。
步骤3对待求解的VL进行粒子编码。
步骤4设置粒子群规模及迭代次数,初始化粒子位置及初始速度。
步骤5依据式(13)~式(14)更新粒子位置及速度,计算适应度函数,并记录局部最优解及全局最优解。
步骤6完成预设更新次数或满足终止条件,对全局最优解进行式(9)的符合性检查,若满足条件,输出结果;否则返回步骤4重新计算。
3.2.1 构建解空间
对于AFDX虚拟链路的路径优化问题,PSO中每一个粒子代表了所有需要优化的VL集合,粒子的位置代表了所有VL从源端系统经过交换机到目的端系统的路径。直接求解所有VL的路径,尤其对于含有多播VL的AFDX网络,算法实现十分困难,因此本算法中首先对各VL求解其可能的路径集合,在此基础上然后构建PSO问题的解空间,求解RBPP下的最优解。
1) 单播VL:对于单播VL,采用Dijkstra最短路径算法[23],针对每条VL进行路径规划,选取较短的前PATHnum条路径构建最终算法的可行解。
2) 多播VL:对于多播VL,采用一般的最小Steiner树算法[24]求解多播VL的最短路径算法,选取树的权值较小的前PATHnum颗树构建最终算法的可行解空间。
PATHnum的数值可依据不同的网络进行确定,对于一个具有VLnum条VL的AFDX网络,RBPP问题的解空间为VLnum×PATHnum维空间。
3.2.2 解空间编码
由于每条VL所经过的交换机数目不定,因此各vl的路径采用变长编码方式。
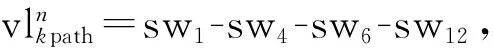
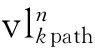
以树形结构进行存储和操作。
3.2.3 设置参数
在文献[25] 中的PSO推荐参数值为ω=0.9,c1=c2=2。群粒子规模设置为20,迭代最大次数为2 000,各粒子位置及初始速度随机设置。
3.2.4 隔离有效性检验
对求得的最优解依据式(9)进行隔离有效性的检验,所有VL的隔离有效性满足,则结果为当前AFDX网络的VL路径规划结果。否则将当前位置以(Path,k)的格式记录于invalid集合,其中Path为当前粒子位置,即VL路径规划结果,k为不满足的隔离条件数量。返回步骤4重新开始计算。
3.2.5 粒子更新及终止条件
粒子位置、速度依据式(13)和式(14)更新,对更新后的粒子位置,进行有效性检查,若当前位置属于invalid集合,则跳过适应度函数计算,并更新粒子位置及速度。
若当粒子位置更新10次,全局最优解Gbest不再变化或粒子位置更新达到2 000次时,则终止更新,当前的全局最优位置,即为问题的解。
当invalid集合中元素个数达到20时,即表示PSO算法整体执行了20次,找到了20个符合风险均衡但不满足隔离需求的路径规划方案。此时表示,网络可能不存在满足所有隔离需求的配置方案,此时从这20个方案找出与隔离方案要求最接近的方案作为次优解,并给出不满足的隔离需求供系统设计者进行VL的重新优化。
4 实例分析
利用C++构建AFDX网络模型[26],实现AFDX网络协议仿真在此基础上对VL路径规划问题进行分析,实现RBPP算法。仿真运行的硬件系统配置为:Intel i7-2600处理器(主频3.40 GH),内存8 G(1 333 MHz),操作系统 Windows 10(版本号10586)。实验采用的AFDX网络拓扑为文献[27]提出的经典结构如图3所示,以及空客A380采用的AFDX网络结构[28]如图4所示。
图3 典型的工业AFDX网络
Fig.3 Typical industry AFDX network
图4 A380中AFDX网络
Fig.4 AFDX network of A380
4.1 AFDX模型有效性分析
本文采用文献[26]中提出的AFDX仿真平台基础,在文献[9]改进的AFDX仿真平台上进行试验,此仿真平台的仿真模型的精确度在文献[9]中给出了说明。
4.2 实验1
在实际的AFDX网络研发过程中,某些研发单位会将多播VL简化为多条单播VL进行优化配置,以简化优化过程,如在文献[9]中的VL路径规划中将多播VL处理为多条单播VL并以sub-vl进行标记。此处理在多播VL数据流量不大的情况下进行流量均衡算法,对路径规划的结果影响不大,但是对于针对网络风险进行路径规划时,会产生“虚”风险问题,本节以图1、图3、图4所示的交换机网络为例进行分析。假设各网络中每个交换机连接一个端系统,端系统esi分别与交换机swi相连接,假设端系统的风险度均为1,各端系统间无隔离需求,端系统es1~es4均发送1条广播VL,各VL的参数配置相同,为
为简化分析过程,假设VL连接的所有端系统的风险贡献度相同,风险贡献度取值为
依据式(4),则所有VL的风险度为1。
本实验选用的VL路径规划算法包括:
1) 文献[9]提出的基于遗传算法的路径优化算法(POGA),此算法直接将多播VL进行了多条单播VL简化处理。
2) 本文提出的RBPP算法,对单播VL和多播VL分别采用不同的路径规划算法。
3) RBPP-simple算法,对待规划的VL集合进行处理,将多播VL简化多条单播VL,在路径规划算法上采用RBPP算法。
比较不同网络拓扑结构下,3种算法规划后的网络所有交换机间链路的平均风险仿真结果,如图5所示。
图5 交换机间链路平均风险
Fig.5 Average risk among links between switches
由图5的仿真结果可知,对于相同的网络拓扑结构,对多播VL进行简化处理的POGA和RBPP-simple算法,与RBPP算法相比,网络中物理链路的平均风险增加了50%和65%。尽管RBPP-simple算法考虑了风险均衡,但由于将多播VL的简化处理造成了优化VL集合的“虚”中风险增多。如对于图1所示的4交换机网络,不同端系统间的可行链路仅有1条,对于RBPP算法,待优化的VL集合为4条广播消息,而进行简化处理后,待优化的VL集合为16条单播VL,将多播VL的风险进行了“倍增”,因此物理链路承载了“虚”风险。综上对涉及安全关键系统的AFDX网络,不能将多播VL简单的拆分为单播VL进行路径规划。
4.3 实验2
本实验详细描述RBPP算法各步骤的实现情况,以图3所示的典型AFDX网络拓扑进行风险均衡实验,对比RBPP与负载均衡(LB)、最短路径(SP)算法。假设:
1) 端系统es1~es8分别与交换机sw1~sw8相连接。
2) 各端系统仅与1个分区相连,且各分区驻留1个航电系统功能,各航电系统功能的各级失效状态数量如表1所示,其中端系统es3和es7需完全隔离,即
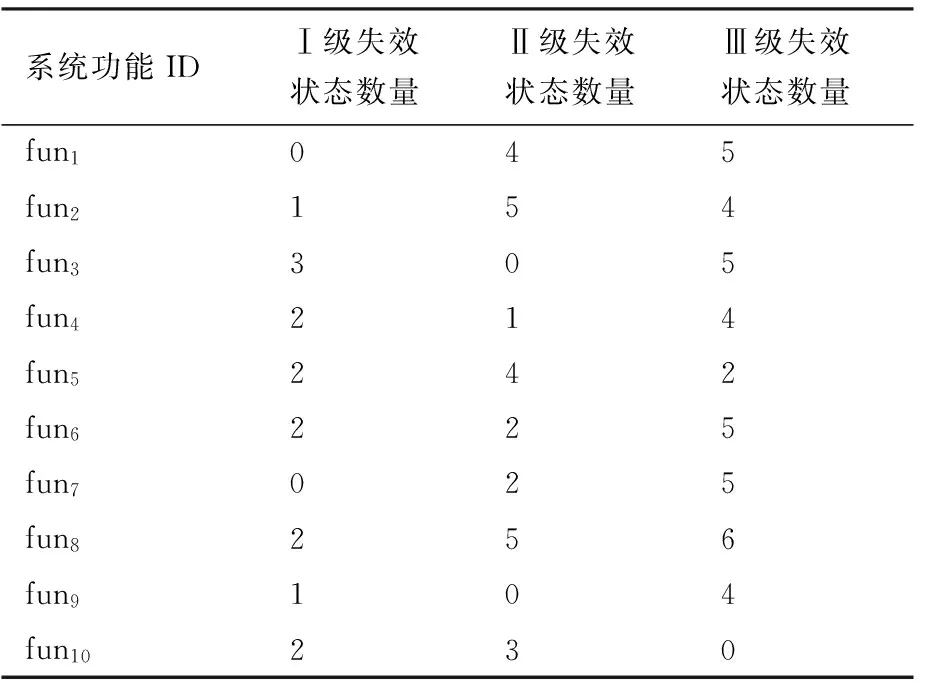
表1 端系统失效状态清单Table 1 List of failure conditions of end system
航电功能与分区及端系统的对应支持关系如表2所示。
航电系统功能风险度计算采用不同级别失效风险度差异赋值方式,w1=100,w2=10,w3=1。取RⅠ=180,RⅡ=40,RⅢ=8,对端系统esk=1/p取εk=1/p,p为共享端系统esk的分区数量。依据式(1)~式(3)计算可得各航电系统功能、分区及端系统的风险度如表3,其中es1所服务的分区中航电功能失效状态最高为Ⅱ类,因此其风险度不应超过RⅡ,es1所服务的分区中航电功能失效状态最高为 Ⅰ 类,因此其风险度不小于RⅠ。
在网络中配置7条VL,源节点分别为es1、es2、es3、es4、es5、es7和es8目的节点均为es6,所有VL的最大包长Lmax=500 byte,TBAG=4 ms,消息传输允许延迟1 ms,优先级均为1,由端系统计算得到的VL风险度如表4。
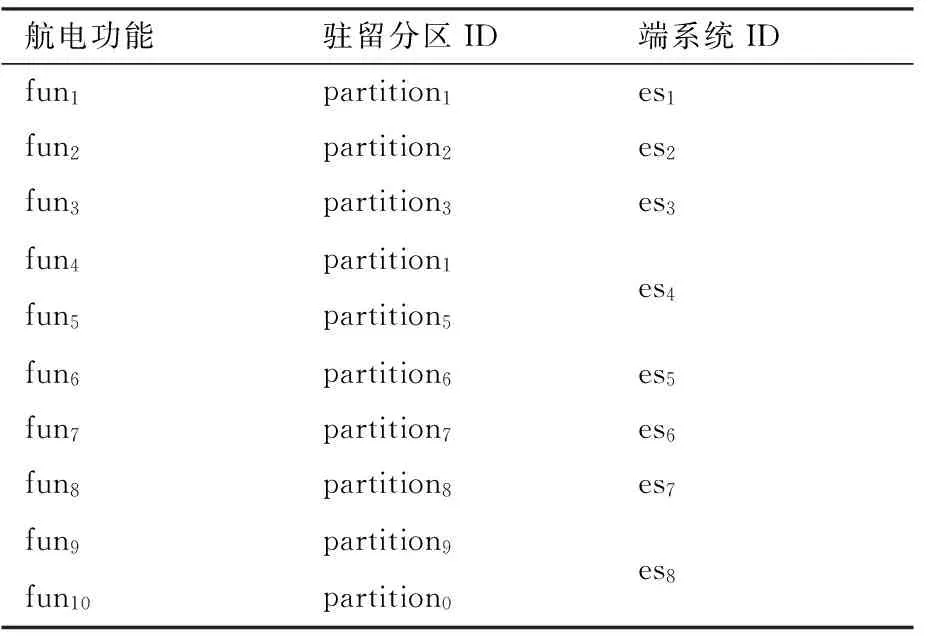
表2 驻留应用与端系统分区关系
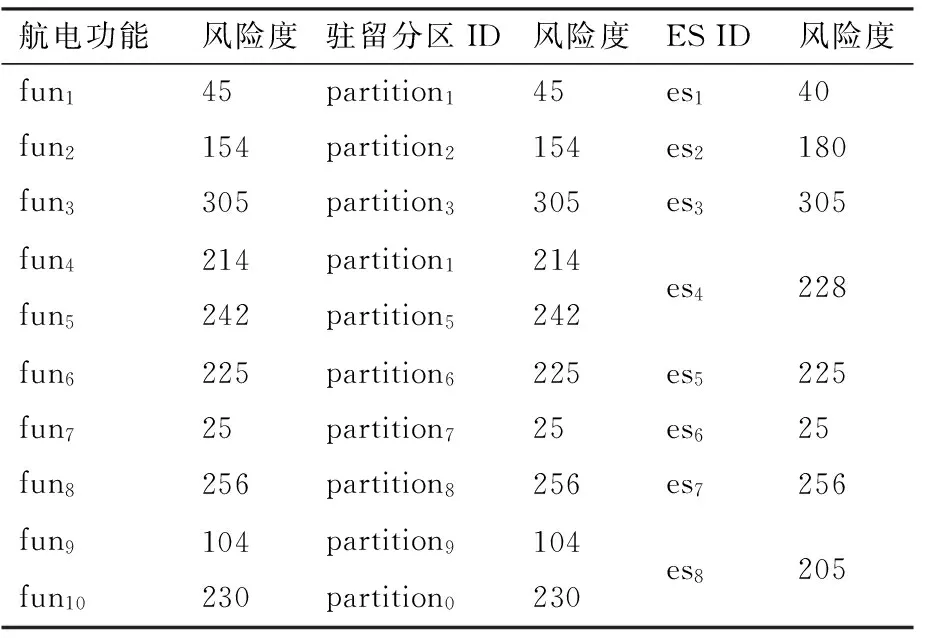
表3 端系统风险度Table 3 Risk of end system
分别采用SP算法、LB算法和本文提出的RBPP算法进行路径规划,本实验中,通信流量较少,3种算法均无超时消息。3种算法得到的路径规划如表5。
分析各算法路径规划后,全网物理链路的风险方差为
σSP=142.3,σLB=111.6,σRBPP=107.1
可知,σSP>σLB>σRBPP,即RBPP算法的风险均衡能力最好,最短路径算法能力最差。分析原因为,最短路径算法以最小跳为优化目标,未考虑VL信息的特性;LB算法以在各物理链路中均衡流量负载为目标,在分散流量的同时具有一定的风险均衡能力;RBPP算法以物理链路间的风险均衡为目标,因此其风险均衡能力最强。
对于端系统的隔离能力,端系统es3和es7需完全隔离,因此所有的物理路径不应同时承载vl3和vl7,由表5可知,SP和LB算法规划后,链路sw6-sw7承载了vl3和vl7,违反了端系统隔离需求,RBPP算法在执行优化算法时,进行了路径的隔离性检查,可满足要求。

表4 VL风险度Table 4 Risk of VL
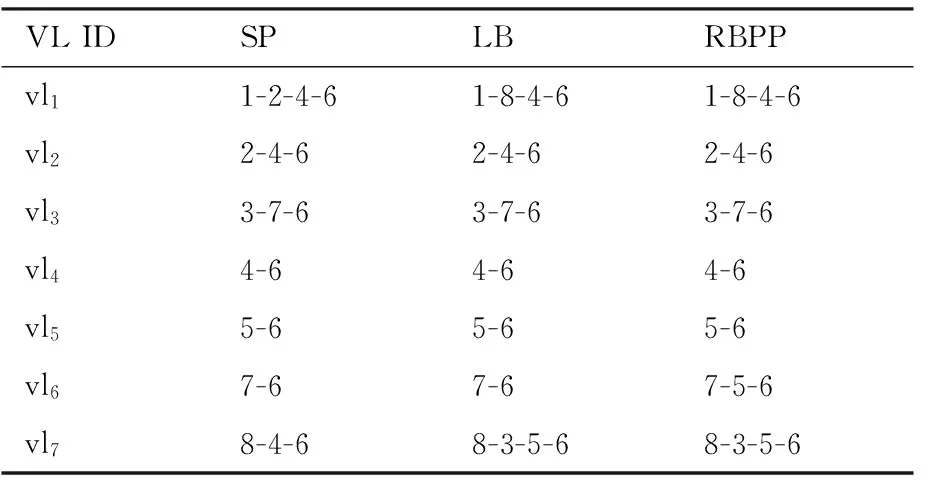
表5 不同算法路径规划结果Table 5 Results of path planning for different algorithms
4.4 实验3
本实验在图3、图4所示的网络中配置中等规模的流量,对比RBPP、LB、SP 3种AFDX路径规划算法的性能。对两种不同的网络架构各配置1 000条单播VL,配置信息如表6。
图3和图4中具有相同标识的端系统具有相同风险度,采用表3的风险度取值,补充端系统es9的风险度为70。端系统间的隔离需求矩阵如表7,即端系统es3和es5需完全隔离,es2和es3,es1和es7,es4和es6间有限的隔离,其他节点间无隔离需求。
采用RBPP、LB、SP 3种算法进行虚拟链路规划,计算不同算法下全网物理链路的风险方差σ,仿真结果如表8所示,3种算法在两种网络拓扑条件下均无超时消息。
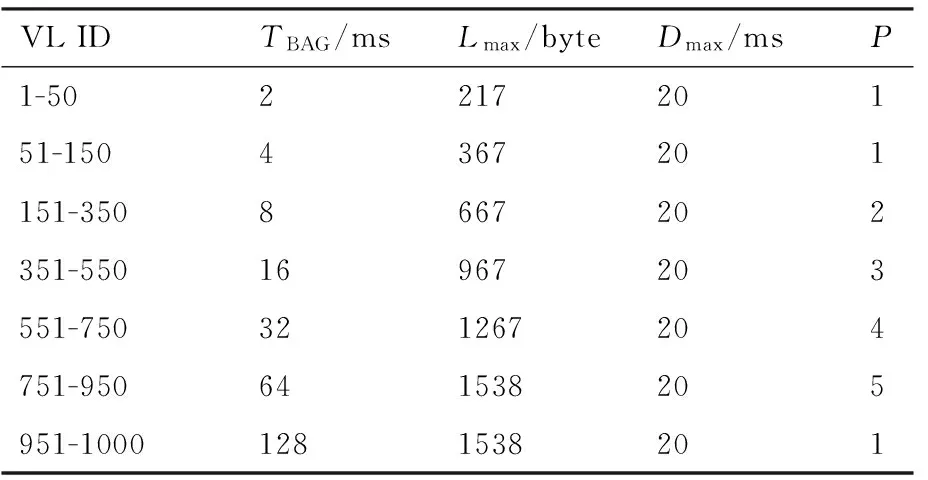
表6 VL配置信息Table 6 Information of VL
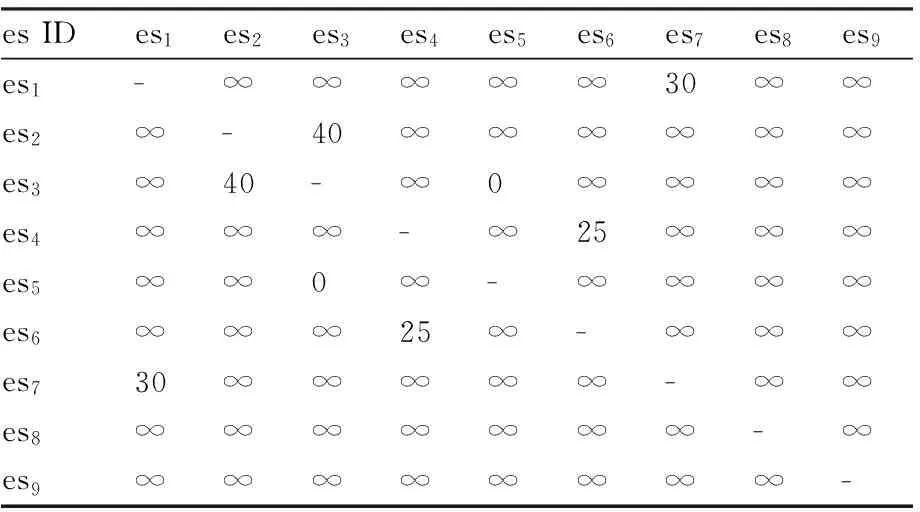
表7 端系统隔离需求Table 7 Isolation requirement of end system
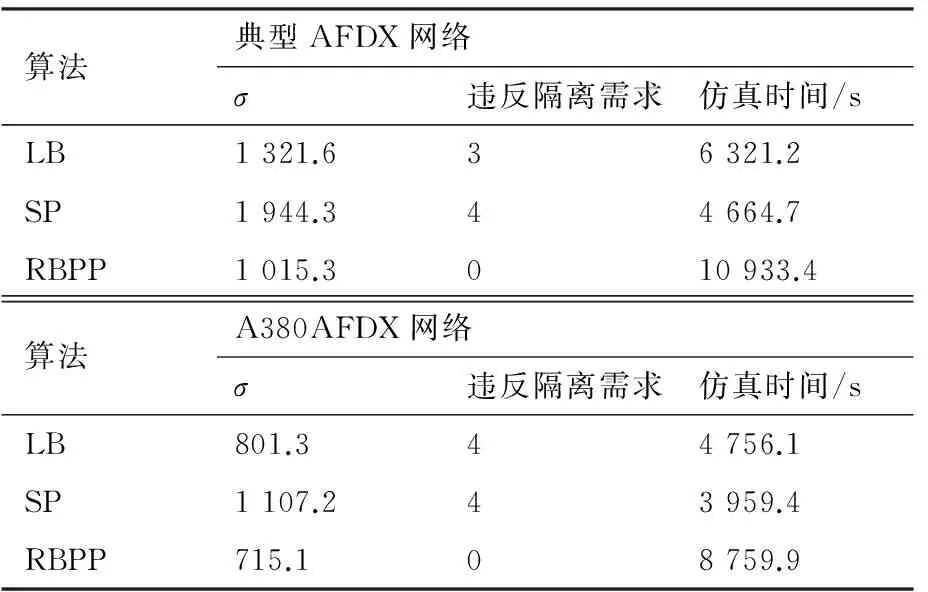
表8 仿真结果Table 8 Simulation results
由仿真结果可知,在中等规模流量条件下,两种网络拓扑结构下,RBPP算法的风险均衡能力比LB算法分别提高了10.7%和23.4%,比SP算法分别提高了35.4%和47.9%。
对于端系统的间隔离需求,SP算法仅考虑了网络中各节点的连通性,未考虑传输消息包含的信息,路径规划仅关注VL传输路径跳数,因此在两种拓扑网络中对端系统间隔离需求均未能满足;LB算法考虑了传输消息的流量信息,具有一定的路径均衡能力,但主要考虑的是传输流量,因此在两种拓扑网络中种仅在典型AFDX网络结构中满足了es2和es3相关的VL共享物理路径不超过40条的隔离需求;RBPP算法以满足端系统隔离需求,同时均衡各物理链路风险为目标,因此,在两种网络中都能满足端系统隔离需求。但是由于要满足端系统隔离需求,在进行风险均衡时的部分VL的可用路径变少,使得各链路间的风险偏差提高,如在网络链路相对较少的A380AFDX网络拓扑中,RBPP算法优化后的网络链路间风险偏差与LB相近。
对于算法效率,由于RBPP算法首先对各VL进行最短路径求解,然后对VL集合进行粒子群优化,其算法执行时间远高于LB和SP。另外对于网络中可用链路相对较少的网络,单次PSO优化得到的结果可能不满足隔离需求,因此需要多次执行优化算法,算法执行时间有可能会高于网络拓扑复杂的网络。如在本实验中,虽然A380AFDX网络与典型AFDX网络相比网络拓扑结构相对简单,但是RBPP算法执行时间更长。
5 结 论
1) 为保证IMA的系统级隔离要求,提出了一种面向风险均衡的AFDX网络VL路径规划算法RBPP,以均衡各物理链路间的风险为优化目标,提高系统安全性。
2) 给出了端系统、VL和物理链路的风险度计算方法,引入PSO算法进行VL路径规划,与最短路径算法和流量均衡算法相比,可有效分散风险;同时端系统隔离性检查可有效满足系统级隔离需求。
3) 目前采用的RBPP求解算法,在路径规划后进行隔离性检查,对不满足的路径集合进行重规划,效率较低,下一步研究计划将隔离性检查在路径规划过程工实现,以提高计算效率。
[1] 熊华钢, 王中华. 先进航空电子综合技术[M]. 北京: 国防工业出版社, 2009: 10-12.
XIONG H G, WANG Z H. Advanced integrated avionics technology[M]. Beijing: National Defence Industry Press, 2009: 10-12 (in Chinese).
[2] SUCCA M, BOSCOLO I, DROCCO A, et al. IXV avionics architecture: Design, qualification and mission results[J]. Acta Astronautica, 2016, 124: 67-78.
[3] 王国庆, 谷青范, 王淼, 等. 新一代综合化航空电子系统构架技术研究[J]. 航空学报, 2014, 35(6): 1473-1486
WANG G Q, GU Q F, WANG M, et al. Research on the architecture technology for new generation integrated avionics system[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1473-1486 (in Chinese).
[4] CHA Y J, LIM J H, LEE S Y, et al. New feasible grouping algorithms for virtual link in AFDX networks[C]∥International Conference on Informatics, Electronics and Vision, 2015: 1-4.
[5] BAKER K. Filling the FAA guidance and policy gap for systems integration and safety assurance[C]∥IEEE Digital Avionics Systems Conference.Piscataway,NJ: IEEE Press, 2011: 1B4-1-1B4-4.
[6] SPITZER C R. The avionics handbook[M]. Boca Raton, FL: CRC Press, 2001: 155-158.
[7] BAUER H, SCHARBARG J L, FRABOUL C. Improving the worst-case delay analysis of an AFDX network using an optimized trajectory approach[J]. IEEE Transactions on Industrial Informatics, 2010, 6(4): 521-533.
[8] 赵露茜, 李峭, 林晚晴, 等. 基于随机网络演算的TTE网络时延分析[J]. 航空学报, 2016, 37(6): 1953-1961.
ZHAO L X, LI Q, LIN W Q, et al. Stochastic network calculus for analysis of latency on TTEthernet network[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1953-1961 (in Chinese).
[9] 代真, 何锋, 张宇静, 等. AFDX虚拟链路路径实时寻优算法[J]. 航空学报, 2015, 36(6): 1924-1932.
DAI Z, HE F, ZHANG Y J, et al. Real-time path optimization algorithm of AFDX virtual link[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1924-1932 (in Chinese).
[10] FRANCES F, FRABOUL C, GRIEU J. Using network calculus to optimize the AFDX network[J]. IEEE Transactions on Medical Imaging, 2006, 25(10): 1319-1328.
[11] 刘成, 李航, 何锋, 等. 基于轨迹方法的AFDX网络路由配置算法[J]. 北京航空航天大学学报, 2012, 38(12): 1587-1590, 1595.
LIU C, LI H, HE F, et al. Routing algorithm of AFDX network based on trajectory approach[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(12): 1587-1590, 1595 (in Chinese).
[12] WU Z, HUNG N, LI R, et al. A delay reliability estimation method for avionics full duplex switched Ethernet based on stochastic network calculus[J]. Eksploatacja i Niezawodnosc-Maintenance and Reliability, 2015, 17(2):288-296.
[13] ZHANG Y T, HUANG Z, XIONG H G. Study on network reliability in avionics based on performance degradation constraints[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1461-1468.
[14] Federal Aviation Administration. Advisory Circulars: AC 20-156 aviation databus assurance[S]. Washington, D.C.: Federal Aviation Administration, 2006.
[15] AN D, KIM K H, KIM K I. Optimal configuration of virtual links for avionics network systems[J]. International Journal of Aerospace Engineering, 2015, 11(8): 1-9.
[16] 冯晓林, 戴卫兵, 彭国金. C919飞机航空总线采集和实时分析技术[J]. 飞行力学, 2016, 34(5): 73-76.
FENG X L, DAI W B, PENG G J, Avionic bus collection and real-time analysis techniques of C919[J]. Flight Dynamics, 2016, 34(5): 73-76 (in Chinese).
[17] Society of Automotive Engineers. Guidelines and methods for conducting the safety assessment process on civil airborne systems and equipment: ARP4761[S]. Troy Michigan: Society of Automotive Engineers,1996.
[18] Aeronautical Radio Inc.. Aircraft data network part 7 avionics full-duplex switched Ethernet network: ARINC664-P7[S]. Annapolis: Aeronautical Radio Inc., 2009.
[19] LIU C, WANG T, ZHAO C X, et al. Worst-case flow model of VL for worst-case delay analysis of AFDX[J]. Electronics Letters, 2012, 48(6): 327-328.
[20] EBERHART R C, KENNEDY J. A new optimizer using particle swarm theory[C]∥Proceedings of The Sixth International Symposium on Micro Machine and Human Science. Piscataway, NJ: IEEE Press, 2002: 39-43.
[21] XU F, CHEN H, GONG X, et al. Fast nonlinear model predictive control on FPGA using particle swarm optimization[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 310-321.
[22] LIANG J J, QIN A K, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295.
[23] CRAUSER A, MEHLHORN K, MEYER U, et al. A parallelization of Dijkstra’s shortest path algorithm[M]. Berlin: Springer, 1998: 722-731.
[24] FURER M, RAGHAVACHARI B. Approximating the minimum-degree steiner tree to within one of optimal[J]. Journal of Algorithms, 1994, 17(3): 409-423.
[25] SHI Y, EBERHART R C. Parameter selection in particle swarm optimization[C]∥Proceedings of the 7th International Conference on Evolutionary Programming Ⅶ, 1998: 591-600.
[26] 黄臻, 张勇涛, 熊华钢. 基于离散事件方法的AFDX建模与仿真[J]. 北京航空航天大学学报, 2011, 37(10): 1326-1332.
HUNG Z, ZHANG Y T, XIONG H G.AFDX modeling and simulation based on discrete event method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(10): 1326-1332 (in Chinese).
[27] CHARARA H, SCHARBARG J L, ERMONT J, et al. Methods for bounding end-to-end delays on an AFDX network[C]∥2006 Euromicro Conference on Real-Time Systems. Piscataway, NJ: IEEE Press, 2006.
[28] ITIER J B. A380 integrated modular avionics[C]∥Proceedings of the ARTIST2 Meeting on Integrated Modular avionics, 2007.

