飞机壁板自动钻铆机气动送钉技术
蒋君侠,张启祥,朱伟东
浙江大学 机械工程学院,杭州 310027
铆接作为飞机装配中的重要连接形式极大地影响着飞机寿命[1-4],航空业发达国家普遍采用自动钻铆技术以提高飞机壁板钻铆的质量和效率。西方极少数国家拥有先进的自动钻铆技术并能够制造出自动钻铆设备[5-9],但由于技术封锁原因出口到中国的大都是国外淘汰的自动钻铆机。随着国产大飞机项目的开展,急需进行自动钻铆技术研究和设备的自主研发。作为自动钻铆机的重要组成部分,送钉系统主要依据设备的结构和功能而设计,实现铆钉储存和输送的功能[10-11]。国外自动钻铆机如BROTJE的MPAC[12]、EI(Electroimpact)的E7000[13]和GEMCOR的G2000等都配备了由法国AHG公司研发的抽屉式送钉系统[14],这种系统由预先储存好不同型号铆钉的多个抽屉组成,每个抽屉存储大量铆钉并放置在抽屉架上,系统自动控制从抽屉选钉然后进入输送管道送至钻铆头终端。
自动钻铆机运动复杂,配套送钉系统多选用具有较好灵活性的软管作为输送管道,并采用气力输送,但在选择输送管道内径和输送气压时多依靠经验选取,缺少深入理论研究。国内有高校[15-17]对输送管道的最小弯曲半径和最小输送气压作了一定研究,实际在设计送钉系统时更重要的是如何确定最佳的输送管道内径和管道入口输送气压,这也是本文的主要研究内容。本文先对送钉系统和铆钉在输送管道中的运动作了介绍和分析,然后根据沉头铆钉外形,分别对输送管道内径的选择方法和输送气压的计算方法进行深入研究,最后结合自动钻铆机配套的送钉系统进行试验验证。送钉技术理论研究和工程试验为送钉系统的设计提供了可靠的依据。
1 送钉系统

图1 自动钻铆机和送钉系统Fig.1 Automatic drilling and riveting machine & rivet feeding system
如图1所示为作者参与研发的飞机壁板自动钻铆机,图中右侧为配套的送钉系统。送钉系统主要由铆钉柜、铆钉注射器、铆钉插钉器和铆钉输送管道组成。铆钉柜安装在钻铆机底部滑枕上跟随钻铆机移动,铆钉注射器和铆钉插钉器安装在钻铆机制孔插钉头上,铆钉输送管道安放在自动钻铆机内部,一端连接铆钉柜、另一端连接铆钉注射器。送钉系统具体工作流程为,铆钉柜输出铆钉进入输送管道,铆钉在输送气流的作用下沿管道输送至铆钉注射器,再由注射器送至插钉器,最后由插钉器将铆钉插入铆接孔。
送钉系统输送管道的主要特点:① 线路长,飞机壁板自动钻铆机尺寸大,安装在底部滑枕上的铆钉柜与制孔插钉头距离远,因此连接铆钉柜和铆钉注射器的铆钉输送管道需要足够长的线路;② 弯道多,为了降低对自动钻铆机工作的干扰,输送管道安放在钻铆机内部空隙区域,不可避免地产生许多弯曲部分;③ 路径多变。自动钻铆机工作运动复杂,空间状态变换多,输送管道的路径相应会发生许多变化。
输送管道线路长、弯道多、路径多变等特点,使得铆钉输送成为送钉系统中最容易发生故障的环节。所以在选择输送管道内径和确定管道入口输送气压时必须考虑铆钉的运动情况。
2 输送管道中铆钉运动分析
工程中输送管道是在三维空间铺设,但主要以直线路径和平面内的弯曲路径为主,三维曲线路径情况较少且距离不长,所以整体管道路径可简化为平面内的直线路径和弯曲路径。管道中每次仅输送一个铆钉,保证气源稳定的前提下,可认为铆钉为稳定输送。因此研究时按铆钉在平面内的稳定运动状态进行分析。
2.1 直管道中铆钉的运动
沉头铆钉和其在倾斜角度φ的直管道中输送受力情况如图2所示。其中D为铆钉沉头直径,d为铆钉公称直径,H为铆钉沉头高度,L为铆钉总长度,B为管道内径;v为输送气流速度,u为铆钉速度;γ为铆钉沉头面与气流速度方向垂面的夹角,AD为铆钉在气流速度方向的投影面积;F为输送铆钉的气动力,与铆钉速度方向相同;f为铆钉受摩擦力,FN为铆钉受管道内壁支持力,mg为铆钉重力;m为铆钉质量。
由图2可得铆钉详细受力分析为
(1)
式中:μ为铆钉与管道内壁间的摩擦系数,气动力F为[18-19]
(2)
(3)
式中:C为动力系数;ρ为输送气流密度;ω为与具体输送情况有关的系数。
式(2)和式(3)表明动力系数C影响气动力大小,且管道内径B越小则动力系数C越大。
联立式(1)和式(2)得
(4)
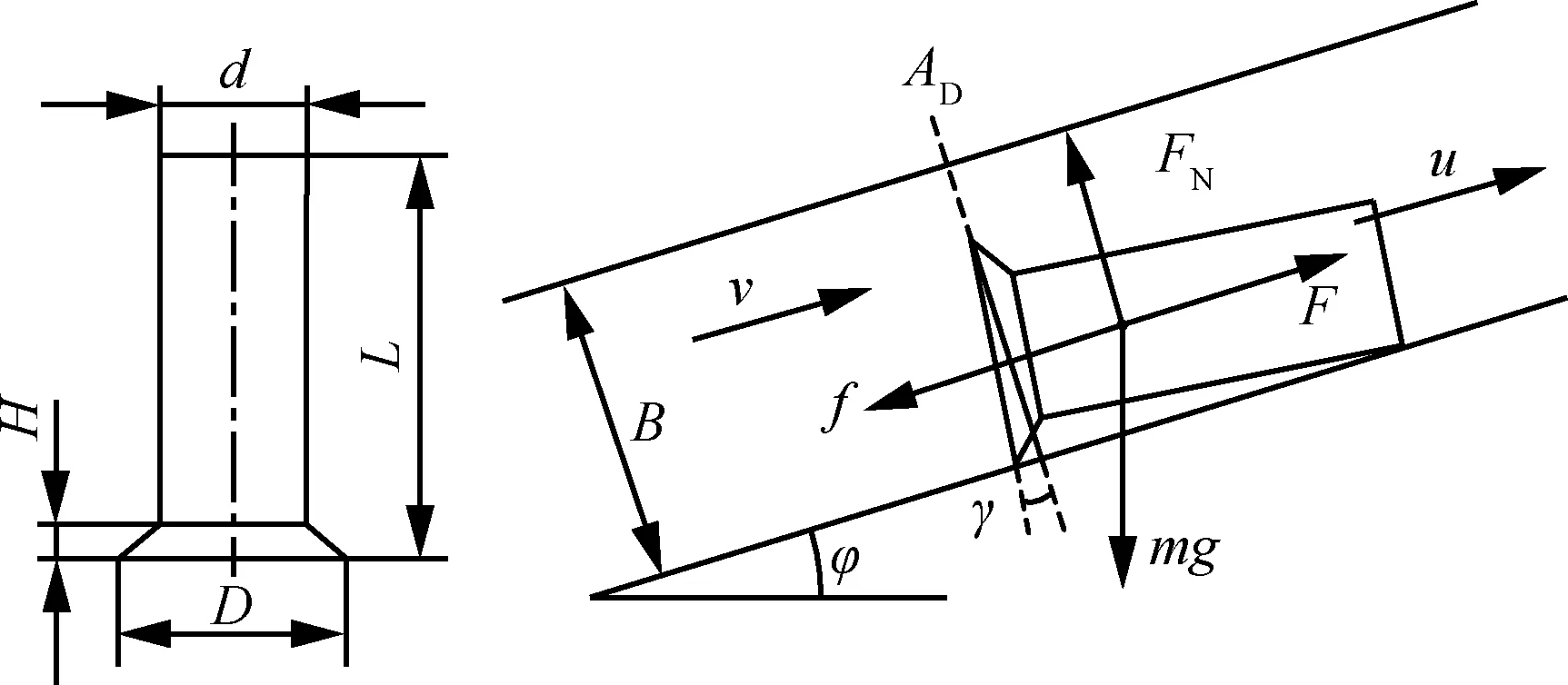
图2 铆钉及其在直管道中的受力分析Fig.2 Rivet and analysis of forces in straight tube
铆钉输送需满足du/dt≥0,代入式(4)得
(5)
另外有
(6)

将式(6)代入式(5)得
(7)
当铆钉速度u=0时可得
(8)
由此可得直管道中输送铆钉所需的最小气流速度为
(9)
当铆钉速度u≠0时可得
(10)
由此可得直管道中铆钉可达到的最大速度为
(11)
2.2 弯管道中铆钉的运动

图3 铆钉在弯管道中的受力分析Fig.3 Force analysis of rivet in bending tube
铆钉在弯管道中输送最不利的情况是由水平转为竖直向上,此时铆钉按照重心进行受力分析如图3所示。其中φ为铆钉受支持力与垂直方向的夹角,Ru为铆钉重心运动轨迹的弯曲半径。
由图3可得铆钉详细受力分析为
(12)
联立式(2)和式(12)得

(13)
铆钉输送需满足du/dt≥0,代入式(13)得
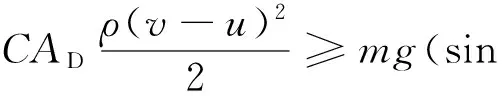
(14)
图3情况下AD近似等于铆钉沉头面积,因此同2.1节中计算方法可得弯管道中输送铆钉所需的最小气流速度为
(15)
综合式(9)和式(15)可得输送铆钉所需最小气流速度为
vmin=max(vmin1,vmin2)=vmin1
(16)
此外由式(1)和式(12)对比可知,弯管道中的摩擦力与直管道中的摩擦力相比增加了向心力的影响,导致管道弯曲处磨损较为严重。且弯管道中铆钉速度越大、弯曲半径越小,则磨损越严重。
3 输送管道内径选择方法
送钉系统针对不同型号铆钉需要选择不同内径的输送管道。对于图2所示的沉头铆钉,输送管道内径B默认选取原则为
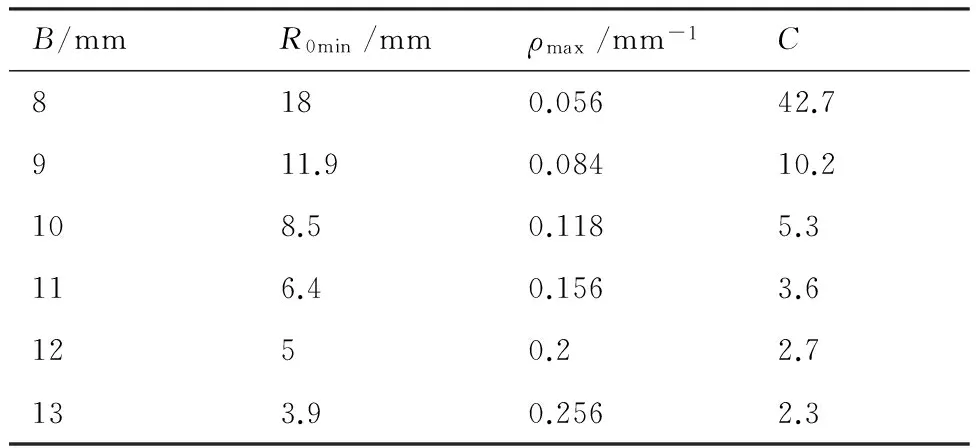
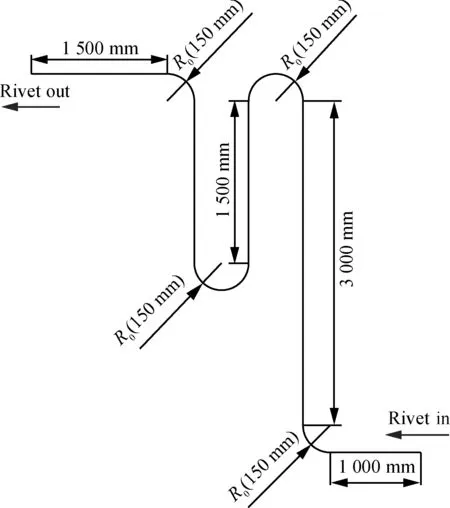
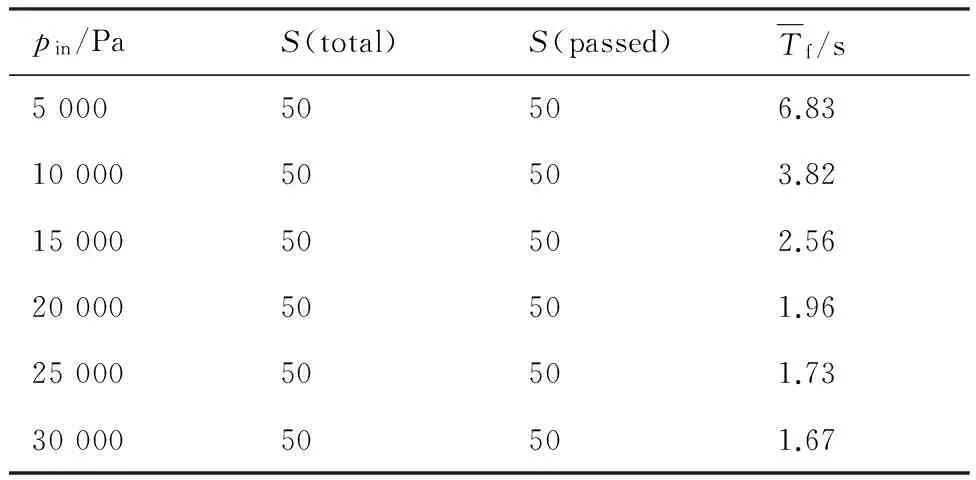
B∈{Bi}D (17) 式中:{Bi}为可选管道内径的集合。 这是因为若Bi≤D,则铆钉不能通过;若Bi≥L,则铆钉输送时将会打转翻动。此选取原则比较笼统,经常是在D~L之间靠经验选取管道内径B。送钉系统选取管道内径时,主要考虑管道弯曲时不易卡钉和铆钉受气动力较大,所以综合管道弯曲卡钉分析和动力系数两方面,从而进行管道内径的选择。 送钉系统使用的软管输送管道在一定范围内弯曲时可认为管道截面形状不变。当管道弯曲至一定程度后,沉头铆钉在其中输送将会发生卡钉。管道发生临界卡钉状态时的弯曲半径称为临界卡钉弯曲半径。管道发生卡钉有两种情况,铆钉杆与管道内壁抵触卡钉,或铆钉前端与管内壁接触区产生摩擦死角卡钉。 3.1.1 管道卡钉条件几何分析法 图4中R0为管道弯曲半径,R为管道内壁外侧弯曲半径,A1、A2为铆钉与弯管道内壁外侧的两个接触点。分别过A1和弯管曲率中心建立Oxy坐标系,则t为铆钉杆与管道内壁内侧的最小间隙,n为铆钉杆与弯管曲率中心的最大垂直距离。圆弧A1A2在坐标系Oxy中的方程为 x2+(y+n)2=R2 (18) 令x1=OA1,根据铆钉尺寸可得A1、A2坐标分别为A1(x1,0)、A2(x1-L,(D-d)/2),代入式(18)可得 (19) 由式(19)解得 (20) 同时由图4可知 图4 铆钉和弯曲管道Fig.4 Rivet and bending tube (21) 联立式(20)和式(21)解得 (22) 式中: t=0时可计算得管道临界卡钉弯曲半径R0min1。 3.1.2 管道卡钉条件力学分析法 铆钉前端与管内壁接触区的摩擦角θ如图5所示。 为避免出现摩擦死角而卡钉,须满足 Fsinθ>μFcosθ (23) 同时由图5中三角关系可知 (24) 联立式(21)、式(23)和式(24)解得 (25) 所以管道临界卡钉弯曲半径为 (26) 综合可得为了避免铆钉在输送管道弯曲处卡钉,管道最小弯曲半径应为 R0min=max(R0min1,R0min2) (27) 图5 铆钉与管道的摩擦角Fig.5 Frictional angle between rivet and tube 引入最小弯曲半径R0min对应的最大弯曲曲率ρmax,由式(22)、式(26)和式(27)可知管道内径B越大则最大弯曲曲率ρmax越大越有利;由式(3)可知管道内径B越大则动力系数C越小越不利。因此在已知管道内径选择范围{Bi}时,令M等于ρmax与C的无量纲相对值的差值绝对值,取M最小时对应的管道内径Bi,此时管道最大弯曲曲率ρmax和动力系数C综合情况最好,最有利于铆钉输送。所以可得最优管道内径B综合选择方法为 (28) 工程中常使用同一管道输送沉头直径D、公称直径d和沉头高度H相同但长度L不同的系列铆钉。针对D=7.26 mm,d=5 mm,L=14~20 mm系列铆钉,按照管道内径默认选取原则其选择范围为7.26 mm 由表1数据根据式(28)作出M=f(Bi)的曲线,结果如图6所示。 表1不同管道内径下的最小弯曲半径和阻力系数 Table1Minimumbendingradiusesanddragcoefficientsintubeswithdifferentinteriordiameters B/mmR0min/mmρmax/mm-1C8180.05642.7911.90.08410.2108.50.1185.3116.40.1563.61250.22.7133.90.2562.3 图6 最佳管道内径选择曲线Fig.6 Curve for selection of optimum tube interior diameter 图6表明,B=9时M=f(Bi)达到最小值,所以B=f-1(M)|Mmin=9,此时管道最大弯曲曲率ρmax和动力系数C的无量纲相对值最接近,输送管道弯曲不卡钉和铆钉受气动力综合情况最好,所以最优管道内径为B=9 mm。同理可扩展,B=9 mm对于D=7.26 mm,d=5 mm,L=10~20 mm系列铆钉是最优输送管道内径。 送钉系统是在管道铆钉入口施加一定气压靠气力输送铆钉。输送过程中存在各种压强损失,入口气压不足则不能顺利送钉。同时输送气压影响输送速度,从而影响铆钉输送时间。所以从输送过程压强损失、铆钉输送时间两方面来计算管道入口输送气压。 图7 铆钉输送路径Fig.7 Path of rivet feeding 铆钉输送路径如图7所示,pin为入口压强,pout为出口压强,本文所述压强均为相对压强。气力输送铆钉过程中不可避免地存在压强损失,主要包括3部分:沿程压强损失、送钉压强损失和弯道压强损失[20]。 4.1.1 沿程压强损失Δp1 气流在管道中流动时,管壁的粘附作用和气流内部之间的摩擦力将沿流程阻碍气流流动,从而产生沿程压强损失。在图7所示情况下沿程压强损失为 (29) 式中:λ为沿程阻力系数;l为管道总长度。 4.1.2 送钉压强损失Δp2 当气流在截面均匀的管道内流动遇到铆钉时,气流方向和速度都会发生变化,产生的附加阻力会使气流产生送钉压强损失,如图7所示铆钉前后压强分别为p1、p2,送钉压强损失Δp2为 (30) 4.1.3 弯道压强损失Δp3 气流在管道中流经弯曲区域时,流速大小和方向被迫发生急剧变化从而产生压强损失。如图7所示的管道弯曲处前后压强分别为p3、p4,弯道压强损失Δp3为 (31) 式中:ζ为局部阻力系数,其表达式为 (32) 式中:ψ为弯道弯曲角度。 所以可得铆钉输送全程压强损失Δp为 Δp=pin-pout= Δp1+Δp2+Δp3= (33) 流体力学中管道某处的压强等于该处的静压与动压之和。实际送钉气流速度较小可认为气流不可压缩,所以输送管道出口与入口流速相同。管道出口处静压pout(s)=0,动压pout(d)与流速相关,所以出口压强pout、入口压强pin分别为 (34) pin=pout+Δp= (35) 设自动钻铆机钻铆速率为N,即为一分钟内完成钻铆工作的铆钉数量。在一个钻铆周期中包括铆钉输送时间Tf、制孔时间Td和铆接时间Tr等,即 (36) 本文所提的送钉是指铆钉从钉柜中输出至铆钉注射器这段过程,因此为了保证钻铆机的钻铆速率,保守铆钉输送时间需满足 (37) (38) 假定铆钉平均输送速度与可达最大速度umax关系为 (39) 式中:η为铆钉速度有效系数,依具体情况而定。 联立式(11)、式(37)~式(39)可得为满足铆钉输送时间所需的气流速度为 (40) 将式(40)代入式(35)可得管道入口理论输送气压pin-cal为 (41) 针对D=7.26 mm,d=5 mm,L=12 mm的铆钉,按照管道内径默认选取原则可选内径B∈{8,9,10,11} mm,按照管道内径选择的理论研究应选内径9 mm。所以选择同种材质、内径分别为8、9、10 mm的输送管道按图8路径进行送钉试验,管道入口施加10 000 Pa气压,该气压值足够大以输送铆钉。改变弯曲半径R0并统计铆钉通过情况和输送时间,结果如表2所示。 由表2可知当弯曲半径为8~10 mm时,内径8 mm的管道会发生卡钉,内径9 mm和10 mm的管道则不会发生卡钉,考虑到实际输送管道会发生截面弯曲变形,故弯曲半径不会比8 mm更小,所以9 mm和10 mm内径的管道更利于顺利送钉;此外在等气压输送情况下内径9 mm管道比内径10 mm管道输送时间更短,即说明前者比后者送钉动力系数大,更利于铆钉输送。综合可得内径9 mm管道对于输送试验铆钉最为合适,也证明了前文管道内径综合选择方法的合理性。 图8 管道内径选择试验路径Fig.8 Experimental path for choosing interior diameter of tube 表2 管道内径选择试验结果Table 2 Experimental results for choosing interior diameter of tube R0/mmS(total)S(passed)Tf/sB=8mmB=9mmB=10mmB=8mmB=9mmB=10mmB=8mmB=9mmB=10mm8505050050501.191.39105050503550500.811.011.25125050505050500.580.931.07 为了配合工程需要,管道入口输送气压验证的试验将在作者参与研发的自动钻铆机上进行,如图9所示。配套送钉系统的铆钉柜安装在钻铆机右侧滑枕上的箱罩内,铆钉输送管道安放在钻铆机内部,为了配合制孔插钉头的大范围多自由度运动,输送管道的安放路径如图9中黄线所示。 针对D=7.26 mm,d=5 mm,L=12 mm的铆钉,根据输送管道内径选择的研究可知内径为9 mm 输送管道最为合适。对于图9自动钻铆机的送钉系统,整体输送管道是在三维空间铺设,但直线段管道都可按平面路径计算,且弯曲段管道也多是在平面内弯曲,因此整体输送管道可简化为平面内管道。制孔插钉头运动至最高处时铆钉输送最不利,此时铆钉输送管道路径近似为如图10所示。实际自动钻铆机钻铆速率N=10,由式(37)可得输送时间Tf≤2 s。鉴于图10输送管道路径的复杂性,保守铆钉速度有效系数η=1/2。所以由式(41)可得管道入口理论输送气压为pin-cal≥17 917 Pa。 按图10路径进行输送气压验证试验,通过减压阀改变管道入口输送气压,结果如表3所示。 由表3可知气压在不小于20 000 Pa的情况下铆钉输送时间符合预期结果Tf≤2 s,所以实际所需输送气压pin-act≥20 000 Pa,接近理论输送气压pin-cal≥17 917 Pa,说明前文管道入口理论输送气压计算方法是合理的。理论值与实际值存在误差的原因可能是在压强损失计算中公式相对于实际情况有所简化,从而导致理论值比实际值略小。尽管如此,理论计算方法对实际确定管道入口输送气压仍然具有很大的指导作用。 图9 钻铆机送钉路线Fig.9 Rivet feeding path of drilling and riveting machine 图10 输送气压选择试验路径Fig.10 Experimental path for choosing feeding air pressure 表3 输送气压选择试验结果 Table 3 Experimental results for choosing feeding air pressure pin/PaS(total)S(passed)Tf/s500050506.831000050503.821500050502.562000050501.962500050501.733000050501.67 图10所示铆钉输送路径是最不利的送钉情况,所以实际选用气压pin-act=20 000 Pa也能满足其他路径的送钉需求,对于自动钻铆机送钉系统而言是最佳的管道入口输送气压。 1) 通过几何分析法和力学分析法,得出管道最小弯曲半径计算公式,并综合送钉动力系数得出最优管道内径选择方法。针对直径为5 mm的不同长度铆钉,得出最优管道内径为9 mm。针对∅5 mm×12 mm铆钉,试验表明内径为9 mm时管道弯曲不卡钉和铆钉受气动力综合情况最好,是最优管道内径。 2) 采用流体力学和空气动力学计算铆钉输送压强损失,结合输送时间和速度分析得出合适输送气压计算方法。针对作者参与研发的飞机壁板自动钻铆机的送钉系统,选用∅5 mm×12 mm铆钉和最优内径管道进行送钉试验,试验得出的合适输送气压与理论计算结果较为接近,证明了理论方法的合理性。 本文中关于送钉技术的研究对其他送钉系统输送不同型号铆钉也同样适用,对设计送钉系统并提高其工作效率和稳定性等有着明显的指导作用。 [1] 王巍, 俞鸿均, 谷天慧. 大型飞机壁板组件先进装配技术[J]. 航空制造技术, 2016(5): 42-46. WANG W, YU H J, GU T H. Advanced assembly technology of large aircraft panel components[J]. Aeronautical Manufacturing Technology, 2016(5): 42-46 (in Chinese). [2] 杜兆才, 姚艳彬, 王健. 机器人钻铆系统研究现状及发展趋势[J]. 航空制造技术, 2015(4): 26-31. DU Z C, YAO Y B, WANG J. Research status and development trends of robot drilling and riveting system[J]. Aeronautical Manufacturing Technology, 2015(4): 26-31 (in Chinese). [3] 王珉, 陈文亮, 郝鹏飞, 等. 飞机数字化自动钻铆系统及其关键技术[J]. 航空制造技术, 2013(1/2): 80-83. WANG M, CHEN W L, HAO P F, et al. Aircraft automatic drilling and riveting system and its key technology[J]. Aeronautical Manufacturing Technology, 2013(1/2): 80-83 (in Chinese). [4] 许国康. 大型飞机自动化装配技术[J]. 航空学报, 2008, 29(3): 734-740. XU G K. Automatic assembly technology for large aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 734-740 (in Chinese). [5] REMLEY D, REDIGER J, HAWORTH P, et al. Slug rivet machine installs 16 rivets per minute drill rivet shave: SAE-2009-01-3155[R]. Warrendale, PA: SAE, 2009. [6] OLSSON T, HAAGE M, KIHLMAN H, et al. Cost-efficient drilling using industrial robots with high-bandwidth force feedback[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(1): 24-38. [7] BI S S, LIANG J. Robotic drilling system for titanium structures[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(5-8): 767-774. [8] DEVLIEG R, SITTON K, FEIKERT E, et al. Once (one-sided cell end effector) robotic drilling system: SAE-2002-01-2626[R]. Warrendale, PA: SAE, 2002. [9] SARH B. Assembly techniques for space vehicles: SAE-2000-01-3028[R]. Warrendale, PA: SAE, 2000. [10] BOAD C L, COLEBOURN D. Stick fastener feed system for large variety & small quantity: SAE-2008-01-2320[R]. Warrendale, PA: SAE, 2008. [11] RINK P, GIVLER G, STANCIK B, et al. New generation automated fastener feed systems: SAE-952169[R]. Warrendale, PA: SAE, 1995. [12] 邓锋. MPAC自动钻铆机[J]. 航空制造技术, 2010(6): 26-29. DENG F. MPAC automatic drilling and riveting machine[J]. Aeronautical Manufacturing Technology, 2010(6): 26-29 (in Chinese). [13] STANSBURY E C, BIGONEY B, ALLEN R. E7000 high-speed CNC fuselage riveting cell: SAE-13ATC-0086[R]. Warrendale, PA: SAE, 2012. [14] BORNES P, BROWN M, HUBERT C, et al. Womb to tomb SPC control of fasteners from rivet manufacture to installation using existing software: SAE-2003-01-2958[R]. Warrendale, PA: SAE, 2003. [15] TIAN W, ZHOU Z F, LIAO W H. Analysis and investigation of a rivet feeding tube in an aircraft automatic drilling and riveting system[J]. International Journal of Advanced Manufacturing Technology, 2016, 82(5-8): 973-983. [16] 龚辉. 基于工业机器人平台的自动供钉系统设计研究[D]. 杭州: 浙江大学, 2012: 7-8. GONG H. Design and research of automatic rivets feeding system based on industry robots platform[D].Hangzhou: Zhejiang University, 2012: 7-8 (in Chinese). [17] 李菡. 基于双机器人协同的自动钻铆终端器及其自动供钉装置的设计与研究[D]. 杭州: 浙江大学, 2010: 32-49. LI H. Study on dual-robot-based drilling & riveting end-effector and automated rivet feeding apparatus[D]. Hangzhou: Zhejiang University, 2010: 32-49 (in Chinese). [18] 黄标. 气力输送[M]. 上海: 上海科学技术出版社, 1984: 217-229. HUANG B. Pneumatic transmission[M]. Shanghai: Shanghai Scientific & Technical Publishers, 1984: 217-229 (in Chinese). [19] 陆志良. 空气动力学[M]. 北京: 北京航空航天大学出版社, 2009: 63-65. LU Z L. Aerodynamics[M]. Beijing: Beihang University Press, 2009: 63-65 (in Chinese). [20] 侯国祥, 孙江龙, 王先洲, 等. 工程流体力学[M]. 北京: 机械工业出版社, 2006: 88-99. HOU G X, SUN J L, WANG X Z, et al. Engineering fluid mechanics[M]. Beijing: China Machine Press, 2006: 88-99 (in Chinese).3.1 管道弯曲卡钉条件分析


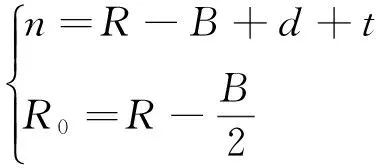


3.2 管道内径综合选择方法
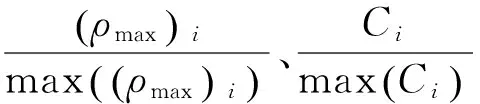
3.3 管道内径综合选择实例

4 管道入口输送气压计算方法
4.1 输送过程压强损失


4.2 管道入口理论输送气压的计算
5 试验验证
5.1 输送管道内径选择的验证



5.2 管道入口输送气压的验证

6 结 论

