欠驱动指爪机构的被动弹性元件参数优化设计

楚中毅，赖咪，燕少博

北京航空航天大学 仪器科学与光电工程学院，北京 100083

当今的太空在轨技术以及智能工业生产均离不开基于智能机器人系统的精密操作，例如，太空领域中的航天器装配、卫星维护以及工业机器人领域中的零件搬运和装配等，而末端执行器作为机器人系统最重要的组成部分之一，具有重要的研究价值。其中，欠驱动指爪机构是一类典型的末端执行器。相比于全驱动指爪，其具有更加轻便、容易控制、成本低廉的优势[1-3]，因此得到了广泛的研究[4-11]。

目前，国内外研究主要将欠驱动指爪抓取过程的自适应性及稳定性作为评价抓取性能的重要指标[12-13]。为了实现稳定抓取，文献[14]提出一种基于抓取状态平面的可视化方法以得到稳定区域，并以此为基础提出欠驱动指爪的设计准则。为表征稳定抓取并建立其解析表达式，文献[15]提出不同抓取模式指爪几何和驱动参数的设计方法。另外，楚中毅等对欠驱动指爪的不同抓取模式也进行了定量分析，并通过实验验证了其自适应性[16]。此外，Jung等分析了接触点的数量和接触力对稳定抓取的影响，接触点数量越多，接触力分布越均匀，抓取的性能就越好[17]。但是，上述方法的建模过程中忽略了被动弹性元件的影响。实际上，弹簧被动扭矩、接触力和电机驱动扭矩之间的关系决定了不同抓取模式的稳定性和自适应能力[18]。若弹簧刚度选择过小，欠驱动指爪可以更好地适应物体的形状，但其稳定性会降低；若弹簧刚度选择过大，抓取稳定性会增强，但势必影响其适应更多不规则形状物体的能力。因此，有学者开始尝试对弹簧刚度的设计进行研究，但仅限于定性地通过仿真和实验获取合适的弹簧刚度[19]。综上所述，鉴于弹簧刚度参数在欠驱动指爪设计中的重要性，有必要进行深入的研究，以期为欠驱动指爪机构的设计和控制应用奠定一定的理论和技术基础。

本文基于抓取状态平面法的思想[14]，提出一种欠驱动指爪被动弹性元件参数的优化设计方法，将弹簧刚度作为设计参数，以实现欠驱动指爪抓取稳定性与自适应性之间的平衡。首先，为了获取不同抓取模式下欠驱动指爪合适的弹簧刚度，需建立弹簧刚度与驱动力的平衡方程；然后，基于欠驱动指爪在不同抓取模式下拓扑转换的定量分析，得到不同抓取模式下弹簧刚度的取值范围。在此基础上，建立弹簧刚度与稳定区域关系的解析表达，最后基于稳定区域最大化的思想，进行弹簧刚度的最优设计。

1 欠驱动指爪静力学分析

为了研究弹簧刚度对欠驱动指爪抓取性能的影响，以欠驱动指爪一指为例进行分析。其有两个指节，分别为靠近手掌的近端指节和远离手掌的远端指节。近端指节与手掌、远端指节之间存在安装弹簧的转动关节，分别为关节1和关节2。当欠驱动指爪抓取目标物时，弹簧通过存储能量，使手指保持一定姿势；当指爪放开目标物时，弹簧则释放能量，使手指恢复到初始位姿。在抓取过程中，近端指节和远端指节分别与目标物接触。其中近端指节转动角度为θ1，长度为L1，与物体接触力为F1，接触点距关节1的距离为p1。关节1到腱线孔沿指节方向的距离为a1，垂直于指节方向的距离为b1。远端指节相对于近端指节的转动角度为θ2，长度为L2，接触力为F2，接触点距关节2的距离为p2。关节2到腱线孔沿指节方向的距离为a2，垂直于指节方向的距离为b2。腱线施加拉力Fm，线与关节1的距离为pm,欠驱动手指的受力如图1所示。

腱线拉力在关节1处产生的等效力矩为

Ta=Fmpm

(1)

关节2到腱线之间的垂直距离可通过几何关系计算得到[20]：

(2)

式中：a=L1-a1+a2cosθ2-b2sinθ2；b=b1-a2sinθ2-b2cosθ2。此时接触力为[20]

F=(JT)-1(TT)-1t

(3)

式中:F=[F1F2]T,t=[Ta-KΔθ1-KΔθ2]T为关节力矩，K为关节处弹簧刚度,Δθ1和Δθ2分别为θ1和θ2与初始值的差值，矩阵T为传动矩阵，有：

(4)

考虑到手指与目标物接触时会产生摩擦，摩擦系数为μ。因此，雅克比矩阵为

(5)

为了进一步分析欠驱动指爪机构的受力，可将关节1和关节2表示为O1和O2，并通过动力传递机构将作用在关节1和关节2处的力矩表示为T1、T2，手掌宽度为L0，其平面图如图2所示。其中O2i、θ2i和p2i为欠驱动指爪任意的初始位形。

定义力矩T2和T1的比值为

(6)

式(6)中，R与关节的真实转角有关。不失一般性，以圆柱形半径为robj的目标物为例。现假设目标物中心线与手掌中心线重合，如图3所示，其中目标物与手掌的接触力为Fpalm，Yobj为目标物圆心到手掌的竖直距离。C0、C1和C2为目标物与欠驱动指爪的接触点。当抓取达到稳定时，物体所受合外力为零。将物体受力沿竖直方向分解，可得：

Fobj,y=2F1cF1+2F2cF2+Fpalm

(7)

图1 欠驱动手指抓取目标物受力图Fig.1 Diagram of force generated in grasping object with an underactuated finger

式中：cF1=cosθ1+μsinθ1;cF2=cos(θ1+θ2)-μsin(θ1+θ2)。

其中，接触力与接触点位置、远端指节旋转角度的关系矩阵为

图2 欠驱动指爪模型Fig.2 Model of underactuated gripper

图3 目标物与手指受力图Fig.3 Force diagram of object and fingers

(8)

根据平衡方程式(3)和式(8)，结合式(6)可得：

(9)

通过式(9)可获得不同抓取模式(θ1和θ2可变)下弹簧刚度与驱动力的定量关系，进而为不同抓取模式的拓扑分析奠定基础。

2 不同抓取模式的拓扑分析

由于目标物的尺寸差异，导致稳定抓取过程中指爪与目标物的接触点不同，因此有必要分析与特定抓取模式相适应的目标物尺寸。现基于两点、三点、四点以及五点接触的不同抓取模式进行分析。

2.1 不同抓取模式下的目标物尺寸分析

考虑到一般的接触情况，目标物与手指的接触状态如图3所示。当欠驱动指爪的几何尺寸一定时，可抓取目标物的尺寸在一定范围内。现将基于文献[15]对不同抓取模式下目标物的半径进行讨论。

由图3可得到：

(10)

(11)

式中：SF1=cos (θ1+θ2);SF2=sin (θ1+θ2)。

当手指尺寸满足L0≤L1≤L0+L2时才可能产生五点接触。如图3所示，五点接触时Yobj=robj。当远端指节竖直时，可抓取的目标物尺寸达到最大，有θ1+θ2=π/2。将其代入式(11)，此时目标物的尺寸范围为

(12)

当手指尺寸满足L1>L0时可能产生四点接触，有Yobj>robj。此时目标物的尺寸范围为

robj,4≤

(13)

其中，

(14)

(15)

当手指尺寸满足L1≤L0+L2时可能产生三点接触，有Yobj=robj和θ1+θ2=π/2。将其代入式(11)，此时目标物的尺寸范围为

(16)

两点接触时远端指节处于竖直状态，当目标物与近端指节或手掌处于临界接触状态时，可抓取目标物的尺寸达到最大，因此有：

(17)

对于两点接触，其目标物尺寸必须大于一定的范围，该范围满足：

(18)

给定欠驱动指爪的几何尺寸，可得到不同抓取模式下目标物的尺寸范围，现就不同抓取模式之间的转换进行分析。

2.2 不同抓取模式的转换

在欠驱动指爪抓取过程中，根据弹簧被动扭矩与驱动力矩之间不同的比值R，产生了不同的抓取模式，如图4所示。现就具体情况进行讨论[15]。

图4 不同抓取模式的转换Fig.4 Bifurcations between various grasp types

对于五点接触，目标物与手掌、近端指节和远端指节同时接触。当R到达五点接触的上限值R5,max时，近端指节的接触力趋近于零，令式(8)中接触力F1=0可得：

(19)

当R到达五点接触的下限值R5,min时，目标物与手掌之间的接触力趋近于零。随着R的减小，接触状态将向四点接触转换。令式(7)中Fpalm=0并代入式(8)中得到:

R5,min=

(20)

对于四点接触，目标物与近端指节、远端指节同时接触，且与手掌不发生接触。当R到达四点接触的上限值时，物体与手掌处于临界接触状态，与R5,min的状态一样，因此有:

R4,max=R5,minL1≤L0+L2

(21)

当L1>L0+L2时，将会造成四点接触下的抓取失稳。

当R到达四点接触的下限值R4,min时，远端指节趋近于竖直状态，有θ1+θ2=π/2。随着R的减小，接触状态将向两点接触转换。由式(7)和式(8)可得:

(22)

当三点接触达到上限值时，目标物与远端指节、手掌接触，与近端指节不发生接触。将F1=0代入式(8)可得:

(23)

若R继续增大，将会造成三点接触下的抓取失稳。

当三点接触到达其下限R3,min时，目标物与近端指节、手掌都处于临界接触状态。随着R的减小，根据目标物的不同半径，其接触状态将向五点或两点接触转换。当robjrobj,5时，其转换为两点接触，因此根据式(10)和式(11)可得：

(24)

两点接触时，目标物只与远端指节接触，此时F1=0，因此式(23)仍然成立。当R达到两点接触的上限R2,max时，接触点位于远端指节的顶端，即p2=L2，此时有:

(25)

当R到达两点接触的下限R2,min时，目标物与近端指节、手掌都处于临界接触状态。由于一般情况下两点接触很难实现抓取稳定，因此其最终可能转换为三点或四点接触以实现稳定抓取，或最终抓取失败。因此有:

(26)

通过以上对不同抓取模式拓扑转换的定量分析可知，在目标物尺寸已知的情况下，基于不同弹簧扭矩与驱动力矩之间的比值R，由式(9)可获取弹簧刚度的适用范围。

3 不同抓取模式下平衡与接触轨迹分析

当欠驱动指爪抓取目标物达到稳定后，目标物与远端指节的平衡位置e也随之固定。对于不同的接触状态，平衡轨迹的表达也不同。在上面已经讨论过，两点接触为临界稳定状态，难以实现稳定抓取，因此下面不再赘述。

五点接触下的几何关系如图3所示,由三角形全等关系(ΔOC0O1≅ΔOC1O1和ΔOC1O2≅ΔOC2O2)可得：

p2=e=L1-L0

(27)

当四点接触时，物体与手掌脱离。将Fpalm=0和式(3)代入式(7)可得平衡轨迹：

p2=e=

(28)

式中：T3=Ta-Kθ1。

当三点接触时，物体只与远端指节接触，因此有F1=0, 代入式(3)可得平衡轨迹:

p2=e=

(29)

此外，在欠驱动指爪抓取目标物的过程中，接触点会在远端指节上相对滑动，直到抓取稳定或失败。如图2(b)所示，O1、O2与接触点形成一个三角形，若目标物位置不发生变化，欠驱动指爪最终达到稳定位形，则由几何关系可得:

(30)

其中，接触轨迹可确定在(p2,θ2)坐标平面内，即“抓取状态平面”。据此，可获得不同抓取模式下稳定抓取的定量条件，即接触轨迹与平衡轨迹的重合部分是实现稳定抓取的先决条件。

4 弹簧刚度的优化设计

4.1 弹簧刚度的取值范围求解

为了方便弹簧刚度的优化，给定一个各连杆长度已知的欠驱动指爪(L1=40 mm、L2=50 mm和L0=20 mm)和腱线拉力Fm=10 N。根据不同抓取模式下R和目标物半径的关系表达式(19)～式(24)，对于特定的Rmax与Rmin，分析弹簧刚度与静摩擦系数以及目标物半径之间的关系，如图5所示。

图5 刚度与静摩擦系数、目标物半径之间的关系Fig.5 Relationship between K, μ and robj

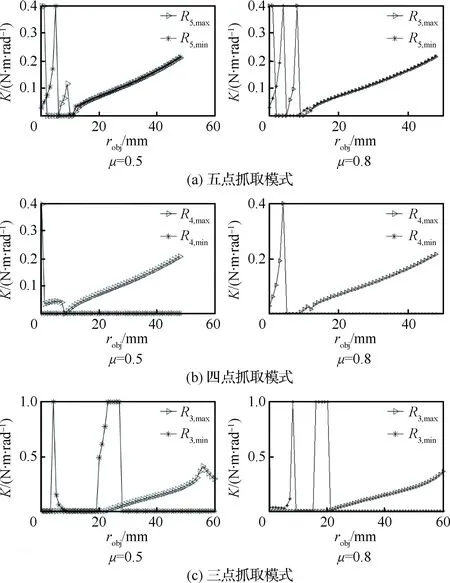
图6 不同摩擦系数下刚度与目标物半径之间关系Fig.6 Relationship between K and robj in different μ

从图5中可看出摩擦系数与目标物半径对弹簧刚度的影响。一般情况下，当目标物材质确定后，手指与目标物之间的摩擦系数也随之确定。给定摩擦系数μ=0.5和μ=0.8，不同抓取模式下刚度与目标物半径之间的关系如图6所示。从图中可以看出，若弹簧刚度固定，欠驱动指爪可抓取一定尺寸范围内的目标物；若目标物半径已知，可得该半径下Rmax与Rmin之间所对应的刚度范围。如图6所示，当μ=0.5时，对半径为30 mm的目标物，三点接触下刚度范围为0～0.055 N·m/rad，四点接触下刚度范围为0～0.113 N·m/rad，五点接触下刚度范围为0.112～0.113 N·m/rad。

4.2 基于抓取状态平面的弹簧刚度与稳定区域关系

图7 不同接触状态下的平衡轨迹图Fig.7 Curves of equilibrium in various grasp types

根据不同接触状态下平衡轨迹的表达式式(27)～式(29)，得到平衡轨迹的3D图形，如图7所示。纵坐标为远端指节平衡位置e与其杆长L2的比值，横坐标为弹簧刚度K与远端指节和近端指节之间的夹角θ2。从7(a)中可看出五点接触只与欠驱动指爪的几何参数L0和L1有关，与摩擦系数和弹簧刚度无关。因此，在该接触状态下，弹簧刚度不会对抓取稳定性造成影响。在四点与三点接触下，平衡轨迹的3D图形如图7(b)和图7(c)所示，从图中可以看出，该平衡轨迹不但与弹簧刚度K和转角θ有关，还与静摩擦系数μ有关。

因此，将μ=0.5得到的平衡轨迹与式(30)结合，得到四点与三点接触下不同弹簧刚度的稳定区域，如图8和图9所示。其中,θik(k=1,2,3)代表角度θ2的一系列变化值，θi1为平衡轨迹与几何约束(p2=0)的交点，θi2为平衡轨迹与接触轨迹的交点，θi3为接触轨迹与几何约束(p2=L2)的交点。当接触点在白色区域时，F1会在关节处产生扭矩，使得接触点向靠近平衡轨迹的方向移动，最终和平衡轨迹相交，抓取达到稳定，因此称白色区域为稳定区域。但并不是两者相交就能达到稳定，如图8(b)中(1)区域，接触轨迹与平衡轨迹左半部分有交点，但其与右半部分相交前就已到达限位。另一种情况如8(a)中(2)区域所示，接触点在该区域时接触力F1<0,因此在关节1处产生逆时针的扭矩，使得接触点沿着背离平衡轨迹的方向运动，如图中该区域箭头所指方向。

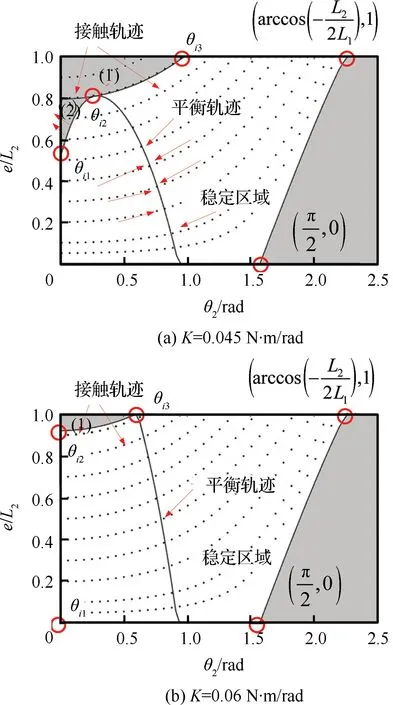
图8 四点接触状态下的稳定区域Fig.8 Stability regions of 4-point grasp type

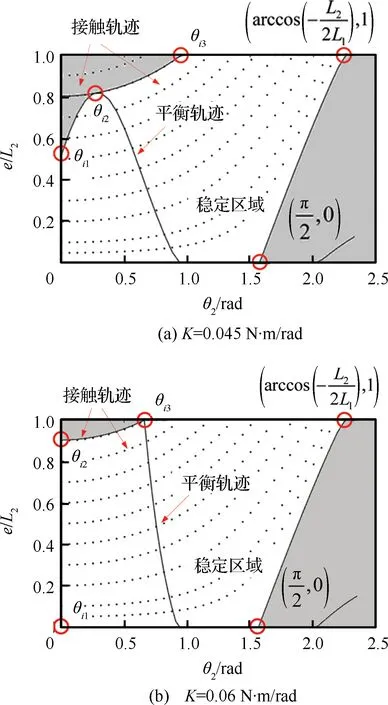
图9 三点接触状态下的稳定区域Fig.9 Stability regions of 3-point grasp type

通过积分计算图中白色稳定区域的面积：

(31)

式中：g(θ2i)为抓取状态平面上θi2和θi3之间的接触轨迹片段，其表达式为

(32)

f(θ2i)为抓取状态平面上θi2和θi3之间的平衡轨迹片段，表达式为

(33)

式中：cF3=cF1+cF2。

综上所述，对于不同半径的目标物，由式(31)得到三点与四点接触时弹簧刚度与机构稳定区域的关系，如图10所示。从图中可以看出，当弹簧刚度增大时稳定区域面积也随之增大；当弹簧刚度增大到某一值时，稳定区域的面积达到最大；其后随着弹簧刚度的增大，稳定区域面积基本不变。

由图10(b)可知，对于μ=0.5和robj=30 mm的抓取状态模型，当弹簧刚度增大到0.055 N·m/rad时，三点与四点接触的稳定区域面积都达到最大。同时，刚度0.055 N·m/rad也在三点与四点接触可选择的刚度范围内。因此， 该模型的最优弹簧刚度为0.05 N·m/rad。为了进一步验证本文方法的适用性，分别建立不同摩擦系数与目标物半径的抓取状态模型，通过优化设计得到其最优弹簧刚度，如表1所示。

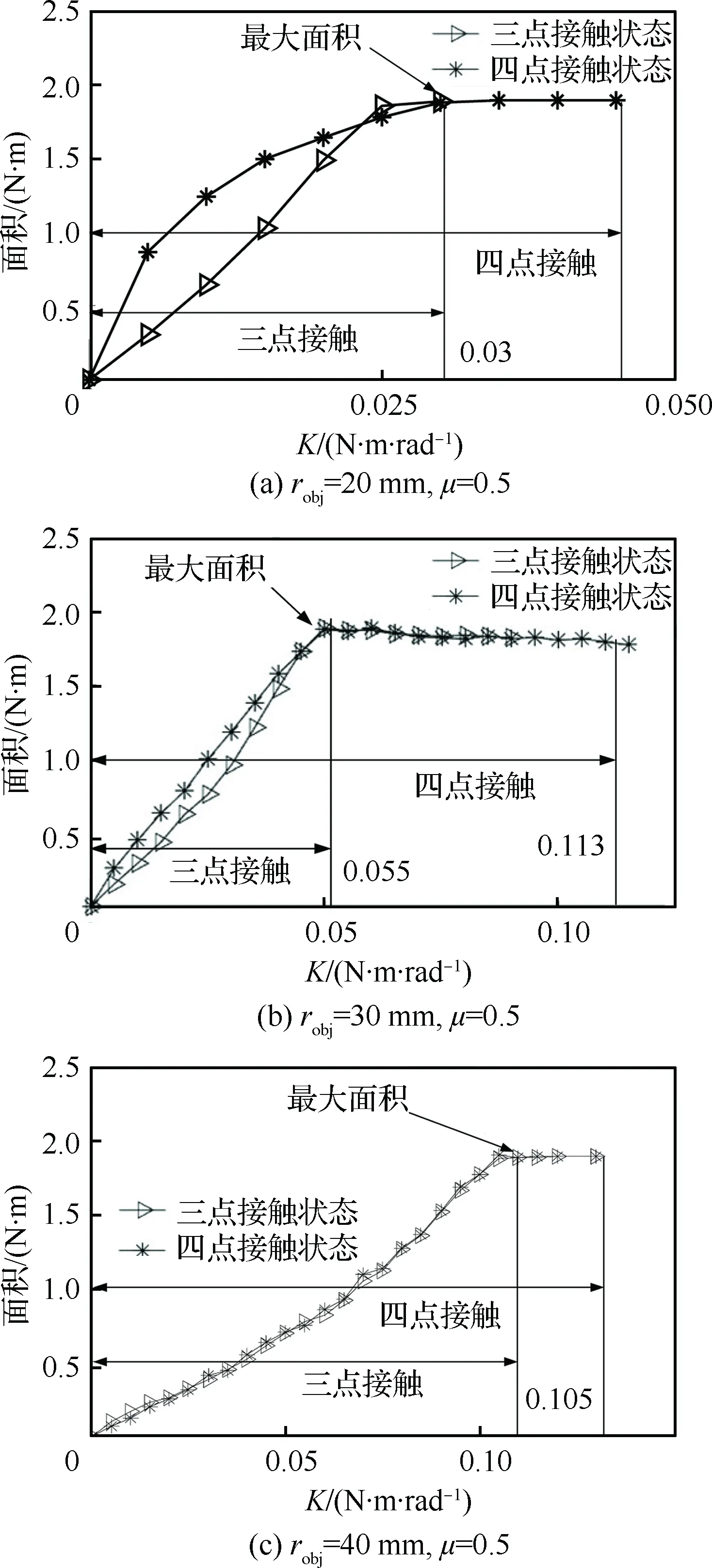
图10 弹簧刚度优化Fig.10 Spring stiffness optimization

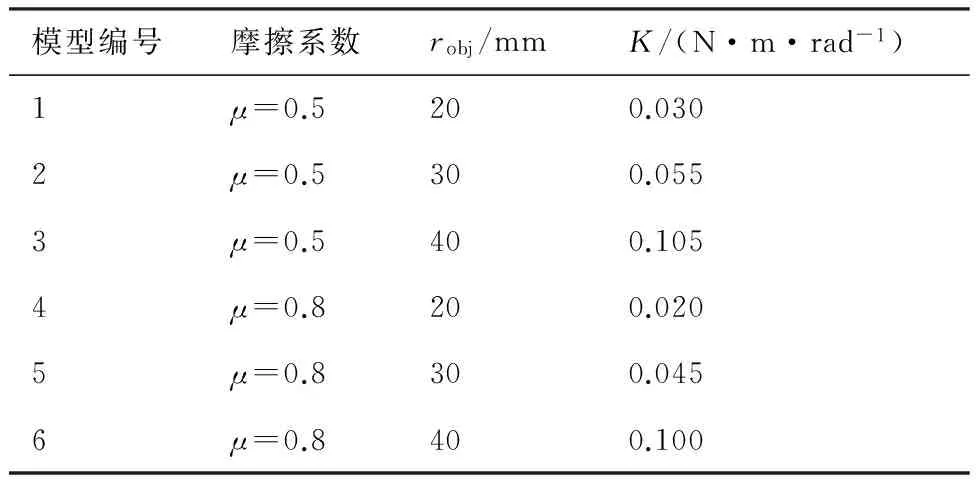
表1 最优弹簧刚度Table 1 Optimal spring stiffness

5 结 论

1) 提出一种欠驱动指爪被动弹性元件参数的优化设计方法，将弹簧刚度作为设计参数，以实现欠驱动指爪抓取稳定性与自适应能力之间的平衡。

2) 通过对欠驱动指爪力传递关系的静力学分析，建立弹簧刚度与驱动力的平衡方程，完成欠驱动指爪在不同抓取模式下拓扑转换的定量分析。

3) 在抓取状态平面法的基础上，建立弹簧刚度与机构稳定区域关系的解析表达，并基于稳定区域面积最大化的思想，进行最优弹簧刚度的设计。最后，通过不同抓取状态模型的仿真设计，验证了本文方法的有效性与适用性。

欠驱动指爪的自适应抓取源于机构的欠驱动特性，而对于欠驱动指爪，抓取稳定性是其重要研究内容之一。因此，在下一步工作中，将对欠驱动指爪进行稳定性分析，并验证所提出的弹性元件参数优化方法对不同刚度目标物的自适应抓取能力。

[1] DOLLAR A M. Analyzing dexterous hands using a parallel robots framework[J]. Autonomous Robots, 2014, 36(1-2): 169-180.

[2] MASON M T, RODRIGUEZ A, SRINIVASA S S, et al. Autonomous manipulation with a general-purpose simple hand[J]. International Journal of Robotics Research, 2012, 31(31):688-703.

[3] CARROZZA M C, SUPPO C, SEBASTIANI F, et al. The SPRING hand: development of a self-adaptive prosthesis for restoring natural grasping[J]. Autonomous Robots, 2004, 16: 125-141.

[4] WU L C, CARBONE G, CECCARELLI M. A numerical simulation for design and operation of an underactuated finger mechanism for LARM hand[J]. Mechanics Based Design of Structures and Machines, 2009, 37(1): 86-112.

[5] CABAS R, CABAS L M, BALAGUER C. Optimized design of the underactuated robotic hand[C]∥2006 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2006: 982-987.

[6] WU L C, CARBONE G, CECCARELLI M. Designing an underactuated mechanism for a 1 active DOF finger operation[J]. Mechanism & Machine Theory, 2009, 44(2):336-348.

[7] ZHANG W, CHEN Q, SUN Z, et al. Passive adaptive grasp multi-fingered humanoid robot hand with high under-actuated function[C]∥2004 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2004: 2216-2221.

[8] ODHNER L U, JENTOFT L P, CLAFFEE M R, et al. A compliant, underactuated hand for robust manipulation[J]. International Journal of Robotics Research, 2014, 33(5): 736-752.

[9] AUKES D M, HEYNEMAN B, ULMEN J, et al. Design and testing of a selectively compliant underactuated hand[J]. International Journal of Robotics Research, 2014, 33(5): 721-735.

[10] ODHNER L U, DOLLAR A M. Stable, open-loop precision manipulation with underactuated hands[J]. International Journal of Robotics Research, 2015, 34(11): 1347-1360.

[11] KRAGTEN G A, HELM F C T V D, HERDER J L. A planar geometric design approach for a large grasp range in underactuated hands[J]. Mechanism & Machine Theory, 2011, 46(8): 1121-1136.

[12] PRATTICHIZZO D, MALVEZZI M, GABICCINI M, et al. On the manipulability ellipsoids of underactuated robotic hands with compliance[J]. Robotics & Autonomous Systems, 2012, 60(3): 337-346.

[13] DOLLA A M, HOWE R D. The highly adaptive SDM hand: Design and performance evaluation[J]. International Journal of Robotics Research, 2010, 29(5): 585-597.

[14] BIRGLEN L, LALIBERTE T, GOSSELIN C. Underactuated robotic hands[J]. Berlin: Springer Berlin, 2008: 40.

[15] KRUT S, BEGOC V, PIERROT F, et al. Extension of the form-closure property to underactuated hands[J]. IEEE Transactions on Robotics, 2010, 26(5): 853-866.

[16] 楚中毅, 周苗, 胡健, 等. 主被动复合驱动自适应指爪机构的抓取模式分析[J]. 航空学报, 2014, 35(12): 3451-3458.

CHU Z Y, ZHOU M,HU J, et al. Gripping mode analysis of an active-passive composited driving self-adaptive gripper mechanism [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3451-3458(in Chinese).

[17] JUNG G P, KOH J S, CHO K J. Underactuated adaptive gripper using flexural buckling[J]. IEEE Transactions on Robotics, 2013, 29(6): 1396-1407.

[18] ODHNER L U, DOLLAR A M. Dexterous manipulation with underactuated elastic hands[C]∥2011 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2011: 5254-5260.

[19] 刘菲, 何广平, 陆震. 弹性欠驱动四指灵巧手设计与试验[J]. 机械工程学报, 2014, 50(15):53-59.

LIU F, HE G P, LU Z. Research anddesign of a novel tendon driven underactuated multi-fingered hand[J]. Journal of Mechanical Engineering, 2014,50(15): 53-59 (in Chinese).

[20] KO H K, CHO C H, KWON H C, et al. Design of an underactuated robot hand based on displacement-force conversion mechanism[J]. International Journal of Precision Engineering and Manufacturing, 2012, 13(4): 509-516.