级联式储能电池组均衡器及其自均衡策略

陈 威 叶少士 刘 冬

作为清洁能源技术在智慧城市中的重要组成应用，分布式微电网的建设和发展一直是国内外研究的重要课题，并在我国已经列入了“十三五”规划。其中，储能系统又是微电网系统发展中的重点，特别是作为储能系统基本单元的串联电池组的性能优劣，直接决定了整体系统的可靠性和安全性，堪称是新能源技术能否有效普及的关键因素[1-2]。储能系统电池组性能提升的瓶颈在于：通过各种均衡电路和控制手段，在充放电过程中尽量消除因各电池单体之间性能差异，从而发挥储能系统最大用容量和整体装置可用率[3-11]。同时城市环境下的狭小空间和高密度分布的特点，又对储能系统提出了简单高效体积小的要求。近年来，属于节能环保的有源平衡型电池组均衡器取得了长足发展。根据均衡电路所采用的原理不同，有源平衡型均衡器可分为开关电容/电感型和DC-DC变流器型两种形式[3-7]。一般而言，采用能量双向流动的DC-DC变流器或反激式变流器，配合电池的荷电状态(state of charge, SOC)检测，可有效地将能量由电池组中端电压或SOC最高的单体电池向最低的单体电池转移，以达到均衡[9]。但要准确而可靠地获得电池的 SOC，需附加一系列电池单体传感器外围电路和高性能微处理器，从而增加了系统复杂度和整体装置体积成本[10]，且受限于城市空间的实际使用特点，该技术不利于大面积推广。并且电池组的SOC估计又与均衡控制策略密切相关，不同的均衡控制策略导致不同的单体最终状态特性，反过来又直接影响电池组SOC的估计[11]。另外，DC-DC变流器的使用也增加了系统额外效率损耗，影响热设计和功率密度的提升[7]。

本文提出了一种新颖的非隔离开关电感式级联电池组均衡器。该均衡器利用简单的开关管和电感的组合，即可实现能量的双向流动，而无需复杂的双向变流器辅助。同时，采用的自均衡控制策略可自动平衡每一个电池单体的电压，无需采集电池单体参数信息，舍弃了实现复杂控制算法的微处理器和外围传感器电路。因而该简单低成本的均衡器非常适合应用于在城市环境下的分布式微电网的储能系统中。在给出原理分析的参数设计后，一台实际样机证明该均衡器和自主均衡策略的有效性。

1 均衡器电路结构和工作原理

级联式电池组均衡模块电路如图1所示。每一节电池对应一个均衡模块，该均衡模块通过 4个MOSFET开关管和一个均衡电感组成H桥，连接至公共均衡电容CB上。电池组中的任意一节电池均可以通过均衡电路模块和CB进行能量的双向传递，所有的均衡模块组成级联形式。等效电路如图2所示，当电池电压VB大于电容电压bCV 时，能量由电池传递至 CB；反之，则能量从 CB回充至电池。因此，若将电池组中的相邻电池依次逐一比较，则强电池的能量经过 CB的中转和收敛，会逐步传递给弱电池，最后达到所有单体之间的互相平衡。图3和图4给出了该均衡电路在两个模块均衡的具体工作过程。为了保证n位的均衡模块不影响n+1位均衡模块的正常工作，需要将 n位均衡电感设置工作在DCM模式，即要将n位均衡模块的开关管占空比设为不大于0.5。另外对于不同的电池单体，需要分奇偶序数分别开通对应的开关管。下面分别加以分析。

1.1 奇序数电池的能量传递

如图3所示，在时刻t0时，由开关管S11、S13、S21和 S24导通，B1、L1、L2和 CB组成通路。此时L1和L2中的电流iL大小可由下式表示：

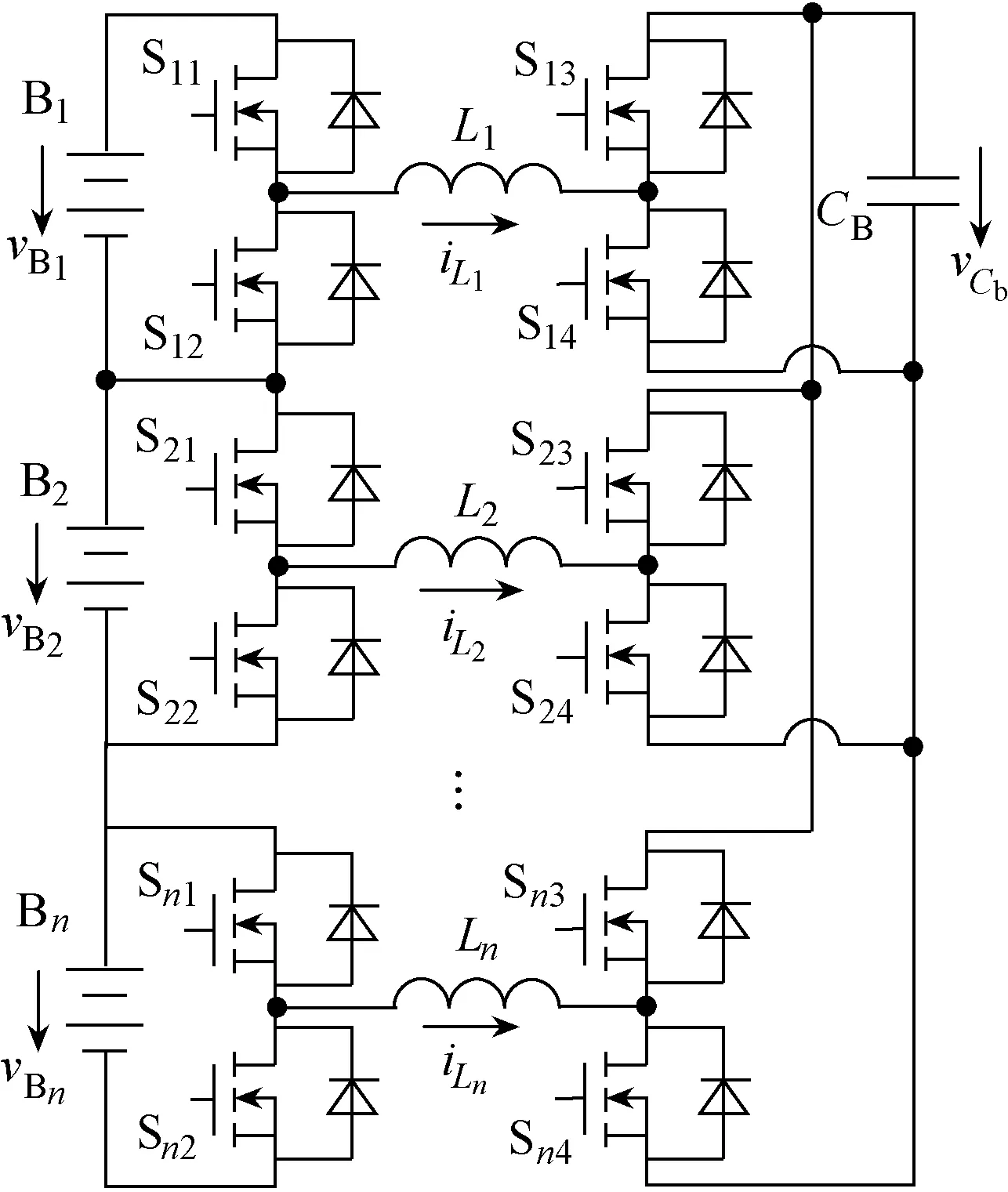
图1 级联式电池组均衡模块电路

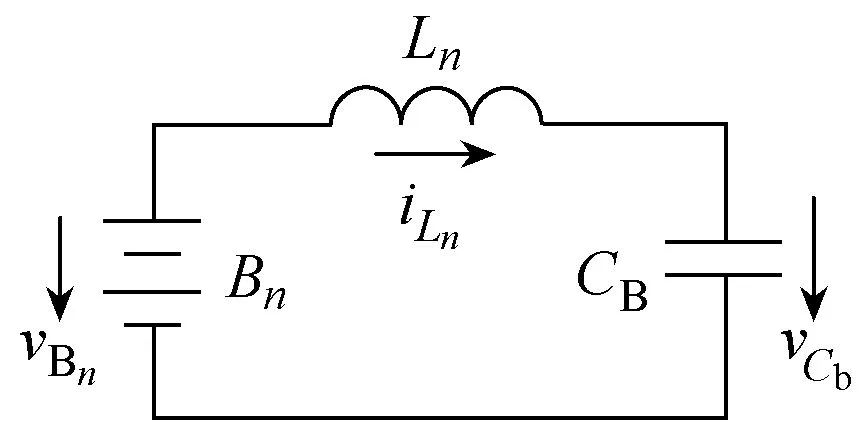
图2 均衡模块等效电路

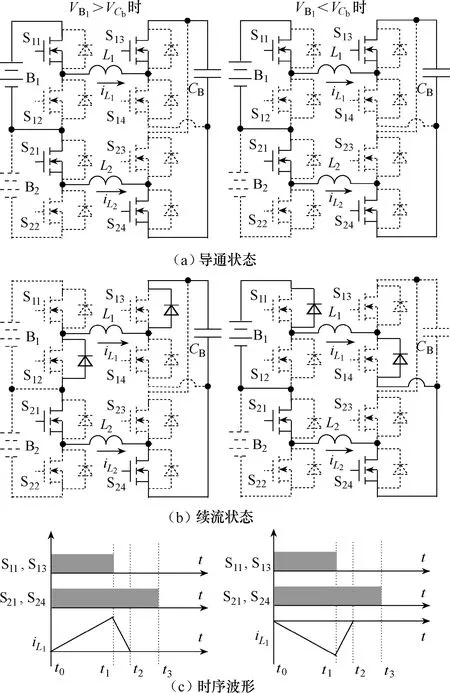
图3 奇序数时的能量传递过程

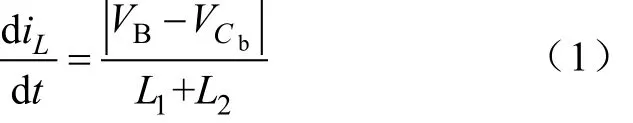
在时刻 t1、iL达到峰值，此时开关管 S11和 S13关断，但 S21和 S24仍保持导通，iL经过均衡模块 1中开关管的体二极管续流，具体的通路需根据 VB1和bCV 的值而定。当1BV 大于bCV 时，iL经S12和S13的体二极管续流；反之，则经过S11和S14的体二极管。此时iL的大小可由下式表示：

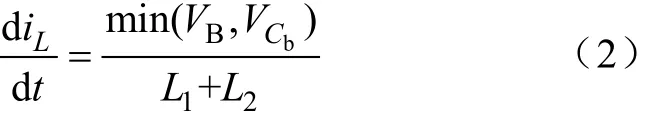
在时刻 t2、iL的电流下降到零，S21和 S24无需关断，不影响电路状态。一直到时刻 t3，一个周期结束，S21关断，电路进入偶序数电池的能量传递状态。

1.2 偶序数电池的能量传递

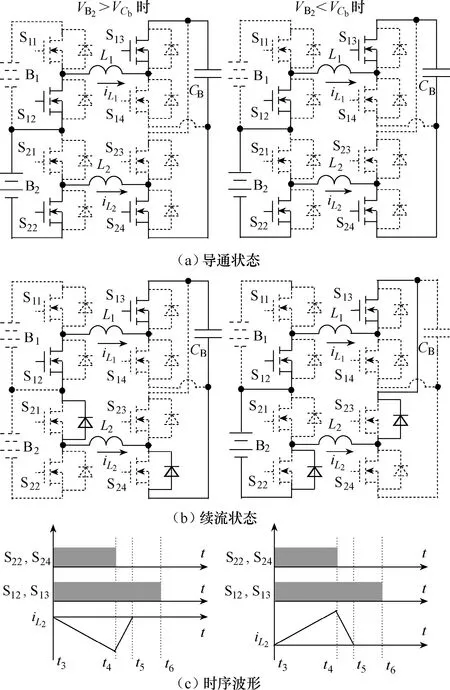
图4 偶序数时的能量传递过程

如图4所示，在时刻t3时，由开关管S12、S13、S22和 S24导通，B2、L1、L2和 CB组成通路。此时L1和L2中的电流iL大小仍如式（1）所示。

在时刻 t4、iL达到峰值，此时开关管 S21和 S24关断，但 S12和 S13仍保持导通，iL经过均衡模块 2中开关管的体二极管续流，具体的通路需根据2BV和bCV 的值而定。当2BV 大于bCV 时，iL经S21和S24的体二极管；反之，则经过S22和S23的体二极管。此时iL的大小仍如式（2）所示。

在时刻 t5、iL的电流下降到零，S12和 S13无需关断，不影响电路状态。一直到时刻 t6，一个周期结束，S12关断，电路进入奇序数电池的能量传递状态。

在上述工作过程中，所有开关管均选用MOSFET，且工作在饱和区，导通压降可以忽略，即电池和CB之间因半导体器件带来的电压差可以忽略，两者之间可以无限逼近。由此可见，若经过电池组所有单体电池和CB之间能量转移交换的循环遍历，则最终可以达到单体电池之间互为相等的均衡状态。该自均衡过程是完全自发，无需借助外部传感电路和复杂算法，因而使整体设计大为简化。

2 参数设计

2.1 电池组单体最终均衡电压的讨论

基于上述原理，在最终均衡状态时，电池组内单体电池的电压即等于公共电容CB的最终电压。但该最终电压不能简单理解为所有单体电池初始端压代数和的平均。由于自均衡的过程实质是系统存储电量的再分配过程，因此CB在自均衡过程中电压的变化量才反映了各个电池之间电量重新分配的守恒，即需要满足下式：

式中，bCVΔ是CB在均衡前后的电压变化量；ΔQB为电池单体在均衡前后的电量变化量；m表示电量净流出的电池数；n表示电量净流入的电池数。然后根据CB在初始状态下的电压即可求出终态电压。但因为要保证均衡电路的正常工作，即均衡电感电流在一周期内必须归零，显见 CB的初始值不能太小，一般对于锂离子电池单体，取标称值3.6V的预充初始电压是合适的。

2.2 均衡电感和均衡电容的设计

均衡电感是连接电池单体和均衡电容能量转换的桥梁，在均衡器中占据核心位置。如上文分析所述，为了保证均衡器的正常工作，在每一周期内均衡电感电流iL必须要回归至零，即需要工作在DCM模式。假设所有均衡电感的感量一致为 L，则在一个周期内iL的峰值可以表述为

式中，IL_pk为均衡电感的峰值电流；ΔV是当前单体电池端压和公共均衡电容CB电压之差；Ton为当前n均衡模块中的开关管的导通时间。

由电感伏秒积平衡，由式（2）和式（4），易得均衡电感中电流从峰值下降到零所需时间TL_off为

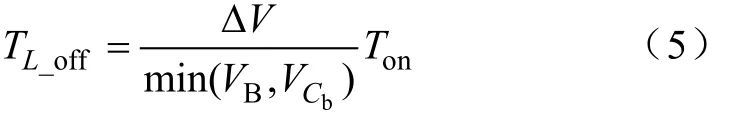
设单体均衡模块一个开关周期时间为TS，则要保证均衡电感工作在 DCM，必须要满足 TL_off≤TS-Ton，即有

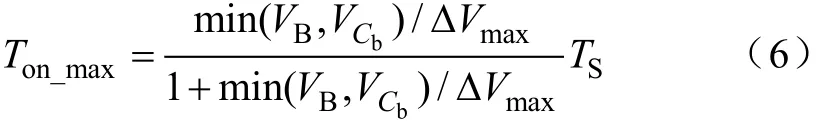
式中，ΔVmax是电池组中偏差最大的两个电池单体之间的极差。由式（6）可见，电池组之间的差异越大，Ton时间就需要越小，以保证均衡电感可以工作在DCM模式。但是在实际应用中，电池组之间的极差很小，一般为几十至几百毫伏，因此，Ton时间最大值可以取值在一半的开关周期。

由式（4）和式（6）可得均衡电感的平均电流为

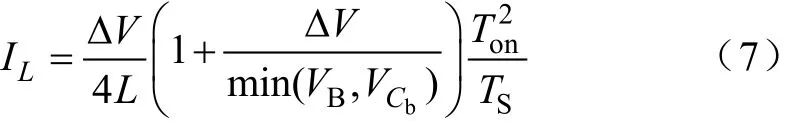
可见到达最终均衡状态时，因ΔV=0，故电感电流为零，即表示均衡模块能量流动停止。此时若电池组处于静置不工作状态，即可停止开关管的工作，以达到静态损耗的最小化。

对于公共均衡电容CB，为了达到整体系统的快速均衡收敛，其容量应远小于电池单体的储能容量。但电容取值的下限又受制于电容一个周期内充放电时的纹波大小，该纹波需要远小于电池单体端压和电容电压的偏差ΔV，以保证能量均衡的顺利完成，即有Vripple＜＜ΔV。可得下式：

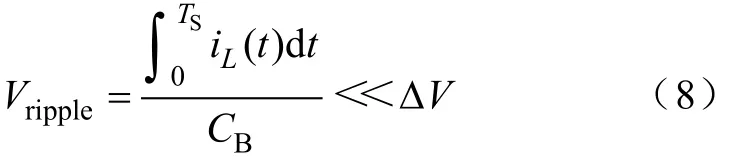
结合式（5）至式（7），继而可得

3 实验波形

为了验证本文所提方法的有效性，首先构建了一套由两个电池单体组成的电池组样机，并加以按图1所示的均衡电路。为了能够用示波器抓取关键波形，该样机的电池组单体用大电容的方式模拟以加快均衡进程，方便示波器读取细节。该样机的参数见表1。

表1 主要器件参数

图5给出了该均衡电路的实际运行效果。其中用电解电容模拟的 VB1和 VB2分别被预充至 6V和4V，CB上的电压被预充至5V，为B1和B2预充电压代数和的一半。可以看到，在该基本无损的系统中，最终均衡电压即保持在约5V左右，且和CB的终值电压相等，即ΔV=0。可见 B1中的高电量已转移至B2的低电量中去，两者的能量得以平均，符合式（3）。同时均衡电感中的电流只是在均衡过程中存在，待系统均衡完毕后即降为零，减少了系统的静态损耗。图6是在均衡过程中，将图5中的均衡电感电流加以时间放大。在满足式（6）和式（9）的条件下，均衡电感内的电流在每一周期内可下降至零，即保证了 DCM 的工作状态，均衡电路模块之间不产生互相干扰，使系统正常运行。

为了验证该均衡电路的实际运行效果，同时还搭建了实际的电池组充电平台，该平台由已被放电至截止电压的4节电池组成。在加以本文所提的均衡电路后，对该平台进行充电并记录读数，以其中的一节电池达到充电截止电压作为结束时间点。比较均衡电路施加前后的电池一致性。实验结果如图7及表2所示。

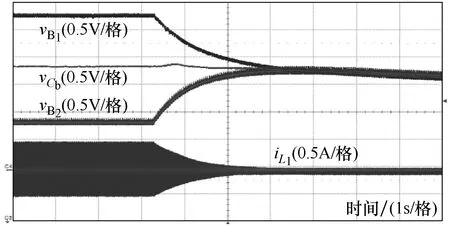
图5 均衡器验证样机的实际均衡效果

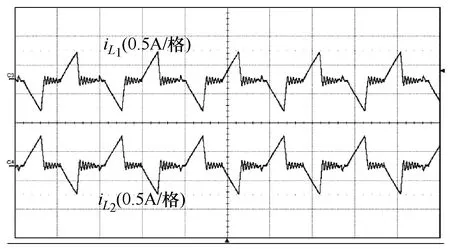
图6 均衡过程中L1和L2的电流波形

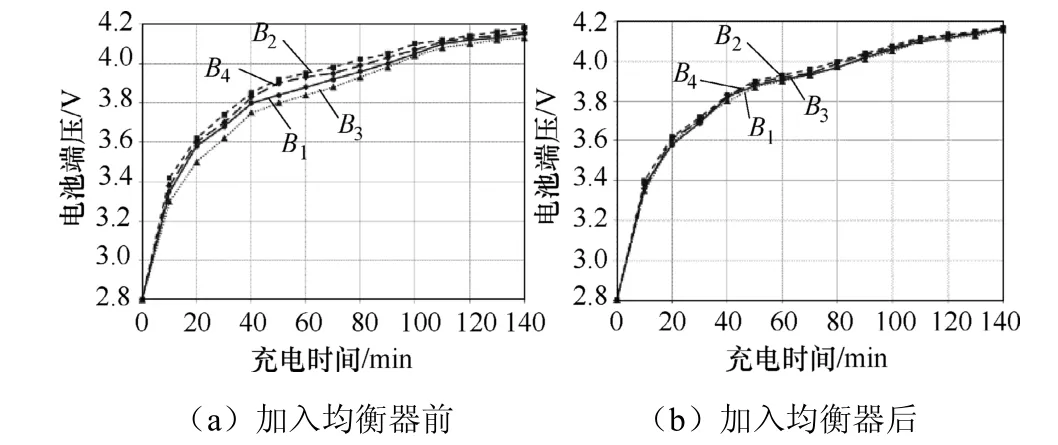
图7 均衡器在电池组实际充电时的均衡效果

表2 加入均衡电路前后对比

从图7和表2可知，在未施加均衡电路前，充电完毕时电池组电压较为不均，电压极差达到了50mV左右。在施加了均衡电路后，极差可减小至15mV左右，显著改善了电池组的整体一致性，减小了因单体电池差异带来的短板效果，延长了装置的使用寿命。

4 结论

本文提出一种新颖非隔离开关电感式级联电池组均衡器。该均衡器电路通过简单的电路构造，即可在电池组单体和一个公共电容之间实现能量的无损双向流动，进而在电池单体之间互相遍历，最终即可达到整体状态均衡。控制方式简单，无需电池单体外围传感器和微处理器，极大地降低了成本，具有经济优势。搭建的验证样机和电池组充电平台均验证了该均衡器的有效性，具有在城市环境下分布式微电网储能系统中应用的实际工程推广价值。

[1] 周林, 黄勇, 郭珂. 微电网储能技术研究综述[J]. 电力系统保护与控制, 2011, 39(7)： 147-152.

[2] 戴咏夏. 电动汽车动力电池运维精益化管理探索与实践[J]. 电气技术, 2016, 17(3)： 120-122.

[3] Baughman A C, Ferdowsi M. Double-tiered switchedcapacitorbattery charge equalization technique[J].IEEE Transactions on Industial Electronics, 2008,55(6)： 2277-2285.

[4] 张涛, 朱小平. 基于 LLC变换器的电动汽车充电机设计[J]. 电气技术, 2016, 17(6)： 97-100.

[5] Mestrallet F, Kerachev L, Crebier J C, et al.Multiphase interleaved converter for lithium battery active balancing[J]. IEEE Transactions on Power Electronics, 2014, 29(6)： 2874-2881.

[6] 韩腾飞, 杨明发. 基于双模 MPPT控制的光伏充电设计[J]. 电气技术, 2017, 18(4)： 49-55.

[7] 刘红锐, 张昭怀. 锂离子电池组充放电均衡器及均衡策略[J]. 电工技术学报, 2015, 30(8)： 186-192.

[8] 吕航, 刘承志, 尹栋, 等. 深海动力磷酸铁锂电池组均衡方案设计优化[J]. 电工技术学报, 2016, 31(19)：232-239.

[9] 艾洪克, 吴俊勇, 郝亮亮, 等. 级联式储能系统中电池自均衡控制策略研究[J]. 电工技术学报, 2015,30(14)： 442-449.

[10] 王琪, 孙玉坤, 倪福银, 等. 一种混合动力电动汽车电池荷电状态预测的新方法[J]. 电工技术学报,2016, 31(9)： 189-196.

[11] 冯飞, 宋凯, 逯仁贵, 等. 磷酸铁锂电池组均衡控制策略及荷电状态估计算法[J]. 电工技术学报, 2015,30(1)： 22-29.