基于CFD的FSAE赛车尾翼设计及优化研究
俞凯南,谢世滨
(1.浙江工业大学 机械工程学院,浙江 杭州 310006;2.浙江吉利汽车研究院有限公司,浙江 杭州 310000)
0 引 言
近年来,随着中国大学生方程式汽车大赛(FSC、FSEC)在中国迅速发展,各高校开始将更多的精力投入到空气动力学的研究中。当赛车与空气发生相对运动时,空气会对赛车产生气动力和气动力矩,因此赛车空气动力学对于赛车的动力性能、操控性能都有着重要的影响[1-2]。研究表明,当作用在轮胎上的垂直载荷增加时,轮胎的侧偏刚度也会增加[3],因此轮胎在到达相同的侧偏角时可以承受更大的侧向力,提高车辆的侧向加速度,增加过弯速度。方程式赛车可以通过添加负升力翼的方式来利用空气产生下压力,从而增加作用在轮胎上的垂直载荷[4]。
对于方程式赛车,能够提高的赛车下压力的空气动力学套件主要有负升力翼、扩散器等,其中负升力翼根据安装位置不同分为前翼和尾翼,其中翼型的参数和翼片组合是负升力翼能否有效工作的关键。文献[5]对NACA4412翼型原型以及改变修型开始位置、尾缘厚度、光滑曲线形状等6种改型进行了数值模拟计算,发现改型在一定迎角范围内能有效提高翼型的升力系数和升阻比;文献[6]对FSAE赛车的尾翼进行了研究,分别对不同翼型组合、翼片攻角、离地高度、翼片数量进行了CFD分析对比,结果表明曲率较大、翼身较厚的翼型会产生较大的升力;文献[7]分别对赛车尾翼的不同翼型组合进行了数值模拟计算,发现增加尾翼襟翼的弯度和攻角有助于提升尾翼的升力系数。
本研究对某FSAE赛车的尾翼进行设计和CFD仿真分析。
1 FSAE赛车尾翼翼型设计和优化
FSAE赛车的尾翼的负升力完全是负升力翼产生的,不同的负升力翼将会产生不同的气动效果。FSAE赛车尾翼的翼型通常为倒置的航空翼型,通过气流通过翼型上下表面速度不同而产生压力差,从而产生负升力。与航空翼型不同的是,FSAE赛车的运动速度较慢,即:
(1)
式中:ρ—流体密度;V—流体速度;d—特征长度;μ—动力黏度。
其负升力翼周围的雷诺数也比较低,因此不能简单地将航空翼型倒置,而需根据FSAE赛车的特点进行设计。翼型是赛车尾翼气动性能的最关键部分,翼型的负升力系数、升阻比等气动特性通常跟其攻角、最大弯度及最大弯度所在位置有关[8]。研究表明,翼型在攻角为0的时候,其负升力系数可能为0也可能不为0。但当翼型攻角增加时,其负升力系数随之增加,两者呈线性关系。当翼型攻角增加至一定程度时,翼型下表面的气流会因逆压梯度过大产生气流分离,此时翼型攻角和翼型负升力系数的关系已不再是线性,但翼型负升力系数仍随着翼型攻角的增加而增加。当翼型攻角继续增加时,翼型的气流分离愈发严重,存在一个临界攻角,在此攻角下,翼型负升力系数达到最大值,若继续增加翼型攻角,翼型就将发生失速现象。
1.1 控制方程和湍流模型
1.1.1 控制方程
流体流动时必须遵守质量守恒定律、动量守恒定律和能量守恒定律。由于FSAE赛车行驶时的马赫数远小于0.3,在对FSAE赛车进行流场仿真时,赛车周围的空气视为不可压缩气体,且空气的黏性系数为常数。根据质量守恒定律可以推导出连续性方程:
(2)
式中:u,v,w—流体在点(x,y,z)处的速度分量。
根据质量守恒定律、动量守恒定律和能量守恒定律可以导出纳维-斯托克斯方程(Navier-Stokes equations):

(3)
式中:v—速度矢量;F—单位质量的质量力;μ—动力黏度。
式(2)和式(3)一起构成了不可压缩流体运动基本方程组。该方程组为非线性偏微分方程,除在一些特定条件下,很难得到精确解,因此本研究采用CFD的方法进行数值计算。
1.1.2 湍流模型
本研究选择Realizablek-ε湍流模型作为数值模拟湍流流动的湍流模型。Realizablek-ε模型是标准k-ε模型的修正式,Realizablek-ε模型中,湍动能k和湍动耗散率ε的输运方程为:
(4)
(5)
其中:

Realizablek-ε模型与标准k-ε、RNGk-ε模型不同的是,其涡粘度为:
(6)
同时,式(6)中Cμ的不再是一个常数,它通过下式计算得出:
(7)
因此,Realizablek-ε模型可以保持雷诺应力与真实湍流一致,可以更精确地模拟平面和射流的扩散速度。同时在旋流计算、带方向梯度压强的边界计算和分离计算中,计算结果也更符合真实结果。
1.2 翼型CFD分析网格与边界条件
首先本研究需要对流场确定计算域,计算域一般取长方体以此来模拟风洞实验。对翼型进行自由流场CFD分析[9],研究人员可将计算域尺寸设置稍小一些,以提高计算效率。对计算域划分网格来到达将流场离散化的目的。由于负升力翼的对称性,研究人员可以根据对称性仅对一半的计算域进行网格划分,提高计算效率。使用非结构网格来捕捉翼片的几何特征,并在翼片表面划分附面层网格从而模拟翼片的边界层效应。在气流压力梯度变化剧烈的区域减小网格尺寸以提高计算精度,在气流压力提低变化平缓的区域采用较稀疏的网格从而提高计算效率。
CFD仿真的边界条件主要分为4部分:入口边界条件、出口边界条件、壁面边界条件和对称面边界条件。边界条件的设置如表1所示。

表1 翼型自由流场分析边界条件
1.3 翼型最大相对弯度对翼型气动特性的影响
翼型弯度一般指的是翼型相对弯度。翼型相对弯度为:
(8)
式中:f—翼型中弧线与弦线之间的距离;b—翼型的弦长。
沿着翼型弦线,翼型上的相对弯度是持续变化的,选择翼型的最大相对弯度为研究对象。本研究设计了一个翼型,其基本的参数为:最大厚度为16%,位于30%的翼弦;最大弯度为4%,位于50%的翼弦。仅改变其最大相对弯度分别为4%,8%,12%和16%,弯度不同的4种翼型如图1所示。

图1 弯度不同的4种翼型
本研究对这4个翼型进行CFD分析,研究翼型弯度变化对其气动特性的影响。笔者对图1的4种不同弯度的翼型从攻角0°~25°分别进行CFD分析,得出的负升力-攻角图和升阻比-攻角图分别如图2、图3所示。
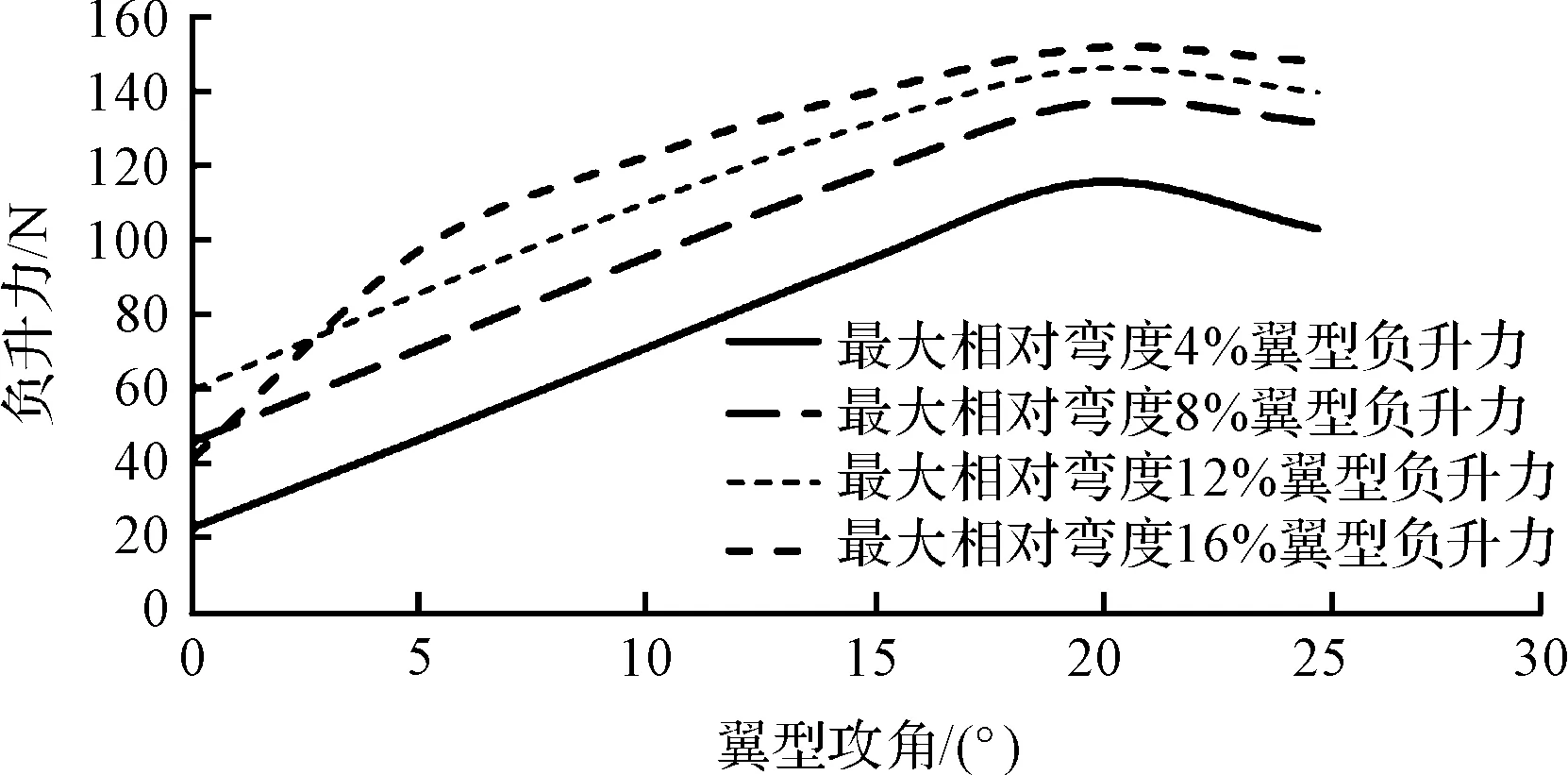
图2 翼型负升力-攻角曲线图

图3 翼型升阻比-攻角曲线图
随着翼型最大相对弯度增大,翼型的最大负升力值也随之增加,改变翼型的最大相对弯度是提高翼型最大负升力最有效的方法之一。当翼型的最大相对弯度为16%时,翼型在小攻角的情况下负升力反而比最大相对弯度为12%的翼型低,这是由于弯度过大的翼型在小攻角的情况下其上表面发生了气流分离。除此区域之外,在任意攻角,最大相对弯度较大的翼型的负升力总是比最大相对弯度较小的翼型大。而它们的失速角并没有明显地改变,保持在20°~22°之间。
升阻比是指翼型负升力与阻力的比值,随着翼型最大相对弯度的增大,其升阻比随之下降,在任意一个攻角,最大相对弯度较大的翼型的升阻比总是比最大相对弯度较小的翼型小。在翼型攻角较小的情况下,最大相对弯度不同的翼型的升阻比值相差较大,但当翼型攻角增大至25°时,最大相对弯度不同的翼型的升阻比都在3.0~3.5左右,相差不大。综合翼型的负升力和升阻比,选择最大相对弯度为12%的翼型为最优翼型。
1.4 翼型最大弯度位置对翼型气动特性的影响
翼型最大弯度的位置一般用百分数表示。改变翼型最大弯度的位置将会改变翼型表面的压力分布,从而在负升力和延缓失速方面进行优化。本研究保持翼型的最大相对弯度为12%,分别改变翼型最大相对弯度位置位于弦线的40%和60%,并对其在攻角0°~25°范围内进行CFD分析,分析翼型最大相对厚度变化对翼型负升力和升阻比的影响。
翼型最大相对弯度分别位于弦线40%、50%和60%的翼型的负升力-攻角图如图4所示。
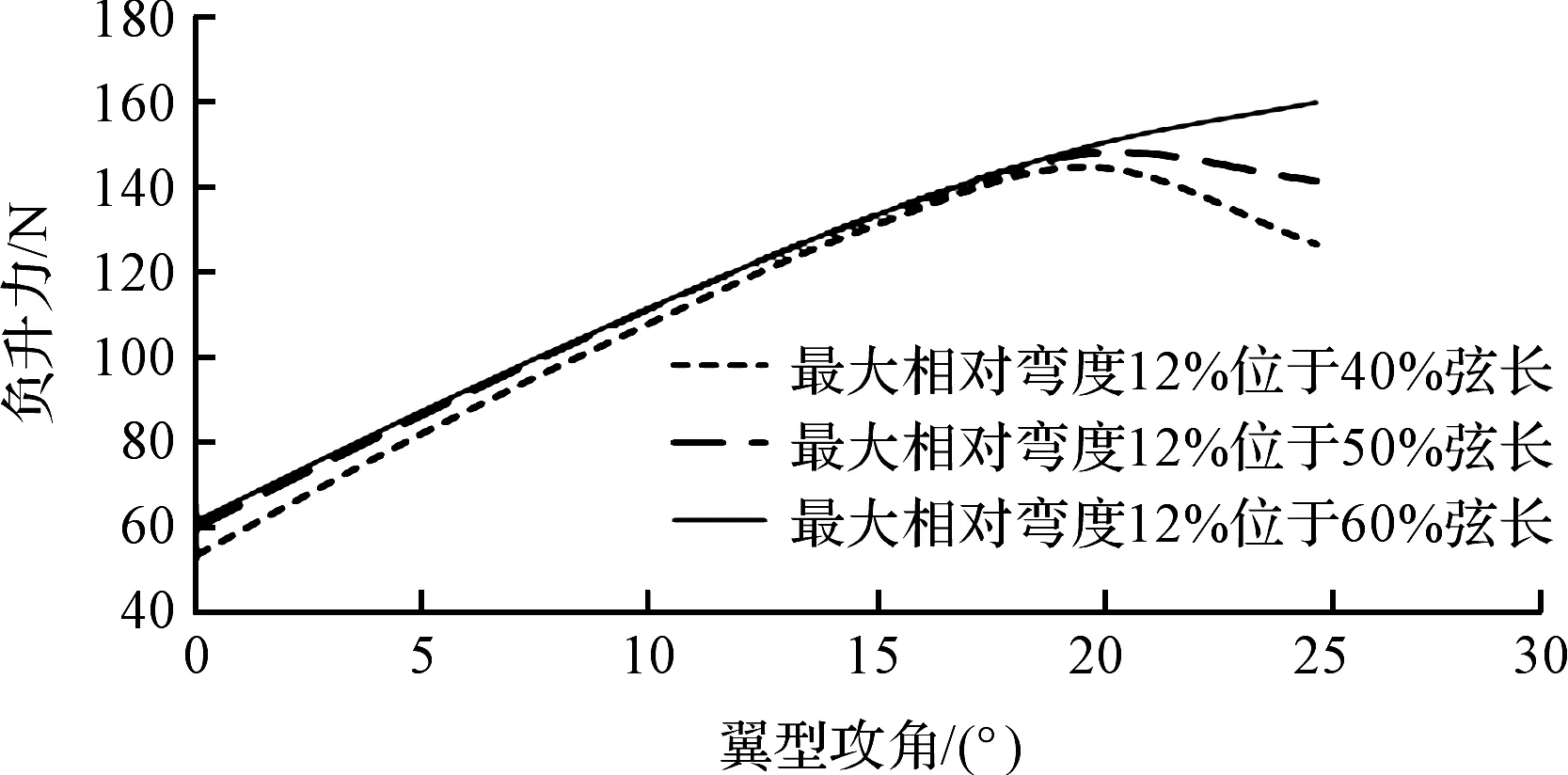
图4 最大相对弯度位置不同的翼型负升力-攻角曲线图
当翼型攻角位于0°~20°之间时,翼型最大弯度位置不同并没有导致其负升力发生明显变化,其负升力-攻角曲线基本保持重合。但当翼型攻角大于20°时,翼型负升力-攻角曲线出现差异,翼型最大弯度位置靠后的翼型能明显延缓翼型出现失速现象,并且其失速曲线也更平缓。
3种最大弯度位置不同的翼型的压力分布和流线云图如图5所示。

图5 翼型压力分布和流线云图
上图可进一步证明,随着翼型最大弯度位置的后移,翼型上开始出现气流分离的分离点也同时后移,同时分离涡出现的区域也进一步缩小。可见,在一定范围内将翼型最大弯度位置后移有助于延缓翼型出现失速现象,增大翼型的失速角。综合翼型的负升力和升阻比等参数,本研究选择最大弯度位于弦线60%的翼型为最优翼型。
2 FSAE赛车尾翼设计和优化
2.1 尾翼翼缝优化
由于单翼片结构在攻角较小的情况下容易发生失速现象,产生的负升力也比较小,FSAE赛车的尾翼一般采用主翼加襟翼的多翼片结构。尾翼的主翼和襟翼翼型通常都是同一个翼型,襟翼的弦长通常为整个尾翼弦长c(主翼的前缘至最后一片襟翼尾缘的距离)的30%~40%[10]。根据《中国大学生方程式汽车大赛规则(2016最终版)》,FSAE赛车的尾翼被限制在长950 mm宽800 mm高1 200 mm的立方体内,因此本研究最终选择主翼弦长为400 mm,襟翼弦长为240 mm。
多翼片尾翼最关键的参数就是它的翼缝,也就是尾翼主翼尾缘与襟翼前缘构成的狭小缝隙。当经过主翼上表面的气流流动至主翼尾缘附近时,狭小的翼缝会使其附近的气流加速通过,而通过翼缝的这部分气流会比流过主翼下表面的气流具有更高的能量。这可以控制翼片的边界层从而延迟气流分离,因而即使襟翼的攻角比较大这部分高能量的气流也能附着在其上。相比单翼片结构,多翼片结构总体的翼片相对弯度更大,大幅提升翼片的失速角,同时产生更多的负升力。本研究取主翼攻角为8°,襟翼攻角为46°。翼缝的大小通常与尾翼的整体弦长c有关,将翼缝的大小分解为襟翼前缘距离主翼尾缘的水平距离和竖直距离,其中水平距离为襟翼前缘超前主翼尾缘的水平距离,垂直距离为襟翼前缘高出主翼尾缘的竖直距离。
笔者研究两翼片结构的翼缝大小,分别取翼缝的水平距离为4%c、5%c和6%c,翼缝的竖直距离取3%c、4%c和5%c(尾翼整体弦长c为590 mm),两翼片结构如图6所示。

图6 两翼片结构
本研究对翼缝的水平距离和竖直距离进行组合,寻求最优的组合结果,以达到最优气动效果。
不同翼缝组合的两翼片结构的阻力、负升力和升阻比值如表2所示。
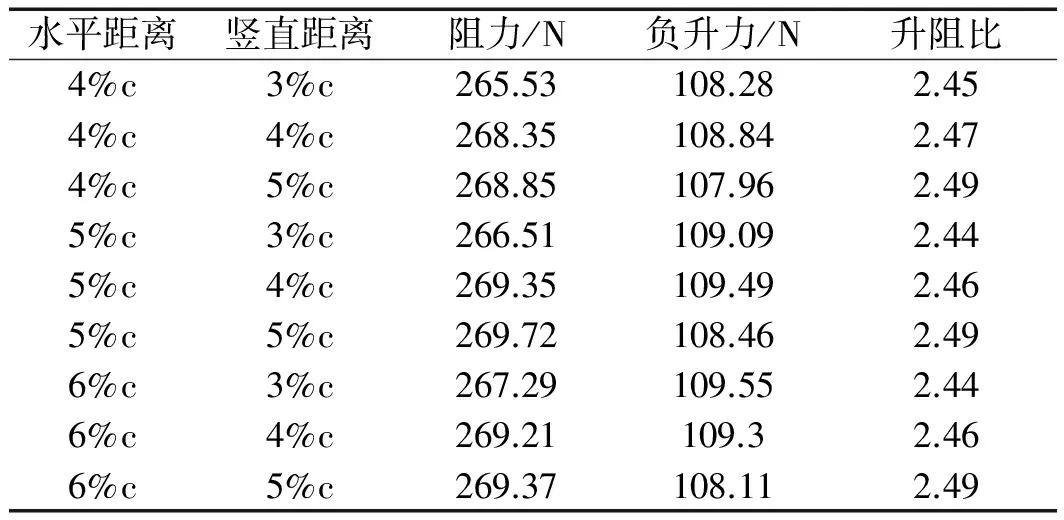
表2 不同翼缝的两翼片结构气动参数
从表2中可以发现,当两翼片结构翼缝的竖直距离为3%c时,随着翼缝的水平距离的增加,两翼片结构的负升力也持续增加。随着翼缝的竖直距离增加,两翼片结构的负升力持续增加,同时其升阻比也保持持续增加,可见,在一定范围内增加翼缝的竖直距离,可以改善两翼片结构的气动特性。翼缝距离分别为水平距离为4%c,竖直距离为3%c和水平距离为5%c,竖直距离为5%c的两种两翼片结构分别对应负升力最小和负升力最大的两翼片结构。结构如图7所示。
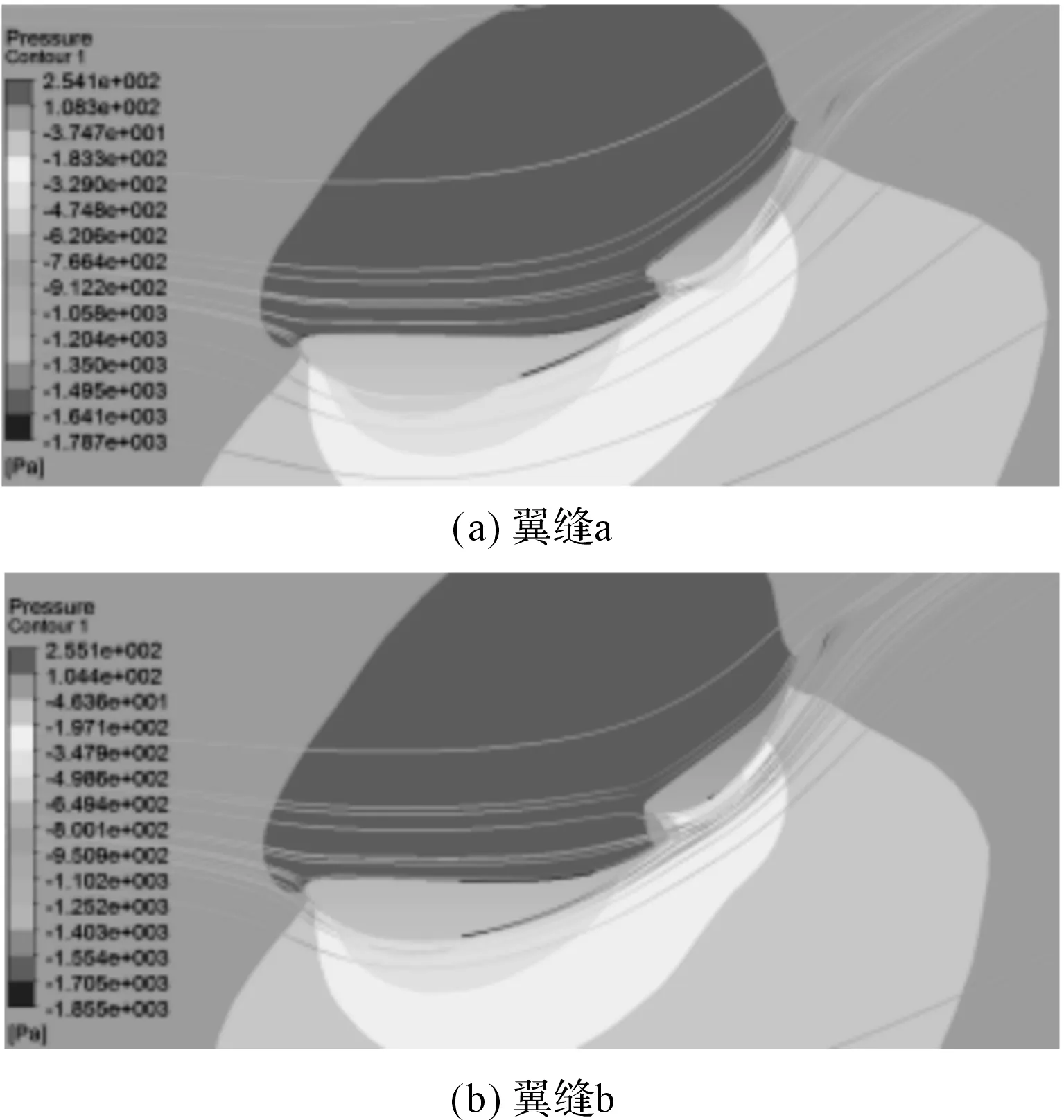
图7 两种不同翼缝的两翼片结构压力云图
从图7中可以发现,适当增加翼缝的距离,能够让更多的气流加速通过翼缝,加速效果也更好,从而延缓气流分离现象的产生。综合两翼片结构的负升力和升阻比等特性,笔者选择翼缝水平距离为5%c,竖直距离为5%c的组合为最优组合。
2.2 尾翼端板优化
当翼片与空气发生相对运动时,会产生诱导阻力,导致尾翼损失一部分的负升力[11]。本研究通常采用添加尾翼端板的方式来抑制诱导阻力的产生[12]。对于FSAE赛车的尾翼,其襟翼的尾缘通常已经比较接近规则所允许的最高高度,因此端板并不能超出襟翼尾缘过多高度,端板只有在翼片下部才具有比较大的设计空间。3种不同端板的尾翼如图8所示,分别对应无端板、较小端板和较大端板3种情况。
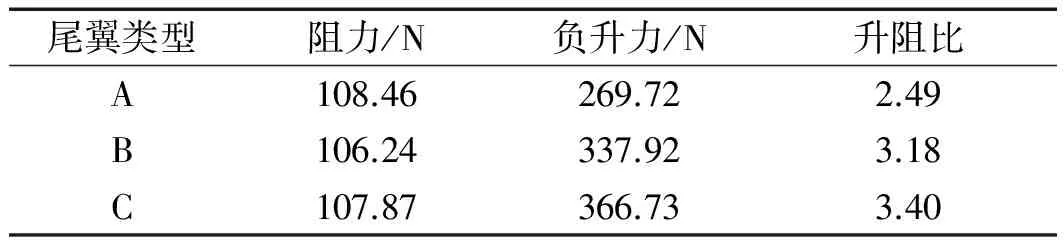
A、B、C3种端板不同的尾翼的阻力、负升力和升阻比值如表3所示。
尾翼类型阻力/N负升力/N升阻比A108.46269.722.49B106.24337.923.18C107.87366.733.40
从表3中可以发现,较小端板的尾翼的负升力相比无端板的尾翼提升了25.3%,较大端板的尾翼的负升力相比无端板的尾翼提升了35.9%。可见,端板可以抑制翼片上表面的高压气流绕流至翼片下表面的低压区,并且,随着端板尺寸的增大,这种抑制现象越明显。尾翼A和尾翼C的流线对比图如图9所示。
图9中无端板的尾翼A在翼片边缘形成了较大的翼尖涡流,导致了翼片上表面高压区压力降低,翼片下表面低压区压力增大。而安装端板的尾翼C则抑制了这个现象,进一步地保护了翼片边缘上下表面的压力差,提高了尾翼的负升力。可见,尾翼C是最优设计。
2.3 多翼片尾翼优化
多翼片尾翼指的是存在两片襟翼或者更多襟翼的尾翼。本研究根据文献[13]设计的一个三翼片的尾翼,如图10所示。
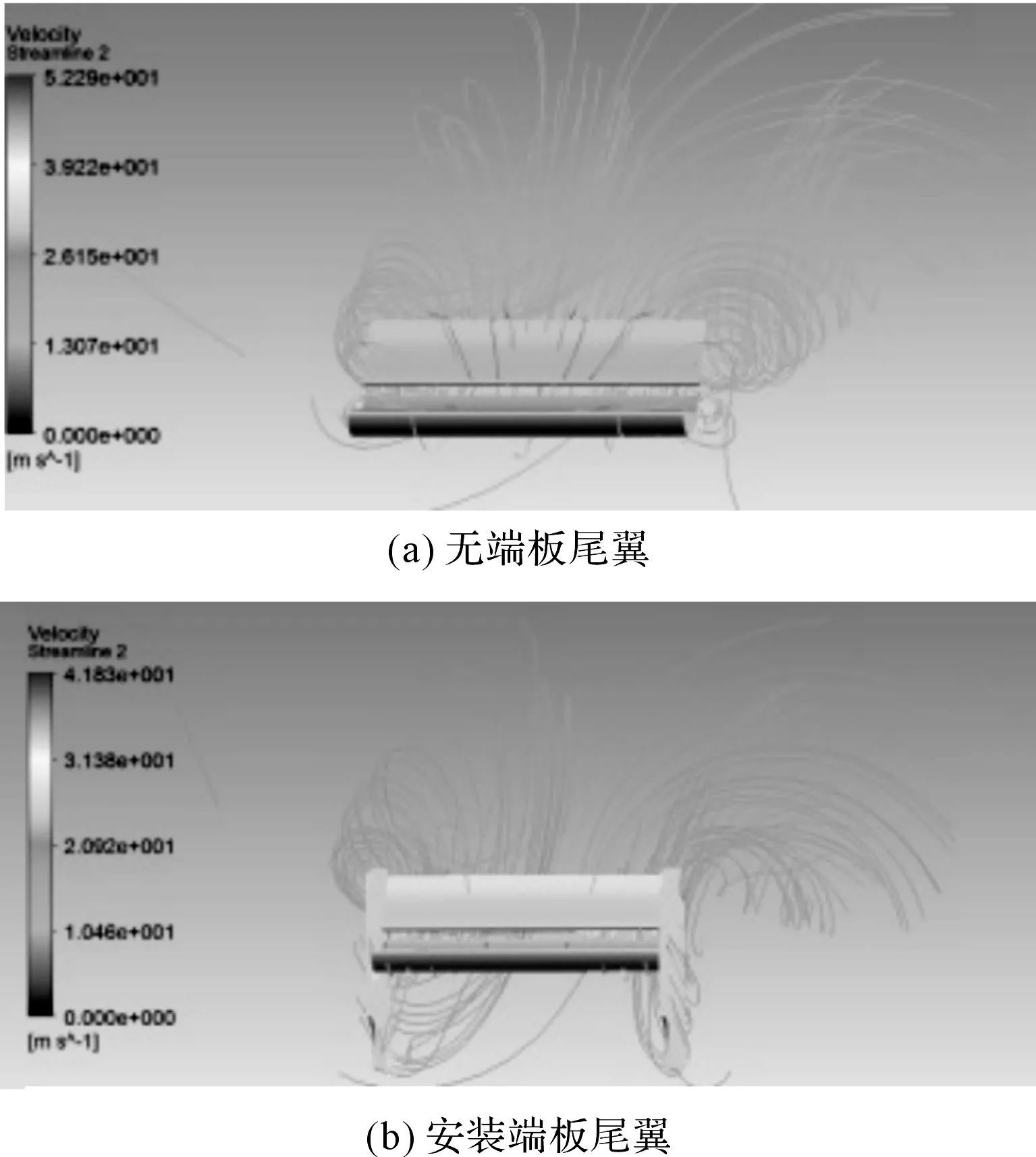
图9 安装端板前后尾翼流线图

图10 三翼片尾翼
其尾翼的总弦长和两翼片尾翼的总弦长保持一致,尾翼总攻角保持为46°,端板保持一致[14-15]。本研究对三翼片尾翼进行CFD分析,并和两翼片尾翼进行对比。两翼片尾翼和三翼片尾翼的气动参数对比表如表4所示。

表4 两翼片尾翼和三翼片尾翼气动参数
从表4中可以发现,在尾翼总弦长和总攻角保持不变的情况下,仅增加尾翼翼片数量,三翼片尾翼的负升力能够比两翼片尾翼增加约7.5%,但三翼片尾翼的阻力也会相应增加约9.7%。需要说明的是,三翼片尾翼的失速角比两翼片尾翼更大,因此三翼片尾翼的总攻角仍有增加的空间,以此来获得更多的负升力。
3 结束语
本研究通过改变翼型的最大弯度以及最大弯度所在位置设计确定符合FSAE赛车的翼型,并对FSAE赛车的尾翼翼缝、端板、多翼片尾翼3个部分通过CFD进行数值分析和对比尾翼的负升力和阻力,从而进行优化。结论如下:
(1)翼型的最大弯度会影响翼型的气动特性,在一定范围内随着翼型的最大弯度增加,翼型的负升力也会随之增加;
(2)翼型最大弯度所在位置也会影响翼型的气动特性,翼型最大弯度所在位置适当后移有利于翼型的气流分离点后移;
(3)翼缝的大小是尾翼设计的关键,当翼缝水平距离为5%c,竖直距离为5%c时,尾翼产生的负升力和升阻比都为最大;
(4)尾翼的端板能够保护翼片边缘部分受到翼尖涡流的影响,从而提升尾翼负升力和升阻比;
(5)三翼片尾翼相比两翼片尾翼能产生更多负升力,但也会产生更多阻力。
[1] 谷正气.汽车空气动力学[M].北京:人民交通出版社,2005.
[2] 马金英,付 强,潘作峰,等.某SUV气动特性仿真分析与试验研究[J].兵工自动化,2015,34(7):33-36.
[3] 余志生.汽车理论[M].5版.北京:机械工业出版社,2009.
[4] KATZ J. Race car aerodynamics: designing for speed[M]. Cambridge: Bentley (Robert) Inc.,1994.
[5] 夏商周.高升力翼型的数值模拟[D].沈阳:沈阳航空工业学院动力系,2006.
[6] 毛 旭,吴宁宁.FSAE赛车新型定风翼型气动性能的提升[J].机械科学与技术,2014,33(9):1397-1402.
[7] YANG Z, GU W, LI Q. Aerodynamic design optimization of race car rear wing[C].2011 IEEE International Conference on Computer Science and Automation Engineering, Shanghai: IEEE,2011.
[8] MCBEATH S. Competition car aerodynamics[M]. London: Motor Books,2006.
[9] WORDLEY S, SAUNDERS J. Aerodynamics for formula SAE: a numerical, wind tunnel and on-track study[R]. New York: SAE Technical Paper,2006.
[10] WORDLEY S, SAUNDERS J. Aerodynamics for formula SAE: initial design and performance prediction[R]. New York: SAE Technical Paper,2006.
[11] REHNBERG S B, RJESSON L, SVENSSON R, et al. Race car aerodynamics-the design process of an aerodynamic package for the 2012 chalmers formula SAE car[R]. New York: SAE Technical Paper,2013.
[12] 马 睿,刘淑莲,郑水英.轴承支座对轴流风机性能试验的影响[J].轻工机械,2016,34(4):83-86.
[13] 柏秋阳,王 辉,李嘉凡,等.FSAE赛车空气动力学套件组合设计分析[J].合肥工业大学学报:自然科学版,2016,39(5):592-597.
[14] 宋世慧,卢洪超,邵万珍,等.车用液力缓速器设计及CFD流体仿真分析[J].液压气动与密封,2016(11):10-13.
[15] 钱 程,谷 波,王 婷,等.电动车前舱冷却模块非均匀风量的数值分析[J].流体机械,2015(12):72-76.

