基于贝叶斯网络的大连市空气质量预测与诊断

化虎蝶，王晨祥

(大连海事大学环境科学与工程学院，辽宁 大连 116026)

近年来，随着我国经济的飞速发展，能源消耗量急剧增加，机动车保有量幅度大增，各种污染物浓度升高，细颗粒物和臭氧的污染加剧，空气污染问题尤为突出。空气污染不仅导致大气能见度降低，空气质量下降，影响人们的正常出行生活，更有研究表明[1]，雾霾中的细颗粒物会增加呼吸系统、心血管系统以及肺癌等疾病的发病风险，威胁人类健康，空气质量问题亟待解决。

解决空气严重污染问题离不开空气质量的有效预测，目前已有多种普遍采用的预测模型，但均存在一些缺陷或不足，如：灰色预测模型仅适用于中长期预测[2]；时间序列预测模型过度突出时间因素在模型中的作用；城市空气污染预报模式系统预报准确率低，仅为68%[3]；人工神经网络模型仅输入输出节点可见，中间节点是隐藏变量，且易发生数据的过拟合，白鹤鸣等基于BP神经网络预测北京市空气污染指数，其预测精度秋季最高，为89%[4-5]。而贝叶斯网络因其具有多源信息综合表达、节点全部可见、双向推理、可处理不完整数据、有效表达变量间的非线性关系等优点，已成为处理不确定性问题的重要工具，广泛应用于智能推理、诊断、决策、预测、风险分析等方面[6]。

大气环境是一个多因素耦合状态下的复杂系统，充满不确定性，将贝叶斯网络引入大气环境质量研究可以有效地处理其不确定性问题。目前国内外关于将贝叶斯网络应用于空气质量预测的研究尚处于探索阶段[7-9]。鉴于此，本文利用大连市2014—2016年空气质量指数(Air Quality Index,AQI)日均值及同期污染物(SO2、NO2、O3、CO、PM10、PM2.5)日均值数据，利用贝叶斯网络技术构建了反映各污染物与空气质量级别之间因果关系及其相互影响的贝叶斯网络模型，对大连市的空气质量进行了预测与评价，以期提供更加准确、客观的空气质量信息，为改善和提高大连市的空气质量提供一定的理论依据。

1 贝叶斯网络简介

贝叶斯网络(Bayesian Networks)最早在1988年由Judea Pearl提出，是一种基于概率论和图论的不确定性推理网络，是复杂联合条件概率分布的图形表达形式[10]。贝叶斯网络是一个二元组S=，由一个有向无环图G以及各节点的条件概率表P组成，有向无环图中变量间因果关系由有向边连接[11]，其中贝叶斯公式是贝叶斯概率计算的基础，即

P(Bi|A)=P(Bi)P(A|Bi)∑ni=1P(Bi)P(A|Bi)

(1)

式中：事件B1，B2，…，Bn均为样本空间Ω的划分，两两互斥，且P(Bi)>0；P(Bi)为事件Bi发生的概率；P(A|Bi)为在已知事件Bi发生时，事件A发生的概率。

贝叶斯网络的组成和构建分为三个步骤：①确定变量节点和变量域；②贝叶斯网络学习，包括结构学习和参数学习，确定网络拓扑图和条件概率表；③贝叶斯网络推理[12-13]。

2 贝叶斯网络预测模型的构建

2. 1 预测因子选取

我国目前采用空气质量指数(AQI)来表征空气质量状况，对空气污染的程度进行分级，提示对人体健康的影响，参评的污染物包括6种：二氧化硫(SO2)、二氧化氮(NO2)、臭氧(O3)、一氧化碳(CO)、可吸入颗粒物(PM10)、细颗粒物(PM2.5)，根据6种参评污染物浓度计算得出空气质量分指数(Individual Air Quality Index,IAQI)，从中选取最大值为空气质量指数AQI，取值的范围为0～500。由于6种污染物来源广泛、成分复杂[14]，使空气质量的预测充满不确定性。

污染物是导致空气质量下降的最直接原因，也是确定大气环境质量等级的依据，因此本文选取6种污染物为空气质量预测模型的预测因子与AQI共7个随机变量,并利用公式(2)计算各预测因子与AQI的互信息值(Mutual Information,MI)(见表1)，度量预测因子与AQI间的依赖程度，互信息阈值设为0.01Bits[15-16]。互信息计算公式为

MI(X,Y)=∑rii∑rjjp(xi,yj)logp(xi,yj)p(xi)p(yj)〗

(2)

式中：X、Y为随机变量；ri、rj分别表示随机变量X、Y的取值个数；xi、yj分别表示随机变量X、Y取第i、j个的属性值；p(xi、yj)为X、Y状态分别为xi、yj时的概率；p(xi)、p(yj)分别表示X、Y状态分别为xi、yj时的概率。

表1 预测因子与AQI间的互信息值

由表1可见，各变量的互信息值均大于0.01Bits，表明选取的各变量作为大连市空气质量主要预测因子是恰当、合理的。

2. 2 数据离散化

贝叶斯网络方法与其他许多机器学习算法、分类算法一样需要处理样本数据的离散属性，故需要对样本数据进行离散化处理，本文对样本数据的离散化处理主要依据《环境空气质量标准》(GB 3095—2012标准)、专家知识等，各变量离散化后的标准属性值见表2。

表2 空气质量预测因子离散化后的标准属性值

将各变量划分为4个等级，分别为1级、2级、3级、4级，其中AQI对应的4个等级分别表示空气质量清洁、优良、污染和重污染。

本文以收集到的大连市2014—2016年的空气质量相关数据为样本数据，本着若观测数据中一个值缺失，则取前后两个数据的平均值，连续三个数据缺失，则将其剔除的原则，对数据进行清洗后，得到可用数据为1 096组。总数据包括训练数据和验证数据两部分，其中训练数据用于构造贝叶斯网络模型，验证数据用于模型验证，同时对2017年5月1日至15日大连市的空气质量进行了预测与分析。

2. 3 贝叶斯网络结构学习

将贝叶斯网络工具箱(Bayes Net Toolbox,BNT)[17]导入MATLAB软件进行贝叶斯网络模型的构建和推理，确定变量节点与变量域后，选择1992年Cooper等提出的基于贝叶斯评分与爬山搜索的K2算法[18]学习网络结构，这是一个结构优化的过程，即利用评分函数找到与已有数据匹配程度最高的结构。该算法要求给定节点顺序，利用贝叶斯评分评价模型与数据的匹配度，进而通过爬山搜索找到最佳网络结构，节点顺序由前文计算的互信息值确定。然而完全依赖数据构建网络结构不是很可靠[19]，故还需要结合专家知识对网络结构进行调整。

由于搜索评分算法本身的弱点，使用K2算法从数据中学习网络结构后，变量节点间可能存在多边、少边、或者弧方向的错误[20]，故结合专家知识并查阅相关研究后，对仿真出的网络结构进行了适当调整。鉴于BNT可视化能力的限制，本文在MATLAB软件中仿真出网络结构后，结合微软贝叶斯网络工具箱绘出网络结构并进行推理，得到贝叶斯网络结构，见图1。

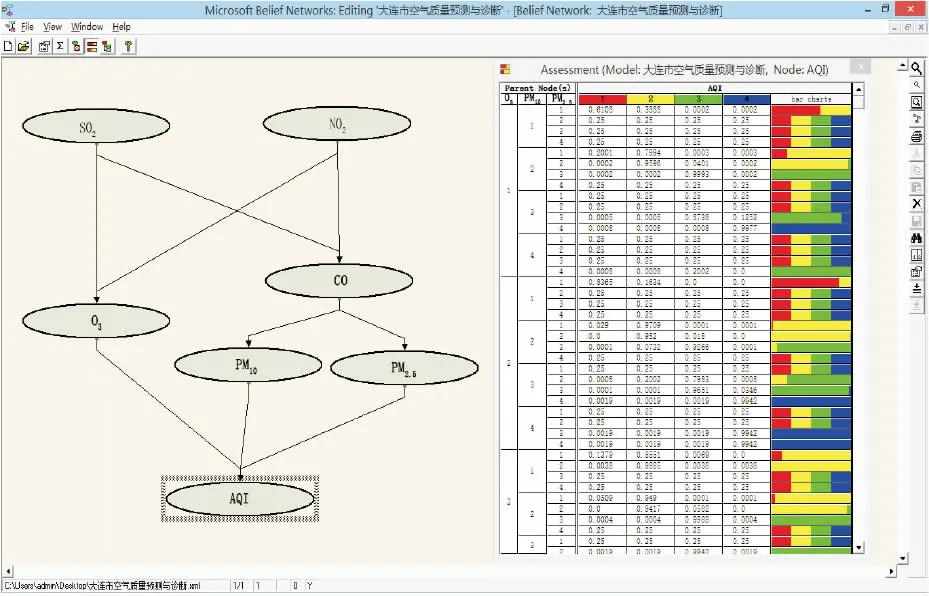
图1 贝叶斯网络结构Fig.1 Bayesian Network structure

由图1网络结构中有向边的指向关系可知，预测因子间存在着直接或间接的因果影响关系， 例如对于预测因子中的O3，SO2和NO2对其均有直接影响，而其又直接影响AQI；对于网络结构中目标节点AQI,直接对其产生因果影响的预测因子为O3、PM10、PM2.5,而SO2等其他3个预测因子与AQI间存在间接的因果关系。

2. 4 贝叶斯网络参数学习及推理

贝叶斯网络结构构建完成后，需要选择合适的参数学习算法从数据中挖掘每个变量的条件概率分布。由于网络结构中所有变量均可以观察且数据完整，故选用最大后验算法(Maximum A Posteriori，MAP)计算变量的先验概率及条件概率[21]。本文充分利用贝叶斯网络的双向推理能力，选择联合树推理算法[22-23]进行推理，一方面用因果推理验证模型的有效性和预测准确性，另一方面用诊断推理分析预测因子在不同的空气质量级别下发生的概率，并分析大连市空气污染的主要贡献者。

首先从总体样本中随机选取986组数据，运用MAP法对大连市空气质量进行贝叶斯网络参数学习，完成贝叶斯网络预测模型的构建，并用未参与训练的110组数据验证模型的有效性；同时，由于大连市AQI以及6种污染物具有显著的四季变化特征，故对春(3～5月)、夏(6～8月)、秋(9～11月)、冬(12～次年2月)四季分别建立了贝叶斯网络预测模型，为了使预测模型具有良好的合理性和代表性，训练数据采用从各季节的数据集中随机选取的方法，春、夏、秋、冬四季分别选取248组、248组、246组、244组训练数据，28组、28组、27组、27组测试数据；最后运用贝叶斯网络的诊断推理功能，分析在不同的空气质量级别下6种污染物发生的概率，从概率的角度解释污染物在不同的空气质量级别下发生的概率，并确定大连市空气污染的主要贡献者。

3 预测结果与分析

3. 1 贝叶斯网络模型的验证

根据建立的贝叶斯网络预测模型，利用未参与训练的测试数据进行验证，若验证值与监测值处于同一等级，则认为模型具有有效性。利用建立的贝叶斯网络模型对大连市全年和春、夏、秋、冬四季的空气质量进行了验证，其验证结果见图2和图3。

由图2可见，大连市全年验证组数据85%以上的验证值与监测值处于同一等级，即验证准确；统计失真的12组数据发现，验证值与监测值差值均为1级，说明得出的验证值较监测值偏差不大。

图2 利用贝叶斯网络模型对大连市全年的空气质量验证结果Fig.2 Validation results of Bayesian Network model for the annual air quality of Dalian City

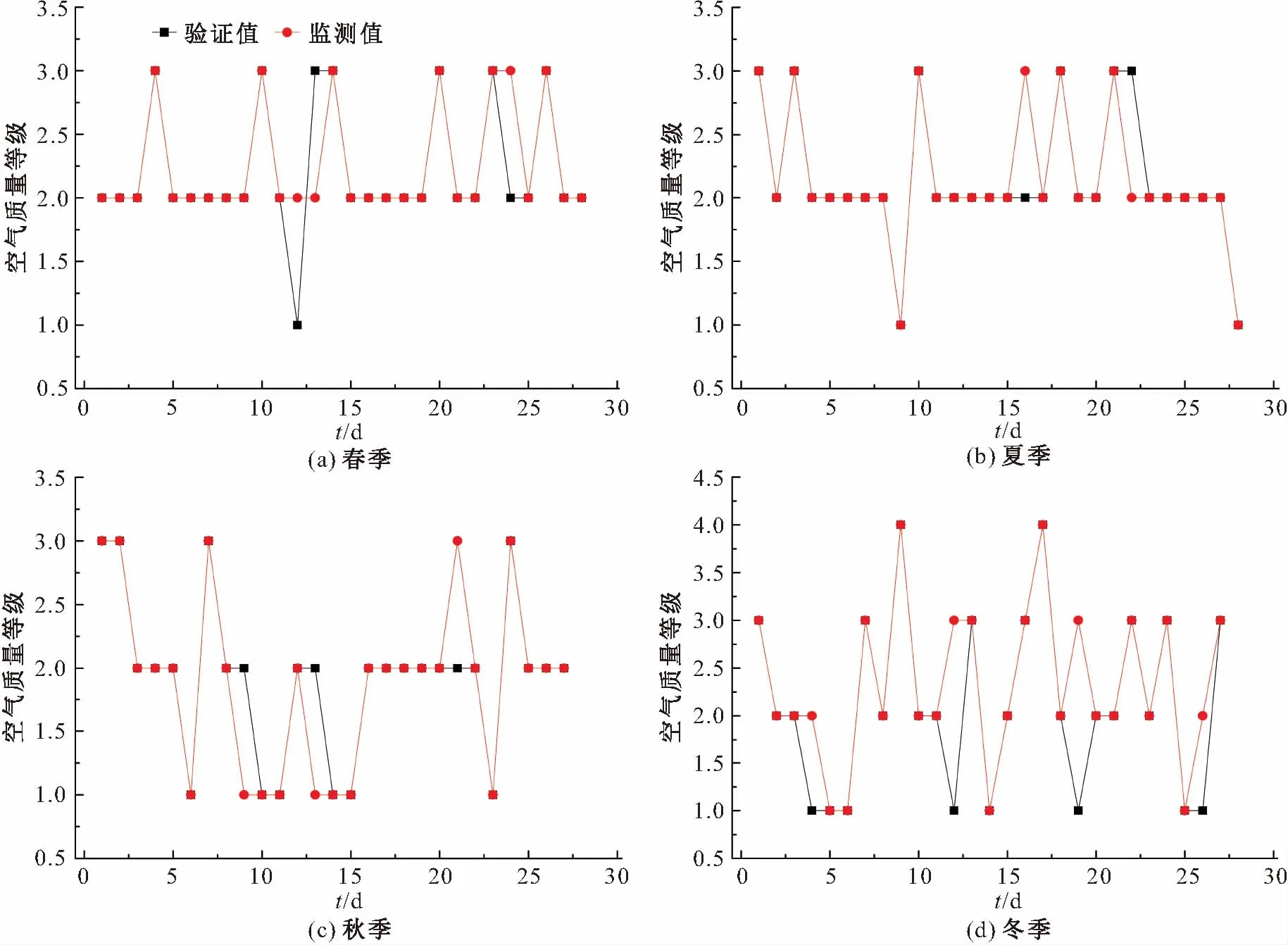
图3 利用贝叶斯网络模型对大连市四季的空气质量验证结果Fig.3 Validation results of Bayesian Network model for seasonal air quality of Dalian City

由图3可见，整体上大连市春、夏、秋、冬四季验证组数据85%以上的验证值与监测值处于同一等级，即验证准确；统计失真组数据发现，春、夏、秋季验证值与监测值的差值均为1级，冬季最大差值出现2级，说明冬季模型的预测精度较低。

本文将贝叶斯网络模型对大连市春、夏、秋、冬四季和全年空气质量的预测结果与模糊综合评价法的预测结果进行了对比，并分析了两种方法的预测精度，详见表3。

表3 两种方法预测精度对比(%)

由表3可见，贝叶斯网络模型对大连市春、夏、秋、冬四季和全年空气质量的预测精度分别为89.29%、92.86%、88.89%、85.19%、89.09%，均高于模糊综合评价法；冬季的预测精度为85.19%，低于全年的预测精度89.09%。分析影响贝叶斯网络模型预测精度的因素主要有离散区间划分、训练数据量的限制等。此外，大连市秋冬季节燃煤供暖，造成空气污染严重，空气质量级别变化大，也是冬季贝叶斯网络模型的预测精度在四季中最低的原因；同时由于大连市的降水60%～70%均发生在夏季，故夏季构建的贝叶斯网络最具有代表性，其模型预测精度在四季中也最高。

3. 2 贝叶斯网络模型的预测

本文利用构建的贝叶斯网络模型对大连市2017年5月1日至15日的空气质量进行了预测，即通过输入数据，更新条件概率，得出AQI的后验概率，并按照概率取最大值的原则将概率值转换为对应的空气污染级别，从而得到了预测结果。本文将贝叶斯网络模型的预测结果与模糊综合评价法的评价结果和官方的监测值进行了对比，详见表4。

表4 贝叶斯网络模型与模糊综合评价法预测结果的比较

由表4可见，贝叶斯网络模型的预测结果优于模糊综合评价法，两者预测精度分别为86.67%、66.67%；贝叶斯网络模型预测失真组的预测值与监测值的差值均为1级，而模糊综合评价法预测失真组的预测值与监测值的差值差别较大，且基本发生于极端天气，而贝叶斯网络模型基本不受极端天气的影响。整体上表明贝叶斯网络模型对大连市空气质量的预测具有良好的泛化能力和预测精度。

3. 3 贝叶斯网络模型的诊断

本文在建好的贝叶斯网络模型中，通过贝叶斯网络的诊断推理功能分析了大连市空气质量处于不同级别时各污染物发生的概率，其结果见图4。

图4 大连市各污染物发生的概率与空气质量级别的 因果关系图Fig.4 Probability chart of the pollutants with different air quality levels in Dalian City

由图4可见，当空气质量为污染等级时，处于前三位的概率为0.732 9>0.683 3>0.656 5，对应的污染物分别为O3、PM2.5、PM10,即空气处于污染等级时，三者中O3发生的概率最大，PM2.5次之，PM10发生的概率最小；当大连市空气质量为重污染等级时，处于前三位的概率为0.748 2>0.728 7>0.724 9，对应的污染物分别为PM2.5、O3、PM10，即空气处于重污染等级时，三者中PM2.5发生的概率最大，O3次之，PM10发生的概率最小。由此说明PM2.5和O3是大连市空气污染的主要贡献者。

4 结论与建议

(1) 本文针对大连市空气质量建立了四季和全年的贝叶斯网络预测模型，并利用贝叶斯网络的因果推理功能对建立的贝叶斯网络模型进行了验证，结果表明：贝叶斯网络模型对大连市四季和全年空气质量的预测精度均高于85%，说明该模型能从概率的角度较好地描述空气质量与各污染物间的非线性关系，故将贝叶斯网络应用于空气质量预测是可行的。

(2) 本文利用建立的贝叶斯网络模型预测了大连市2017年5月1日至15日的空气质量，并与模糊综合评价法的预测结果进行了对比，结果表明：贝叶斯网络模型的预测精度更高，且模型预测失真组的误差较小，模型的预测结果基本不受极端天气的影响。

(3) 本文利用贝叶斯网络的诊断推理功能分析了造成大连市空气质量下降的主要污染物，从概率的角度得出PM2.5和O3是大连市空气污染的主要贡献者。而燃煤、汽车尾气以及工业排放等是大连市大气污染物的主要排放源，污染源排放出颗粒物等一次污染物的同时还会生成一些细颗粒物、臭氧等二次污染物。故建议大连市应加强空气质量的监测，建立更全面的空气污染预警预报机制，同时准确查明主要污染物来源，强化污染物排放管控，以提高空气质量。

(4) 本文将贝叶斯网络引入到城市空气质量预测研究中，利用数据样本构建网络结构，使推理结果更加准确，目前还未见有相关文献，故本文尚属于探索性研究。但由于受数据样本的限制等，本文只选取了6种污染物作为预测因子，在今后的研究中还需要进一步考虑气象因子、区域环境因子等对城市空气质量的影响。另外，本文利用贝叶斯网络模型只是对空气质量等级做出预测，并未预测出空气质量指数，从而影响了模型的预测精度，且导致模型应用存在一定的局限性，这将是今后需要进一步研究的方向。

[1] 阚海东.雾霾天气下的细颗粒物污染和居民健康[J].中华预防医学杂志,2013,47(6):491-493.

[2] 陶兴焕,陈志德.灰色理论模型在环境空气质量预测中的应用[J].环境,2013(S1)：45,51.

[3] 朱玉强.几种空气质量预报方法的预报效果对比分析[J].气象,2004,30(10):30-33.

[4] 白鹤鸣,沈润平,师华定,等.基于BP神经网络的空气污染指数预测模型研究[J].环境科学与技术,2013(3):186-189.

[5] 张茹,张学杨,陆洪光,等.基于层次分析和主成分分析的城市空气质量评价——以徐州市为例[J].安全与环境工程,2017,24(3):103-107.

[6] Jensen F V.IntroductiontoBayesianNetworks[M].Berlin:Springer,1996.

[7] 王勤耕,夏思佳,万祎雪,等.当前城市空气污染预报方法存在的问题及新思路[J].环境科学与技术,2009,32(3):189-192.

[8] 刘志龙,诸雪征,梁婷,等.基于贝叶斯网络的大气环境质量评价模型研究[C]//全国风与大气环境学术会议论文集.北京：中国气象学会，2008:486-491.

[9] 夏思佳.中小城市空气质量概率预报方法研究[D].南京：南京大学，2010.

[10]张连文,郭海鹏.贝叶斯网引论[M].北京：科学出版社,2006:31-44.

[11]Marchette D J.Bayesian networks and decision graphs[J].Technometrics,2003,45(2):178-179.

[12]易玉枚,廖可兵,易灿南.基于BN的模糊系统事故风险管理辅助分析[J].安全与环境工程,2015,22(3):105-110.

[13]Darwiche A.Bayesian networks[J].CommunicationsoftheACM,2010,53(12):80-90.

[14]郝津川,李伟.大气PM2.5的污染特征及防控治理[C]//2014中国环境科学学会学术年会.成都：中国环境科学学会，2014:1-5.

[15]Viola P A,Wells Iii W M.Alignment by maximization of mutual information[J].InternationalJournalofComputerVision,1997，24(2):137-154.

[16]金焱,胡云安,张瑾,等.互信息与爬山法相结合的贝叶斯网络结构学习[J].计算机应用与软件,2012,29(9):122-125.

[17]Murphy K P.The Bayes Net Toolbox for Matlab[J].ComputingScience&Statistics,2001,33:2-8.

[18]Cooper G F,Herskovits E.A Bayesian method for the induction of probabilistic networks from data[J].MachineLearning,1992,9(4):309-347.

[19]黄影平.贝叶斯网络发展及其应用综述[J].北京理工大学学报,2013,33(12):1211-1219.

[20]Heckerman D,Dan G,Chickering D M.Learning Bayesian networks:the combination of knowledge and statistical data[J].MachineLearning,1995,20(3):197-243.

[21]Sun X,Druzdzel M J,Yuan C.Dynamic weighting A* search-based MAP algorithm for Bayesian networks[C]//Proceedingsofthe20thInternationalJointConferenceonArtificialIntelligence.San Francisco,CA,USA:Morgan Kaufmann Publishers Inc.,2007:2385-2390.

[22]Pearl J.Non-bayesian Formalisms for Managing Uncertainty—Probabilistic Reasoning in Intelligent Systems[M]//Pearl J.ProbabilisticReasoninginIntelligentSystems:NetworksofPlausibleInference.San Francisco,CA,USA:Morgan Kaufmann Publishers Inc.,1988:415-466.

[23]Kahle D,Savitsky T,Schnelle S.Junction tree algorithm[EB/OL].(2008-09-09)[2017-07-17].https://www.cs.helsinki.fi/u/bmmalone/probabilistic-models-spring-2014/JunctionTreeKahle.pdf.