重视“手脑操作”，促进思维发展

顾云燕

【摘 要】积累数学基本活动经验是义务教育阶段数学课程的重要目标之一，教师只有在数学教育教学中重视数学活动，才能够帮助学生在数学活动中逐步积累基本活动经验。教师可以从“动手操作，积淀数学基本活动经验；脑力操作，内化数学基本活动经验；回顾反思，提升数学基本活动经验；联想激活，运用数学基本活动经验”等方面加以重视，以期有效积累学生数学基本活动经验。

【关键词】小学数学；操作；活动经验

《义务教育数学课程标准（2011年版）》提出了在数学教学中使学生逐步积累“数学基本活动经验”，把“积累数学基本活动经验”作为义务教育阶段数学课程的一个重要目标，明确了教师在数学教育教学中要高度重视数学活动，使学生在数学活动中积累基本活动经验。那么如何实现学生数学基本活动经验的有效积累呢？这当然离不开学生的手和脑。

一、動手操作，积累数学基本活动经验

“儿童的智慧在指尖上。”动手操作能让学生在体验的同时获得直接经验，促进思维的发展。数学活动经验，是学生不断经历、体验各种数学活动过程的结晶，只有在不断的“做”和“思考”的过程中才能积累起来。

【教学片段1】长方体的认识

师：同学们，如果让你们搭一个长方体框架，你认为需要几根小棒？为什么？任意长度可以吗？

生：需要12根，因为长方体有12条棱。

生：任意长度肯定是不可以的，棱的长短也有关系的。

师：我们用12根小棒代表长方体的12条棱，现在有4组小棒可以选，你打算选哪一组，为什么？

学生冷静观察、思考，然后各组长选择小棒，并开始操作活动。

师：你们搭出了怎样的长方体框架？

生：我们选的是第一组小棒，搭出了一个长9cm、宽7cm、高4cm的长方体。

师：在搭的过程中你们需要几种长度的小棒，每种需要几根？请同学上来数一数。

生：我们选的是第三组小棒，也搭成功了，但搭出的长方体和第一组小棒搭出的长方体框架不一样，它有8条棱长度是相等的，4个面的大小一样。

师：有搭了不成功的吗？（有几个小组举手了）

师：同样是12根小棒，为什么你们小组搭不成长方体框架呢？

生：我们选择的是第四组小棒，有1根小棒太短了。

生：我们选择的是第二组小棒，有1根太长。

师：请不成功的小组来老师这里换一根你需要的小棒，完成长方体框架的搭建。想一想，怎么换？（换后快速完成搭建）

师：我还为大家准备了一些长方形和正方形纸片，如果把你们的长方体框架贴上纸片，你需要几张？

生：6张，因为有6个面？

师：你需要怎样的6张纸片？

生：长方体相对的两个面完全相同，所以只要3种纸片，每种2张。

生：我们只要2种纸片，因为这个长方体框架有2个面是正方形，其他4个面是完全相同的长方形。

师：你们思考得很细致，那怎么选纸片的大小呢？

生：根据棱的长度来确定。

师：下面就请同学们从老师提供的多种纸片中选取合适的纸片。

学生开始分组选纸片贴面。

在操作前选小棒，引导学生不要盲目动手，要学会冷静思考后再动手。手脑合用，既是对长方体“棱”认识的知识经验的积累，又是智慧操作的经验积累。在搭建完长方体框架后，学生选择合适的“面”，使长方体面面俱到。

数学教学内容是抽象的，对于具体形象思维占优势的小学生来说，动手操作是他们学习数学的重要方式之一。在具体的教学过程中，教师要根据学习内容及学生特点，合理选择、组织操作活动，扎实推进操作活动的开展，让学生在亲历中体验“做数学”，在体验中实现数学的“再创造”，积累扎实的数学基本活动经验。

二、脑力操作，内化数学基本活动经验

有了思维的碰撞、心灵的感悟，数学活动经验才能真正得到内化。数学课堂应是开放的灵动的，是充满情感、富于思考的经历体验和探索活动。我们设计的数学活动如果让学生的思维仅停留于感性经验的层面上，就不能在感性认识中揭示、获取理性的经验。因此教学中不仅要让学生充分参与探究活动，更要适时地引导学生观察、思考、发现、比较，让他们用心去体验数学、感悟数学，内化为数学活动经验 。

【教学片段2】烙饼问题

师：通过刚才的活动我们知道了烙三个饼，有花12 分钟的，也有省时花9分钟的。

下面我们再来回顾刚才的两种烙法，看看时间是怎样省出来的？（课件展示两种烙法的过程）

师：比较一下，第二种方法它能省出3分钟，这是为什么？请你想一想。（学生轻声交流）

生：因为用时12分钟的那种，第三次烙时，锅里能放两个，但它只放了一个，所以多花了时间。

师追问：那第二种烙法为什么能省时呢？

生：第二种烙法，因为每次都把锅里都装满了，没空出位置来。

师追问：那么再想一想，第二种烙法是怎样做到不让它空出来，不浪费的？

生：第一种烙法中，第3个饼的正反两面是不能同时烙，第二种烙法为了不使锅空出位置在第二个3分钟的时候把第3个饼和第2个饼烙的顺序交换了一下，这样就能使锅里每次都有两个饼。

师：说得非常好，交换一下两个饼烙的顺序，就使锅不空出位置，节省了时间。

师：通过刚才的学习活动，你有什么收获吗？

生：要节省烙饼的时间，锅里不能空出位置来，最好锅里一直都有两个饼。

……

如果说数学知识可以通过传授获得，那么数学活动经验的积累、数学思想方法的获得，更多的是要靠学生自身的体验与感悟。在前期的活动中得出了烙三个饼最少花9分钟这一结论后，教师并不止步于此，还引导学生通过对12分钟与9分钟的烙法的比较，有意识地引导学生思考 “时间是怎样省出来的，怎么办到的？”让学生去思考、交流，让思维在交流中碰撞，智慧在交流中生成，使学生对统筹优化思想有更深的体验和感悟。

只有在思维充分碰撞、方法不断交流感悟中，数学活动经验才能真正内化。教学中设计的数学活动必须有思考价值，能有效地调动和活跃学生的思维，才能促进学生深刻理解、建构知识，达成数学活动经验的内化。

三、回顾反思，提升数学基本活动经验

荷兰著名教育家弗赖登塔尔说过：“反思是数学的重要活动，是数学活动的核心与动力。如果说数学是思维的体操，那么反思则是思维体操中的高级动作。”学生经历了数学活动，获得了一些数学活动经验，但往往是零散的、模糊的、粗浅的、浮于表面的，这就需要教师引导学生进行回顾反思，以促进活动经验的内化。

【教学片段3】圆柱与圆锥练习课

出示习题：求右图中梯形绕轴旋转后形成的图形的体积。

学生独立解答。

师：谁来说说你是怎样列式的？

生： 3.14×6×6×8+3.14×6×6×（12-8）×[1/3]。

師：同意吗？

许多学生表示同意，只有个别学生表示反对。

师：我们先不讨论，请你们试着做一做下面的这道题。求右图中梯形绕轴旋转后形成的图形的体积。

有的学生一脸茫然，嘴里嘀咕说：“不是一样的吗？”而有的学生思考后豁然开朗，忙于改正第一题。

师出示下面三个问题：

（1）两道题目有什么不同？

（2）想象一下，它们旋转后各自形成了怎样的图形？

（3）3.14×6×6×8+3.14×6×6×（12-8）×[1/3]它究竟是哪一题的正确列式呢？为什么？

组织学生思考讨论。

师：来说说你的想法？

生：这两道题是不一样的，虽然是同一个梯形，但绕的轴不一样，得到的立体图形是不同的。

生：第一幅图旋转后得到图形是一个底面半径为6cm、高为12cm的圆柱挖去了一个底面半径6cm、高4cm的圆锥。

生：第二幅图旋转后得到的图形是一个底面半径为6cm、高为8cm的圆柱加上一个底面半径6cm、高4cm的圆锥。

生：3.14×6×6×8+3.14×6×6×（12-8）×[1/3]应该是第二题的正确列式，第一题应该是3.14×6×6×12-3.14×6×6×（12-8）×[1/3]。

师：看来这两题并不难，同学们已经理解了。可是刚才一开始为什么你会犯这样的错误呢？你觉得解答这类题目要注意些什么？

生：一开始我没有认真观察图形，以为图形旋转后得到的都是下面是一个圆柱形，上面是一个圆锥形。

生：我没有仔细看题目，看到这题就以为和原来做过的题目类似，想当然就做了。

生：以后碰到问题时，要静下心来，仔细观察，认真审题，然后再选择合适的方法进行计算，避免犯类似的错误。

生：千万不能想当然，一定要认真审题。

当学生认识了自己的错误解法，学生就多了一种对错误的“免疫力”。而当学生分辨出对错后，教师没有“见好就收”，而是“乘胜追击”。引导学生反思为何会犯错，思考经历了这次犯错纠错活动以后要注意些什么？学生学会将活动所得经验不断内化和概括，最终迁移运用到其他活动和学习中去。

活动后引导回顾反思，培养反思意识应成为学生积累活动经验过程中的常态。因为它对于学生学习能力的发展具有重要的价值，能有效提升基本活动经验，给予学生学习生长的力量，让学生终身受益。

四、联想激活，运用数学基本活动经验

学生数学活动经验的积累，最终目的是解决问题，为学生的可持续发展提供服务。但是，学生的数学活动经验往往是“内隐”的，处于”蛰伏”状态，因此，往往需要教师采取有效手段去唤醒、去激活，让学生的数学活动经验发挥作用，为他们的数学学习服务。

【教学片段4】平面图形的面积练习课

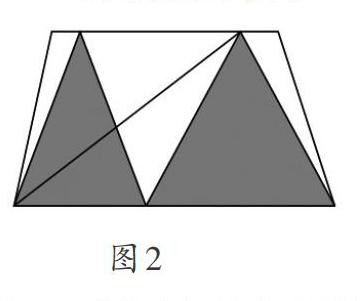
出示习题：求下面阴影部分的面积（见图1）。

师：请同学们仔细观察图形，求出阴影部分的面积。

由于没有告诉这两个三角形的底分别是多少？许多学生一时没有找到解决的办法。

师提示：同学们还记得我们是怎样推导出平行四边形、三角形、梯形的面积计算公式的吗？

生：我们是用转化的方法推导出平行四边形、三角形、梯形的面积计算公式的。

师：我们想一想是否也可以用转化的方法来解决这个问题呢？

学生思考、解答并交流。

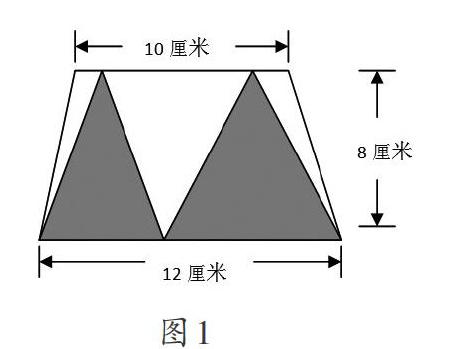
生：我是把左边的三角形转化成与它同底等高的三角形（见图2），这两个三角形的面积相等，而新转化成的三角形又与原右边三角形拼成了一个底是12厘米、高是8厘米的三角形，所以阴影部分的面积就是12×8÷2=48（平方厘米）。

生：我是像图3一样添上几条辅助线，把梯形变成一个长12厘米、宽8厘米的长方形，而图中的阴影部分正好与图中的空白部分相等，所阴影部分的面积就12×8÷2=48（平方厘米）。

生：我是假设左边三角形的底是a，右边三角形的底是b，那么阴影部分的面积就是a×8÷2+b×8÷2，我们知道可以利用乘法分配律a×8÷2+b×8÷2=（a+b）×8÷2，而a+b=12，所以三角形的面积是12×8÷2=48（平方厘米）。

数学学习过程是个体的数学认知结构进行组织再组织的过程。教师提出的“同学们还记得我们是怎样推导出平行四边形、三角形、梯形的面积计算公式的吗？”这一问题， 好似“一语惊醒梦中人”，学生头脑中化未知为已知的转化活动经验被唤醒、激活，想到可以运用等积变形、倍积变形的方法来解决该问题。我们可以看到在运用数学活动经验解决问题的过程中，学生的思维从混沌到清晰、从碰撞到融合，真正成为一个探索者、发现者。

当学生面对问题束手无策时，教师要采取有效的方式，激活学生已有的数学活动经验，使学生的学习基于经验而又超越经验，完善数学活动经验。

积累数学基本活动经验是一个长期的过程，需要我们在平时的教学中不断为学生提供活动的机会，精心设计组织好每一个数学活动，使数学学习成为一个生动活泼、富有创造意义的过程，促进学生思维的发展。

（浙江省桐乡市茅盾实验小学 314500）