时序分析在制导炸弹测试数据判读中的应用

张瑞 刘怀勋 魏志刚

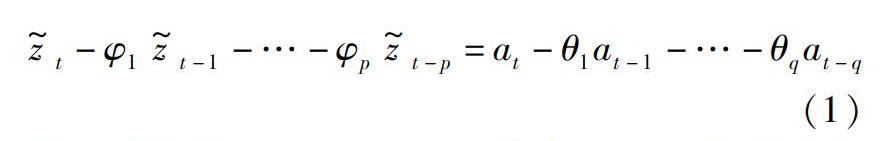
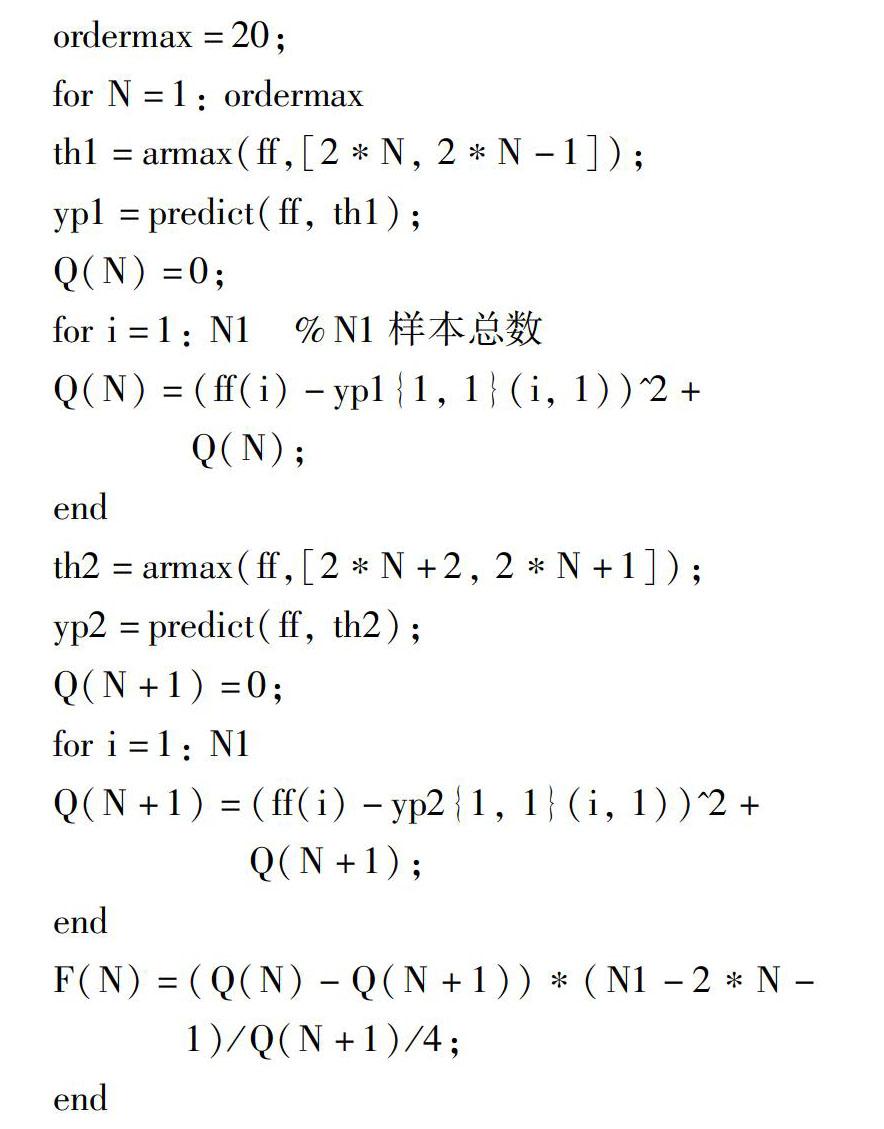
摘 要：制导炸弹自动化测试是减少测试人员负担、 降低研发成本、 提高测试效率的重要手段。 测试数据的判读是自动测试系统的重要组成部分。 传统测试数据判读方法效率低下， 难以应对制导炸弹大量测试数据的分析判读需求。 针对这一问题， 本文利用MATLAB软件， 完成了制导炸弹测试数据时间序列判读方法设计， 并通过对舵机角度反馈偏差数据的判读， 对该方法进行了工程验证。 验证结果显示， 设计的时间序列判读方法能在先验数据集基础上， 对测试数据进行异常检测， 提高了测试数据的判读效率和准确性。

关键词： 制导炸弹; 时间序列; 数据判读; 测试

中图分类号： TJ414文献标识码： A 文章编号： 1673-5048（2018）05-0073-06[SQ0]

0 引言

制导炸弹的测试工作贯穿于其研制、 试验、 生产、 使用等各个阶段， 产生了大量的测试数据。 通过对这些测试数据的判读， 测试人员能够了解到炸弹各个部件的工作状态， 并能进行异常的诊断。

目前， 对测试数据的判读多停留在依靠测试人员经验比较、 图像趋势观察阶段， 效率低下。 采用自动测试技术和先进的数据判读方法， 提高测试数据判读的实时性、 准确性和工作效率， 减轻测试人员工作负担， 是测试工作的迫切需求[1-4]。

国内不少学者对测试数据判读方法进行了研究。 吴限德等运用時间序列分析方法， 实现了对小卫星测试数据的在线判读[1]。 曹永梅等针对卫星控制系统测试数据， 基于设置的判读规则方法， 设计了测试数据自动判读系统[2]。 汪洋等对卫星测试系统测试数据的变化规律进行了研究， 研制了一种开放的判读函数编译平台[3]。 苏振华等利用卫星下传的测试数据， 提出了一种基于BP神经网络的卫星故障诊断方法[4]。 在这些已应用的方法中， 时间序列分析方法可以简单高效地建立数据数学模型， 能够近似描述各种类型的数据， 达到预测数据发展趋势并诊断异常的目的， 在各个领域都得到了广泛的应用[5]。

制导炸弹的测试数据具有数据量大、 数据随环境影响大、 数据类型复杂多样等特点。 本文运用时间序列分析理论， 借助MATLAB软件工具， 对制导炸弹测试数据进行了判读， 完成了测试数据判读方法的研究及应用验证。

1 时间序列分析理论

1.1 ARMA模型的基本原理

时间序列模型包括自回归模型（AR模型）、 滑动平均模型（MA模型）、 自回归-滑动平均模型（ARMA模型）等。 其中ARMA模型中既包含自回归部分也包含滑动平均部分， 这使模型在拟合数据时具有很大的灵活性[6]。 其表达式为

z～t-φ1z～t-1-…-φpz～t-p=at-θ1at-1-…-θqat-q（1）

式（1）简记为ARMA（p， q）。 其中： p和q分别为自回归部分和滑动平均部分的阶数;φi（i=1， 2， …， p）和θi（i=1， 2， …， q）分别为自回归和滑动平均系数。特殊的， 若p=0， 则模型退化为MA（q）; 若q=0， 则模型退化为AR（p）。

模型类型可以通过数据的自相关函数（ACF）和偏相关函数（PACF）的拖尾性、 截尾性与模型类别的关系来判读， 模型识别关系如表1所示[7]。

1.2 DDS建模方法

DDS（Dynamic Data System）方法是Pandit-Wu在1977年研究连续系统和离散系统的对应关系时提出的[8]。 他们经过研究发现， 线性定常系统在白噪声作用下的响应， 经过均匀间隔采样所得到的时间序列， 总可以用离散的ARMA（n， n-1）模型来拟合[6]。

根据制导炸弹测试数据量大、 变化剧烈、 环境影响大等特点， 本文选用DDS方法来建立测试数据的时间序列模型。 DDS建模方法的一般流程如图1所示[6]。

1.3 模型阶数的确定

时间序列模型阶数确定常用的方法有偏相关定阶法、 白度检验定阶法、 F检验法、 AIC、 BIC、 FPE准则定阶法等。 DDS建模方法选用F检验法来检测模型阶数。 F值计算公式为[7]

F=Q1-Q02Q0N-p-q～F（2， N-p-q）（2）

式中： Q0为模型ARMA（p， q）的残差平方和;Q1为模型ARMA（p-1， q-1）的残差平方和; N为样本长度;p和q分别为自回归和滑动平均的阶数;2是被检验的阶数差数。 如果F>Fα， 则假设不成立， 模型阶数仍有上升的可能。 否则ARMA（p-1， q-1）是合适的模型。 Fα从F分布表中查得。

2 基于MATLAB软件工具的时间序列建模

2.1 MATLAB时间序列函数

MATLAB时间序列处理函数主要放在控制类工具箱的系统辨识工具箱中[8]。 涉及时间序列分析的部分函数如表2所示。

armaxm=armax（data， [na， nc]）对于时间序列data是时间序列， na和nc分别是时间序列自回归和滑动平均的阶数

predictyp=predict（m， data）按照模型m， 根据数据data， 进行数据预测计算， 预测数据保存在yp中[9]

residresid（m， data）计算置信度为99%的模型残差图[10]

2.2 MATLAB时间序列建模步骤

本文根据DDS建模过程， 运用MATLAB工具， 建立时间序列模型的步骤如下：

（1） 导入原始数据， 新建原始数据矩阵。

（2） 使用detrend函数对原始数据进行平稳化和零均值化处理。

（3） 运用相关分析函数autocorr和parcorr得到自相关和偏相关函数图， 判断时间序列属于哪种典型模型， 进而对通过DDS建模方法得到的时间序列模型进行验证。

（4） 运用armax函数编写程序， 建立各个阶次的时间序列数学模型。

（5） 运用编写程序计算F值进行F检验， 计算预测数据残差平方和作模型评价参考。

（6） 使用predict函数进行预测数据计算， 并与原数据进行比较， 检查模型拟合情况。

（7） 运用resid函数对预测数据进行残差分析， 对残差序列进行白噪声检验计算， 验证数学模型和原数据的拟合情况[11]。

（8） 根据测试数据时间序列的模型阶次、 模型参数、 残差方差等能表征系统特性的参数情况， 与正常样本的数据对比， 对测试数据异常情况进行分析判断。

3 舵机转角反馈偏差数据判读

3.1 时间序列模型识别

制导炸弹舵机转角反馈偏差数据是舵机控制转角和舵机实际转角反馈值之间的差值， 是随时间动态变化的时间序列， 偏差幅度大小受舵机调整剧烈程度等因素影响， 是反映舵机跟随控制系统命令情况的重要指标， 对测试舵机是否存在异常具有重要意义。 某次测试舵机转角反馈偏差原始数据如图2所示。

舵机转角偏差数据经detrend函数预处理后为平稳零均值时间序列， 用autocorr， parcorr计算的ACF和PACF图如图3～4所示。 由图可以看出两者均为拖尾的， 因此选用ARMA模型来拟合。

3.2 建立数学模型

3.2.1 初步建立模型并进行F检验

根据DDS建模步骤， 用armax函数， 依次建立ARMA（2， 1）及ARMA（2n+2， 2n+1）模型， 并进行F检验。 计算得到的F值如表3所示， 由表中可以看出在ARMA（28， 27）处时， F<Fα=2.37。

3.2.2 对经典DDS建模流程的修改

为找到适合模型， 本文实际按照图5所示的流程图进行数据建模。

图1中流程图要求对模型参数φ2n，θ2n-1的置信区间进行是否包含零的判断。 实际建模过程中发现计算φ2n，θ2n-1的置信区间是困难的， 且DDS方法的流程最后步骤要求设定“其他模型”进行检验， 确定最终模型。 而ARMA（2n-1， m）， m≤2n-2模型和ARMA（2n， m）， m≤2n-1模型就是很好的“其他模型”。

因此， 首先用相关性分析判断模型类型， 以便对DDS建模方法得到的模型进行验证。 当使用DDS方法得到ARMA（2n， 2n-1）模型后， 直接对上述两模型进行建模和F检验。 这样虽然增加了计算量， 但可以避免错漏适合模型。 以现代计算机的速度和MATLAB算法的高效率， 增加的计算时间实际证明是很少的。

时间序列建模和F检验的部分MATLAB程序如下：

3.2.3 修改的DDS建模步骤应用结果

继续建立ARMA（27， 26），ARMA（27， 25），ARMA（28， 26），ARMA（28， 25）等模型并与ARMA（28， 27）进行F检验比较。 计算得到的F值如表4所示。 可见ARMA（28， 27）是合适模型。

3.3 测试数据模型分析

图6显示了残差序列自相关系数图， 根据白度检验定阶法计算得到χ2k，α =34.38， Qk =29.89（显著水平为α=0.01， k=25）， χk，α >Qk即残差序列是白噪声。 图7为反馈差值预测值与原始值拟合图，可以看出预测模型能很好地拟合实际数据[12]， 验证了预测模型和建模方法的有效性。

利用此方法对四枚制导炸弹实验测试的16组舵机转角偏差测试数据进行时间序列建模， 得到的数据计算结果见表5。

从表5计算结果可见， 同一炸弹四个舵机的转角偏差平方和、 方差、 模型阶次均相差不大， 而不同炸弹的数据相差较大。 这主要是由于不同炸弹工作工况不同导致的， 符合经验预期。

在表5中， B弹第3通道舵机数据的时间序列模型阶次（28， 27）， 与其他舵机测试数据的阶次小于10的情况相差较大， 因此初步判断此舵机跟随性能与其他舵机相比存在异常。 经人工查看舵机偏差数据图像发现， 此舵机在刚上电时段跟随偏差较大， 将此段数据删除后重新建模分析， 计算的模型阶次为（7， 6）， 继续删除相同长度的数据序列继续建模， 得到的模型阶次依次为（4， 3）， （6， 5）， （8， 7）， 与其他通道相差不大。 这说明偏差数据时间序列模型阶次的大小与舵机跟随偏差较大数据存在一定的相关性。

表5中的B弹1通道模型阶次（3， 2）、 C弹2通道模型阶次（5， 4）、 D弹1通道模型阶次（9， 8）、 D弹4通道模型阶次（6， 4）均是通过验证模型ARMA（2n-1， m）， m≤2n-2和ARMA（2n， m）， m≤2n-1得到的拟合模型阶次， 这些结果说明了改进DDS建模流程在实际建模过程中的有效性。

4 总结

本文针对制导炸弹测试数据自动判读的需求， 运用时间序列分析理论， 借助MATLAB软件工具， 建立了测试数据的时序数学模型， 对测试数据进行了异常分析， 形成了包括判读理论、 判读实施工具和判读结果分析的判读方法。 實际判读过程表明， 该方法能够对制导炸弹异常数据是否存在异常进行对比判读， 提高了制导炸弹测试数据判读的效率和可靠性， 改变了以往仅能依靠数据趋势图和测试人员经验判读数据的现状， 为数据自动判读系统的设计打下基础。

本文在实际运用DDS方法进行建模过程中， 对DDS建模经典流程进行改进， 使其更便于使用计算机及数值分析工具软件建模。 此修改流程可为今后运用DDS方法建模提供参考。

参考文献：

[1] 吴限德， 孙兆伟， 陈卫东. 小卫星测试数据在线时间序列判读方法[J]. 哈尔滨工程大学学报， 2012， 33（3）：383-388.

Wu Xiande， Sun Zhaowei， Chen Weidong. An On Line Data Interpretation Method in a Micro Satellite Ground Test System Based on a Time Series Analysis[J].Journal of Harbin Engineering University， 2012， 33（3）：383-388.（in Chinese）

[2] 曹永梅， 周剑敏， 潘立鑫. 卫星控制系统测试数据自动判读系统的设计与实现[J]. 空间控制技术与应用， 2013， 39（5）： 58-62.

Cao Yongmei， Zhou Jianmin， Pan Lixin. Design and Implementation of Automatic Data Discrimination System for Satellite Control System[J]. Aerospace Control and Application， 2013， 39（5）： 58-62.（in Chinese）

[3] 汪洋， 徐犇， 曾齐， 等. 基于函数解析的卫星测试数据自动判读[J]. 遥测遥控， 2016， 37（1）：38-44.

Wang Yang， Xu Ben， Zeng Qi， et al. Automatic Interpretation of Satellite Test Data Based on Analytic Function [J]. Journal of Telemetry， Tracking and Command， 2016， 37（1）：38-44.（in Chinese）

[4] 苏振华， 陆文高， 奇晶， 等. 基于BP神经网络的卫星故障诊断方法[J]. 计算机测量与控制， 2016， 24（5）：63-66.

Su Zhenhua， Lu Wengao， Qi Jing， et al. A Method of Satellite Fault Diagnosis Based on BP Neural Network[J]. Computer Measurement & Control， 2016， 24（5）：63-66.（in Chinese）

[5] 吴怀宇. 时间序列分析与综合[M]. 武汉：武汉大学出版社， 2004.

Wu Huaiyu. Time Series Analysis and Applications [M]. Wuhan：Wuhan University Press， 2004.（in Chinese）

[6] 张树京， 齐立心. 时间序列分析简明教程[M]. 北京：清华大学出版社， 北方交通大学出版社， 2003.

Zhang Shujing， Qi Lixin. Time Series Analysis Plain Course[M]. Beijing： Tsinghua University Press，Northern Jiaotong University Press， 2003.（in Chinese）

[7] 周世琼， 康龙云， 张彦宁， 等.基于MATLAB系统辨识工具箱的风信号预测[J]. 太阳能学报， 2008， 29（4）：417-421.

Zhou Shiqiong， Kang Longyun， Zhang Yanning， et al. Wind Signal Forecasting Based on System Identification Toolbox of MATLAB[J]. Acta Energiae Solaris Sinica， 2008， 29（4）：417-421.（in Chinese）

[8] 栾颖. MATLAB R2013a工程分析与仿真[M]. 北京：清华大学出版社， 2014.

Luan Ying. MATLAB R2013a Engineering Analysis and Simulation[M]. Beijing：Tsinghua University Press， 2014.（in Chinese）

[9] 邵璠， 孙育河， 梁岚珍. 基于时间序列法的风电场风速预测研究[J]. 华东电力， 2008， 36（7）：26-29.

Shao Fan， Sun Yuhe， Liang Lanzhen. Study on the Time Series Wind Speed Forecasting of the Wind Farm Based on Time Series[J]. East China Electric Power， 2008， 36（7）：26-29.（in Chinese）

[10] 韩路跃， 杜行检. 基于MATLAB的时间序列建模与预测[J]. 计算机仿真， 2005， 22（4）：105-107， 182.

Han Luyue， Du Xingjian. Modeling and Prediction of Time Series Based on MATLAB[J].Computer Simulation， 2005， 22（4）： 105-107， 182.（in Chinese）

[11] 林卉. 非平穩时间序列的建模方法研究[D].武汉：武汉理工大学， 2005.

Lin Hui. A Modeling Method Research on Nonstationary Time Series[D]. Wuhan：Wuhan University of Techno logy， 2005.（in Chinese）

[12] 柴嘉薪， 王新龍， 王盾， 等. 一种光纤陀螺随机振动误差高精度建模方法[J]. 航空兵器， 2017（4）： 49-54.

Chai Jiaxin， Wang Xinlong， Wang Dun， et al. A High Precision Modeling Method for Random Vibration Error of Fiber Optic Gyroscope[J]. Aero Weaponry， 2017（4）： 49-54.（in Chinese）

Application of Time Series Analysis in the

Guided Bomb Test Data Interpretation

Zhang Rui， Liu Huaixun，Wei Zhigang

（China Airborne Missile Academy， Luoyang 471009， China）

Abstract：Automatic test of guided bomb is an important means of reducingoperators workload， reducing development costs， improving test efficiency. Data interpretation is one of the most important partsof automatictest systems. Traditional data interpretations have a low efficiency， therefore， it is difficult to satisfy the requirement of test systems with a large number of test data. To solve this problem， thetime series interpretation method of guided bomb test data is obtained using MATLAB software. Taking advantage of the steering engine angle feedback deviation data， the proposed method is verified. The results show that the interpretation method can detect data abnormalities comprehensively based on a prior data set， thereby improving the accuracy and efficiency of the test data.

Key words：guided bomb; time series; data interpretation; testing