浅析初中数学探究式课堂教学

胡丽明

新课标下的探究式教学在提高学生自主学习的能力和提高中学教学质量及教学效率方面都发挥了积极的作用，但探究式教学仍然处在初步探索的阶段，在具体的教学过程依然存在着困境和难题。

一、在初中数学的探究式教学中要坚持基础性原则和拓展性原则

基础性原则指初中数学的探究式教学要以教材中的基础性知识为探究内容，制定自主学习目标是要重视学生对数学概念、计算方式、几何图形的理解和感知，指导学生自主总结出基本概念、定理与计算法则之间的关系，在学生的脑海中形成完整的知识体系.拓展性原则指在掌握数学知识的基础之上关注学生的数学思维和数学认知的提升，这也是素质教育的本质要求。探究式教学既是一种学习方式，也是一种学习过程。笔者运用探究式教学法教学《树的高度》，通过设置情境，以开放式问题为引线，引导学生对不同测量方案进行探究。

1.创设情境、提出问题。情境：打开多媒体播放器，音乐声中，屏幕上出现了一位小学生蹦蹦跳跳上学，路边有一棵大树，画外音响起：你能帮助她想出一种测量方案吗？请说明你的方法。

2.学生独立思考，自主探究性。课堂内非常安静，教师不时给学生以启发。7分钟后，绝大多数学生都找到了至少一种测量方案，让他们把想法与组员交流，相互評价，然后参与学生的讨论中。

3.探究辩析，解决问题。此阶段采取谁设计的方案由谁主讲，大家共同参与讨论的方式。

生1：如图1，自己身高CD=b，在地面上任意选取一点D，测出树顶仰角α，再测出D到树底部距离DB，可求出树高：

AB=b+DBtanα

生2：可以利用平面镜测树高，在地面处放一面镜，后退到恰能从镜中看到树的顶端为止，这时只要测出DO和OB，还有自己的身高CD，就可以求出树高：

AB=OB·CD/OD（如图2）

生3：如果你身边没有小镜子，也可以找一个盛水的工具，盛满水代替平面镜同样能测树高。

生4：我有办法解决他的问题。如图3，我们可以利用太阳光线测树高，先测出小女孩的身高CD和影长DE，再测出树的影长BF，利用在同一时刻，高度和影长成正比，可求出树高：AB=CD·BF/DE

生5：（起来反驳）如果要是阴天没有阳光，地面上没有树影，他的办法就行不通了。一语惊醒梦中人，同学们个个点头称是。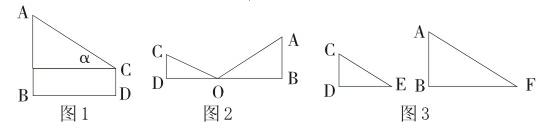

生6：（健步走上讲台，把一张他和一棵大树的合影放在投影仪上）这是一张外出旅游时的照片，我只要量出照片中自己的高度和树的高度，再测出自己的实际的身高，利用相似就可以求出照片中树的实际高度。

4.拓展问题。当学生们沉浸在成功的喜悦中，老师再设疑启发：在上述问题中，同学们运用了哪些数学知识？学生们很快答出：①运用了想似三角形的知识，如平面镜法、影长法等；②解直角三角形。

师：在这道题中，树的底部可以直接到达。那么，在生活中你见过的树是不是底部都可以到达呢？

生：不是。

师：那么，你们还见过哪些环境中的树底部不可以到达？它的高度又如何测量呢？

生：学生们兴奋地说着：“山上的树、河边的树、湖心岛上的树……”

师：在这些情境中，你还能用上述的办法测量树高吗？

这时，师点击电脑，伴着潺潺流水声，飞出一副“江边垂柳”的风景画，画外音响起：站在江边看江对岸的柳，它的高度如何测量，你能想出测量方案吗，请你画图说明？学生独立探究后先在小组内交流，最后班级交流。

生：如图4所示，在河这一岸取两点AB，使AB和树底部在同一直线上，至B处，再测树顶仰角α，测出身高AC=a，后退距离AB=b，则得树高：EF=AB/（1/ tanβ—1/tanα）+AC

5.布置作业，发展能力。留心观察生活中的高度测量问题，是否会有什么新的发现？

学生通过探究积极参与教学过程，激发他们的学习主动性，促进他们的思维活动，开发了他们的智力，最大限度地挖掘他们自身创造潜力，使他们具有创新精神和创造力，成为符合时代潮流的人才。？（作者单位：江西省南昌市第二中学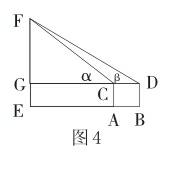）endprint