高考三视图问题常考题型及处理策略

☉华中师范大学第一附属中学 程季康

三视图问题是立体几何的入门内容，也是高考数学中的一个重要考点.翻阅近年来的高考试卷，三视图问题是高考的必考内容；在学习之余，结合近年的高考真题，我总结近年来高考对三视图的考查主要有以下几个方面，现分类例析，供参考：

一、判断几何体的三视图问题

给出一个几何体的直观图，然后根据几何体的形状判断其三视图的问题.由于其难度较小，因此这类直接判断型问题高考基本没有涉及过.但在2013年和2014年的高考中，曾以空间直角坐标系中点的坐标来表示几何体，利用考生的想象能力来判断几何体的三视图的问题.

例1（2014年湖北卷）在如图1所示的空间直角坐标系O-xyz中，一个四面体的顶点坐标分别是（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出编号为①②③④的四个图，则该四面体的正视图和俯视图分别为（ ）.

图1

（A）①和② （B）③和①

（C）④和③ （D）④和②

解析：如图2，将四面体放入正方体中，四面体ABCD即坐标系中四个点所围成的四面体，显然可以看出其正视图为④，俯视图为②，故选D.

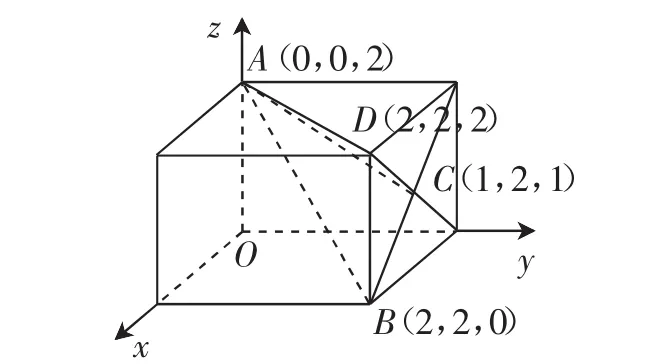
图2

例2（2013年全国卷Ⅱ）一个四面体的顶点在空间直 角 坐 标 系 中 的 坐 标 分 别 是 （1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以平面为投影面，则得到正视图可以为（ ）.

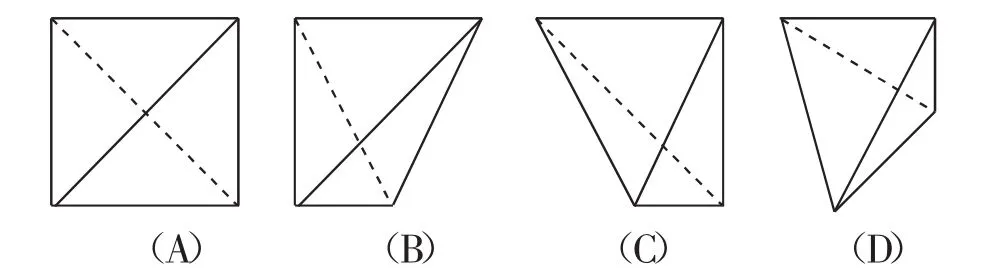
解析：在空间直角坐标系中，根据点的坐标先画出四面体O-ABC的直观图，再以zOx平面为投影面，沿y轴负半轴方向看去则得到正视图，如图3可以观察得到A符合要求，故选A.

图3

点评：上述两题给出的均是空间直角坐标系中点的坐标，直接由点的坐标想象出空间几何体的形状，然后再判断其三视图，理论上是可以，但实际操作难度较大；此时将该几何体在空间直角坐标系中还原，则判断其三视图的问题即可迎刃而解.

二、利用几何体的三视图还原几何体并计算

纵观近年来的高考试题，大多数试题是先给出几何体的三视图，要求计算几何体的体积、表面积及其他量.其中以计算几何体的体积的问题居多，其次是计算几何体的表面积，有时也会要求计算棱长或其余与几何体有关的量.

1.利用几何体的三视图计算几何体的体积

例3（2017年北京卷）某三棱锥的三视图如图4所示，则该三棱锥的体积为（ ）.

（A）60 （B）30 （C）20 （D）10

图4

图5

解析：根据几何体的三视图，还原其直观图，如图5，可以看出该几何体底面三角形两条直角边长为3和5，高为4，其体积为

点评：对于空间几何体的三视图问题，一般首先要观察几何体的三视图，找出其特征及数量关系，再还原该几何体的直观图；在还原几何体的直观图时，对于规则的几何图形，一般将其放到长方体中来观察特征，进行还原，最后根据还原后的图形计算几何体中边角关系.需要注意的是本题中俯视图中的图形不是几何体的底面，它只是俯视时看到的图形而已.

例4（2017年全国卷Ⅱ）如图6，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）.

（A）90π （B）63π

（C）42π （D）36π

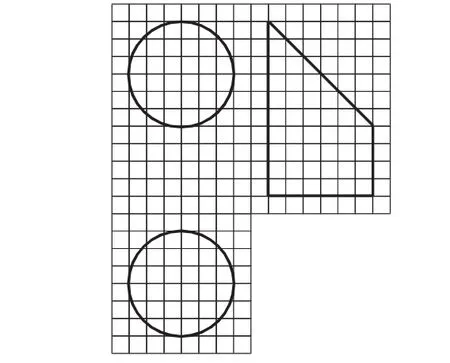
图6

解析：由网格纸上的小正方形边长为1可以看出该几何体的正视图由一个边长为6的正方形和一个直径为6的半圆组成，其侧视图由一个长为6，宽为4的长方形和一个直角边长为6的等腰直角三角形组成，其俯视图是一个直径为6的圆；因此该几何体的下半部分是一个底面半径为3，高为4的圆柱；上面部分是一个底面半径为3，高为6的圆柱切去一半所得的部分.所以其体积为.故选B.

例5（2015年课标全国卷Ⅱ）一个正方体被一个平面截去一部分后，剩余部分的三视图如图7所示，则截去部分体积与剩余部分体积的比值为（ ）.

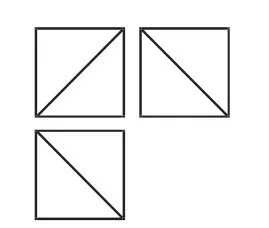
图7

图8

解析：根据题意，该几何体是由一个正方体截去部分后剩下的图形，由该几何体的三视图还原其直观图得到正方体ABCD-A1B1C1D1截去了一个三棱锥A-A1B1D1后的图形如图8所示.易知

点评：在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线.在还原空间几何体实际形状时，一般以正视图和俯视图为主，结合侧视图进行综合考虑.求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解.

2.利用几何体的三视图计算几何体的表面积

例6（2017年全国卷Ⅰ）某多面体的三视图如图9所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ）.

（A）10 （B）12 （C）14 （D）16

图9

图10

解析：根据该几何体的三视图可以看出该几何体是一个三棱锥叠放在一个三棱柱上面形成的，其直观图如图10所示，从直观图可以看出该几何体有2个全等的梯形，其上底为2，下底为4，高为2，所以其面积之和为S=2×12.故选B.

点评：对于根据几何体的三视图计算几何体的表面积问题，一般先要根据几何体的三视图还原其直观图，再根据直观图观察该几何体各个面的形状，从而计算其表面积.

自2007年以来，埃塞通过国际竹藤组织的竹子项目引进了约20多个竹种试种，大多数竹种表现良好，其中龙竹(Dendrocalamus giganteus)、马来甜龙竹(D.asper)、版纳甜龙竹(D.hamiltonii)、黄竹(D.membranaceus)和龙头竹(Bambusa vulgaris)建议大规模种植。

例7（2016年全国卷Ⅲ）如图11，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（ ）.

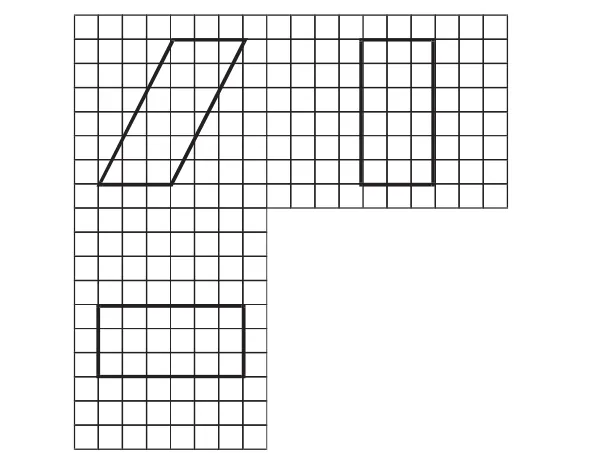
图11

解析：根据三视图，可以看出该几何体是一个斜四棱柱，其底面是一个边长为3的正方形，高为6；其正视图看到的平行四边形即为该几何体的前面，显然其是一个平行四边形，底为3，高为6，面积为S1=3×6=18；其上下两个面是两个边长为3的正方形，每一个面的面积为S2=3×3=9；其左右两个面是两个竖着放的长方形，底为3，高为正视图中平行四边形的一个边长度为，即每一个侧面的面积为.综上，该几何体的表面积为S=2（S1+S2+S3）=54+18.故选B.

点评：本题将三视图放在网格中，其目的就是给出计算所需要的边的长度.本题中几何体的前后两个面和上下两个面很直观，与其正视图及俯视图类似，但左右两个侧面是两个竖放的长方形，其高线的长需要引起注意，防止出错.

3.利用几何体的三视图计算几何体中棱长或球体的半径

例8（2017年北京卷）某四棱锥的三视图如图12所示，则该四棱锥的最长棱的长度为（ ）.

图12

图13

解析：根据该几何体的三视图，还原该几何体如图13所示，可以看出该几何体是边长为2的正方体中所截得到部分，其底面是边长为2的正方形，顶点垂直于底面.显然其最长棱为图中棱PA，其长度为|PA|=.故选B.

点评：本题考查空间几何体三视图的识别及几何体边角的计算，首先要根据其三视图还原其直观图，再从其直观图中判断出其中最长的边，最后根据给出的数值进行计算.

例9（2015年全国卷Ⅰ）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图14所示.若该几何体的表面积为16+20π，则r=（ ）.

（A）1 （B）2 （C）4 （D）8

图14

解析：由三视图可知，此组合体的前半部分是一个底面半径为r，高为2r的半圆柱（水平放置），后半部分是一个半径为r的半球，其中半圆柱的一个底面与半球的半个圆面重合，所以此几何体的表面积为2πr2=4r2+5πr2=16+20π，解得r=2.故选B.

点评：本题只给出了三视图中的两部分，解决的关键仍然是从正视图及俯视图中确定几何体的形状.从正视图是个圆可以确定该圆柱是横放，从俯视图中的长方形和半圆型可以确定半球在圆柱的后面，从而利用圆柱和球体的表面积公式计算出球的半径.

4.利用几何体的三视图既计算体积又计算表面积

例10（2016年全国卷Ⅰ）如图15，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是，则它的表面积是（ ）.

图15

（A）17π （B）18π （C）20π （D）28π

点评：本题解题的突破口在由三视图观察出几何体的形状，从而根据体积的值计算出球体半径的长度，最终计算出球体的表面积.

例11（2016年浙江卷）某几何体的三视图如图16所示（单位：cm），则该几何体的表面积是______cm2，体积是_____cm3.

图16

图17

解析：根据三视图，可以发现该几何体是两个相同的长方体靠在一起而形成的，它们的底面是边长为2的正方形，高是4，其中一个“站立”，另一个“平躺”.其直观图如图17所示.所以其表面积为S=2×（2×2×2+2×4×4）-2×2×2=72（cm2），体积为V=2×2×2×4=32（cm3）.

点评：本题考查三视图的识别与几何体的表面积与体积的计算.先根据三视图还原几何体的直观图，再计算其表面积与体积.

从上面近年来的高考真题可以看出，三视图问题往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由几何体的三视图准确确定几何体的形状及其结构特征，然后再根据要求进行计算.一般说来，其难点主要有两点：一是根据三视图确定几何体的形状及相关数量关系；二是根据相关数量关系准确进行计算.只要解决了这两个难点，三视图问题一般都能迎刃而解.