反思解题方法，提升思维灵活性——以反思三角函数解题方法为例

☉江苏省常熟市梅李高级中学 朱利锋

我们在数学教学中常常会遇到这样的现象，学生课堂上表现还行，但是到了课后作业时问题重重，考试如果题目情境比较新学生解决问题的能力就变得很弱，错误连篇，为什么会出现这样的现象？笔者认为这是学生数学思维不灵活的表现，思维定式严重，因为学生不注重反思，在问题解决后思考问题仅仅停留在题干和自己解决问题的方法表面，缺乏对问题整体上的思考与把握，如果我们在学生问题解决后及时地引导学生反思，换一个视角对问题进行新的思考，不仅仅可以发展学生的全局意识，还能够引导学生多角度挖掘解决数学问题的方法，同时比较多种方法的优劣，与此同时学生的思维也在反思解题的过程中变得更为灵活.本文以三角函数中的求值与证明为例就该话题进行分析.

一、课堂上“案例法”领引学生反思

学生反思意识与反思能力是需要我们教师去引领与培养的，选择合适的例题并指引学生在解题后进行必要的反思有助于数学方法的沉淀和解决数学问题能力的有效提升.

例1 已知tan（α+β）=mtan（α-β），且m≠1，求证：

反思：例1的题眼在哪里？你选择的方法是什么？有没有其他的方法可以证明？

在上述几个方面的引导下，学生很自然地回顾自己的解题过程与方法，观察、比较已知条件与证明目标之间角度存在的差异，然后通过角度变换进行求解的，在这一方法清晰后，学生思维切向“有没有其他办法呢？”的反思之中，通过反思和交流学生可以找到新的方法：

另法1：“化弦法”，学生通过对比已知式与证明目标，从函数名出发，将已知式变形为的右边，进一步整理即可获得，紧接着“切化弦”即可.

实践经验表明，学生通过上述解题后反思过程，能够有效提升审题能力和信息加工能力.

分析常规解法：例2对于学生而言，容易想到的方法：从待求式出发，将求解的问题化为求解sinα，cosα，如何求sinα，cosα呢？很自然地联系到借助于“解方程组”这一最基本的方法将得，再结合sin2α+cos2α=1解得sinα，cosα，然后再借助于二倍角公式求出sin2α，cos2α，最后代入cos中求解.这个方法很常规，学生也很容易就能想到，不过对于计算能力较弱的学生而言，在求解二元二次方程组时可能会因为过程稍微烦琐而出错，因此，我们可以引导学生从是否有其他解法的视角进行解题后反思.

从这两个例题的处理来看，两个案例均在学生完成了问题解决后引导学生反思题目条件与待求目标之间的关系，寻求解题的其他途径与方法，这样的反思引导着学生思维发散出去，从题干中所给信息的各个不同角度去思考可利用的数学思想方法，尝试着运用不同的数学方法完成问题的解决，在运用方法解决问题的同时也存在着对解法优劣的比较，学生的解题思路得以有效拓展，促进了知识在大脑中的有益联系，让学生应用数学解决问题的思维变得更具灵活性.

二、精心设计课后作业，促进知识内化

学生的反思意识和能力在课堂例题的处理中已经形成并得到了一定的发展，但是不同的学生可能发展的程度不一样，为此我们为了检测学生的学习成果，同时也是为了帮助学生及时地调整学习的方向与节奏，我们课后的作业布置应该与课堂上所用的方法相匹配.例如，在和学生课堂上处理了上文中的两道例题后，笔者精心设计有针对性的作业，旨在及时地反馈学生的学习状况.

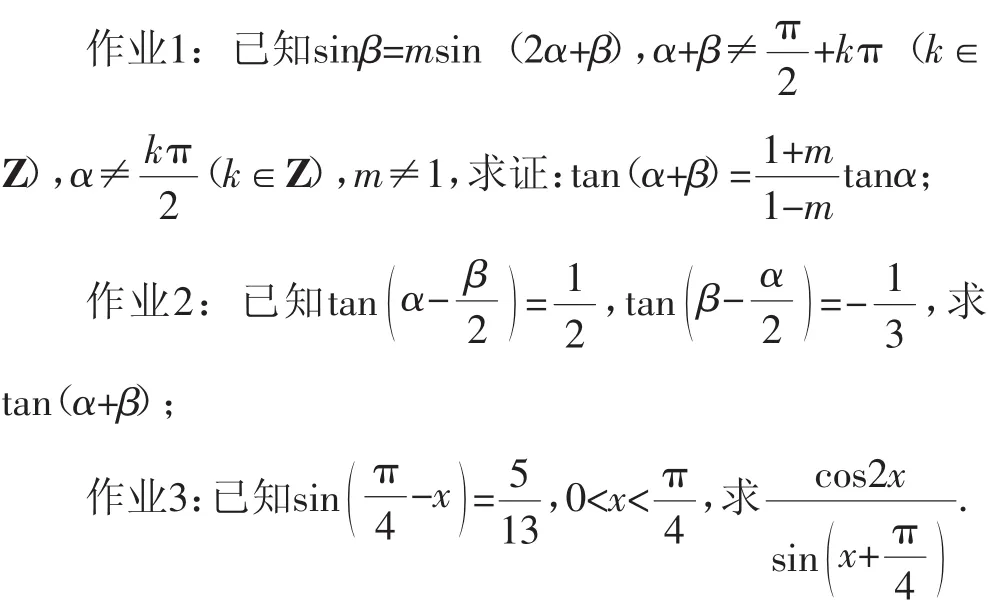
设计意图：这三个作业的设置与课堂上的两道例题紧密联系，作业1与例1相联系，在例1的问题解决中学生已经观察并分析了角度差异、函数名称差异、已知式与目标式的结构差异，当时问题解决的方法与经验可以迁移并运用到作业1的问题解决中来；作业2与例2相联系，在例2的反思中学生已经意识到了“角的拼凑法”在问题解决中的重要性，通过作业2让学生进一步应用，反馈学生在相似问题的解决中是否能够做到触类旁通；作业3与例题2中解决问题的多种方法相联系，但是对学生信息加工能力的要求要比作业2要高一些，能够很好地反馈学生思维的灵活性.总体而言，这3个作业的难度依次增加，但只要学生能够很好地将课堂所学迁移过来，问题是可以解决的，那么学生的完成情况如何呢？

结果反馈：作业1仅有一个同学粗心做错，其他同学在问题的解决中所用的方法不完全相同，有部分同学运用的是“弦化切”，有部分同学运用的是“切化弦”，不过均成果解题；作业2有2个同学做错，同样在做对的学生中方法也各异，有部分同学是先借助于二倍角公式和α），然后再拼凑角α+β=（2α-β）+（2β-α），求出tan（α+β），也有部分同学选择的是先拼凑角先求，然后再借助于二倍角公式求tan（α+β）.不管是作业1，还是作业2，学生在方法的应用上都很成功和灵活，说明我们课堂上的反思环节起到了一定的效果，学生的思维发散开来，并成功的运用到了数学问题的解决中来.相对较难一点的作业3，错误率也相对高一些，有9个同学出错，对于这几个同学出错的原因在哪里呢？笔者选择追问的方式引导这部分学生从失败中走出来.

三、访谈式纠错，领引学生再反思

错误并不可怕，如果我们教师处理得好，不仅可以领引学生从错误中走出来，还有利于学生反思能力和思维灵活性的进一步提升.

例如，面对作业3，9个同学做错了的结果，为了帮助学生从失败中走出，有效衔接原有思维，笔者随机选择了一个作业3出错的学生进行访谈.

师：在解决“作业3”时，你用到了哪些方法？你回忆一下困难出现在哪里？

生：用了角的拼凑法、解方程组等等；这些方法都试过了，解方程组的方法我已知道原因了，是因为计算错误.但是角的拼凑不是很顺利，由2x时出现了困难.

师：说说你具体的拼凑过程吧.

生（顿悟）：哦，我明白了.

通过这样一个简单的对话式的访谈，引导学困生自己发现问题并解决问题，有助于增强他们的自信心，提升他们思维的灵活性.