算用结合学以致用

杨凯明

【摘要】“算用结合”是义务教育数学新课程改革的教学理念之一，也是新教材编排的最明显的特点。随着课程改革的深入，在计算教学中，借助“算用结合”的方式已经成为广大数学教师的共识。因此，在引导时，需要结合具体的问题情境，然后引导学生在观察与比较中去发现算理，逐步揭示算法，对各种不同的算法进行评判、思考，理解法则规定的合理性。

【关键词】算用结合 混合运算 解决问题

一、教前思考

在很多教师的观念中，四则混合运算是一种规定，是没有什么道理可以讲的，所以运算顺序可以当然的以“告诉”的方式让学生接受。有些好奇心强的孩子问为什么，也会被老师“这是规定”搪塞过去。让学生探究明白“先乘除后加减”的“算理”不是一件容易的事。

“乘加混合运算”是北师大版小学数学三年级上册的教学内容。本节课中，把数学知识寓于现实的、有意义的学习活动中，将学生通过对“1个蛋糕和4个面包共要多少钱”这个问题作为教学的起点，引入“乘加混合运算”的教学。根据教材的要求和学生的实际，确定如下三个教学目标：经历解决“小熊购物”问题的探索过程，感受画图策略的意义和价值，体会混合运算中“先算乘法，再算加法”的合理性；能运用“先算乘法，再算加法”的运算顺序正确地进行计算；可以初步地尝试借助直观图表示乘加等实际问题的数量关系，提高分析和解决问题的能力。根据这样的教学目标和学生学习过程中的行为预设的研究，本节课的教学重点是在解决问题的过程中，体验“先算乘法，再算加法”的合理性及正确的计算。基于以上分析，教学过程的设计要充分考虑学生的生活经验，选取学生熟悉的生活化的素材作为教学内容，创设亲切、自然、有效的与学生生活密切相关的教学情境，让学生积极主动地参与知识的形成过程，引导学生在生活情境中体验与感悟数学，体现数学学习的价值。本节课采用的基本流程是：激发冲突——创设情境——尝试探究——观察比较——解释应用——知识建构——解决问题。

二、教学过程

（一）复习导入，引发冲突

1.出示第一、二组口算题

（1）6+3-4 （2）6÷3×4

6-3+4 6×4÷3

（学生纷纷举手，气氛热烈，学生马上报出得数）

师：你是怎么算的？（指第一组算式）

生：先算6加上3等于9，再算9减去4得5。

生：先算6减去3等于3，再算3加上4得7。

師：加减混合运算是怎么算的？

生：从左往右依次计算。

（学生报出第（2）组的得数后，同样总结出乘除混合运算也是从左往右依次计算。）

2.出示第三组口算题

（3）3×4+6 6+3×4

生：3×4+6是先算乘法，最后得数是18；6+3×4，先算加法，再算乘法，最后得数是36。

师：你是怎么想的？

生：从左往右依次计算。

师：有道理，前面几道我们都是这么做的。有不同意见的同学吗？

生：6+3×4，应该先算乘法，等于12，再算加法，12加上6等于18。

师：（指着黑板）前面两组题目同学们都没有异议，最后一组的分歧比较大，有认为先算加法，有认为先算乘法。两种都对的可能性有吗？

生：（齐）不可能都对！

师：那到底哪种方法是对的呢？今天我们就来研究这样的算式。

【评析】有意识创设观念冲突，引发学生的真思考。乘加混合运算，有的学生认为先算加法，有的认为先算乘法。那到底是怎么算呢？一石激起千层浪。在问题和矛盾中激起了学生的探究欲望，而且思考的问题来自于学生的需要，不是老师的给予，学生探究兴趣更加的浓厚。

（二）运用情境，理解算理

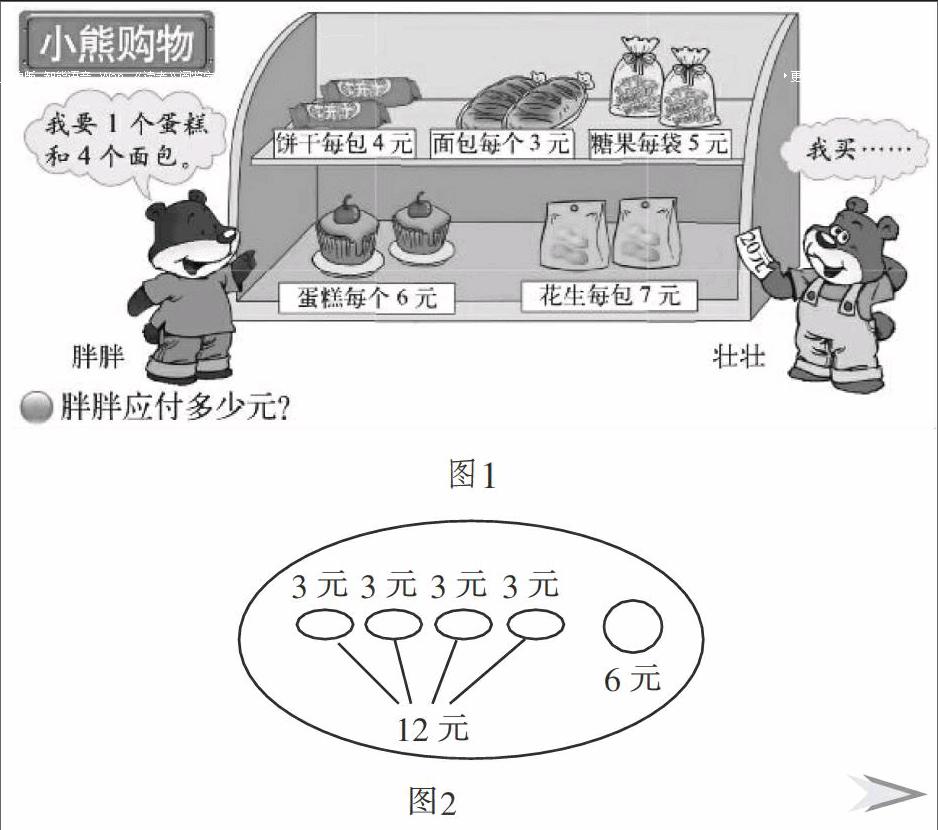
1.课件出示，看图列式（如图1）

师：从图中你了解到哪些数学信息？

生：里超市的食品有饼干、面包、糖果、蛋糕、花生……

生：我还知道了这些食品的价格。

（学生相互说一说，再指名说一说。）

提出问题：小熊胖胖买4个面包和1个蛋糕，应付多少元？

【评析】学生在丰富有趣的生活情境中，就会产生学习的愿望，从而提高学习的兴趣，更加主动地进行探索知识。购物的体验每位学生都有经历过，通过创设小熊购物的情境，联系学生的实际，激发学生的学习兴趣，为学习新课做好准备。

2.自主探究，直观理解运算顺序

师：要求胖胖应付多少元，你有哪些方法呢？在练习本上画一画，写一写吧。

（学生独立思考，教师巡视指导。）

师：你们有答案了吗？说一说你们是用什么方法解决的。

（指名学生回答，将学生的作业本投影展示。）

生1：我是用画图的方法来解决这个问题的方法的。（如图2）

师：你能说说图中每一部分表示的意思吗？

生1：一个圆圈表示一个面包，胖胖买了4个面包，每个面包3元，需要12元，右边的圆表示一个蛋糕，需要6元，一共要付18元。

师：你说的条理很清楚，其他同学有要补充的吗？

生2：我是用画图和算式结合的方法的。（如图3）

3×4=12（元） 12+6=18（元）

师：怎么说？

生2：我用一个圆圈表示一个面包，胖胖买了4个面包，每个面包3元，算式是3×4=12（元），需要12元，右边的长方形表示一个蛋糕，需要6元，算式是12+6=18（元），所以胖胖一共要付18元。

师：哦，我明白了，你是画图和算式相结合，这样可以让算式来表示我们的思考。

师：大家想一想，这两位同学画的图里都是先算出什么物品的钱？endprint

生：先算出4个面包要付的钱。

【评析】反思问题是生长新思想、新方法、新知识的种子。画图的方法能帮助学生更好地理解题目的意思，同时有利于学生分析数量关系，让学生说一说画图当中都是先算出什么物品的价钱，也为更好地理解运算顺序打好基础。

3.观察比较，建构运算顺序

师：刚才你们在思考的时候，老师发现了我们班有几位同学的方法和他们是不一样的，大家来看看吧！（展示学生的作品）

①3×4=12（元），12+6=18（元）；

②3×4=12（元），6+12=18（元）；

③3+3+3+3+6=18（元）；

④3×4+6=18（元）；

⑤6+3×4=18（元）；

师：这些算式，有什么不同的地方？

生：算式①②都是分步计算的。

生：算式④比算式③更简便。

生：算式④⑤是把算式①②合起来写的。

师：这些算式有什么共同点？

生：都要先算4个面包的钱，即先算3×4。

教师板书：3×4+6和6+3×4。

追问：这两个算式有什么相同点和不同点？

生：这两个算式的相同点是都有乘法和加法，不同点是第一个算式的乘法在前面，加法在后面；第二个算式是加法在前面，乘法在后面。

生：我有补充，这两个算式的相同点是都有3×4，不同点是第一个算式的6在后面，第二个算式的6在前面。

继续追问：在这里，3×4表示什么？

生：表示4个面包的价钱。

师：那么一个算式6在后面，另一个算式的6在前面，表示的意思一样吗？

生：第一个算式是先求面包的价钱，再求面包的价钱加蛋糕的价钱；第二个算式也是先求面包的价钱，再求蛋糕加面包的价钱，他们的意思是一样的。

生：一个是面包的价钱加蛋糕的价钱，一个是蛋糕的价钱加面包的价钱，意思是一样的。

教师小结：这两个算式都是把分步列出的两个算式整合成一个既有加法又有乘法的算式，这两个综合算式表示的实际意义是相同的，只是出现加号与乘号的先后顺序不同。

师：这两道题目刚才计算的时候我们是有歧义的。问题主要聚焦在6+3×4，是等于36还是18。通过刚才的学习，你有什么新的认识呢？

生：得数应该等于18。

师：为什么？

生：6+3×4，要先算3×4=12，就是先求出4个面包的钱，再加上1个蛋糕的钱，也就是再算6+12，所以结果是18。

生：如果先算6+3=9，再算9×4=36，等于36元。这就不是1个蛋糕和4个面包的钱了。

追问：如果先算6+3=9，你知道这是买什么物品的钱吗？

生：如果先算6+3=9，再算9×4=36，算的是4个6+3的和，表示4个面包和4个蛋糕的钱了。

师：同学们的发言很精彩，计算3×4+6和6+3×4的运算顺序是怎么样的？

生：先算乘法，再算加法。

【评析】请算法不同的学生说一说各自算式的意义。对每一种算式进行交流讨论，体会3×4+6是把“3×4=12”和“12+6=18”这两个算式合在一起，來计算一共的钱数。当然，把两个算式合并成一个综合算式也不难，而且许多学生也能直接列出综合算式。在学生列出不同算式列后，教师要从真实的生活经验出发，组织每个小组讨论各个算式的异同点，讨论算式的意义是否一样。只有这样，才能使学生在对比中理解分步算式和综合算式的关系，并在对比中学会将两个算式合成一个综合算式。同时感悟乘加混合运算“先算乘法，再算加法”的合理性。

4.说一说，再列式算一算（如图4）

学生根据图意，列出算式3+4×5、4×5+3和1+6×3、6×3+1，根据题意并分别计算。

师：（指着黑板）仔细观察这些算式，你能发现什么？

生：这些都是含有乘法和加法的综合算式。

生：计算的时候，都是先算乘法，再算加法。

小结：乘加混合运算，先算乘法，再算加法。（板书）

【评析】抽象概括是抽取“一类事物”的共同属性的过程，抽象概括的材料一定要丰富，要避免从一道算式得出一条计算法则。在教学中，教师通过“一共有多少瓶”和“一共有多少个猫警察”等多道习题的探索，再从中抽象概括出“先算乘法，再算加法”的计算法则。

5.递等式计算

师：今天学习的乘加混合运算，还可以用递等式计算。可以让大家把计算过程看得清清楚楚、明明白白。

教师板书递等式计算过程：

6+3×4

=6+12

=18（元）

重点讲清：（1）先算什么，再算什么。（2）先算的3×4等于12，怎么写到后面去了。

森林医生：下面的计算对吗？把不对的改正过来。

4+5×3 7×4+6

=9×3 =28+6

=27 =34

【评析】在教学递等式计算时，教师要把数学规定的源头所体现出的人类思维的过程呈现给学生，不仅利于学生理解，而且可以改变数学之于学生的感受——数学理性，但也有趣！

（三）课堂总结，设疑延伸

师：同学们，这堂课有什么收获吗？

追问：算式中有乘法和减法，有除法和加法，又该怎么算呢？你能用生活中的例子来解释吗？

屏幕出示：20-3×4 15+10÷5

师：请同学们课后思考思考，下节课继续学习。

【评析】后续的学习和本堂课的内容紧密联系起来，形成知识的正迁移。将反思的活动延伸到课外，使学生养成关注身边的数学问题并尝试解决的习惯，从而提高学生解决数学问题的能力。

三、教后反思

1.算用结合，体会数学的“约定”来源于生活

注重数学与生活的联系，从熟悉的生活中引入数学问题，再应用到生活中，始终重视“算用结合——解决问题”这一理念的体现，不管是情境引入部分让学生根据情境提出数学问题，或者根据算式用生活原型解释其意义，以及根据直观图表示乘加运算的意义，还是最后“你能用生活中的例子，说说每个算式的意思”，都是让学生把数学与自己的生活经验相联系，用生活中的例子解释数学学习的合理性，让学生经历数学知识生活化，生活世界数学化的过程。促进学生增强从熟悉的情境中发现数学问题，并能调动已有的知识和生活经验去理解新的数学知识，再运用数学知识解决新的问题的能力。

2.以用激算，体会数学“约定”的合理性

算式“3×4+6”和“6+3×4”的生活原型是“小熊胖胖买1个蛋糕和4个面包，共要多少元？”这个生活原型与学生的生活经验非常贴近，“共要多少钱？”这样的问题，学生在日常生活中都有遇到，也解决过类似的问题，因此学生对计算的结果是不会有怀疑的。可以说，利用生活原型来解决像“3×4+6”和“6+3×4”这样的乘加混合运算，刚好处在了学生的“最近发展区”，“跳一跳，便摘到了果子”，为学生理解“先算乘法，再算加法”提供了支撑，使学生顿悟到数学的规定与生活实际的需要有联系，不是凭空乱造的。

3.学以致用，体会计算和问题解决的“和谐”统一

现行教材已不再专门设置“应用题”领域，教材大多以“算”与“用”结合的“解决问题”的类型模块呈现，以增进学生的问题意识和应用意识。在计算教学中，让学生从现实生活中抽象出数和简单的数量关系，在具体的情境中理解算理，并应用所学的知识解决问题。重视计算和问题解决的有机整合，在计算教学中提供具体的生活情境，使计算有理有据，同时感受计算的价值和现实意义。计算教学让学生在生活情境的支撑下去理解算理，并运用所学知识去解决实际问题，往往能起到事半功倍的效果。endprint