Quantum Spin Transport in Rashba Spin-Orbit-Coupled Graphene Nanoflakes∗

H.Nikoofard,M.Laghaei,and E.Heidari Semiromi

Department of Physics,University of Kashan,Kashan,Iran

1 Introduction

Study and manufacturing of electronic nanodevices are the main interests of engineers and researchers in fundamental sciences.This is because these systems are fast and have low power dissipation for storage and transport of information.The appearance of the spintronics as a new branch of electronics has opened a wide horizon in this technology,which is the development of spin-based nanodevices to enhance storage capacity and enable encoding and fast processing of the information.[1]Quantum transport,which is the investigation of polarization of the spin of the electrons,has a substantial role in the spintronics and has been studied widely in mesoscopic systems.As an example,the quantum transport has effects in significant phenomena such as quantum Hall effect and it would allow for spin currents to be generated without dissipation.[2]

The spin polarization in a mesoscopic system is generally achieved by an external magnetic field or by connecting the system to a ferromagnetic material.However,in recent years,the generation and manipulation of the spin currents by full electrical means such as spin-orbit coupling(SOC)have become subjects of interest.If the mirror symmetry is broken,either by a perpendicular electric field via a gate voltage or by interaction with a substrate,a Rashba SOC(RSOC)is revealed.[3]The RSOC as an external electric field causes switching and control on the orientation of the spin of electron.When the electric current flows in a sheet,the spin of the electrons become polarized as a result of the cooperation of the current and the Rashba field that is assured with the presence of the substrate.[4]The tuning of the RSOC strength via the external gates[3,5]is simpler than with a magnetic field,so the two-dimensional electron systems with RSOC have become the most promising devices for spintronic applications.

Many studies have been performed on the SOC in nanostructures as a possible electrical way,which allow generation and manipulation of the spin current.For example,it is observed experimentally that a spin-polarized current is generated in a semiconductor wire due to a lateral SOC induced by an in-plane electric field.[6]Moreover,the SOC applied on a segment of the quantum wire in the presence of a constriction[7]generates a spin polarization and enhances the spin- filtering up to%95.Other studies show that the SOC can lead to the spin Hall effect in semiconductor systems.[8−11]

Understanding of the novel features of the graphene such as weak intrinsic SOC and hyper fine couplings[12]has been of interest in recent years. In particular,graphene-based transistors[13]and field-effect transistors(FET)[14]can cause an evolution in the nanoelectronics.The carbon-based devices have a controllable band structure,so it is important to investigate the quantum transport properties of these systems.[15]For example,the spin transport has been measured in suspended highmobility graphene devices that are connected to ferromagnetic leads.[16]

Several experimental reports have shown that RSOC in graphene can be larger than 200 meV[17]and the quantum spin Hall effect can occur in graphene.[18]Such observations have motivated the scientists to study the effect of the SOC in the graphene-based systems.The effect of SOC on the electronic structure of the graphene opens a small gap in the band energy.This allows the grapheneto convert from a two-dimensional semiconductor to an insulator with a quantized spin Hall conductance.[18−19]

The spin conductivity as a striking feature of the graphene can be analyzed based on the Kubo and Landauer formulas.[5]The spin-dependent transport of the graphene nanoribbons have been studied in the presence of an electric- field-induced Rashba coupling in the finite region of the system by consideration of some symmetries.[20]Also,the effect of symmetry and defect on transport properties in zigzag graphene nanoribbons are investigated.[21]A perfect spin- filtering effect and a rectifying behavior are observed for edge hydrogenated graphene nanoribbon heterojunctions.[22]The spin polarization and conductance have been calculated in a Y-shape graphene nanoribbon with three terminals in the presence of the RSOC.[23]In the case of a T-shaped conductor,the effects of the RSOC on the spin-dependent transmission probabilities and the spin filtration have been obtained.[24−26]A large spin- filtering is observed in graphene nanoribbons with zigzag edges in the presence of RSOC.[26]A similar work has performed very recently that the spin polarization has been studied using a gate voltage through a Rashba barrier in the graphene.It found that the sign of the spin polarization can switch from positive to negative by adjusting the electric potential at any RSOC.[27]There also exist technological applications of the grephene in spintronic devices.The graphene nanostrips can be used as digital memory devices in which the spin-polarized states can be treated as switchable quantum bits through the applied voltage.[28]

In this paper,we consider graphene nanodisks with various sizes as channels deposited on a substrate for inducing the RSOC.The channel is connected to semiin finite nanoribbons with armchair edges as the leads.The RSOC is provided by an underneath gate voltage applied to the central region of the device.In our approach,we start with a single-particle Green’s function in the tight binding model to calculate the transmission probability and the spin polarization of the electrons.Moreover,the spin polarization of the device in three directions is obtained by tuning the RSOC strength.We also study the effect of the size of the channel on the spin polarization.

2 Model and Method

We consider a graphene nanoflake as a channel in which the number of the plaquettes on each side,denoted byM,introduces the size of the system.The RSOC is applied to the center of the channel,as shown with the red color in the inset of Fig.1.The system is attached to two semi-in finite graphene nanoribbon leads,denoted by leadLand leadR.The total Hamiltonian of the system is

where,H0describes the kinetic energy of the itinerant electrons in the nanoflake andHRis the Rashba Hamiltonian.In Eq.(1),H0can be expressed in a tight-binding model in terms of the electronic hopping between the nearest neighbor atomic sites;

where〈n,m〉denotes the summation over the nearest neighbor sites,t=2.66 eV is the nearest-neighbor hopping integral,andc†n,σ(cn,σ)is the creation(annihilation)field operator of an electron at then-th site with the spinσ(↑,↓).In Eq.(1),His given by[26]R

wheredn,mis a displacement vector between the two nearest-neighbor atoms fromm-th ton-th site,αrepresents the Rashba SOC strength,andais the carboncarbon bond length. The advanced(retarded)singleparticle Green’s function can be written as follows[29]

whereHCis the Hamiltonian of the channel.The self energy of the leadα(=L,R)is

wheregαis the surface Green’s function at the interface of the channel and the leadα.HαCis the coupling between the leadαand the channel.We calculateGLσσR′by the Keldysh formalism as the spin-resolved conductance of the electrons with the injected Fermi energyEand the spinσfrom the left lead(L)and detected with the spinσ′from the right lead(R),[20]

Here,Γ is the coupling matrix for the leadαthat is related to self-energies as follows

The transmission probability of the electron,Tσσ′,will be generalized to a 2×2 matrix in the spin space with spin-conserving components(diagonal)and spin- flipping components(off-diagonal)[23]

If the incident current is unpolarized,then the spin polarization of the current detected in the right lead inx,y,andzdirection is calculated by using the Eq.(8)

and the total spin polarization is defined by

3 Results and Discussion

In this section,the transmission probability and the spin polarization are calculated versus the Fermi energy for various strengths of RSOC and several sizes of the system.The direction of the electric field which determines the strength of RSOC is chosen along thezaxis.This is also used as the direction of the spin quantization.According to the experimental data for the strengths of RSOC in the graphene-based nanomaterials,[17]we consider the range(0–0.2)eV forαin the following.

Fig.1 (Color online)Spin-up and spin-down transmission probabilities as a function of the Fermi energy of the injected electrons for M=10 and two values of α=0 and 0.2 eV.Inset:Schematic representation of the channel for M=10.

Figure 1 shows the variation of the spin-up and spindown transmission probabilities as functions of the Fermi energy of the injected electrons for two values of the Rashba strength(α=0 and 0.2 eV).The considered channel forM=10 is sketched in the inset.The electrons are injected from the left side of the channel and detected at the right side.The dotted curves are for the situation that the edges of graphene nanoribbon are terminated with hydrogen atoms.In Fig.1,the transmission probabilities are nearly zero aroundE/t=0,but the probabilities grow with the enhancement of the energy.The steps in the curves are irregular because of the backscattering of the electrons that occurs in the channel.This is due to the bending in the region of the channel that RSOC is applied from a straight nanoribbon.In the absence of the RSOC(α=0),the transmission probabilities are even functions with respect to the Fermi energy due to the time reversal symmetry in the system.However,this symmetry breaks down with turning on the Rashba field.By increasing the Rashba strength,the transmission probabilities remain unchanged at small values of the energy(E/t≾0.1).Then,the probabilities decrease for the higher energies(E/t≿0.1).This is because the RSOC rotates the spin of the electrons and then,the transmission probabilities of the electrons with the initial spin direction decrease.This achievement is in agreement with the result of Ref.[27]in which the transmission probability is larger for lower gate voltages.The mentioned change in the spin orientation by the RSOC is useful in the applications that use a gate voltage for the spin filtration.

If we consider the graphene nanorribbon with hydrogen-terminated edges,the length of the C-C bond in the edge shortens.So,this kind of geometric deformation causes increasing of the hopping parameter between two neighboring carbon atoms on the graphene nanoribbon edge.[30]By attention to dotted curves in Fig.1 we see that the transmission probability decreases slightly for the most of the values of the Fermi-energy.This decrease is a result of backscattering of the electrons waves from hydrogen atoms that act as defects on the edges.Besides,the energy interval that the transmission probability is zero decreases.Also the fluctuations of the transmission probability become more in the presence of the hydrogenterminated edges.This is due to the quantum interference of the electrons waves.By comparison of Figs.1(a)and 1(b),one observes that the behavior of the spin-up and spin-down transmission probabilities are similar to each other.This indicates the presence of a kind of symmetry in the system with respect to the orientation of the spin of the electrons. Also for an arbitrary energy in the presence of RSOC(α=0.2 eV),one observes thatT↑↑(E)=T↓↓(−E).

Fig.2 (Color online)Spin-up and spin-down transmission probabilities as a function of the Rashba strength for M=10 and two values of the Fermi energy.The solid and dotted lines show T↑↑ for E/t=0.29 and E/t=−0.29,respectively.The dashed line represents T↓↓ for E/t= −0.29.The solid and dashed lines fall on each other.Inset:Schematic representation of the channel for M=10.

Figure 2 shows the variation of the transmission probabilities with the Rashba strength for two values of the Fermi energyE/t=0.29 and−0.29 in the channel withM=10.In the absence of the RSOC(α=0),we haveT↑↑(E)=T↑↑(−E)=T↓↓(−E).By switching on the Rashba field and increasingα,an overall decreasing occurs and the above relation changes toT↑↑(E)=T↓↓(−E)/=T↑↑(−E).These results are in agreement with Fig.1.

The effects of the RSOC on the components of the spin polarization are shown in Fig.3.In this figure,Px,PyandPzare plotted with respect to the Fermi energy for several values ofα.In Figs.3(a)–3(c),an antisymmetry exists with respect toEfor all values ofα.Also,in these figures,there is a region around the zero Fermi energy where the spin polarizations become zero,which is due to the gap in the energy levels.[20]However,outside this interval,a sudden increase is seen in the spin polarizations for specific energies.The sudden increase in the spin polarizations allows one to choose energies corresponding to strong spin filtrations.In Figs.3(a)–3(c),the components of the spin polarization oscillate by the enhancement of the energy,and the heights of the peaks suppress and decay to the zero.The origin of these oscillations is multiple reflections of the spin waves and their resonance in the channel.By increasingα,more oscillations are observed inPx,PyandPz.All components of the spin polarization have zero value in the absence of the Rashba field,but they increase with enhancement the Rashba strength.Also,in Figs.3(a)and 3(c)a change in the sign is observed in the plots ofPxandPzwith increasing the energy at all Rashba strengths.These results indicate that the sign and the magnitude of the spin polarizationPxandPzcan be controlled by tuning the gate voltage.Also,the spin polarization in thez-direction(Pz),which is obtained through the difference between the transmission probabilities according to Eq.(9),becomes lower when the energy increases.It has the maximum value atE/t=0.215,which is in agreement with Fig.1.

In Fig.3(d),three components of the spin polarization are compared with each other for the value ofα=0.2 eV.The value of the maximum ofPyis larger than those of the other components in 0.1＜E/t＜0.5.This shows that the channel has a good filtration behavior for theycomponent of the spin polarization in this range of the energy.Also in this figure,Pxis zero inE/t∼0.287 andPzis zero inE/t∼0.3,which indicate that one can have a control on the spin filtration by variation of the Fermi energy.In Fig.4,the total spin polarization is plotted with respect to the Fermi energy for several Rashba strengths.The total spin polarization is an even function of the Fermi energy.

The spin-up transmission probability and the total spin polarization are shown in Fig.5 for several sizes of the system and forα=0.2 eV.In Fig.5(a),the transmission probability is an increasing function with enhancement of the size of the system at a fixed Fermi energy.Besides,the energy interval that the transmission probability is zero decreases with the size of the system.This is because for the larger sizes of the system,the number of accessible energy levels for the injected electrons is higher.The similar effects are observed for total spin polarization in the range 0.1＜E/t＜0.5 in Fig.5(b).Also,the fluctuations of the spin polarization increase with the size of the system.

Fig.3 (Color online)Components of the spin polarization as a function of the Fermi energy for M=10 and various values of the Rashba strength in Figs.3(a)–3(c).These components are shown particularly for α =0.2 eV in panel(d).Schematics of the channel for M=10 is shown in the right bottom of the figure.

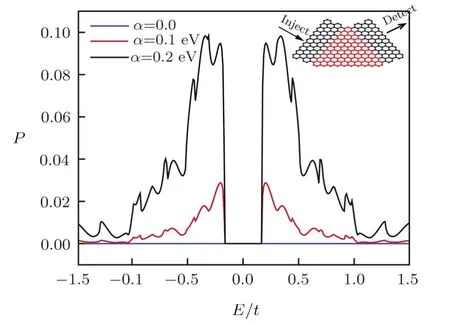
Fig.4 (Color online)Total spin polarization versus the Fermi energy for M=10 and various values of the Rashba strength.Inset:Schematic representation of the channel for M=10.

Fig.5 (Color online)Spin-up transmission probability and total spin polarization with respect to the Fermi energy for several sizes of the system at α=0.2 eV.

Figure 6 shows the effect of the size of the channel on the components of the spin polarization with respect to the Fermi energy forα=0.2 eV.In all panels of this figure,the fluctuations of the spin polarization become more with size of the system.The heights of the largest peaks in the plots grow with increasing the size of the system.So,the ability to perform spin filtration enhances with the size of the channel.In Fig.6,as the size increases,the maximum amplitudes of the plots occur in lower energies.This is because the number of available energy levels for the electrons increases with the size of the system as mentioned before.In the range 0＜E/t＜0.5,one can have a control on the type of the spin filtration,by variation of the Fermi energy.For example,Pxhas a zero value forM=10 atE/t=0.284,butPyandPzare nonzero in these parameters of the system.Moreover,the spin filtration can be controlled by changing the size of the system,e.g.all of the components of the spin polarization are nonzero forM=13 atE/t=0.284,butPxhas a zero value forM=4 and 10 at this energy.

Fig.6(Color online)Three components of the spin polarization with respect to the Fermi energy for several sizes of the system at α=0.2 eV.

Fig.7 Transmission probability in the absence(solid curves)and presence of defect(dashed curves)as a function of the Fermi energy of the injected electrons for M=10 and α=0.2 eV.Inset:Schematic representation of the channel with defect for M=10.

We have introduced a single defect as vacancy into this system and the result is plotted in Fig.7.In this figure,the transmission probability is shown for spin-up and spindown(in the presence and in the absence of defect)forM=10 andα=0.2 eV.The transmission probabilities are reduced although the overall behavior remains almost unchanged in comparison with the system without defect.This reduction is due to the effect of the backscattering of the electrons waves from the defect in this system Also,the difference between the spin-up and the spin-down transmission coefficients increases with introducing the defect to system.

4 Conclusion

In this paper,the transmission probabilities and the spin polarization are investigated in the presence of RSOC via a gate voltage in the graphene nanoflake systems.The variation of the transmission probability is studied with respect to the Fermi energy of the electrons.This shows that out of the region of the zero energy,the transmission probability is growing by enhancement of the energy.Besides,the spin polarization increases with the enhancement of the Rashba strength and oscillates by variation of the energy.Also,the amplitudes of the peaks of the spin polarization decay to zero for all values of the Rashba strength.This indicates that the sign and the magnitude of the spin polarization can be controlled by tuning the gate voltage.Moreover,the effects of the size of the system on the transmission probability and the spin polarization is investigated.This shows that there is a control and manipulation of the spin filtration by means of the variation of the Rashba strength and the size of the system.The obtained results are applicable for electrical control on the spin transport in graphene-based nanodevices.

[1]I.Zutic,J.Fabian,and S.D.Sarma,Rev.Mod.Phys.76(2004)323.

[2]S.Murakami,N.Nagaosa,and S.C.Zhang,Phys.Rev.Lett.93(2004)156804.

[3]Y.A.Bychkov and E.I.Rashba,J.Phys.C 17(1984)6039.

[4]A.Dyrdal and J.Barnas,Phys.Rev.B 92(2015)165404.

[5]M.I.Katsnelson,Eur.J.Phys.B 51(2006)157.

[6]P.Debray,et al.,Nat.Nanotechnol.4(2009)759.

[7]J.F.Liu,Z.C.Zhong,L.Chen,D.Li,C.Zhang,and Z.Ma,Phys.Rev.B 76(2007)195304.

[8]S.Murakami,N.Nagaosa,and S.C.Zhang,Science 301(2003)1348.

[9]J.Sinova,et al.,Phys.Rev.Lett.92(2004)126603.

[10]Y.K.Kato,et al.,Science 306(2004)1910.

[11]J.Wunderlich,B.Kaestner,J.Sinova,and T.Jungwirth,Phys.Rev.Lett.94(2005)047204.

[12]D.Huertas-Hernando,F.Guinea,and A.Brataas,Phys.Rev.B 74(2006)155426.

[13]J.B.Oostinga,H.B.Heersche,X.Liu,A.F.Morpurgo,and L.M.K.Vandersypen,Nat.Mater.7(2007)151.

[14]F.Schwierz,Nat.Nanotechnol.5(2010)487.

[15]Z.Wang,N.Hao,and P.Zhang,Phys.Rev.B 80(2009)115420.

[16]M.H.D.Guimaraes,et al.,Nano Lett.12(2012)3512.

[17]Y.S.Dedkov,M.Fonin,U.Rudiger,and C.Laubschat,Phys.Rev.Lett.100(2008)107602.

[18]C.L.Kane and E.J.Mele,Phys.Rev.Lett.95(2005)226801.

[19]N.A.Sinitsyn,J.E.Hill,H.Min,J.Sinova,and A.H.Mac-Donald,Phys.Rev.Lett.97(2006)106804.

[20]L.Chico,A.Latge,and L.Brey,Phys.Chem.Chem.Phys.17(2015)16469.

[21]Y.Ren and K.Q.Chen,J.Appl.Phys.107(2010)044514.[22]J.Zeng,K.Q Chen,J.He,X.J.Zhang,and C.Q.Sun,J.Phys.Chem.C 115(2011)25072.

[23]J.F.Liu and K.S.Chan,J.Phys.Soc.Jpn.82(2013)074711.

[24]M.Yamamoto,T.Ohtsuki,and B.Krame,Phys.Rev.B 72(2005)115321.

[25]A.A.Kiselev and K.W.Kim,Appl.Phys.Lett.78(2001)775.

[26]J.F.Liu,K.S.Chan,and J.Wang,Nanotechnology 23(2012)095201.

[27]X.Wu,J.Phys.D:Appl.Phys.49(2016)105305.

[28]D.Gunlycke,D.A.Areshkin,J.Li,J.W.Mintmire,and C.T.White,Nano Lett.7(2007)3608.

[29]S.Datta,Electronic Transport in Mesoscopic Systems,Cambridge University Press,Cambridge(2002).

[30]Z.F.Wang,Q.Li,H.Zheng,H.Ren,H.Su,Q.W.Shi,and J.Chen,Phys.Rev.B 75(2007)113406.