Electrostatic Surface Waves on Semi-Bounded Quantum Electron-Hole Semiconductor Plasmas

Afshin Moradi

Department of Engineering Physics,Kermanshah University of Technology,Kermanshah,Iran

1 Introduction

The propagation of plasma waves in quantum electronhole semiconductor(QEHS)plasmas have been of considerable interest in recent years. Misra[1]studied the propagation of surface electromagnetic waves in a magnetized QEHS plasma,using quantum hydrodynamic(QHD)model.He found a forward propagating mode by including the quantum tunneling effect.Moslemet al.[2]investigated the propagation of nonlinear acoustic waves in a QEHS plasma,by means of QHD theory.They studied the contributions of the tunneling of degenerate plasma species through the Bohm potential barrier,the exchange interactions and correlations,and the statistical quantum pressures of degenerate electron and hole fluids on the acoustic pulse profile.Then,by employing QHD model,Zebaet al.[3]investigated the electron-hole two-stream instability in a QEHS plasma.

Furthermore,Yahiaet al.[4]studied the behavior and instability of the electrostatic perturbations in a QEHS plasma pumped by energetic electron beam,taking into account the exchange-correlation effects,the quantum statistical pressures,and the quantum recoil effects of the degenerate electrons and holes,as well as the electron beam parameters.Then the investigation of the quantum effects in the properties of linear and nonlinear quantum electrostatic acoustic waves in a QEHS plasma has been followed by Wang and Eliasson,[5]using the QHD theory.In this way,Wang and Lu[6]described the modulational instability of the quantum acoustic waves in a QEHS plasma taking into account the combined effects of the quantum recoil,the exchange-correlation potential standing for spin,the degenerate pressure effects,as well as the electronphonon(hole-phonon)collision.Also,Amin[7]reported the nonlinear dispersions of the wave propagating in the QEHS plasmas.

However,despite this wealth of theoretical information about the optical properties of the unbounded QEHS plasmas,there is no available theoretical account of surface waves propagation on the semi-bounded QEHS plasmas with nonlocal character,while in reality,under laboratory conditions or in micro-and nanoelectronic devices,plasmas are spatially limited.Therefore,it is important to study the boundary effect on the nature of the QEHS plasmas.

On the other hand,in our previous investigations,the propagation of electrostatic surface waves on a semibounded quantum metallic plasma(one-species plasma system)in the absence[8]and presence of an external magnetic field[9]was studied,by using the one- fluid QHD model.For semiconductor plasmas(two-species plasma system),we may treat the electron and hole components as two distinct but interacting fluids.[10−11]In this way,we may expect to find two types of oscillations.One of them is the usual plasma oscillation.[8]The other is an oscillation associated with a density wave similar to a sound wave in gases.In light scattering experiments,Pinczuket al.[12]have observed the acoustic mode in bulk GaAs samples.

In the present work,motivated by the previous papers,[1−7]and our new findings for the properties of the surface and bulk waves on the electron-hole semiconductor nano-spheres[10]and nano-wires,[11]we wish to study the electrostatic surface waves on the semi-bounded QEHS plasmas.In this way,by using the linearized QHD theory,Poisson equation and applying the appropriate boundary conditions,we obtain a general analytical expression forthe dispersion relation of surface waves on semi-bounded QEHS plasmas.We note that for semiconductor quantum devices working with the electrons and holes in nanoscale sizes,it is important to study the quantum effects on the dynamics of the charged carriers.The quantum effects(e.g.,quantum recoil effects,degenerate pressures of the plasma species,as well as the exchange and correlations)are expected to play an important role in the collective behavior of the QEHS plasma.[2]

2 Formulation of Problem

We consider a homogeneous unmagnetized two component QEHS plasma occupying the half-spacez＞0 and bounded by vacuum,i.e.,z＜0 in a Cartesian coordinate system withR=(r,z)wherer=(x,y).The electrostatic surface waves are supposed to propagate parallel to the interfacez=0 along thex-andy-direction.Thus,the QEHS plasma with the densityn0i(per unit volume),wherei=e(for electrons)andi=h(for holes)will be perturbed by the surface waves and may be regarded as two charged fluid with three-dimensional scalar density fieldni(R,t)and vector velocity fieldui(R,t).The nonlinear dynamics of such disturbances are governed by the following set of QHD equations:[2]

whereϵis the relative dielectric constant of the system,eis the element charge,m∗iis the effective mass,q=−1 for electrons andq=+1 for holes and Φ is the self-consistent electrostatic potential.The second term in the right-hand side of Eq.(2)is due to the non-relativistic degenerate particle pressurePiand is given by[13]

where ħ is the Planck constant divided by 2π.The third term in Eq.(2)represents the electron and hole exchange correlation force between the identical particles when their wave functions overlap due to the high number density.The exchange-correlation potentialVxcifor the electrons and holes are given by:[14−16]

Here,we consider only the first order perturbations by lettingni=n0i+n1iwithn0i≫n1i;ui=u1i;and Φ = Φ1,wheren1i,u1i,and Φ1are the perturbed quantities.As a result,we obtain the following linearized equations:

where

By eliminating the velocity fieldu1ifrom Eqs.(4)and(5),and using Eq.(6),one can obtain the following equations

and apply it to Eqs.(6)–(8),wherek=kxˆex+kyˆey.Now,we expand the perturbed densityn1i(R,t)into¯ni(k,z,ω)and electrostatic potential Φ1(R,t)into¯Φ(k,z,ω)according to Eq.(9)and considerk2≫∂2/∂z2(the very slow nonlocal variations are neglected[18]),wherek2=k2x+k2y.We find:

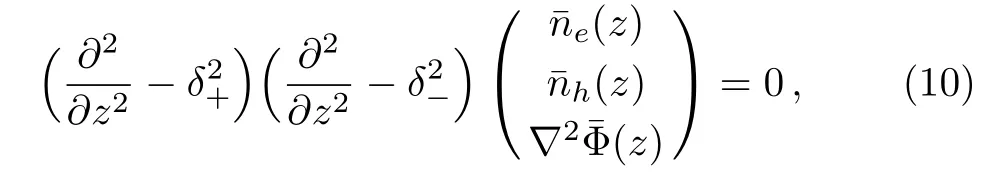
where

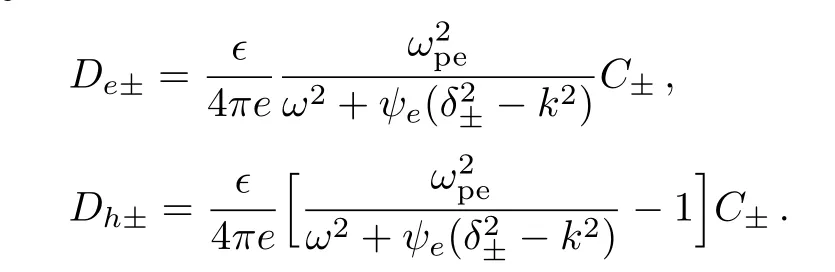
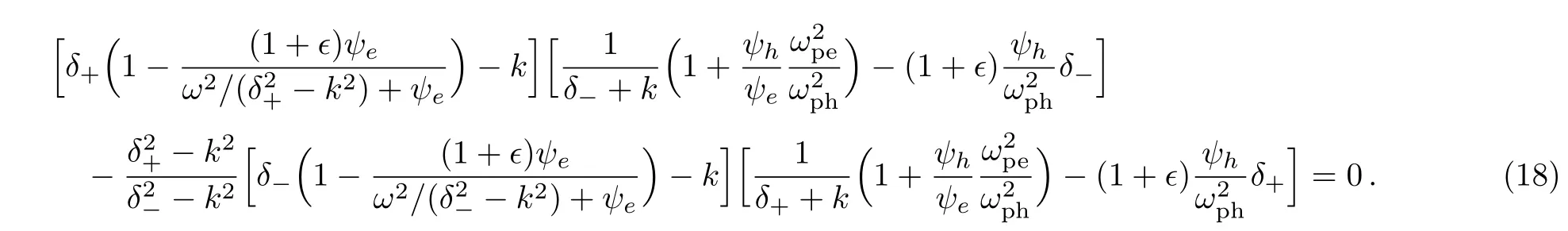
The above dispersion relation of the electron-hole wave oscillations is the original result of the present work.In the following section,we show that Eq.(18)reveals two branches of solutions for electrostatic waves viz.a low frequency and a high frequency mode.It may be mentioned that in the limitm∗h→∞andϵ=1 the low frequency branch of the above equation gets suppressed and the other branch gives the main result in Refs.[19]and[20].

3 Numerical Results and Discussion

In order to study the behavior of the propagating modes numerically,it is convenient to transform the dispersion relations Eq.(18)in a more suitable form by introducing the following dimensionless variables:Ω,K,He,N,M,η,ϑ,Ξ,Γi,Λi,Σi,Ψi,and Δ±(see appendix).Thus,in terms of these variables we can write Eq.(18)as:

To see clearly behaviour of the surface waves dispersion curves of the semi-bounded QEHS plasmas,we plot dimensionless frequency Ω,versus dimensionless variableKfrom Eq.(19),and results are depicted in Fig.1.In this way,we use the GaAs semiconductor with typical parameters[2−3]n0e=n0h= 4.7×1016cm−3,and GaSb semiconductor with typical parameters[2−3]n0e=n0h=1.6×1017cm−3,m∗e=0.047meg,m∗h=0.4meg,andϵ=15.69.Also,we considerm0=0.1meg,n0=1016cm−3,ϵ∗=10.From Fig.1,it is clear that medium supports two modes of electrostatic surface waves(i)a low frequency mode(acoustic mode)and(ii)a high frequency mode.It is easy to find that the low frequency mode shows saturation behavior for large wavenumbers and for small wavenumbers(the long wavelength limit),the acoustic mode could propagate on surface of the semi-bounded QEHS plasmas due to the mass difference between the electrons and holes.This result is similar to surface plasma oscillations in quantum electron-ion plasma half-space.[21]On the other hand,the high-frequency surface plasma oscillations are primarily due to charge separation,where the electrons and holes oscillate against each other with opposite phases.One can find that the high frequency mode has a lower cutoff and its lower cutoff frequency is

Now,we examine the effect of the electron density concentration on the dispersion relation of plasma modes,as shown in Fig.2. Here,we use the GaN semiconductor with typical parameters[2−3]m∗e= 0.13meg,m∗h=1.3meg,ϵ=11.3 and variable number densityn0e=n0h=1×1017cm−3,n0e=n0h=2×1017cm−3andn0e=n0h=4×1017cm−3.On increasing the density concentration,frequency of the surface waves increases,where curves separation is more significant for high-frequency mode.Finally,let us investigate the exchange-correlation and quantum recoil effects on the dispersion relation of surface modes. We find in the presence of the quantum recoil effect,the frequency of high-frequency surface plasma mode shifts toward high frequency(not shown here),while the dispersion relation is almost unchangeable by the exchange-correlation effects.

Fig.1 (Color online)Dispersion curves ω/ω0vs.the variable kα0/ω0for GaAs(blue line)and GaSb(red line)semibounded semiconductor plasmas.

4 Conclusion

To summarize,we have studied the electrostatic surface waves on semi-bounded QEHS plasmas.In this regards,we have used two- fluid hydrodynamic theory in conjunction with the Poisson equation and appropriate boundary conditions. We have derived the dispersion characteristics of surface electrostatic oscillations of semibounded QEHS plasmas. Numerical results show the existence of one high-frequency branch due to chargeseparation effects and one low-frequency branch due to the balance between pressure and inertia of the electrons and holes.The results may be useful for understanding the dispersion properties of quantum surface waves in semiconductor plasmas,which may be observed experimentally.

Appendix

The dimensionless variables Ω andK,are given byΩ =ω/ω0a ndK=kα0/ω0,where we haveandAlso,the dimensionless variablesΨi,and Δ±are given by

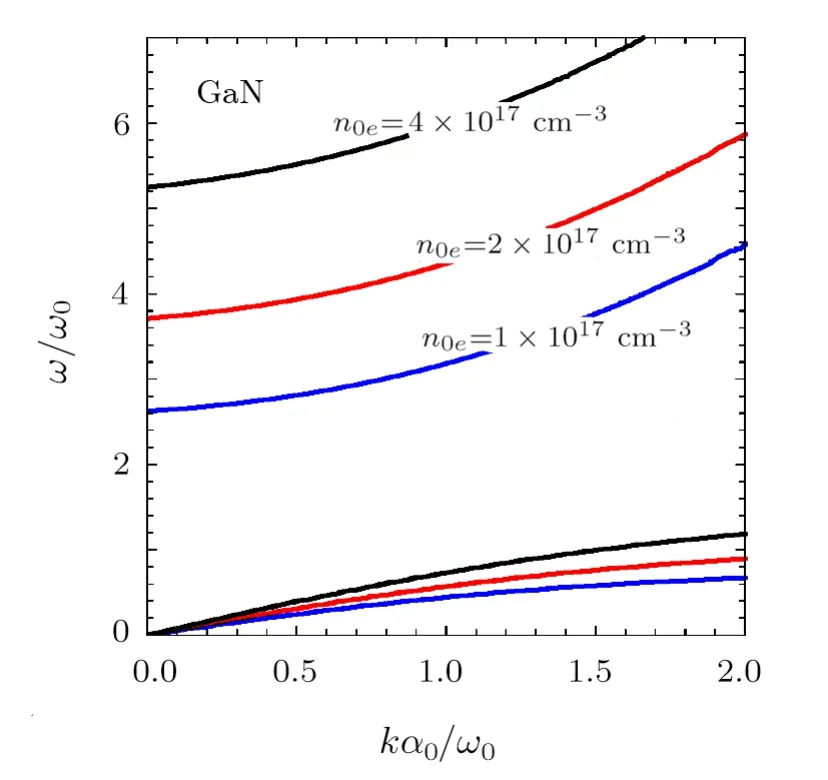
Fig.2(Color online)Dispersion curves ω/ω0vs.the variable kα0/ω0for GaN semi-bounded semiconductor plasmas with variable number density of n0e=n0h=1×1017cm−3(blue line)n0e=n0h=2×1017cm−3(red line)and n0e=n0h=4×1017cm−3(green line).

[1]A.P.Misra,Phys.Rev.B 83(2011)057401.

[2]W.M.Moslem,I.Zeba,and P.K.Shukla,Appl.Phys.Lett.101(2012)032106.

[3]I.Zeba,M.E.Yahia,P.K.Shukla,and W.M.Moslem,Phys.Lett.A 376(2012)2309.

[4]M.E.Yahia,I.M.Azzouz,and W.M.Moslem,Appl.Phys.Lett.103(2013)082105.

[5]Y.Wang and B.Eliasson,Phys.Rev.B 89(2014)205316.

[6]Y.Wang and X.Lu,Phys.Plasmas 21(2014)022107.

[7]M.R.Amin,Phys.Scr.90(2015)015601.

[8]A.Moradi,Phys.Plasmas 22(2015)014501.

[9]A.Moradi,Phys.Plasmas 23(2016)034501.

[10]A.Moradi,Phys.Scr.91(2016)105802.

[11]A.Moradi,Phys.Plasmas 23(2016)114503.

[12]A.Pinczuk,J.Shah,and P.A.Wolff,Phys.Rev.Lett.47(1981)1487.

[13]I.Villo-Perez,Z.L.Miskovic,and N.R.Arista,Plasmon Spectra of Nano-Structures:a Hydrodynamic Model,eds.A.Aldea and V.Barsan,Trends in Nanophysics,Springer,New York(2010).

[14]L.Brey,J.Dempsey,N.F.Johnson,and B.I.Halperin,Phys.Rev.B 42(1990)1240.

[15]C.X.He and J.K.Xue,Chin.Phys.B 22(2013)025202.

[16]K.Mebrouk,L.A.Gougam,and M.Tribeche,Commun.Theor.Phys.65(2016)73.

[17]P.K.Shukla and B.Eliasson,Phys.Usp.53(2010)51.

[18]M.Lazar,P.K.Shukla,and A.Smolyakov,Phys.Plasmas 14(2007)124501.

[19]M.Shahmansouri,Phys.Plasmas 22(2015)092106.

[20]H.Khalilpour,Phys.Plasmas 22(2015)122112.

[21]A.Moradi,Phys.Scr.90(2015)085601.