Self-similar Solution of a Cylindrical Shock Wave under the Action of Monochromatic Radiation in a Rotational Axisymmetric Dusty Gas

G.Nath and P.K.Sahu

Department of Mathematics,Motilal Nehru National Institute of Technology Allahabad,Allahabad–211004,

Uttar Pradesh,India

1 Introduction

The study of shock waves in the mixture of a gas and small solid particles is of great importance due to its applications to nozzle flows,lunar ash flows,bomb blasts,coal-mine blasts,underground,volcanic and cosmic explosions,metallized propellant rockets,supersonic flight in polluted air,collision of coma with a planet,description of star formation,particle acceleration in shocks,shocks in supernova explosions,the formation of dusty crystals and many other engineering problems(see Refs.[1]–[12]).An analytical solution of a planar dusty gas flow with constant velocities of the shock and the piston moving behind it was obtained by Miura and Glass.[9]Since the volume occupied by the solid particles mixed into the perfect gas is neglected by them,the dust virtually has a mass fraction but no volume fraction.Their results reflect the influence of the additional inertia of the dust upon the shock propagation.Paiet al.[1]generalized the well known solution of a strong explosion because of an instantaneous release of energy in gas(Sedov,[13]Korobeinikov[14])to the case of two-phase flow of a mixture of small solid particles and perfect gas,and brought out the key effects due to presence of dusty particles on such a strong shock wave.Paiet al.[1]have taken non-zero volume fraction of solid particles in the mixture,their results reflect the influence of both the decrease of mixture compressibility and the increase of mixture’s inertia on the shock propagation(see,Pai,[15]Steiner and Hirschler,[16]Vishwakarma and Nath[17]).

In recent years considerable attention has been given to study the interaction between gas dynamics and radiation.When the effects of radiation are taken under consideration in gas dynamics the fundamental non-linear equations are very complicated type and thus it is essential to determine approximations which are physically accurate and afford considerable simplifications.The problems of the interaction of radiation with gas dynamics have been studied by many authors by using the self-similar method developed by Sedov,[13](see Marshak,[18]Elliott,[19]Wang,[20]Helliwell,[21]Nicastro,[22]Ray and Bhowmick[23]and many others). Many researchers have investigated the motion of a gas under the action of monochromatic radiation(see,Khudyakov,[24]Zheltukhin,[25]Nath and Takhar,[26]Nath,[27]Vishwakarma and Pandey,[28]Nath and Sahu[29]).

The experimental studies and astrophysical observations show that the outer atmosphere of the planets rotates due to rotation of the planets.Macroscopic motion with supersonic speed occurs in an interplanetary atmosphere and shock waves are generated.Thus the rotation of planets or stars significantly affects the process taking place in their outer layers,therefore question connected with the explosions in rotating gas atmospheres are of definite astrophysical interest.In all of the works,mentioned above,the gas is either perfect or non-ideal under the action of monochromatic radiation.The effects of the presence of small solid particles in rotating medium are not taken into consideration by any of the authors under theaction of monochromatic radiation.In the present work,we generalize the solution of Nath[27]in perfect gas to the case of dusty gas(a mixture of perfect gas and small solid particles)by taking into account the axial component of fluid velocity and the component of the vorticity vector.Singh[30]has considered same problem with the assumption that medium to be non-rotating,whereas we have considered the medium to be rotating.

The purpose of this study is to obtain similarity solutions for the cylindrical shock wave propagating in rotational axisymmetric dusty gas with monochromatic radiation(Nath,[31−33]Levin and Skopina[34]).The components of fluid velocity in the ambient medium are assumed to vary and obey the power laws.Also,the angular velocity of rotation of the ambient medium is assumed to be obeying a power law and to be decreasing as the distance from the axis increases.It is expected that such an angular velocity may occur in the atmospheres of rotating planets and stars.In order to get some essential features of the shock propagation,small solid particles are considered as a pseudo- fluid and the mixture at a velocity and temperature equilibrium with a constant ratio of specific heats(Pai[15]).Also,the heat conduction and viscous stress of the mixture are assumed to be negligible(Refs.[1–2,16–17]).

Effects of change in the index for the time dependent energy law,the ratio of the density of solid particles to the initial density of the gas,the mass concentration of solid particles in the mixture and the radiation parameter are worked out in detail.It is observed that shock strength decreases in rotating medium.

2 Equations of Motion and Boundary Conditions

In Eulerian coordinates,the system of equations of gas dynamics describing the unsteady,adiabatic and cylindrically symmetric one-dimensional rotational axisymmetric flow of mixture of a perfect gas and small solid particles under the action of monochromatic radiation,may be expressed in the form(c.f.Paiet al.,[1]Vishwakarma and Nath,[17]Khudyakov,[24]Nath,[27]Nath,[31−33]Levin and Skopina,[34]Zedan[35])whererandtare independent space and time coordinates;u,v,andware the radial,azimuthal and axial components of the fluid velocity→qin the cylindrical coordinates(r,θ,z);p,emandρare the pressure,the internal energy per unit mass,and the density of the mixture respectively;jis the monochromatic radiation at a radial distancerand timet,Kis the absorption coefficient.

The equation of state of the mixture of a perfect gas and small solid particles can be written as(Vishwakarma and Nath,[17]Nath,[36−37]Pai,[15]Singh[30])

whereR∗is the gas constant;Tis the temperature of the gas(and of the solid particles as the equilibrium flow condition is maintained);Kp=msp/mmixis the mass fraction(concentration)andZ=Vsp/Vmis the volume fraction of the solid particles in the mixture,wheremspandVspare the total mass and the volumetric extension of the solid particles and “Vm” and “mmix” are the total volume and total mass of the mixture.

The specific volume of solid particles is assumed to remain unchanged by variations in temperature and pressure.Therefore,the equation of state of solid particles in the mixture is,simply,

whereρspis the species density of the solid particles.

The internal energy per unit mass of the mixture can be written as(see Nath,[37]Pai,[15]Paiet al.[1])

where Γ is the ratio of the specific heats of the mixture which is given by(Paiet al.,[1]Pai[15])

whereγ=cp/cv,δ′=Kp/(1−Kp),β′=Csp/Cv;CpandCvare specific heat of gas at constant pressure and constant volume;Cspis the specific heat of solid particles;CvmandCpmare specific heat of the mixture at constant volume and constant pressure.

Also,

where“A”is the angular velocity of the medium at radial distancerfrom the axis of symmetry.In this case the vorticity vector

has the components

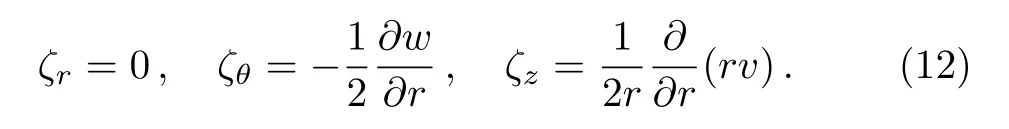
The absorption coefficientKis considered to vary as(Nath,[27]Nath and Takhar,[26]Khudyakov[24])where the coefficientK0is a dimensional constant and the exponentsα,δ,q,s,lare rational numbers.

A diverging cylindrical shock wave is supposed to be propagating outwards from the axis of symmetry into the mixture of perfect gas and small solid particles with constant density,which has zero radial velocity,variable azimuthal,and axial velocities.The flow variables immediately ahead of the shock front are

wherev∗,w∗,σ,andµare constants,Ris the shock radius,and the subscript“0” refers to the condition immediately ahead of the shock.

The momentum equation(2)in undisturbed state of mixture of perfect gas and small solid particles,gives

Ahead of the shock,the components of the vorticity vector,therefore vary as

The initial angular velocity of the medium at radial distanceRis given by,from Eq.(11),

From Eqs.(16)and(22),we find that the initial angular velocity vary as

The expression for the initial volume fraction of the solid particlesZ0is given by whereG0=ρsp/ρgais the ratio of the density of the solid particles to the initial species density of the gasρgain the mixture.

The Rankine–Hugonite conditions i.e.the jump conditions at the shock wave,which are transparent for the radiation flux,are given by the principle of conservation of mass,momentum and energy across the shock(c.f.Nath,[27]Vishwakarma and Pandey,[28]Nath,[31,33]Zel’dovich and Raizer,[38]Chaturani[39])namely,where the subscript “1” denotes the conditions immediately behind the shock front,U(=dR/dt)denotes the velocity of the shock front.From Eq.(25),the conditions across a shock front becomes

whereM∗=(ρ0U2/γp0)1/2is the shock-Mach number referred to the frozen speed of sound(γp0/ρ0)1/2.The density ratioβ(0＜β＜1)across the shock front is obtained by the relation

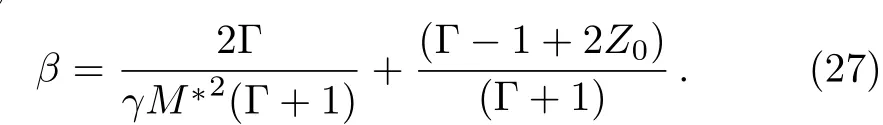
The total energy“E”of the flow field behind the shock is not constant,but assumed to be time dependent and varying as(Rogers,[41]Director and Dabora[40])

whereE0andmare constants.Here,attention is confined to positive value ofmonly,that is,to those case in which the total energy increases with time.This increase can be achieved by the pressure exerted on the fluid by the inner expanding surface(a contact surface or a piston).This surface may be,physically,the surface of the stellar corona or the condensed explosives or the diaphragm containing a very high pressure driver gas.

Following Levin and Skopina[34]and Nath,[31−32]we obtained the jump conditions for the components of vorticity vector across the shock front as

The dimension of the constant coefficientK0in Eq.(13)isgiven by (Singh,[30]Vishwakarma and Pandey[28])

For the self-similar solution(Sedov[13])the relation betweenρ0,j0,p0is given as

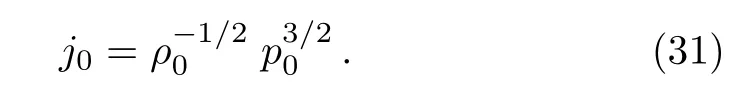
Also,for self-similarity the radiation absorption coeffi cientK0must be dependent on the dimensions ofj0,ρ0,which is equivalent tos+l=−1.

3 Self-Similarity Transformations

By the dimensional analysis of Sedov,[13]the nondimensional variableηis defined by

whereλ=(2+m)/5 and the parametervis taken so thatηtakes the value 1 at the shock surface.This discloses thatη=r/R.The position of the inner expanding surface is given byη=ηp(=rp/R).

From relation(32),it follows that the motion of the shock front is described by the equation

From relation(33)it can be seen that the valuem=3 corresponds to uniform expansion of a cylindrical shock.Therefore,the solution of physical significance appears to be those for whichmlies in the range 0 to 3.

To obtain the similarity solutions,the field variables describing the flow pattern can be written in terms of the dimensionless functions ofηsuch that(Nath,[27]Nath and Takhar,[26]Vishwakarma and Pandey,[28]Nath[31])

whereV,ϕ,W,P,J,andDare functions ofηonly.

For the existence of similarity solutions“M∗” should be constant,therefore

Using the similarity transformations(34),the system of governing Eqs.(1)–(6)can be transformed and simplified to the following system of ordinary differential equations

where

Also,2δ+3q+s+1=0 was necessary to use to obtain the similarity solution.The quantityξis a constant taken as the parameter which characterizes the interaction between the gas and the incident radiation flux(Nath,[27]Nath and Takhar,[26]Khudyakov[24]).

Solving the above set of differential equations(36)–(41)for dV/dη,dD/dη,dP/dξ,dϕ/dη,dW/dη,and dJ/dξ,we obtain

where

Applying the similarity transformations(34)on Eqs.(12),we obtain the non-dimensional components of the vorticity vectorlr=ζr/(U/R),lθ=ζθ/(U/R),lz=ζz/(U/R)in the flow- filed behind the shock as

Using the self-similarity transformations(34),the shock conditions(26)are transformed into

whereσ=µwas necessary to use to obtain similarity solution.

At the inner boundary surface(piston)of the flow- filed behind the shock,the condition is that the velocity of the surface is equal to the normal velocity of the fluid on the surface.This kinematic condition from Eq.(34)can be written as

Normalizing the variablesu,v,w,ρ,Z,pandjwith their respective values at the shock,we obtain

4 Results and Discussion

The set of ordinary differential equations(43)–(48)have been integrated numerically with the boundary conditions(53)–(54)to obtain the distribution of flow variables between piston(η=ηp)and the shock front(η=1)by using the Runge–Kutta method of fourth order.Parameter of the inert mixture(glass or alumina Al2O3)are within the following range:dust particle size is of the order of 1µm–10µm(Higashino and Suzuki,[2]Fedrov and Kratova,[42]Nath,[12])the mass fraction(concentration)of solid particles in the mixture is varied fromKp=0 toKp=0.3 and the material density of solid particlesρsp=2.5 g/cm3.This case may be realized in an air flow with a suspension of alumina or glass particles.For the purpose of numerical integration,the values of the constant parameters are taken to be(Paiet al.,[1]Steiner and Hirschler,[16]Khudyakov,[24]Nath,[27]Vishwakarma and Pandey,[28]Miura and Glass[43])γ=1.4;β′=1;α=−1/2;q=0;s=1;δ=−1;M∗2=25;Kp=0,0.1,0.3;G0=1,10,100;ξ=0.01,0.1,0.5,1;m=1.5,2.0,2.5.The valuesγ=1.4,β′=1 may correspond to the mixture of air and glass particles(Miura and Glass[9]),andKp=0 correspond to the dust free case(the solution obtained by Nath[27]).The valueM∗=5 of the shock Mach-number is appropriate,because we have treated the flow of a pseudo- fluid(small solid particles)and a perfect gas at a velocity and temperature equilibrium.Our solution corresponds to the solution given by Nath[27]in dust free case.We have also considered the axial as well as azimuthal components of fluid velocity and components of vorticity vector(see Figs.1(c),1(g),1(h),and 2(c),2(g),2(h)).Also,our work corresponds to the solution given by Singh[30]in non-rotating dust case.Figures 1 and 2 show that the obtained solution is in good agreement with the existing solutions of Nath[27]and Singh.[30]

Table 1 shows the variation of density ratioβ(=ρ0/ρ1)across the shock front and the position of the inner expanding surfaceηpfor different values ofm,G0andKpwithα=−1/2;q=0;s=1;δ=−1;M∗2=25;γ=1.4;β′=1;ξ=0.1 in both the rotating and nonrotating cases.Table 2 shows the variation of density ratioβ(=ρ0/ρ1)across the shock front and the position of the inner expanding surfaceηpfor different values ofξandKpwithγ=1.4;β′=1;α=−1/2;q=0;s=1;δ=−1;M∗2=25;m=2.0 in both the rotating and non-rotating cases.Tables 1 and 2 show that the distance of the inner boundary surface from the shock front is less in the case of non-rotating medium in comparison with that in the case of rotating medium.Physically,it means that the gas behind the shock is less compressed in rotating medium i.e.the shock strength is decreased in rotating medium.

Table 1 The density ratio β across the shock and the position of the inner boundary surface ηpfor different values of Kp,G0and m with α =−1/2;q=0;s=1;δ= −1;ξ=0.1;M∗=5;γ=1.4;β′=1.

Fig.1 Variation of the reduced flow variables in the region behind the shock front(a)radial component of fluid velocity u/u1,(b)Azimuthal component of fluid velocity v/v1,(c)Axial component of fluid velocity w/w1,(d)Density ρ/ρ1,(e)Pressure p/p1,(f)Radiation flux j/j1,(g)Non-dimensional azimuthal component of vorticity vector lθ,(h)Non-dimensional axial component of vorticity vector lz:1.Kp=0,m=1.5;2.Kp=0,m=2.5;3.Kp=0.3,G0=1,m=1.5 4.Kp=0.3,G0=1,m=2.5;5.Kp=0.3,G0=10,m=1.5;6.Kp=0.3,G0=10,m=2.5.

Figures 1(a)–1(h)and 2(a)–2(h)show the variation of the reduced radial component of fluid velocityu/u1,the reduced azimuthal component of fluid velocityv/v1,the reduced axial component of fluid velocityw/w1,the reduced densityρ/ρ1,the reduced pressurep/p1,the reduced radiation fluxj/j1,the non-dimensional azimuthal component of vorticity vectorlθand the non-dimensional axial component of vorticity vectorlzagainst the simi-larity variableηfor different values of parametersm,G0,Kp;and with the parametersξ,Kprespectively.These two figures demonstrate that the flow variablesv/v1,ρ/ρ1,andj/j1decrease but the flow variablesw/w1,lz,andlθincrease as we move from the shock front to the inner expanding surface.

Fig.2 Variation of the reduced flow variables in the region behind the shock front(a)Radial component of fluid velocity u/u1,(b)Azimuthal component of fluid velocity v/v1,(c)Axial component of fluid velocity w/w1,(d)Density ρ/ρ1,(e)pressure p/p1,(f)Radiation flux j/j1,(g)Non-dimensional azimuthal component of vorticity vector lθ,(h)Non-dimensional axial component of vorticity vector lz:1.Kp=0,ξ=0.1;2.Kp=0,ξ=1.0;3.Kp=0.1,G0=10,ξ=0.1;4.Kp=0.1,G0=10,ξ=1.0.

From Tables 1,2 and Figs.1(a)–1(h),2(a)–2(h)it is found that the effects of an increase in the value of the mass concentration of solid particlesKpin the mixture are as follows:

(i)To decrease the value ofβi.e.to increase the shock strength;whereas the value ofβincreases i.e.the shock strength decreases forG0=1(see Tables 1,2);

(ii)To decreaseηpwhenG0=1,i.e.to increase the distance of the inner expanding surface from the shock front.Physically,it means that the gas behind the shock is less compressed,i.e.the shock strength is decreased;whereas reverse behaviour is observed whenG0=10,100;which is same as in(i)above(see Tables 1,2);

(iii)To increase the flow variableu/u1at any point in the flow- field behind the shock front(see Figs.1(a),2(a));

(iv) To increase the flow variablesv/v1,ρ/ρ1,andp/p1whenG0=1 but to decrease them in general forG0=10;whereas the reverse behaviour is obtained for flow variablesw/w1,lθ,lzandj/j1in the flow- field behind the shock front(see Figures 1(b)–1(h)and 1(b)–1(h)).

From Table 1 and Figs.1(a)–1(h)it is shown that the effects of an increase in the ratio of the density of the solid particles to the initial density of the gasG0are as follows:

(i)To decrease the value ofβi.e.to increase the shock strength(see Table 1);

(ii)To decrease distance of the inner boundary surface from the shock front,i.e.the flow- field behind the shock becomes denser.This illustrates same result as given in(i)above,i.e.to increase the shock strength(see Table 1);

(iii)To decrease the flow variablesu/u1,v/v1,p/p1,andρ/ρ1;but to increase the flow variablesw/w1,lθ,lz,andj/j1at any point in the flow- field behind the shock front(see Figs.1(a)–1(h)).

Table 2 The density ratio β across the shock and the position of the inner boundary surface ηpfor different values of Kpand ξ with α = −1/2;q=0;s=1;δ= −1;M∗=5;γ =1.4;β′=1,m=2.0.

The effects of an increase in the value of index for the time dependent energy law parametermare as follows:

(i) To increaseηp,i.e.distance between the inner boundary surface from and shock front decreases.This means that shock strength increases(see Table 1);

(ii)To increase the flow variablesp/p1,u/u1,lθ,lzandj/j1;but to decrease the flow variablev/v1,at any point in the flow- field behind the shock front(see Figs.1(a)–2(b),2(e)–2(h));

(iii) To increase the flow variableρ/ρ1near the shock but to decrease it near the inner boundary surface;whereas reverse behaviour is obtained for the flow variablew/w1in the flow- field behind the shock front(see Figs.1(c)and 1(d)).

From Table 2 and Figs.2(a)–2(h)it is found that the effects of an increase in the radiation parameterξare as follows:

(i)To decrease the value ofηpi.e.to decrease shock strength(see Table 2);

(ii)to decrease the flow variablesu/u1,w/w1,p/p1,j/j1,lθ,lz;but to increase the flow variablesv/v1,ρ/ρ1at any point in the flow- field behind the shock front(see Figs.2(a)–2(h)).

5 Conclusion

The present work investigates the self-similar flow behind a cylindrical shock wave propagating in a rotational axisymmetric dusty gas(a mixture of perfect gas and small solid particles)under the action of monochromatic radiation.On the basis of this work,one may draw the following conclusions:

(i)The shock strength decreases as well as distance between shock front and inner boundary surface increases when radiation parameterξincreases;however reverse behaviour is observed whenmandG0increase.

(ii)Mass concentration of solid particles in the mixtureKphas same effect on shock strength asξwhenG0=1.Also,Kphas same effect on shock strength asmwhenG0=10 or 100.

(iii)The distance of the inner boundary surface from the shock front is less in the case of non-rotating medium in comparison with that in the case of rotating medium.Physically,it means that the gas behind the shock is less compressed in rotating medium i.e.the shock strength is decrease in rotating medium.

(iv)An increase in the radiation parameterξdecreases the flow variablesu/u1,w/w1,p/p1,j/j1,lθ,lz;whereas reverse behaviour is observed in the case of the flow variablesv/v1,ρ/ρ1.

(v)An increase in the parametersξandmhas opposite behaviour on the flow variablesu/u1,v/v1,p/p1,j/j1,lθandlz.

(vi) An increase in the parametersξandKphas same behaviour on the flow variablesp/p1whenG0=10;whereas these parameters have opposite behaviour on the flow variablesu/u1,v/v1,w/w1,ρ/ρ1,j/j1,lθ,andlz.

(vii)An increase in parametersξandG0has opposite behaviour on the flow variablesv/v1,w/w1,ρ/ρ1,j/j1,lθ,andlz;however same behaviour is obtained for the flow variablesu/u1andp/p1.

The article concerns with the explosion problem in rotating medium,however the methodology and analysis presented here may be used to describe many other physical systems involving non-linear hyperbolic partial differential equations.The examples we have given make clear the nature of shock waves in rotating dusty gas under the action of monochromatic radiation.However,they serve mainly as illustrations of how the shock waves in dusty medium can be described.In reality,many other processes can be important and a more comprehensive analysis of the shock can be important for applications in astrophysics.The shock waves in a rotational axisymmetric dusty gas with monochromatic radiation and increasing energy can be important for description of shocks in supernova explosions and in the study of star burst galaxies,nuclear explosion,rupture of a pressurized vessel and explosion in the ionosphere etc.Other potential applications of this study include analysis of data from exploding wire experiments in dusty medium,and cylindrically symmetric hypersonic flow problems associated with meteors or reentry vehicles(c.f.Hutchens,[44]Nath[37]).Also,the present study can be important for the description of the following:

5.1 Shocks in Supernova Explosions

The layer of dust behind the supernova shock is observed usually.The problem is to verify whether the layer of dust is related to the process of dust condensation behind the shock wave front.

5.2 Shocks in Intense Prolonged Flare Activity

The present self-similar model may be used to describe some of the overall features of a “driven”shock wave produced by a flare energy releaseE(c.f.Eq.(28))that is time dependent.The energy“E”increases with time and the solutions then correspond to a blast wave produced by intense,prolonged flare activity in a rotating star when the wave is driven by fresh erupting plasma for some time and its energy tends to increase as it propagates from the star.

[1]S.I.Pai,S.Menon,and Z.Q.Fan,Int.J.Eng.Sci.18(1980)1365.

[2]F.Higashino and T.Suzuki,Z.Naturforsch.35a(1980)1330.

[3]W.Gretler and R.Regenfelder,Eur.J.Mech.B/Fluids 24(2005)205.

[4]S.I.Popel and A.A.Gisko,Nonlinear Process.Geophys.13(2006)223.

[5]O.Igra,G.Hu,J.Falcovitz,and B.Y.Wang,Int.J.Mult.Flow 30(2004)1139.

[6]M.Sommerfeld,Exper.Fluids 3(1985)197.

[7]T.Elperin,G.Ben-Dor,and O.Igra,Int.J.Heat Fluid Flow 8(1987)303.

[8]H.Miura,Fluid Dyn.Res.6(1990)251.

[9]H.Miura and I.I.Glass,Proc.Roy.Soc.Lond.397A(1985)295.

[10]G.Nath,Indian J.Phys.90(2016)1055.

[11]G.Nath and J.P.Vishwakarma,Acta Astronaut.128(2016)377.

[12]G.Nath,Astrophys.Space Sci.361(2016)1.

[13]L.I.Sedov,Similarity and Dimensional Methods in Mechanics,Academic Press,New York(1959).

[14]V.P.Korobeinikov,Proceedings of the Steklov Institute of Mathematics,119,American Mathematical Society,Providence(1976).

[15]S.I.Pai,Two Phase Flows,Vieweg Tracts in Pure and Applied Physics,Vol.3,Braunschweig:Vieweg-Verlag,(1977)[Chapter V].

[16]H.Steiner and T.Hirschler,Eur.J.Mech.B/Fluids 21(2002)371.

[17]J.P.Vishwakarma and G.Nath,Phys.Scri.74(2006)493.

[18]R.E.Marshak,Phys.Fluids 1(1958)24.

[19]L.A.Elliott,Proc.Royal Soc.London Series A:Mathematical and Physical Sciences 258(1960)287.

[20]K.C.Wang,J.Fluid Mech.20(1964)447.

[21]J.B.Helliwell,J.Fluid Mech.37(1969)497.

[22]J.R.NiCastro,Phys.Fluids 13(1970)2000.

[23]G.Deb Ray and J.B.Bhowmick,Ind.J.Pure Appl.Math 7(1976)96.

[24]V.M.Khudyakov,Sovit.Phys.Dokl.Trans.American Institute of Physics 28(1983)853.

[25]A.N.Zheltukhin,Geophys.Astrophys.J.Appl.Math.Mech.52(1988)262.

[26]O.Nath and H.S.Takhar,Astrophys.Space Sci.166(1990)35.

[27]O.Nath,IL Nuovo.Cimento.D 20(1998)1845.

[28]J.P.Vishwakarma and V.K.Pandey,Appl.Math.2(2012)28.

[29]G.Nath and P.K.Sahu,Ain Shams Eng.J.(2016)DOI 10.1016/j.asej.2016.06.009.

[30]K.K.Singh,Int.J.Appl.Math.Mech.9(2013)37.

[31]G.Nath,Advan.Space Res.47(2011)1463.

[32]G.Nath,Ain Shams Eng.J.3(2012)393.

[33]G.Nath,Meccanica 50(2015)1701.

[34]V.A.Levin and G.A.Skopina,J.Appl.Mech.Tech.Phys.45(2004)457.

[35]H.A.Zedan,Appl.Math.Comput.132(2002)63.

[36]G.Nath,Res.Astr.Astrophys.10(2010)445.

[37]G.Nath,Shock Waves 24(2014)415.

[38]Y.B.Zel’dovich and Y.P.Raizer,Physics of Shock Waves and High Temperature Hydrodynamic Phenomena,Vol.II.Academic Press,New York(1967).

[39]P.Chaturani,Appl.Sci.Res.23(1970)197.

[40]M.N.Director and E.K.Dabora,AIAA J.15(1977)1315.

[41]M.H.Rogers,Quarterly J.Mech.Appl.Math.11(1958)411.

[42]A.V.Fedorov and Y.V.Kratova,Heat Transf.Res.43(2012)123.

[43]H.Miura and I.I.Glass,Proc.R.Soc.Lond.A 385(1983)85.

[44]G.J.Hutchens,J.Appl.Phys.77(1995)2912.