面向移动设备的图像匹配算法适用性研究
黄碧辉 吴 勇,2* 郑森源
(1.福建师范大学 地理科学学院,福建 福州 350007;2.福建省陆地灾害监测评估工程技术研究中心,福建 福州 350007)
增强现实(Augmented Reality,AR)是一种在用户通过设备观察到的现实世界中添加由计算机生成的多媒体对象和3D模型等虚拟信息的技术,通过这种虚实结合场景给用户带来对现实世界新的认知[1].高效、精准的移动增强现实系统研究受到国内外众多学者的关注,其中图像匹配技术是其核心的研究内容.相比桌面端电脑,移动终端由于其便携性,能更好地扩大增强现实系统的应用场景,使用户与现实世界有更多的互动.图像匹配算法在室内移动增强现实的应用已经较为成熟,但是在室外大场景下,光照、视角、尺度、旋转等因素容易影响匹配效果.因此,当前移动增强现实迫切需要解决的问题是在保证室外匹配精度的条件下,实现目标快速高效的匹配.图像匹配算法可分为基于像素灰度和基于图像特征两大类[2].其中,基于像素灰度的匹配方法是利用图像像素之间的灰度差寻找对应图像,缺点在于计算量大、实时性较差,且对图像光照变化、灰度畸变和几何变形较敏感,易造成较大的匹配误差;而基于图像特征的匹配方法是利用图像特征寻找对应图像[3],其算法具有图像匹配性能优秀和简单易操作、运算量小等优点.在基于图像特征的匹配研究中,Lowe于2004年提出了尺度不变特征变换(Scale Invariant Feature Transform,SIFT)图像特征点匹配算法,该算法对图像的各种变换具有较强的鲁棒性,能较好解决匹配过程中图像变形等问题,且该算法特征点数量多、信息量大、可拓展性强[4],已被广泛应用于目标识别、图像配准、数据挖掘、机器人导航等领域.随着对特征点匹配算法匹配速度要求越来越高,许多算法相继被提出.如Bay等在2006年提出SURF(Speeded Up Robust Features)算法[5],采用积分图像和HESSIAN矩阵技术,有效地降低SURF算法的运算量;Rublee等于2011年提出ORB(Oriented FAST and Rotated BRIEF)算法[6],其在计算性能上有较大的提升,克服了SIFT和SURF算法实时性不强的缺陷;2011年,Stefan等提出BRISK(Binary Robust Invariant Scalable Keypoints)算法[7],该算法具有较高的特征定位精度和较好的尺度、旋转、噪声的鲁棒性,但对光照变化不敏感[8];2012年Alahi等提出具有视网膜成像特性的FREAK(Fast Retina Keypoint)描述子算法[9],其计算速度较SIFT、SURF算法更有优势,且在图像光照、旋转、视角等变换上具有较强的鲁棒性[10];在综合传统优秀图像匹配算法的基础上,通过融合改进产生了FAST_FREAK、FAST_SURF、SURF_FREAK等混合算法.现有的研究多是针对电脑终端算法实现以及鲁棒性而言的,而对性能较弱、室外环境因素影响更强的移动终端实现图像匹配的鲁棒性、适用性等方面探讨较少.
基于此,本文以移动终端为实验平台,在常用的图像匹配算法实现的基础上,从匹配性能、旋转、光照、尺度、视角变换等方面进行算法效率与鲁棒性比较分析,探讨算法在移动终端上的适用性,以期为移动增强现实图像匹配应用提供参考.
1 实验方案及数据
1.1 实验方案
基于移动终端的图像匹配不仅受限于终端硬件性能,受室外环境因素影响也较大,对算法的实时性与匹配准确性要求较高.本实验以Eclipse和OpenCV2.4.9为开发平台,在vivo V3L型号1.5GHz八核处理器、3G内存的移动手机平台进行实验.实验选取了ORB、BRISK、SURF、SURF_FREAK、FAST_SURF、FAST_FREAK六种算法,从匹配速度、算法鲁棒性两个方面分别对匹配性能和稳定性进行对比分析,并根据指标的重要性与性能排名进行打分评价该算法的综合性能,选取适用于移动终端的图像匹配算法.具体实验流程如图1所示.

图1 图像匹配算法实验流程图Fig. 1 Basic flow chart of the image matching algorithms
其中,匹配性能主要通过匹配速度指标进行衡量,该匹配速度是指特征点检测、描述符提取和特征匹配的综合耗时.稳定性采用旋转、尺度、光照和视角四种变换图像下提取的正确匹配点对与匹配分数两个指标进行衡量.正确匹配点对体现该算法对图像匹配检测的性能,匹配点对数量越多,匹配效果越好.匹配分数是指两幅匹配图像中筛选出的正确匹配点对与两幅匹配图像中提取出的较少特征点数量之比,用于衡量各类算法对于各种图像变换的不变性,值越大表示区域检测器的鉴别能力越好.匹配分数的计算公式如下:
(1)
式(1)中:rm为匹配分数,N为两幅图像中提取出的正确匹配点对数量,n1和n2表示在两幅待匹配图像上的相同区域内分别检测出的特征点数量,min(n1,n2)为n1和n2的较小值.
1.2 实验步骤与数据

图2 室外场景测试图Fig.2 Building scene image for experiment
移动增强现实利用图像匹配算法进行目标物体识别,其具体识别步骤如下:第一步,通过摄像头获取真实场景视频流,通过图像匹配算法与存储在手机的目标图像进行匹配,检测其中是否含有匹配的目标图像;第二步,如果不存在匹配的目标图像,则重复第一步,如果存在匹配的目标图像,则计算目标图像的旋转和平移矩阵,即投影变换矩阵;第三步,根据投影变换矩阵实时调整虚拟模型的姿态,将虚拟模型绘制到屏幕上.
本实验选取多个建筑场景的图像数据,用于测试算法的鲁棒性.图2所示为其中一个场景,由四组建筑物场景图像构成,每组均为六幅图像.第一组为旋转变换实验图像,由一张基准图像以18°为间隔逆时针旋转至90°生成;第二组为尺度实验图像,以距离建筑物40 m为基准,按图像尺度缩小间隔0.2倍采集获取;第三组为光照实验图像,将基准图像的亮度按16%进行递减获得;第四组为视角变换实验图像,以距离建筑物40 m为半径,每间隔12°拍摄一张图像直至60°.
2 实验结果与分析
2.1 匹配速度对比
对于处理能力较弱的移动终端而言,匹配算法运行时间是评价算法适用性的首要指标,其运行效率直接影响用户对增强现实应用的体验.各算法图像匹配耗时统计结果如表1所示.

表1 各算法图像匹配耗时统计结果
从表1匹配点对数量看,SURF_FREAK和SURF算法检测的匹配性能优于其他算法.由于这两个算法在特征点检测和描述符提取上具有强烈方向性和亮度性的特性,使其匹配效果较好,但同时也较大程度影响算法的运行效率.从运行效率上看,FAST_FREAK和ORB算法分别耗时571 ms和640 ms,算法的实时性较好,原因是FAST_FREAK、ORB算法采用了改进的FAST算法以及二进制描述符,该方法处理和匹配速度更快,能较好地满足移动增强现实应用实时性的要求.
2.2 旋转变换测试
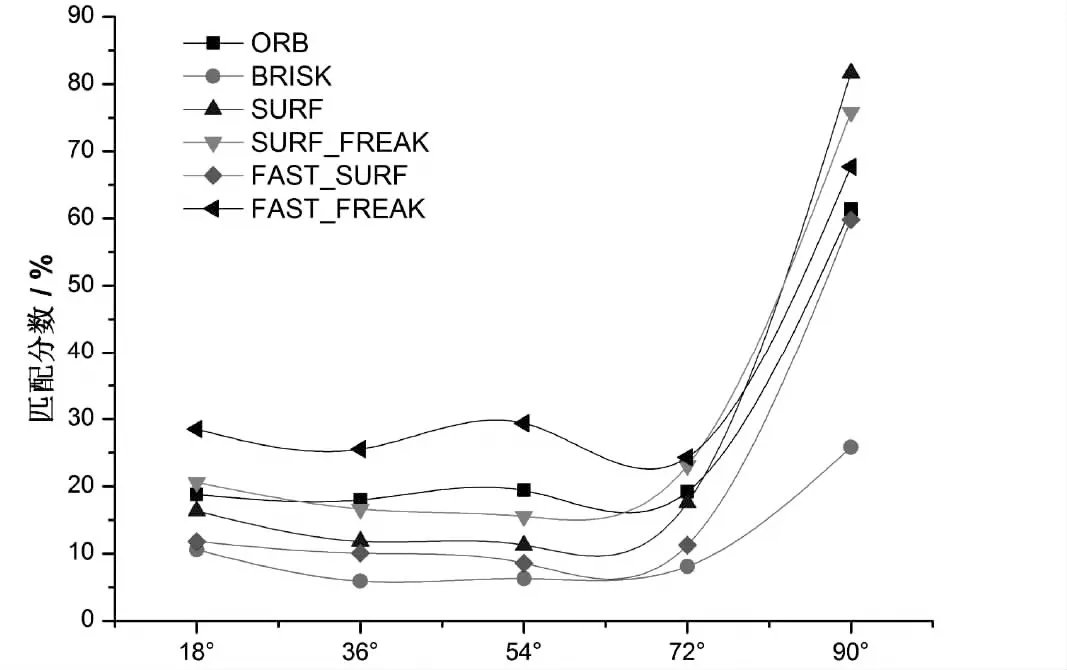
旋转变换角度图3 旋转变换的匹配分数曲线Fig. 3 The matching score cures with rotation change
旋转变换匹配点对与匹配分数测试结果如图3、表2所示.各匹配算法在图像旋转36°、54°左右时,匹配点对数量下降幅度最大,但是在图像旋转接近90°时,匹配点对数量快速回升.同样,匹配分数曲线呈现先下降再上升的趋势.这主要是由于在旋转变换过程中,匹配图像的像素点绕着旋转中心发生相应角度的旋转,导致在旋转变换前图像的关键点周边提取的像素梯度值和关键点方向信息发生了改变,改变了原图像特征点的主方向,从而降低了图像匹配的精度.

表2 各算法旋转变换匹配点对测试结果
注:“a to a”表示旋转变换照片集中照片a与照片a图像匹配,其它类似.

图4 尺度变换的匹配分数曲线Fig. 4 The matching score cures with scale change
在旋转变换中,FAST_FREAK和SURF_FREAK在匹配点对数量和匹配分数上都表现出较强的鲁棒性,原因是FREAK描述符采样结构中采样点对具有较强的对称性.将表2和图3的数据进行比较,虽然SURF算法匹配点对数量较ORB多,但是SURF匹配分数曲线值整体上低于ORB算法,且匹配点对的数据相较ORB波动性较大,因此SURF旋转鲁棒性较ORB差.造成这一结果的主要原因是SURF算子使用矩形邻域的梯度计算特征向量,与ORB采用oFAST特征检测算子相比,其受旋转角度变化影响较大.
2.3 尺度变换测试
尺度变换匹配点对与匹配分数测试结果如图4、表3所示.各种算法的匹配点对和匹配分数整体呈下降趋势,而SURF_FREAK和SURF在下降过程中出现小幅上升.原因在于变换程度越大的图像,越容易产生新的特征点,造成其特征点落在原图像区域的特征点数量减少,导致因图像正确匹配点对数量的减少而影响算法的性能.

表3 各算法尺度变换匹配点对测试结果
注:“a to a”表示光照变换照片集中照片a与照片a图像匹配,其它类似.
SURF和SURF_FREAK算法在匹配点对数量和匹配分数上都表现出较强的鲁棒性.其中,SURF_FREAK算法尺度鲁棒性最强,FREAK算法描述符的采样位置和半径随着尺度变化,加强了采样点距离之间的联系.将表3和图4的数据进行比较,ORB的尺度鲁棒性高于BRISK、FAST_FREAK和FAST_SURF,主要的原因是ORB采用改进的FAST算法,建立金字塔,利用机器学习方法选取出最优关键点,解决了FAST的特征点不具备尺度不变性的问题.
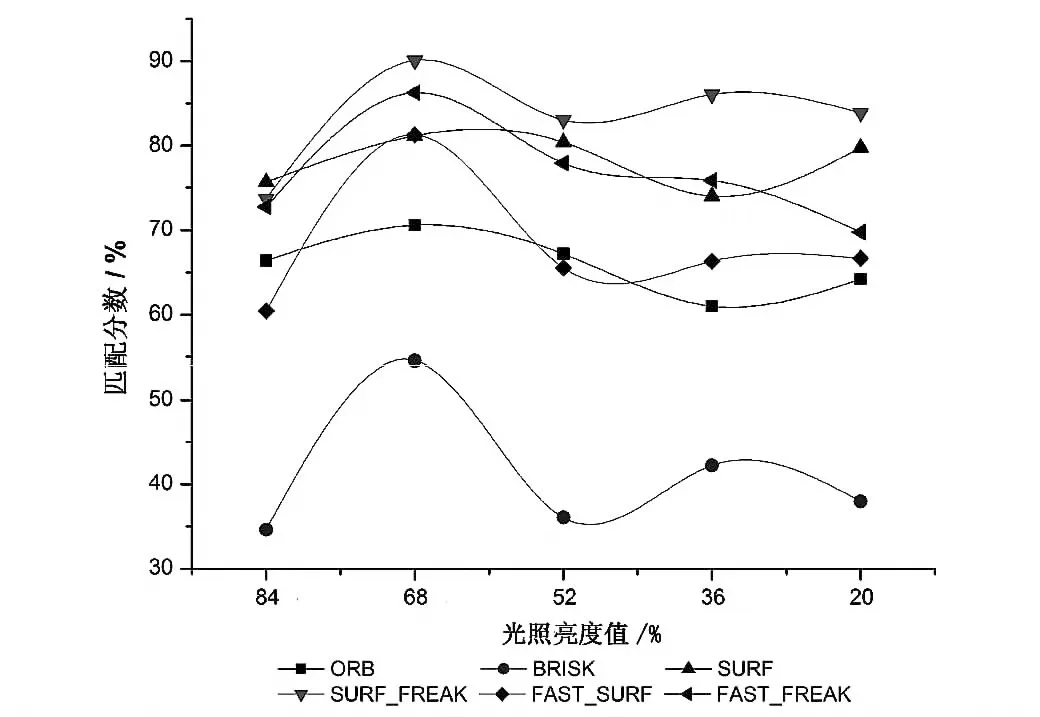
图5 光照变换的匹配分数曲线Fig. 5 The matching score cures with illumination change
2.4 光照变换测试
光照变换匹配点对与匹配分数测试结果如图5、表4所示.匹配点对数量对光照影响较为敏感,匹配点对数量随着光照亮度下降而减少,原因在于两幅图像同一位置的像素块可能受不同光照影响而有不同的灰度值,造成匹配过程中部分特征点被强化、部分特征点被弱化,最终使得一些相同特征点位于不同灰度阶中,从而影响图像匹配精度.相比其它算法,SURF_FREAK和SURF匹配点对数量较多,匹配分数得分较高,匹配质量较好.SURF_FREAK算法光照鲁棒性较强,因为FREAK对高斯平滑后的采样点对的灰度值进行对比,比SURF利用邻近像素块的灰度差建立的描述子更具统计性.而BRISK算法在匹配点对和匹配分数这两个方面的表现明显较差,光照鲁棒性最差.图中ORB的匹配分数曲线与FAST_SURF多次相互交叉,但当光照变换至20%时,ORB算法的匹配点对数量远大于FAST_SURF算法,因此ORB算法的光照鲁棒性优于FAST_SURF算法.
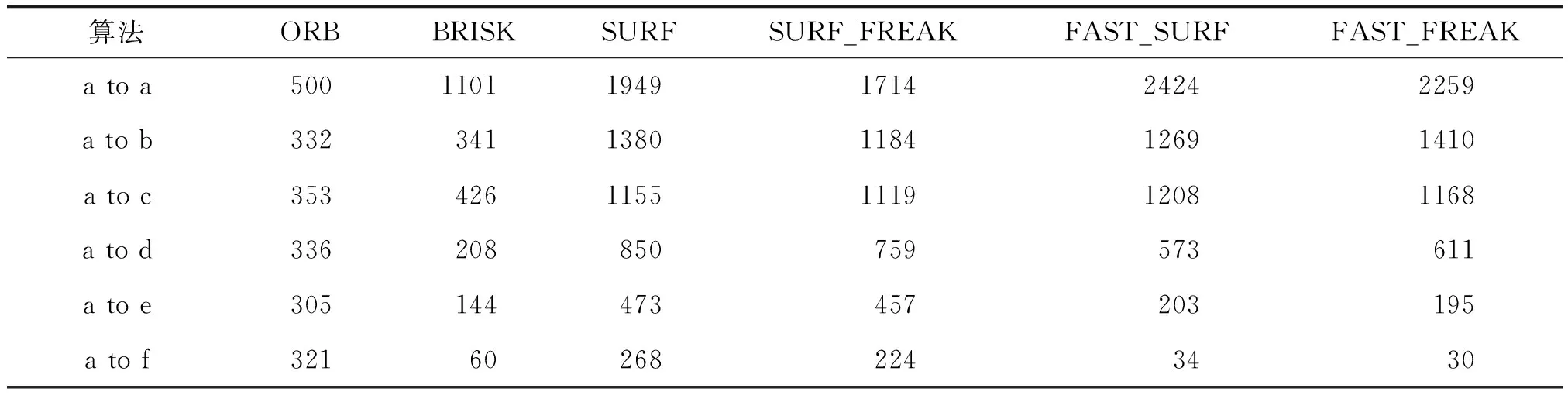
表4 各算法光照变换匹配点对测试结果
注:“a to a”表示视角变换照片集中照片a与照片a图像匹配,其它类似.
2.5 视角变换测试

图6 视角变换的匹配分数曲线Fig. 6 The matching score cures with viewpoint change
视角变换匹配点对与匹配分数测试结果如图6、表5所示.视角变换对匹配精度产生较大影响,图像视角变化越大匹配点对数量和匹配分数值下降幅度越大,原因在于视角变化越大原始图像处于边缘和外部的特征点保留得越少,且视角变换越大特征点描述符形变越大,最终导致算法匹配精度下降.相比其他算法,SURF_FREAK和SURF匹配点对数量较多,匹配分数得分较高,视角变换的鲁棒性较好.而BRISK的匹配点对数量少,且匹配分数值较低,BRISK视角变换的鲁棒性最差.虽然ORB匹配点对数量少,但是数据波动小.从匹配分数上看,ORB在视角变换程度较小时,得分比BRISK、FAST_FREAK和FAST_SURF大,甚至一度比SURF和SURF_FREAK得分高,因此ORB算法在视角变换中表现出较强的鲁棒性.

表5 各算法视角变换匹配点对测试结果
注:“a to a”表示视角变换照片集中照片a与照片a图像匹配,其它类似.
2.6 图像匹配算法性能综合评价

图7 各图像匹配算法综合性能图Fig. 7 Comprehensive performance chart of each image matching algorithm
按照上述性能指标测试结果,根据各算法在速度、旋转、尺度、光照和角度五项指标排名先后顺序进行评分,每个排名间隔1分,制作算法综合性能图,如图7所示.
总体上看,各种匹配算法在匹配效率与鲁棒性方面各有优缺点,没有一种算法在上述两个指标上同时存在明显优势.对于面向自然场景的移动增强现实应用而言,图像匹配速度是其应用考虑的首要因素,直接影响应用的可接受程度.其次,室外环境下光照、视角等因素也较大程度的影响图像匹配的精度,且各种指标的重要程度不一致.因此,利用专家打分法赋予速度、光照、视角、旋转和尺度五项指标不同权重系数,其相应权重系数分别为0.5、0.15、0.15、0.1、0.1.各算法的综合得分由图7中五项指标的排名得分与其对应权重系数相乘后累加获得.经计算,ORB、BRISK、SURF、SURF_FREAK、FAST_SURF、FAST_FREAK算法的综合得分分别为4.35、2.35、2.8、3.9、2.75、4.85.虽然ORB算法性能综合评价得分低于FAST_FREAK算法,但其匹配速度与FAST_FREAK算法仅相差68 ms,且ORB算法对于各种图像变换的鲁棒性表现得更为均衡,更适用于移动增强现实的应用.
3 结论
本文基于移动终端对图像匹配算法的运行效率与图像变换的鲁棒性进行比较分析,并从综合角度探讨图像匹配算法在移动终端上的适用性以及室外复杂环境的鲁棒性.实验结果表明,ORB算法具有较高的运行效率,同时其在旋转、光照、尺度、视角等变换上具有较好的鲁棒性,相比SURF_FREAK、SURF、BRISK、FAST_SURF等图像匹配算法在移动终端上具有明显优势,且算法简单易于实现,适用于移动增强现实应用.由于ORB算法在尺度和视角变换测试中匹配点对较少,下一步将考虑借鉴 SIFT尺度空间理论求取特征点的质心方向,并采用分块采样模式取代整图像块采样模式,以提高ORB算法在尺度和视角变化上的鲁棒性,并将它应用于室外移动增强现实中.
[1] 罗斌,王涌天,沈浩,等.增强现实混合跟踪技术综述[J].自动化学报,2013,39(8):1185-1201.
[2] 汪松.基于SIFT算法的图像匹配方法研究[D].西安:西安电子科技大学,2013.
[3] 罗楠,孙权森,耿蕾蕾,等.一种扩展SURF描述符及其在遥感图像配准中的应用[J].测绘学报,2013,42(3):383-388.
[4] Lowe D G.Distinctive image features from scale invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[5] Bay H,Ess A,Tuvtellars T,et al.Speeded-up robust features(SURF)[J].Computer Vision and Image Understanding,2008,110(3):346-359.
[6] Rublee E,Rabaud V,Konolige K,et al.ORB:an effcient alternative to SIFT or SURF[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision.Barcelona,2011:2564-2571.
[7] Stefan L,Margarita C,Roland Y S.BRISK:binary robust invariant scalable keypoints[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision(ICCV).Barcelona,2011:2548-2555.
[8] 林森,苑玮琦,宋辉.二进制鲁棒不变尺度特征在非接触掌纹识别中的应用[J].仪器仪表学报,2013,34(12):2785-2792.
[9] Alahi A,Ortiz R,Vandergheynst P.FREAK:fast retina keypoint[C]//Proceedings of the 2012 IEEE Conference on Computer Version and Pattern Recognition. Providence,2012:510-517.
[10] 王灿进,孙涛,陈娟.基于FREAK特征的快速景象匹配[J].电子测量与仪器学报,2015,29(2):204-212.

