冲积河流沙质河床推移质级配分布规律

张罗号，张红武，赵晨苏

（1.河海大学 水利水电学院，江苏 南京 210098；2.清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084；3.北京科技大学 土木与资源工程学院，北京 100083）

1 问题的提出

随着河流水沙数学模型的不断发展，推移质级配的研究受到广泛关注，但现有研究成果无论在计算精度方面还是在天然河流的适用性上尚不完善，主要原因在于推移质级配不仅同河床泥沙组成密切相关，且在一定水流条件下与悬移质泥沙交换频繁，推移质泥沙的运动机理十分复杂［1］。

冲积河流沙质河床中，随着水流条件增强，河床表面可动泥沙的数量也逐渐增多，并以推移状态运动成为推移质泥沙，其中细颗粒还会进一步转化为悬移质泥沙，此时推移质级配常与床沙较为接近［2］。图1给出了长江汉口水文站推移质泥沙及床沙取样级配曲线的比较结果，尽管受采样方法的差异及颗分精度所限，但由该图仍可看出，沙质河床上推移质泥沙级配同床沙组成分布状况颇为相近。

图1 沙质河床推移质泥沙与床沙级配实测数据的比较

因此，一些学者通过修正床沙级配得到确定推移质级配的半经验方法。具有代表性的研究成果包括李昌华［3］通过将床沙级配中不动泥沙的百分数扣除并标准化后得到的推移质级配公式，被称为“最大粒径法”；以及张红武［4］采用推移质泥沙平均粒径与床沙平均粒径之比修正床沙级配曲线，得到一条与床沙级配曲线平行的推移质级配曲线，被称为“平均粒径类比法”。这类方法所建立的模式直观、计算较为简便，但其缺点是基本没有考虑水流泥沙运动同推移质级配变化的内在联系。

Gessler［5］根据统计理论对不同粒径级下的泥沙的起动概率进行了研究，得到推移质级配计算式为：

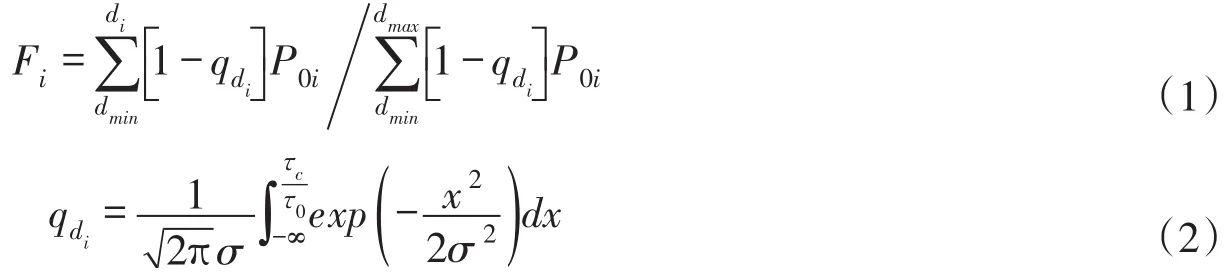
式中：P0i为床沙中第i粒径组所占沙重百分数；Fi为推移质中粒径小于di的沙重百分数；qdi为粒径为di泥沙的不动概率；τ0为河床床面水流拖曳力；σ为拖曳力脉动值的标准差；τc为第i粒径组的泥沙起动临界拖曳力；x=τ0/τc为积分变量。

上式中泥沙起动条件由均匀沙Shieleds曲线确定［6］，为将该方法延用到非均匀沙中，后来学者通过研究得到了类似公式，如董永华［7］考虑了非均匀沙起动特点；张启卫［8］假设了床沙转化为推移质泥沙的条件为作用于泥沙颗粒的瞬时底速大于临界起动流速。此类方法存在的最大局限是必须已知床沙级配曲线，而水文站每年床沙实测资料十分有限，且大部分水文站没有该项测量内容，无法取得床沙与推移质泥沙级配同步资料，很难适应不断变化的推移质级配的确定。

若直接从物理概念考虑，推移质级配与不同分组粒径的输沙数量相关。其中研究成果包括，乐培久［9］通过建立非均匀沙输沙率公式得到推移质级配计算公式：

式中：gbi为di粒径分组下的均匀沙推移质输沙率。但由于推移质输沙率测验精度低而使现有公式多不适用于典型沙质河床［2］，故必然导致此类方法建立的公式精度得不到保证。

目前，对挟沙水流中水流紊动作用推移质泥沙的规律尚无定论，但从推移质级配影响因素分析而进行的理论探讨很多。Diplas［10］通过分析泥沙颗粒所受水流作用力大小与作用时间等非恒定因素，并引入冲量的概念来描述推移质泥沙颗粒运动规律。张红武［11］根据随机理论分析了粗沙河床表面紊动特性和推移质泥沙颗粒的关系，建立了粗颗粒推移质泥沙级配公式。张绪进［12］、陆永军［13］在大量实测资料基础上，对推移质级配与床沙组成、水沙条件之间的关系进行了探讨。此外，何文杜［14］提出了平衡输沙条件下推移质最大粒径的确定方法。这些基于水力学及河流动力学建立的计算方法在理论与使用上都有一定价值，但多数公式结构过于复杂，其中部分参数还需要通过实测资料率定，计算精度也难以保证，且除张红武公式外，其余均是把推移质级配同床沙组成建立关系，一般仅适用于粗颗粒河床，尤其目前沙质河床推移质级配曲线更无理论性强且能够反映水流运动对推移质颗粒组成有直接影响的计算公式。为此，本文在分析近壁紊动源区内泥沙运动临界图景的基础上，对沙质推移质级配分布的表达形式进行了理论探讨。

2 推移质级配计算方法

2.1 沙质河床近壁泥沙运动的临界图形我们知道，被概化为二维均匀流的冲积河流，其紊动源区主要集中在近底由泥沙颗粒组成的床面附近［15］。因受某种扰动或同近壁区大流速梯度和强剪力相联系的压力差的作用，不断产生以高频率、小尺度紊动为主的紊动涡体，这些涡体逐渐离开河底上升扩散至全流区，从而床面附近即成为被L.Prandtl称之为“涡体作坊”的近壁紊动源区［16］。天然沙质河床的河流，正是在该区实现河床泥沙与水流相互作用、相互影响的，导致河床组成的不断调整或变化。

泥沙学者将跳跃作为沙质推移质运动的普遍形式，亦即沙质河床近壁紊动源区的泥沙一旦起动或被水流带离床面，随即可能跳起，以跳跃为主要运动形式，且与悬移质泥沙存在着相互交换。于是，沙质床面颗粒在近壁运动的临界图景可概括为：近底流区床面颗粒被具有瞬时垂向紊动速度的水流带离床面而起跳，至最大高度后的回落过程中，或在重力作用下以沉速下落，继续留在床面；或被路经此地的涡体卷走而离开本床面。

由于垂向紊动速度是一个瞬时量，以往研究从动力学或运动学观点出发建立平衡方程式都是不严格的［17］。鉴于动量是一个瞬时量，且适用于从微观角度审视紊动流速场与泥沙颗粒的关系，故在具有水流同泥沙相互作用过程的任何一个瞬间，用该物理量来分析近底颗粒沉浮的临界条件是合适的。跃动的泥沙在重力作用下以沉速下落的瞬间，如果在垂向遇到相同动量的紊团的对撞，即形成相对的平衡，故维持临界平衡的条件是具有瞬时垂向紊速vb的紊团向上的动量等于具有沉降速度ω的泥沙向下的动量。故沿垂向运用动量对撞平衡原理，可将决定近底颗粒沉浮的临界条件表示为：

式中：m1、m2分别为水流与泥沙相应的质量。

式（3）之所以对紊动流速引入绝对值符号，系考虑到泥沙沉速为大于零的数值（实际上，沉速方向向下，只有方向向上的垂向紊速对泥沙的作用才有效）。在连续介质条件下，向上紊动涡团与下沉泥沙颗粒的体积应该相同，如果以γ、γs分别代表水与泥沙的容重，m1、m2对应的密度即分别为γ/g、γs/g，式（3）可表示为：

一般情况下天然沙容重γs是水流容重γ的2.7倍，因此上式表明，沙质河床近底颗粒沉浮的临界条件是水流的瞬时紊动流速等于2.7倍泥沙在水中的沉速，而非两者相等，同运用动力学观点出发建立的平衡方程式也有差异。

2.2 推移质级配公式由于垂向瞬时紊动流速具有高斯分布性质［18］，故可给出其概率分布为：

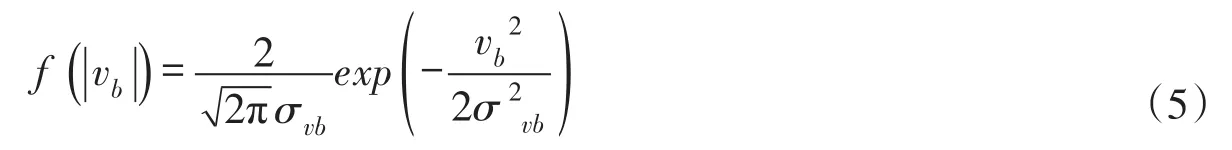
式中：σvb为垂向紊动强度。一般正态分布密度的系数分子为1，上式为2是由于瞬时紊速分布只取垂直向上部分；假定向上、向下两部分的分布相同，也是因为向上部分对泥沙的作用才有效。

由于沙质河床泥沙粒径一般为0.05～2 mm， 范围涉及过渡区和滞流区，而采用现有沉速公式尚不能直接推求出粒径的显式，张罗号等［19］利用量纲和谐原理及前人资料，得到如下包括了粒径范围为D=0.006～0.9 mm的沉速公式：

式中：ν为运动黏滞系数，m2/s。

将式（6）代入式（4），并写成随机方程：

根据概率分布函数计算公式，首先有：

可求出推移质粒径D的分布密度函数：

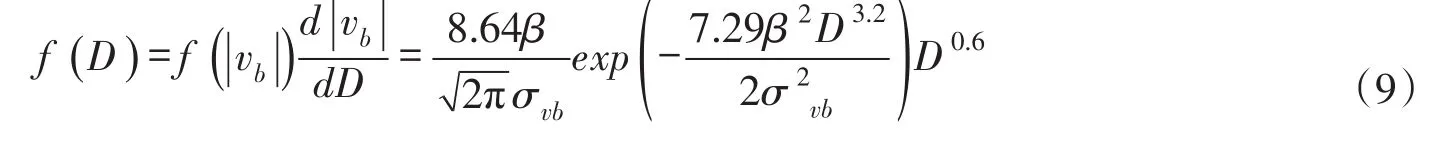
数学期望：

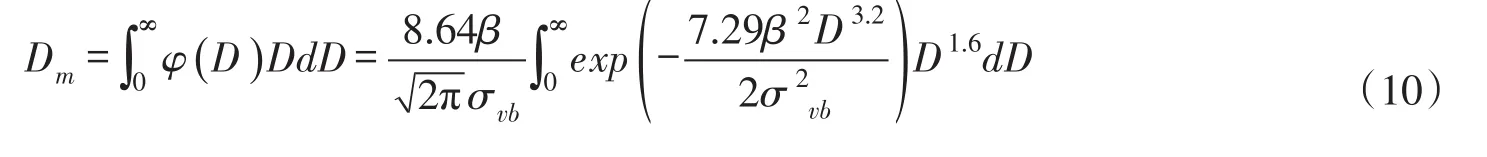
均方根为：

确定了上述关系式后，可研究推移质组成分布与垂向紊动流速分布的依存关系。以小于某粒径Di的泥沙数目所占泥沙总数的百分比表示级配曲线（这种方法对于沙质河床，所得结果与重量百分比法基本接近），从概率论的观点来看，即为：

将式（9）代入上式，可得：

由于被积函数式（13）中参数β及垂向紊动强度σvb均为定值，故可由矩形法或梯形法在（0，Di）区间内进行数值积分计算。对于垂向紊动强度，采用如下计算公式［20］：

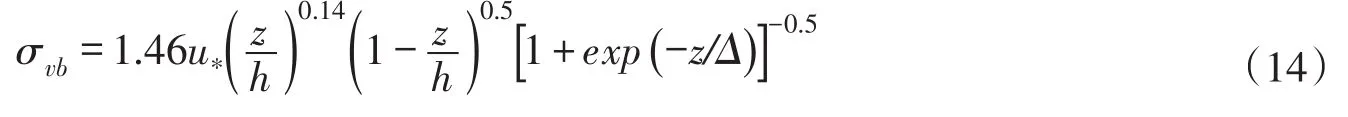
式中：u*为摩阻流速，m/s；由公式计算；h为水深，m；J为水面比降；z为以河底作为起始点的水深坐标，m；Δ为壁面粗糙度，m。

对于粗糙度Δ，本文根据前苏联学者Shevelev［21］的试验成果及张红武等近些年的试验资料［22］，得出糙率n与粗糙度Δ的关系式，即可用实测资料中易得到的糙率值进行计算：

通过资料验证表明，在天然河流常见水深范围内，可利用式（15）求出各河段糙率对应的粗糙度。若水深大于5 m且糙率大于0.016，则由卡门紊流粗糙区沿程损失系数公式、达西-魏斯巴赫公式与谢才-曼宁公式［23］联立求解，得到的下列关系式计算：

式中：R为水力半径，m。

当壁面粗糙度Δ数值很小时不属于紊流粗糙区，故不利用式（16）计算。

综上所述，在具体计算时取河流近底区z=3Δ，即可由式（14）—（16）求出不同水流条件下的近底紊动强度σvb，随后由式（9）得到推移质级配分布。

3 公式的检验

为验证本文推移质级配分布公式在冲积河流沙质河床的适用性，采用黄河上游及下游大量实测资料，对本文公式进行系统的计算比较（见图3—图4）。

由前文图1表明，沙质河床中推移质泥沙级配与河床表层床沙颗粒组成资料较为接近，故将缺少推移质级配实测资料的黄河上游主要取样断面，利用床沙取样资料代替。表1列举出黄河宁蒙河段干流所选取的重要河段河槽取样断面位置情况［24］，以及河槽表层及河槽深层泥沙颗粒分析结果中河床泥沙平均粒径Dcp与中值粒径D50。由表2也可看到，本文所选取的黄河宁蒙河段主要断面的床沙组成分布较为均匀，表明推移质泥沙与床沙掺混较频繁。黄河下游均采用推移质级配实测资料，由于缺少同步实测水文资料，故选用对应水文站/断面的月平均水力因子（见表2）。

表1 黄河宁蒙河段实测床沙平均粒径dcp与中值粒径d50数据比较

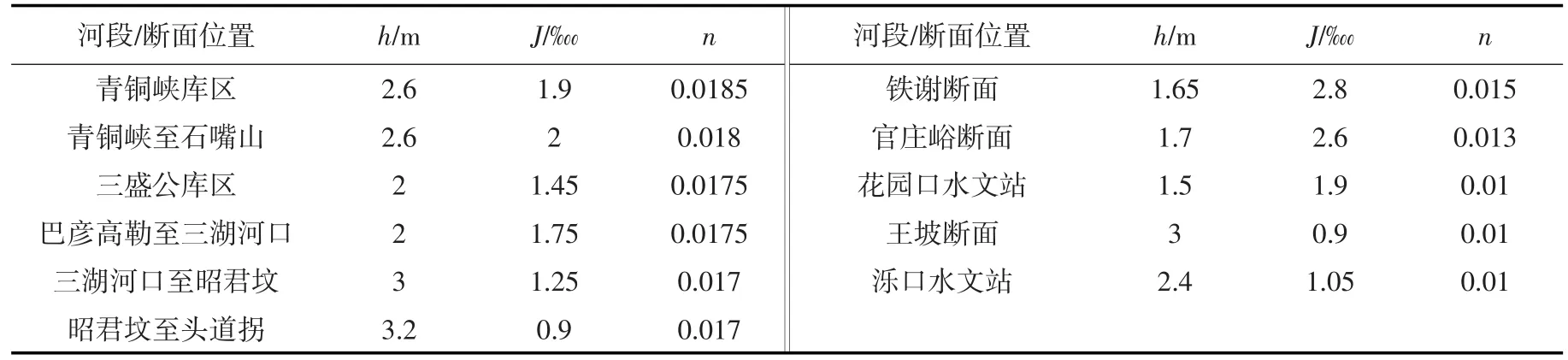
表2 黄河实测资料水力因子

此外，利用长江沙质河段大量实测资料对本文计算方法也进行了验证见图5，所取验证资料的水力因子见表3。

本文建立的推移质级配计算方法在检验时没有采取经验假定，但从上述检验图中看出，理论计算曲线同实测资料比较接近，计算得到的推移质泥沙中值粒径D50与各断面所取资料的平均推移质中值粒径基本相等。

4 结论

图2 式（13）与黄河上游实测资料的计算比较

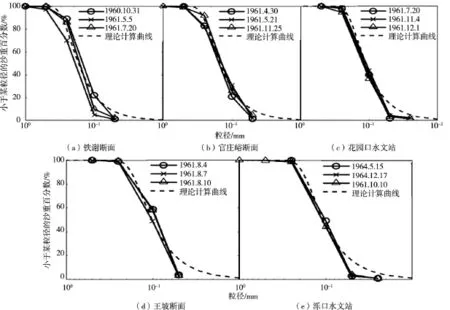
图3 式（13）与黄河中游与下游实测资料的计算比较

表3 长江实测资料水力因子

图4 式（13）与长江实测资料的计算比较

本文在总结前人研究成果的基础上，从分析沙质河床近壁紊动源区的泥沙运动临界图景入手，运用垂向动量平衡原理，给出了沙质河床推移质沉浮的临界条件，即水流的垂向瞬时紊动流速等于2.7倍泥沙在水中的沉速。在此基础上列出垂向瞬时紊动流速的随机方程，并以垂向瞬时紊速具有高斯分布式为条件进行求解，并引入垂向紊动强度与近底粗糙度的计算式，建立了理论性强且又不需要已知特征粒径的推移质级配计算方法。

采用黄河、长江主要沙质河段大量推移质实测资料检验结果表明，本文从理论上建立的方法同天然河流实际颇为符合，可用于计算冲积河流沙质河段的推移质级配分布曲线，从而可便于提高沙质推移质输沙率计算的精度，对于冲积河流推移质泥沙的运动也具有重要的理论意义和实用价值，但对于紊动流速场与泥沙颗粒作用机理的理论探讨尚需进一步研究。

［1］窦国仁.论泥沙起动流速［J］.水利学报，1960（4）：46-62.

［2］张罗号.沙质河床推移质输沙率计算研究［J］.水利学报，2017，48（4）：467-472.

［3］李昌华.床面上泥沙绕流上举力系数的间接确定［J］.泥沙研究，1984（4）：60-63.

［4］张红武.冲积床面糙率模拟问题的探讨［J］.武汉水利电力学院学报，1986（3）：92-99.

［5］GESSLER J.The beginning of bedload movement of mixtures investigated as natural armoring in channels［R］.California：W.M.Keck Lab.of Hyd.and Water Res.，Cal.Inst.Tech.，1967.

［6］GESSLER J.Self-stabilizing tendencies of alluvial channels［J］.Journal of the Waterways Harbors&Coastal Engineering Division，1970，96（2）：235-249.

［7］董永华.非均匀推移质级配的实验研究［J］.人民长江，1989（6）：43-49.

［8］张启卫.推移质级配的计算方法［J］.泥沙研究，1990（4）：41-48.

［9］乐培九.非均匀沙推移质输沙率的研究［J］.水道港口，1991（1）：1-8.

［10］DIPLAS P，DANCEY C L，Celik A O，et al.The role of impulse on the initiation of particle movement under tur-bulent flow conditions［J］.Science，2008，322（5902）：717-720.

［11］张红武.粗顆粒推移质级配的理论计算［C］//水利水电工程靑年学术论文集.北京：中国科学技术出版社，1992.

［12］张绪进，赵世强，陈远信.非均匀推移质级配研究［J］.泥沙研究，1990（3）：48-55.

［13］陆永军，张华庆.非均匀沙推移质输沙率及其级配计算［J］.水动力学研究与进展，1991（4）：96-106.

［14］何文社，方铎，曹叔尤，等.平衡输沙条件下推移质级配［J］.自然科学进展，2002，12（10）：1113-1116.

［15］张瑞瑾，谢鉴衡，等.河流泥沙动力学［M］.北京：水利电力出版社.1998.

［16］张罗号.基于涡量-动量传递理论的天然河流流速与含沙量垂线分布公式［J］.水利学报，2014，45（4）：566-573.

［17］侯晖昌.河流动力学基本问题［M］.北京：科学出版社.1982.

［18］章梓雄，董曾南.黏性流体力学［M］.北京：清华大学出版社，2011.

［19］张罗号，张红武，张锦方，等.泥石流流速计算与模型设计方法［J］.人民黄河，2015，37（4）：18-24.

［20］张红武，江恩惠，等.黄河高含沙洪水模型的相似律［M］.郑州：河南科学技术出版社.1994.

［21］SHEVELEV F A.Investigation of the Basic Hydraulic Regularities of Turbulent Motion in Pipes［M］.Kiev：State Publishing House of Literature on Construction and Architecture，1953.（in Russian）

［22］张红武，李振山，方红卫，等.宁蒙黄河治理对策研究［R］.北京：清华大学，2016.

［23］张罗号.明渠水流阻力研究现状分析［J］.水利学报，2012，43（10）：1154-1162.

［24］安催花，鲁俊，吴海亮，等.黄河宁蒙河段分组泥沙起动（河道冲刷）特性研究［R］.郑州：黄河勘测规划设计有限公司，2016.