非对称ERCS离散混沌系统及其性能分析
池宜航 李奎 陈丹妮


摘要:该文构建了一种非对称椭圆反射腔(ERCS)离散混沌系统。首先建立了非对称ERCS系统的几何模型,并对系统的演化进程进行了详细描述。然后,对其产生的一维离散混沌序列的概率分布、李雅普诺夫指数等性能参数进行了计算分析。相比标准ERCS系统,该文构建的非对称ERCS系统从几何模型上不具备中心对称结构和上下对称结构,因此可从根本上克服标准ERCS系统中存在周期解的缺陷。
关键词:非对称,椭圆反射腔(ERCS),演化过程,概率分布,李雅普诺夫指数
中图分类号:TP309.7 文献标识码:A 文章编号:1009-3044(2018)31-0225-03
Performance Analysis of Asymmetric Elliptic Reflecting Cavity Discrete Chaotic System
CHI Yi-hang1,2,LI Kui1,2,CHEN Dan-ni3
(1. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China; 2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;3. 75839 Troops, Guangzhou 510000, China)
Abstract: In this work, a novel discrete chaotic system bearing the name of asymmetric elliptic reflecting cavity system(ERCS) is proposed. We first build geometric model of the asymmetric ERCS and describe the evolutionary process. Then, evolution process, probability distribution and Lyapunov exponent of the pseudo-random sequence produced by the system are calculated and analyzed. Compared with TD-ERCS for which the tangent-delay operation is dispensable, the asymmetric ERCS has similar performance, while provides a simple way to generate pseudo-random sequence.
Key words: asymmetric elliptic reflecting cavity(ERC); evolution process; probability distribution; Lyapnov exponent
1 引言
自混沌理论出现以来,它就成为信息加密、保密通信等领域的研究热点。在计算机信息加密领域,离散混沌系统得到了较多的应用,典型的有Logistic映射、tent映射等,但这些离散混沌系统存在有密钥空间小、序列相关性依赖系统参数等缺陷,仍无法满足信息加密的需求。国内学着盛利元等人提出了一种基于切延迟的椭圆反射腔(TD-ERCS)离散混沌系统[1-3],并对其进行了性能分析,发现其具有全域零相关性,即序列相关性不依赖于系统参数,并且密钥空间远大于传统离散混沌系统等优点,在图像加密等领域得到了较广泛的应用[4-8]。
TD-ERCS系统的几何模型为一归一化标准椭圆反射腔,通过射线在腔内的反射映射来产生伪随机序列。由于椭圆存在完美的中心对称性和双轴对称性,因此TD-ERCS系统中存在内秉的周期解,在某种程度上破坏了系统的伪随机性。本文基于这一构想,为从物理模型上打破椭圆反射腔的对称性,构建了一种非对称的ERCS系统,并对其演化过程、概率密度分布、序列相关性等性能进行了分析计算,发现其具有与TD-ERCS系统相近的性能,并能有效破环后者中存在的周期解。
2 非对称椭圆反射腔模型
2.1 物理模型
非对称椭圆反射腔的几何结构由两个归一化的标准半椭圆组成:
2.2 系统演化过程描述
对于标准ERCS離散系统,可用一组映射关系式来描述系统的演化过程。但对于非对称的ERCS,由于映射过程涉及[μ1]、[μ2]两个参数的非周期性切换,无法由统一的映射关系式来描述。现给出非对称ERCS系统的映射步骤:
(a)当射线零点位于区间[-1,1]内时,参数发生切换;
(b)射线零点位于区间[-1,1]之外时,参数保持不变。
3 实验结果与分析
3.1 系统演化轨迹与演化进程
图3为非对称ERCS系统在相同初始点、不同入射角时射线的演化轨迹和[x]值的演化进程。图中,椭圆参数均为[μ1=0.5],[μ2=0.8],初始点坐标均为(0.7, 0.3571),入射角度分别为[α1=π/6],[α2=π/5],[α3=π/4],射线演化轨迹取值500个,[x]演化进程取值5000个。显然,在三种不同初值情况下,系统演化出现伪随机性。
3.2 xi的概率密度分布
3.2.1 理论推导
3.2.2 仿真验证
为验证以上假设和推导过程的正确性,现对非对称ERCS系统产生的伪随机[xi]序列进行概率统计并与(16)式进行比较,概率密度测试实验结果如图5所示。实验中,系统初值为x0=0.7,y0=0.3571,α=π/6,迭代50000次,计数盒尺寸为0.001,将计数结果归一化后显示为图中蓝色曲线。图中红色曲线为(16)式概率密度的理论计算结果。从图中可以看出,实验结果与理论推导吻合度较高,证明了上述假设和推导的正确性。
3.3 李雅普诺夫指数
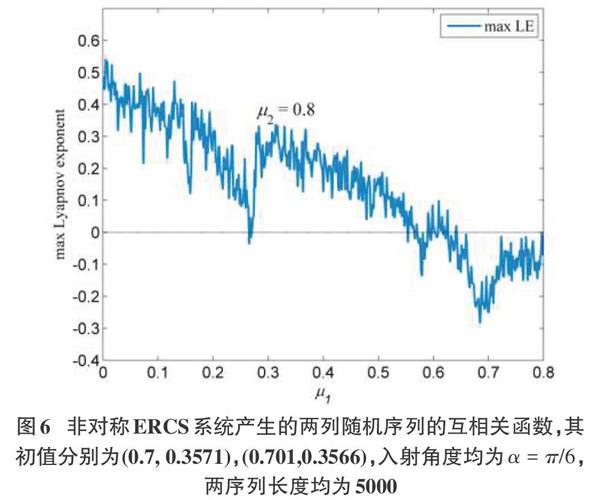
混沌系统的典型特性之一就是对初值的敏感性,对于两个相差很小的系统初始值,经过长时间演化后,所产生的序列具有零相关性。李雅普诺夫指数描述了系统中相邻两条演化轨迹在演化过程中的分离速率,它是系统处于混沌状态的充分条件。本小节利用Wolf算法计算了非对称ERCS系统的最大李雅普诺夫指数随系统参数的变化趋势,其中参数m2=0.8,m1取值范围为0.01~0.8,计算结果如图6所示。
从以上结果可以看出,当参数m2与m1差值较大时,系统的对称性弱,所产生的序列处于混沌状态,李雅普诺夫指数为正。随着m1逐渐增大靠近m2,系统对称性增强,所产生的序列逐渐表现出周期性,李雅普诺夫指数不断减小直到小于0,此时系统不再处于混沌状态,产生周期解。
4 结论
本文构建了一种非对称ERCS离散混沌系统,对系统的演化过程进行了数学描述和仿真计算,结果显示,仅具有一个对称轴的非对称ERCS系统不存在内秉周期解,克服了TD-ERCS系统中由于延迟参数选取不当会出现周期解的缺陷。对系统的状态变量的概率分布、李雅普诺夫指数等性能参数进行了计算分析,结果表明,本文所构6造的离散混沌系统具有与TD-ERCS相近的性能。
参考文献:
[1] 盛利元, 孙克辉, 李传兵. 基于切延迟的椭圆反射腔离散混沌系统及其性能研究[J]. 物理学报, 2004, 53(9):2871-2876.
[2] 盛利元, 曹莉凌, 孫克辉,等. 基于TD-ERCS混沌系统的伪随机数发生器及其统计特性分析[J]. 物理学报, 2005, 54(9):4031-4037.
[3] 孙克辉, 谈国强, 盛利元. TD-ERCS离散混沌伪随机序列的复杂性分析[J]. 物理学报, 2008, 57(6):3359-3366.
[4] 张坤, 甘小艇. TD-ERCS混沌系统和提升小波相结合的图像加密方法[J]. 激光与红外, 2013, 43:573-577.
[5] 贾伟尧, 潘宇, 简远鸣. 基于TD-ERCS混沌系统的图像加密方案[J]. 西南师范大学学报:自然科学版, 2012, 37:36-39.
[6] Zhang K, Fu X A. Color image encryption algorithm based on Tangent-Delay Ellipse Reflecting Cavity map System[C].Image Analysis and Signal Processing (IASP), 2012 International Conference on IEEE, 2012:1-4.
[7] Liao Q N. TD-RECS Chaotic System Based Digital Image Encryption Algorithm Protecting from Shearing Attack[C].Network Computing and Information Security, International Conference on IEEE, 2011:402-405.
[8] Yin L, Zhao J, Duan Y. Encryption Scheme for Remote Sensing Images Based on EZW and Chaos[C].Young Computer Scientists, International Conference for IEEE, 2008:1601-1605.
[9] Chen B. Improving autocorrelation and RFM autocorrelation performance of TD-ERCS sequence[C]//E-Business and E -Government (ICEE), 2011 International Conference on IEEE, 2011:1-4.

