基于地貌单位线的汇流模型在陈河流域的构建与应用

童冰星，李致家，温娅惠，孙明坤

(河海大学水文水资源学院，江苏南京210098)

0 引 言

陈河流域位于北温带，属大陆性季风气候区，多年平均降水量700～900 mm；河流水量主要系雨水补给，局部暴雨是发生洪水的主要原因。流域地处秦岭北麓，为秦岭褶皱带，上游大部分为高中山区，海拔高程700～3 500 m，山势雄伟，地形起伏大，大部分区域的坡度在25°以上。这些因素导致陈河流域洪水陡涨陡落[1-5]，同时给流域的防洪工作带来极大的挑战；而经常使用的线性水库、滞后演算、马斯京根法逐级汇流演算的方法难以对这种快速涨落的洪峰进行有效准确的模拟[6- 8]。

基于地貌扩散与水动力扩散的流域瞬时地貌单位线法是一种有一定物理基础的流域汇流随机模型[9-12]。它主要是在数字高程模型(DEM)的基础上，根据流域汇流过程与地貌因子间的关系描述流域汇流的过程[13]。它所需要的参数少且对输入条件响应快，因而本文在陈河流域上以该单位线为基础构建汇流模型，并着重对洪水的洪峰部分进行模拟演算。

1 基于地貌扩散与水动力扩散的流域瞬时地貌单位线的原理

2002年石朋等提出的基于地貌扩散与水动力扩散的流域瞬时地貌单位线[14]中指出：地貌扩散作用一般取决于流域的大小、形状等因素，主要反映流域中水系的疏密以及分布的形状等因素对于流域汇流的影响。它可以由Surka于1968年提出的宽度函数[15-16]来描述。宽度函数所描述的是距流域出口断面一定距离处的链数与距离之间的函数关系。其中的距离可以用拓扑长度来描述，也可以用几何长度来表示。水动力扩散作用一般与流域上的流速分布有关系，产生的根源在于流域上的汇流速度分布不均[17-18]，水动力扩散对汇流的影响可以用河道响应函数[19-21]来描述。基于宽度函数和河道响应函数可以得到流域瞬时地貌单位线。由于本文中的陈河流域处于高中山区，坡度陡峻(见图1)，河道中的洪水波一般属于运动波；因此，本文采用结合运动波理论的流域瞬时地貌单位线

(1)

式中，n为水系河源数；μi为水系中内链的平均长度；V为河道洪水波平均波速；t为时刻。

为求出1 h流域地貌单位线，应将式(1)积分，得到流域的S曲线，然后用S曲线计算得到流域1 h单位线

(2)

u(Δt)=S(t)-S(t-Δt)

(3)

式中，Δt为单位线时段长，此处取1 h。

图1 陈河流域坡度概率分布

2 陈河流域瞬时地貌单位线的提取

由式(2)可知，基于地貌扩散与水动力扩散的流域瞬时地貌单位线主要是由水系河源数、水系中内链的平均长度以及河道洪水波的平均波速这三个参数确定的。

2.1 水系河源数和水系中内链的平均长度的提取

水系河源数和水系中内链的平均长度均为流域水系的特征值，因此可以从流域DEM数据中提取。本文利用地理信息系统软件以90 m分辨率的DEM数据为基础提取流域的数字水系，并将提取出的水系与陈河流域1∶55万的Google地图影像进行对比(见图2)，确认两者相吻合后从数字水系中提取出陈河流域的河源数和水系中内链的平均长度(见表1)。

图2 提取的水系与Google地图对比

河源数目平均长度/m外链内链链水系总长度/m河道洪水波平均波速/m·s2133664311382725693127

2.2 流域河道洪水波平均波速的计算

对于流域河道洪水波平均波速v，本文对其进行率定。率定时采用陈河流域2003年到2012年之间的13场洪水资料，对每一场洪水均以0.1m/s为步长，将v从1 m/s到10 m/s之间连续取90个值逐次计算，并对计算得到的洪峰相对误差进行统计。

对计算结果进行统计分析，计算每取一个v值时洪峰相对误差均值Δi，以及取每一个v值时的洪峰相对误差平方均值Δj方。即

(4)

(5)

式中，j为v的值，以0.1为步长从1变化到10；i为每一场洪水的编号；n为洪水总的场数，取13。

由式(4)和式(5)计算得到洪峰相对误差均值随v变化曲线(图3)和洪峰相对误差平方均值随v值变化曲线(图4)。

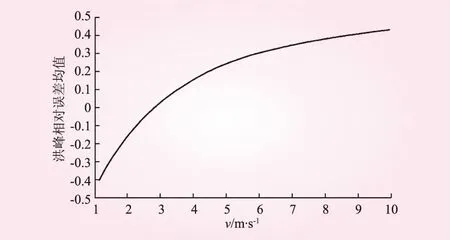
图3 洪峰相对误差均值随v变化

图4 洪峰相对误差平方均值随v变化

由图3可知：v从1 m/s变化到10 m/s时，计算的13场洪水的洪峰最初较低，相对于实测峰值整体偏小。随着v的增大，计算出的洪峰逐渐升高，并有部分洪水计算出的洪峰高于实测。且在v=2.7 m/s时计算得到的各场洪水的洪峰相对误差正负分布较为均匀，洪峰相对误差均值较小。随着v的进一步增大，计算出的洪峰普遍高于实测。结合图4可知：v从1 m/s变化到10 m/s时，洪峰相对误差平方均值首先随着v的增大而减小，在v=2.7 m/s左右时相对误差的平方均值最小，约为0.024。即各场洪水的洪峰误差分布最为集中，变幅最小。随着v的进一步增大洪峰相对误差平方均值迅速增大。

表3 模拟演算结果

综合上述分析，本文采用2.7 m/s作为陈河流域河道洪水波平均波速进行汇流计算较为合适。此时陈河流域瞬时地貌单位线的参数见表1。

采用表1中的参数值，结合式(2)及式(3)得到陈河流域瞬时地貌单位线u(1，t)(见图5)。

图5 陈河流域地貌单位线

3 基于地貌单位线汇流模型在陈河流域的应用

本文采用三层蒸散发模型(主要参数见表2)计

算流域产生的径流深，将其作为基于地貌单位线汇流模型(下简称“地貌单位线模型”)的输入，对陈河流域的13场洪水的洪峰部分进行模拟演算；并使用同样采用三层蒸散发模型进行产流计算的新安江模型，对陈河流域的13场洪水进行模拟演算，将两个模型计算得到的结果进行对比分析(见表3)。

表2 三层蒸散发模型主要参数值

由表3可知：新安江模型的平均洪峰相对误差为14.8%，地貌单位线模型的平均洪峰相对误差为7.6%；平均洪峰现时间误差为2.4 h，地貌单位线模型的平均峰现时间的误差为1.7 h。由此可看出，地貌单位线模型的平均洪峰相对误差和平均峰现时间的误差均优于新安江模型的计算结果。

基于表3分别对两个模型的洪峰相对误差的统计分析也表明，地貌单位线模型优于新安江模型计算结果。

综合上述分析认为，在陈河流域2003年到2012年之间的13场洪水中，以地貌单位线为基础的流域汇流模型取得了理想的计算效果。

4 结 论

本文采用90 m分辨率的DEM数据提取了陈河流域水系，同时以0.1 m/s为步长率定分析得到适合于该流域的河道平均汇流速度为2.7 m/s。进而以此为基础提取出陈河流域基于地貌扩散与水动力扩散的流域瞬时地貌单位线，构建了以地貌单位线为基础的流域汇流模型，并采用该模型与新安江模型对陈河流域上2003年到2012年间共13场洪水进行了流域汇流演算。计算结果的对比分析表明，在陈河流域上以地貌单位线为基础的流域汇流模型的取得了理想的计算效果。

然而，在将地貌单位线模型计算得到的洪水过程线与实测的流域出流过程线相比较时也发现：洪峰部分模拟的效果较好，但是涨洪与落洪部分常常过于快速，模拟效果并不是十分理想。这可能是由于将三层蒸散发计算出来的产流量全部作为单位线汇流演算的输入，没有针对不同的径流进行径流分割来分别作汇流演算，造成涨落的过程过快。因此，如何进行径流划分并分别对不同径流采用相适合的方法进行汇流演算，是需要进一步研究的问题。

[1] 芮孝芳. 水文学研究进展[M]. 南京： 河海大学出版社, 2007．

[2] 张恭肃, 黄守信, 贺伟程. 小流域单位线的非线性分析[J]. 水利学报, 1981(3)： 1- 9.

[3] 李致家, 姜婷婷, 黄鹏年, 等. 降雨和地形地貌对水文模型模拟结果的影响分析[J]. 水科学进展, 2015, 26(4)： 473- 480.

[4] 李巧玲, 王荣克, 董小涛, 等. 泾河上游植被覆盖动态及其与降雨径流的关系[J]. 水力发电, 2015, 41(11)： 21- 33．

[5] 姚成, 孙如飞, 李致家, 等. 下垫面变化条件下合河流域设计洪水修订[J]. 水力发电, 2015, 41(11)： 9- 13．

[6] 安东, 李致家, 阚光远, 等. 数据驱动模型与概念性模型的应用对比[J]. 水力发电, 2013, 39(12): 9- 12．

[7] 黄小祥, 姚成, 李致家, 等. 栅格新安江模型在天津于桥水库流域上游的应用[J]. 湖泊科学, 2016, 28(5)： 1134- 1140.

[8] 李致家, 包红军, 孔祥光, 等. 水文学与水力学相结合的南四湖洪水预报模型[J]. 湖泊科学, 2005, 17(4)： 299- 304.

[9] 陆桂华. 确定性方法推求地貌单位线[J]. 河海大学学报: 自然科学版, 1990, 18(6)： 80- 83.

[10] 芮孝芳. 由流路长度分布律和坡度分布律确定地貌单位线[J]. 水科学进展, 2003, 14(5)： 602- 606．

[11] 石朋, 芮孝芳. 由SSNs构建流域地貌瞬时单位线的研究[J]. 水科学进展, 2005, 16(6)： 799- 803.

[12] 芮孝芳. 地貌瞬时单位线理论的若干评论[J]. 水科学进展, 1991, 2(2)： 195- 200．

[13] 胡健伟, 陆桂华, 吴志勇. 基于地理信息系统技术的GIUH通用公式的应用[J]. 河海大学学报： 自然科学版, 2005, 33(3)： 269- 272.

[14] 芮孝芳, 石朋. 基于地貌扩散与水动力扩散的流域瞬时地貌单位线[J]. 水科学进展, 2002, 13(4)： 440- 444．

[15] SURKAN A J. Synthetic hydrographs: effects of network geometry[J]. Water Resources Research, 1968, 5(1): 112- 128．

[16] 包为民. 水文预报[M]. 北京： 中国水利水电出版社, 2009．

[17] 孔凡哲, 芮孝芳, 李燕. 基于空间分布流速场的单位线推求及应用[J]. 河海大学学报：自然科学版, 2006, 34(5)： 485- 488．

[18] 孔凡哲, 芮孝芳. 一种地形指数计算方法在Topmodel洪水模拟计算中的应用[J]. 水文, 2003, 23(3)： 16- 19.

[19] RINALDO A, MARANI A, RIGON R. Geomorphological dispersion[J]. Water Resources Research, 1991, 3(4): 512- 525．

[20] TROUTMAN B M, KARLINGER M R. Unit hydrograph approximations assuming linear flow through topologically random channel networks[J]. Water Resources Research, 1985, 21(5): 743- 754．

[21] RODRIGUEZ-ITURBE I, VALDES J B. The geomorphological structure of hydrologic response[J]. Water Resources Research, 1979, 15(6): 1409- 1420．