关于封闭式防渗墙顶部应力增量的估算

刘 娜，何文安

(1.长春工程学院土木工程学院，吉林长春130012；2.吉林省电力勘察设计院，吉林长春132001)

0 引 言

在深厚覆盖层上修建土石坝，心墙-防渗墙体系是常见的防渗形式之一。由于材料特性的不同，防渗墙的刚度较覆盖层要大许多，在上覆坝体自重作用下沉降必然不同，由于差异沉降的存在，在共同承担上覆坝体重量时，心墙和防渗体所承担的荷载并不是按一定比例分配的，而是在防渗墙顶部出现了应力集中现象。由于应力集中其顶部受力骤然增加，防渗墙顶部可能被压裂而出现裂缝，严重降低防渗墙的抗渗性能。目前，国内很多专家学者注意到这一点，开展了大量的研究工作。沈振中[1]针对心墙坝中心墙与坝基防渗墙合理的连接形式问题，结合某水库工程，采用非线性有限元法，分析研究了心墙基座与防渗墙不同连接形式下防渗墙的应力；邱祖林[2]采用三维非线性有限元，分析了某心墙坝工程软弱覆盖层上2道混凝土防渗墙(第1道为嵌岩式，第2道为悬挂式)的应力变形特性，并对其安全度评价方法进行了介绍；丁艳辉[3]以规划设计中的某高心墙堆石坝工程为例，进行了二维有限元应力变形分析，重点探讨地基混凝土防渗墙应力与变形的特点，研究结果表明覆盖层和防渗墙变形的不协调可导致两者之间发生复杂的相互作用；可使防渗墙体的局部发生较大的应力集中现象。综合分析文献[4- 6]可知，防渗墙刚度过大或者覆盖层的压缩量较大，两者之间就容易产生较大的不均匀沉降，从而导致防渗墙顶部所承担的荷载增加、应力增大，出现明显的应力集中现象。同时，心墙材料的强度越高，刚度越大，应力集中现象也越明显。但以上的研究主要是以工程为背景，利用数值计算的方法进行分析，缺少理论研究。

1 研究思路

针对在心墙-防渗墙坝型中封闭式防渗墙顶部出现的应力集中现象，本文试图从理论上提出一种由应力集中引起的防渗墙顶部应力增量的计算方法，为估算防渗墙顶部应力提供另一种途径。为了计算简便，本文首先做了假定；其次利用分层总和法近似估算出了防渗墙与两侧覆盖层的差异沉降Δs，在此基础上利用防渗墙的存在不会引起坝坡隆起的位移协调关系建立方程，推算出了防渗墙顶部由应力集中引起的应力增量；通过分析，说明该公式适合初步估算防渗墙顶部由于应力集中现象引起的应力增量，从而预估防渗墙顶部的应力状态。

2 计算公式推导与分析

2.1 基本假定

为计算方便作出如下假设：①防渗墙是刚性的；②坝体和坝基各材料均视为弹性且各向同性，并满足胡克定律。

2.2 计算差异沉降Δs

在沉降分析中，将整个坝体和坝基分为防渗墙宽度以内和防渗墙两侧两部分，如图1所示[7，8]。防渗墙宽度以内的沉降量包括3部分：防渗墙的压缩量、防渗墙顶至坝顶高度内坝体土体的压缩量和防渗墙底部沉降量。防渗墙视为刚体，压缩量忽略不计；防渗墙为封闭式防渗墙，嵌入基岩中，故防渗墙底部基岩沉降量可忽略不计；防渗墙顶部至坝顶土体的沉降量记为ΔH。防渗墙两侧的坝体和坝基产生的沉降量之和记为ΔH1，则防渗墙宽度以内的坝

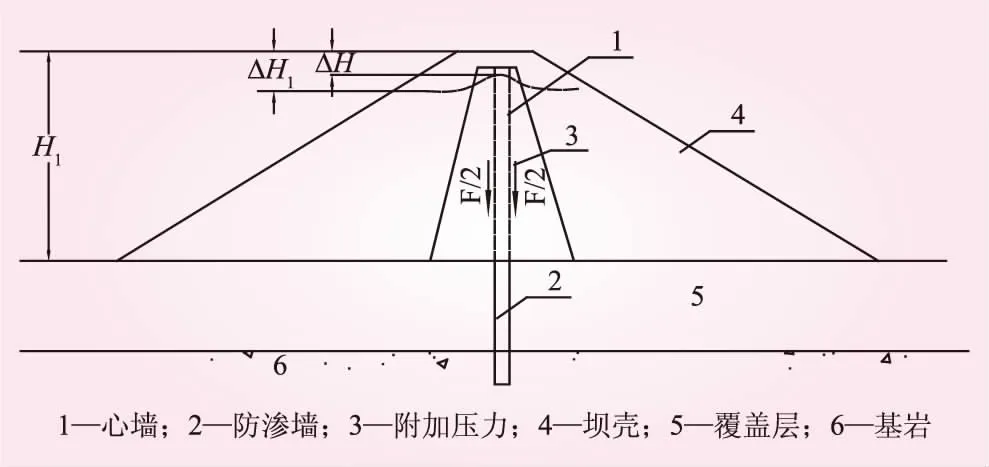
图1 坝体沉降分布示意

体和坝基与其两侧产生的差异沉降为Δs=ΔH1-ΔH。

由上述假定可知，坝体和坝基都视为弹性且各向同性并符合胡克定律，故ΔH、ΔH1都可以利用分层总和法计算，以ΔH为例进行说明。ΔH可表示为

(1)

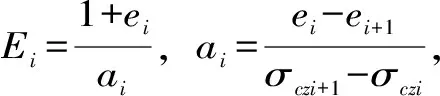
ΔH1值由坝体和坝基两部分沉降量组成，即

ΔH1=ΔHt+ΔHj

(2)

式中，ΔHt、ΔHj分别为坝体、坝基部分的沉降量。由此，便可以计算出差异沉降Δs。

2.3 计算应力增量q

若由Δs引起的防渗墙顶部应力集中的合力记为F，那么反过来防渗墙对心墙土体的应力集中合力也为F，将使心墙材料产生压缩，设其值为Δs′。由于防渗墙的存在并不会引起坝坡隆起，故必须满足Δs=Δs′。

若防渗墙伸入心墙深度d=0，将宽度为B的心墙上作用的应力集中合力F可看作条形荷载，荷载大小即为应力增量q=F/B。这时，心墙可看作作用着均布荷载大小为q的倒置条形基础，在应力增量q作用下心墙内任意一点处的垂直应力σz可利用地基中附加应力计算方法中的弗拉曼解答[9-10]得到，即

(3)

式中，q为条形荷载的强度；θ1、θ2分别为计算点和均布荷载边界点的连线和均布荷载边界(垂直线)的夹角，如图2所示。

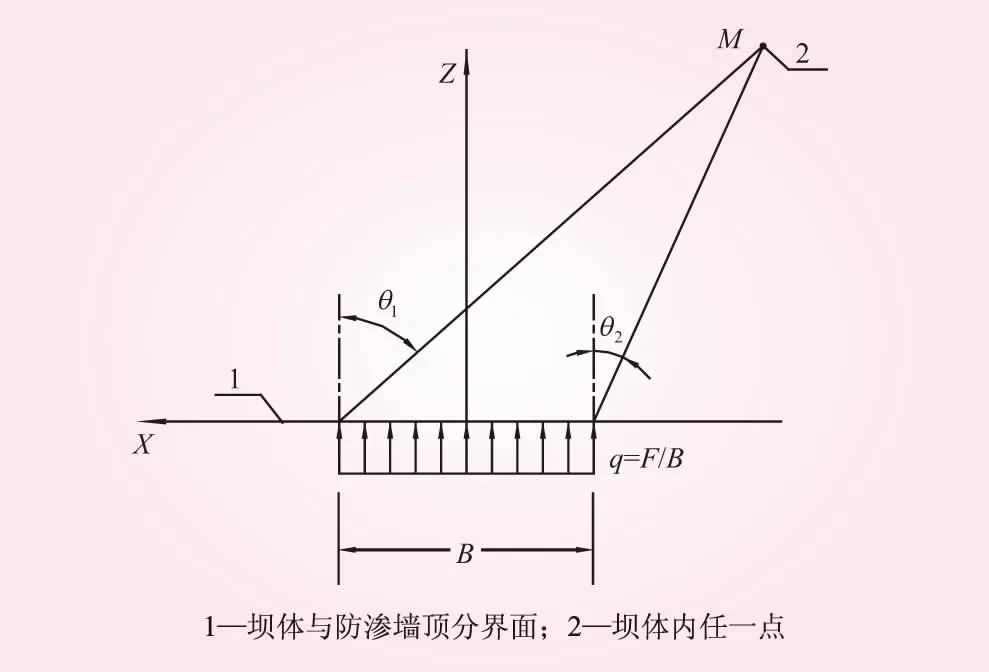
图2 条形荷载

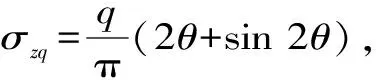
(4)

由式(4)变换，即求得由于差异沉降引起的防渗墙顶端的应力增量

(5)

2.4 分析

q=k·E0Δs

(6)

应力集中系数k中含有2个计算参数，防渗墙顶至坝顶高度H取值大小依赖于坝体的高度，据统计，目前土石坝高度可达到400 m，故H取值可取0～400；根据多年来的施工实践，防渗墙的厚度B不宜过大或过小，一般为0.6～1.2 m。因此，依据目前的实际工程情况，应力集中系数的取值范围在(0.03～0.09)，所以式(6)可表示为

q=(0.03～0.09)E0Δs

(7)

利用式(7)可以非常简便的求出防渗墙顶部由于应力集中引起的应力增量，同时可看出防渗墙顶部的应力集中现象主要取决于心墙材料的刚度和防渗墙与两侧覆盖层的差异沉降Δs。心墙材料刚度越大，防渗墙顶部的应力集中现象越明显，故在设计

时宜选择刚度相对较小的材料作为心墙材料，或者在心墙与防渗墙的连接处应进行特别处理。同时，防渗墙与两侧覆盖层的差异沉降Δs越大，应力集中现象也越明显。为了减小防渗墙与两侧覆盖层的差异沉降Δs，要考虑具体工程中覆盖层的特性和结合防渗墙的功能等综合因素选取合适的防渗墙的材料，或者在防渗墙两侧的覆盖层中进行灌浆，以提高地基的刚度，从而减小两者的差异沉降。

3 结 论

本文推导出一种防渗墙顶部应力增量的计算公式。利用该公式可初步估算防渗墙顶部的应力增量，从而进一步明确防渗墙顶部的应力状态。通过分析可得，心墙材料的刚度和防渗墙与两侧覆盖层的差异沉降对防渗墙顶部的应力集中有较大的影响。心墙材料刚度越大，防渗墙与两侧覆盖层的差异沉降越大，防渗墙顶部的应力集中现象越明显。

[1] 沈振中, 田振宇, 徐力群, 等. 深厚覆盖层上土石坝心墙与防渗墙连接型式研究[J]. 岩土工程学报, 2007,39(5)： 939- 945．

[2] 邱祖林, 陈杰. 深厚覆盖层上混凝土防渗墙的应力变形特征[J]. 水文地质工程地质, 2006(3)： 72- 76．

[3] 丁艳辉, 张其光, 张丙印. 高心墙堆石坝防渗墙应力变形特性有限元分析[J]. 水力发电学报, 2016, 32(3): 612- 167．

[4] 吕洪旭, 陈科文, 邓建辉. 瀑布沟大坝防渗墙应力分布特性及机理探讨[J]. 人民长江, 2011, 42(10)： 40- 44．

[5] 攀艳欣, 王瑞骏, 郭兰春. 深厚覆盖层地基土石围堰应力变形敏感性分析[J]. 水资源与水工程学报, 2015, 26(5)： 207- 211．

[6] 熊欢, 王清友, 高希章. 沙湾水电站一期围堰塑性混凝土防渗墙应力变形分析[J]. 水力发电学报, 2010, 29(2)： 198- 202．

[7] 郑秀培. 土石坝地基混凝土防渗墙设计与计算[M] . 北京: 水利电力出版社, 1979．

[8] 高钟璞. 大坝基础防渗墙[M]. 北京: 中国电力出版社, 2000．

[9] 杨进良. 土力学[M]. 北京： 中国水利水电出版社, 2009．

[10] 陈国兴, 樊良本. 土质学与土力学[M]. 北京: 中国水利水电出版社, 2002．

[11] 丁树云, 毕庆涛. 深厚覆盖层上沥青混凝土心墙土石坝的应力变形特征[J]. 水力发电, 2011, 37(4)： 43- 45．