矩形截面有限长螺线管磁场的计算
梁麦林 薛 凯
(天津大学理学院物理系,天津 300354)
在教科书和文献中[1-8],对螺线管的磁场有较多的讨论。对于无限长的密绕直螺线管,在忽略螺距影响的情况下,管内的磁场是均匀的而管外的磁场为零[1-3]。但是,对于有限长的螺线管,结论没有无限长螺线管那么简单[4-8]。当截面是圆形时,可以得到轴线上的精确磁场[2]。有限长的螺线管对称性不高,不能用安培环路定律计算,需要利用毕奥-萨伐尔定律,借助叠加原理进行计算,过程往往比较复杂。文献[4]中对于有限长螺线管的磁场进行了数值分析,不过没有给出一个明确的解析表达式。文献[5]讨论了螺线管内部磁场的求解方法,但没有涉及螺线管外部的磁场性质。在文献[6]中,给出了磁场的级数表达式,也许由于求和太过复杂,最后并没有一个简单函数的解析表达式。在文献[7]中,给出了磁场的积分表达式, 然后进行了数值分析。而在文献[8]中,借助矢势,先给出了磁场表达式的一个积分形式,然后进一步得到了磁场分布的级数表达式,最后讨论了某些特殊位置的磁场,包括中轴线上、管壁两侧靠近管壁处、远场区等。纵观这些研究,能够给出普通解析函数形式的依然是中心对称轴线上的磁场,其他位置的磁场都是积分形式或者级数形式。根据对称性质,如果螺线管的截面是圆形的,当知道非对称轴上一点的磁场时,其他位置的磁场也就应该知道了,这可能也是为什么圆形截面螺线管非对称轴上的磁场难以有一个简单解析表达式的原因。
对于非中心对称轴上的磁场,如果能够写成简单解析函数的形式,这样的结果还是很有意义的。一方面可以比较容易地分析和理解磁场的性质,另一方面也可以作为研究复杂问题的出发点。既然圆形截面时难以做到这一点,那么这里研究一种矩形截面的有限长螺线管,看看离开非中心对称轴上某些位置的磁场能不能写成简单解析函数的形式。当然要将所有地方的磁场都写成简单的解析函数形式是不现实的。经过计算发现,矩形截面有限长螺线管对称面上的磁场,确实可以用普通函数表示成解析形式,而不用写成积分形式或者级数形式。这里的普通函数解析表达式包括非中心对称轴上的磁场。
计算有限长螺线管磁场的方法如下:将螺线管的表面传导电流看成是某种介质的表面磁化电流,如果介质的磁化电流与螺线管的表面传导电流相等,那么介质磁化电流的磁场就与螺线管的磁场相同。而对于介质的磁化电流,磁场强度的环路积分是零,可以引入磁荷,这样就可以采取类似于处理静电场的方式处理静磁场(参看文献[2]中的389-401页)。接下来首先对磁荷方法计算磁场进行描述,然后具体计算有限长矩形截面螺线管的磁场,最后是总结。
1 用磁荷方法计算恒定电流的磁场
把传导电流看成是某种磁介质的磁化电流,就可以用磁荷方法计算磁场强度H。另一方面,让磁化电流等于相应的传导电流,进而可以确定磁化强度M,最后得到磁感应强度
B=μ0(H+M)
(1)
对于一个密绕螺线管,单位长度的匝数设为n,导线中的电流设为IC, 单位长度的面电流密度就是αC=nIC。考虑一个磁介质,其形状尺寸等与螺线管一样,磁介质内部没有磁化电流,磁化面电流密度就是αM=αC=nIC。这样磁介质的磁场就会与螺线管的磁场完全相同。
为了给出螺线管的磁场,我们假设磁介质是柱体,其轴线是z坐标轴,介质的磁化强度如下
(2)
式中,ez是轴线方向的单位矢量;Mi是介质内部的磁化强度;Me是介质外部的磁化强度。对于磁介质,这里没有传导电流,磁场强度H满足
(3)
式中
μ0M)·dS
(4)
就是磁荷。从式 (2)以及式(4)的定义我们知道,介质的内部没有磁荷,磁荷只分布在介质的两端。介质两端的磁荷面密度是
±σm=±μ0M=±μ0nIC
(5)
磁荷分布在介质两端的平行面上,这些磁荷决定了磁场强度H。螺线管的磁场强度类似于一个极化柱形电介质的电场。如果没有自由电荷,电场强度满足以下方程
(6)
式中
·dS
(7)
真空磁导率和磁荷(μ0,qm)与真空介电常量和束缚电荷(ε0,qp)互换, 磁场强度H就会与电场强度互换。因此,螺线管中磁场强度的计算相当于平行板电容器电场的计算。将式(2)代入式(1), 磁感应强度变成
(8)
螺线管内部的磁场有两部份,一部分是一个常数,另一部分是与磁场强度H有关的项,是由磁荷引起的磁场。螺线管外部的磁场完全由磁荷产生,体现在磁场强度H上。换句话说,磁荷产生螺线管外部的磁场和螺线管内部磁场的非均匀部分。
2 矩形截面螺线管的磁场
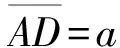

图1 螺线管的矩形截面
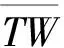
(9)
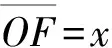
做如下的变量代换
φ
(12)
z分量的磁场强度式(10)变成
(13)
进一步利用积分公式
(atanhφ)+C
(14)
这里a是一个常数,C是积分常数,我们最后得到z分量的磁场强度
(15)
我们来分析一下这个结果: (1)靠近端点处,即-a 图2 函数U(z)的曲线,其中的参量是a=1.0,b=2.0 (a) x0=a/8; (b) x0=-a/2,-a/8,-a/32分别对应实线、短划线、长划线 从式(15)可以看出,因子U(z)的性质代表了磁场强度的性质。函数U(z)曲线如图2所示。图2(a)中,x0=a/8, 磁场强度先增加后减小。图2(b)中,x0=-a/2,-a/8,-a/32分别对应实线、短划线、长划线。参数x0=-a/2对应矩形截面的对称轴。图2(b) 表明,离开对称轴越远,磁场强度越小。 磁场强度的x分量是 (16) 在垂直于矩形截面的对称轴上,或者当x0=-a/2时, 磁场强度的x分量等于零即Hx=0。在极限z→∞的情况下,Hx∝1/z3,这要比磁场强度的z分量减小得快,从而在无限远处磁场强度只剩下z分量。参量x0和坐标z变化给出矩形截面对称面z-x上的磁场强度。 磁场强度式(15)、式(16)是在z=0处的带电矩形面的磁场强度。将z换成z±L/2会给出 矩形面在z=∓L/2处的磁场强度。考虑这样一种情况:在z=-L/2处有一个带正磁荷的矩形面,而在z=L/2处有一个带负磁荷的矩形面, 则该系统的总磁场强度分量是 对于放置在z=-L/2与z=L/2之间的有限长螺线管, 根据式(8),螺线管外的磁感应强度分量将是Bz=μ0Hz和Bx=μ0Hx,螺线管内部磁感应强度的非均匀分布部分也是同样的表达式。从前边对于式(15)和(16)的讨论,我们知道,当自变量z→∞,因子U(z)和W(z)都会趋于零。因此,当L→∞时,式(17)、式(18)中的磁场强度都会趋于零,也就是说螺线管外部的磁场和内部磁场的非均匀部分都会趋于零,这正是预期的结果。这里用普通的解析函数表达式得到了这样的结果。 图3中画出了磁场强度中的因子U(z+L/2)-U(z-L/2)≡G(z)随着坐标z变化的情况。螺线管处在z=-2到z=2之间。图3(a)表示的是螺线管外部的一条线上的磁场强度,而图3(b) 给出的是穿过螺线管内部的一条线上的磁场强度。在z=±2即螺线管的两端, 磁场强度改变方向。在z=0处即螺线管的中间部分,磁场强度要小于两端的大小。如果螺线管的长度是无限长,那么两端的磁荷在有限远处产生的磁场强度就是零,就像式(15,16)处分析的那样,磁场就变成无限长螺线管的磁场,磁感应强度在外部是零,内部是均匀的。 图3 磁场强度中的因子G(z)随着坐标z的变化情况相应的参数是a=1.5,b=1.0和(a)x0=a/8;(b)x0=-a/8。有限长螺线管处在z=-2到z=2之间,在z=±2即螺线管的两端, 磁场强度改变方向 计算了矩形截面有限长螺线管在对称面上的磁场,直接计算给出了简单的解析表达式,并对相关性质进行了分析。将螺线管的磁场看成是具有同样几何形状的磁化介质的磁场,发现有限长螺线管的磁场可以分为两部分的叠加, 一部分是常数部分,这部分只在螺线管的内部,另一部分是非均匀部分。随着螺线管的变长,非均匀部分不断减小,最终消失,只剩下螺线管内部的常数部分。由于矩形螺线管的磁场可以解析计算,将几个矩形螺线管叠加即可得到很多不很规则截面的螺线管,它们的磁场因而也是可以解析表达的。 [1] 张三慧. 大学基础物理学(下册)[M]. 北京:清华大学出版社,2007:82-83. [2] 赵凯华,陈熙谋.电磁学[M].3版.北京:高等教育出版社,2011:251-253. [3] 常同钦.截面为任意形状无限长螺线管的磁场[J].大学物理,2001(6):22-23. Chang Tongqin. Magnetic field of a infinite long solenoid with arbitrary cross section[J]. College Physics,2001(6): 22-23. (in Chinese) [4] 赵春旺,王克勋,刘前.有限长螺线管磁场的数值计算与分析[J].工科物理(现刊名为物理与工程),1997,4(2):14-17. Zhao Chunwang, Wang Kexun, Liu Qian. Numerical calculation and analysis of the magnetic field of a finite solenoid[J]. Engineering Physics, 1997, 4(2): 14-17. (in Chinese) [5] 王华军, 李宏福, 温越琼.螺线管中磁场的计算[J].四川轻化工学院学报, 1999, 12(4): 23-25. Wang Huajun, Li Hongfu, Wen Yueqiong. Calculation of the magnetic field in a solenoid[J]. Bulletin of Sichuan institute of light chemical engineering, 1999, 12(4): 23-25. (in Chinese) [6] 程昌林,王慧,李业凤.细导线密绕螺线管的磁场[J].物理与工程,2003,13(1):6-8. Cheng Changlin, Wang Hui, Li Yefeng. Magnetic field of a solenoid tightly wound with thin wire[J]. Physics and Engineering, 2003, 13(1): 6-8. (in Chinese) [7] 惠小强,陈文学.有限长通电螺线管空间的磁场分布[J].物理与工程,2004,14(2):22-23. Xi Xiaoqiang, Chen Wenxue. The magnetic field of finite solenoid with electric current[J]. Physics and Engineering, 2004, 14(2): 22-23. (in Chinese) [8] 丁健. 载流有限长密绕螺线管的磁场分布[J].大学物理,2009,28(8):28-30. Ding Jian. The magnetic field distribution of a current carrying tightly wound solenoid with finite length[J]. College Physics,2009, 28(8): 28-30. (in Chinese)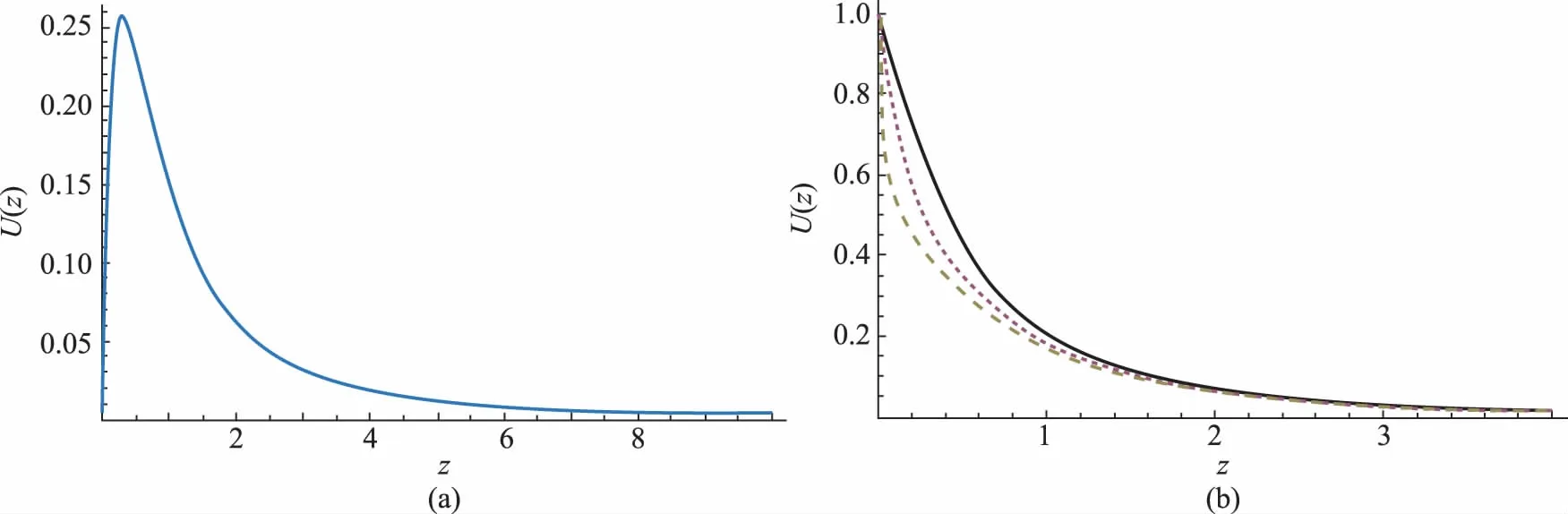

3 结语

