基于CATIA/CAA的复杂边界平面和曲面自动布点技术研究
韩志仁,王 刚,彩 辉,孟祥韬
(1.航空制造工艺数字化国防重点学科实验室,沈阳 110136;2.沈阳航空航天大学 航空宇航工程学部,沈阳 110136;3.中航工业沈阳飞机工业(集团)有限责任公司,沈阳 110850;4.中航沈飞民用飞机有限责任公司,沈阳 110034)
0 引言
随着航空制造业水平的飞速发展,对飞机零件的制造精度、装配精度的要求越来越高,精度低、耗时长的传统零件检验方法已经无法精确定量的描述零部件的实际几何状态,代替而来的是精确度更高的数字化测量技术。
数字化测量[1]有两种方式:一种是非接触测量,一种是接触式测量。前者应用最多的是三维激光扫描仪(3D Laser Scanner),通过激光扫描待测零件表面,可以生成点云数据,其数量级可达数十万,且必须对庞大的数据进行去噪处理才能使用,耗费时间较长,误差较大。相对于前者,后者应用最广泛的是三坐标测量机(Coordinate Measuring Machine)通过对零件上的点进行接触式测量,可以获取精确的数据,可以精确的进行误差检验。
目前国内用数字化测量设备检验零部件时,首先需要由工艺人员给出理论测量数据[2],具体包括建立测量坐标系、在数模上手动添加测量点、读取点的坐标值及矢量值并输出形成理论数据文件。在测量点较多的时候,测量数据的准备是一个简单但重复率高的工作,尤其是在面对飞机型号多、任务量大的情况下,将直接影响当前数字化检验的进度。为了缩短测量数据的准备时间,提高测量检验的效率,针对零部件的自动布点技术研究则显得尤为重要。
关于零部件布点的研究,国内学者只是研究了规则平面内自动布点的技术[3],该技术可以在零件侧面进行生成两排点,在腹板槽面选取三个点,对于自动布点难度大的复杂边界平面和曲面却没有提及,冀翠莲[4,5]等学者用质心Voronoi结构的采样方法,实现了曲面上测量点的自适应布,并进行了相关的仿真实验,但还没有在实际工程中进行应用,关于测量点自动布置已有很多方法,如何改良此类方法以至于能适用于现代制造业,并且CATIA作为数字化建模软件已经广泛地应用在国内的各行各业,特别是航空企业,因此针对这些问题,本文主要以工程应用为目的,基于CATIA的二次开发,研究了复杂边界平面以及规则曲面、自由曲面上的自动布点技术。
1 自动布点算法研究
1.1 自由曲面自动布点策略
自由曲面的定义是不能用数字表达式进行描述,对于待测曲面几何特征比较复杂的情况下,如何使用尽量少的测量点来精确描述曲面的几何特性就显得尤为重要。在测量点的数量尽可能少的条件下,如何确定测量点的分布,才能更加精确的描述曲面的几何特征。张美[6]使用质心Voronoi结构的自由曲面布点策略实现了测量点自适应分布,但在其采样过程中,需要不断计算曲面上点的高斯曲率值,进而导致效率不高,周保珍[7]使用二次测量法,完成了测量点的自适应分布,但其方法中的测点预测还局限在二维平面上,在满足测量精度的要求下,追求测量点的自适应分布是盲目的,因此根据这个问题,在满足精度的条件下,结合CATIA环境和工程实际,本文提出了“质心法”曲面布点策略。
“质心法”布点策略主要思想是,对于一个形状变化复杂的自由曲面,布点的目标是在整个曲面上均匀的生成点集,但是在CATIA中的环境中,要不断的对曲面曲率进行分析,计算机处理时间长,这样会降低测量的效率,因此本文采用在曲面质心处,分别选取UV两个方向,在这两个方向内做曲面上互相垂直的法平面,在空间均匀等间隔平移法平面,与曲面相交成线,两个方向的交线集在曲面上相交成点即为所求。其生成网格线的示意如图1所示,自由曲面布点策略的详细描述如下:
Step1:拾取目标曲面Q,获取质心C;
Step2:参考曲面Q和质心C,选取合适的两个方向U、V(例如可以在质心处建立坐标系,选取坐标系的某两个方向);
Step3:参考质心C和U方向,使用CATIA软件在空间中产生一个法平面F0,参考质心C和V方向在空间中产生一个法平面H0;
Step4:根据U、V方向,方向间距d1,d2平移该两个法平面F0、H0,生成法平面集Fi,Hj,i,j=1,2,3,4…;
Step5:法平面Fi与参考曲面Q相交产生交线Li,法平面Hj与参考曲面Q相交产生交线Lj;
Step6:交线Li与交线Li相交产生交点Pi;
Step7:Pi的处理,避免落到不可测或不可到达的区域。
为了使测量点分布均匀、合理,以及适应于实际情况,还考虑了以下四个方面:
1)U、V方向选取的具有代表性,方向的选取可以合理的进行布点的位置分布、可以解决实际中存在的复杂情况。
2)对于曲面上局部曲率大的区域,可以采用此方法进行局部细化,保证曲率大的区域内测量点足够的密度。
3)测量点的处理避免落入孔、洞等其他测量到达不了的区域。
4)可以运用此类方法进行多个方位的布点,点-点之间的间距可以控制,点与面边界、孔边界、障碍边界等之间的间距可控。可以选择选取还是不选取满足要求条件的点。
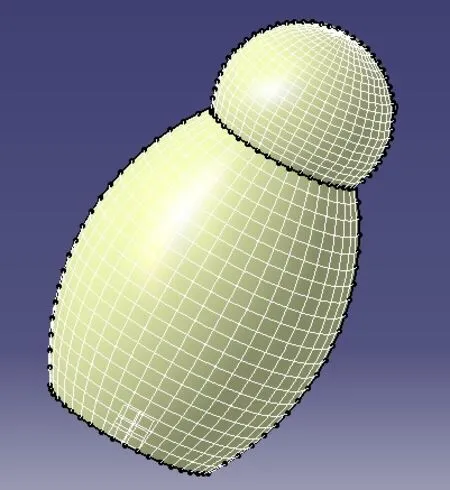
图1 平移产生网格线
1.2 规则曲面自动布点策略
规则曲面可以看成是由直线或曲线在空间按一定规律运动形成的。形成的曲面的动线称为母线,控制母线运动的线称为导线,如图2所示,产生曲面的母线导线分别为ABCN、NN1,曲面上测量点的密度通过生成曲面的导线和母线进行控制,因此规则曲面布点问题转化为曲线布点问题。针对曲线布点,应用最多的是等弧法,如图3(a)所示,就测量精确度而言,为了提高精确度,需要减小测量间距,这将导致测量工作量变大、效率变低,就制造角度而言,曲率大的部分,加工难度大,误差大,需要更多的数据点来检测,所以这种方法并没有考虑到曲面的复杂性,鉴于此,何改云[8]等学者提出了曲率方式布点法,如图3(b)所示,曲率大的地方,点的数量多,测量点过多时三坐标测量机在测量路径规划的时候更加困难。而曲率小的地方,测点数目过少以至于无法反映曲面的几何特征[8,9]。所以结合以上两种方法的优缺点,结合CATIA环境,本文提出了一种“曲率分区间布点”的策略。
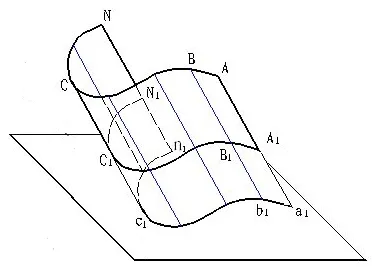
图2 曲面母线导线示意图
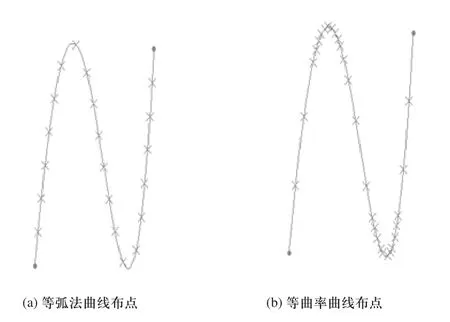
图3 曲线布点法
“曲率分区间布点法”策略主要思想是先把规则曲面布点转换为曲线布点,在曲线上先进行等弧长布点,在曲率大的区域再进行等曲率布点,使曲率小的地方测量点稀疏并能保证足够的测量点,曲率大的地方按等曲率规则增加测量点的数量,曲面上的点的分布随曲率变化,能批量生成能反映曲面特征的点。其策略详细描述如下:
Step1:选取目标曲面上的任一条母线l1、任一条导线l2;
Step2:在l1上采用等弧法布点(调用CATIA内部函数),输入间隔值d1,在l1上生成一系列均匀的点集pi,导线l2类似,i=1,2,3,4,…,n;
Step3:依次取出相邻的三个点pi,pi+1,pi+2,通过三点拟合出圆C,并求出半径r,则曲率k(x)=1/r,根据预设的曲率值界限为k,若k<=k(x),则不做处理,若k(x)<k≤1再进行等曲率预测下一个点(求出圆C与曲线l1的交点I1,如果I1的曲率满足区间则选取,不满足舍去,依次迭代pi+1,pi+2,…,pn,值得注意的是I1的曲率必须从和它相邻的两个点求得,如图4为母线或导线大曲率区间处理示意图),经过处理,在母线l1上的点集为g1{p1,p2,p3,…,pn},导线l2处理类似得到点集g2{p1,p2,p3,…,pn};
Step4:根据母线l1与点集为g1{p1,p2,p3,…,pn},在CATIA环境下,做法平面集fi,fi与目标曲面Q产生交线集Ii,导线l2处理类似得到交线集Vi;
Step5:交线集Ii与Vi,在CATIA环境下,使用相交命令,得到点集Gi;
Step6:点集Gi的处理。

图4 母线或导线大曲率区间处理示意图
1.3 复杂边界平面布点策略
在飞机存在一些复杂二维的零件,如尾翼,机翼纵墙,这些复杂边界平面如何布点才能最精确的反映其几何特征,一些学者如屈力刚[9]认为,三条相交的直线决定一个平面,即三个相交的直线产生三个交点,即不共线的三个点代表一个平面,三个点的几何特征可以代表整个平面的几何特征,这种方法没有提供点的分布,并且也只针对理想测量平面,在实际中合理的布点数目应该是4个[10],同时点的合理分布影响测量的质量,在实际零件加工过程中,如钣金件通过剪料、折弯、倒角等其他工艺加工之后,机加件在切削力、夹紧力、惯性力发生变化的时候,边界和顶点比其他区域更容易出现误差问题,这些地方的点能代表整个零件的几何特征和最大误差水平,结合厂里实际,为此本文提出了一种“顶点控制法”的布点策略。
顶点控制法的布点策略主要思想是在复杂边界平面上尽可能的获取到顶点附近的特征测量点。点的数量建议为4个,其简要示意图如图5所示,红色的点即为所求,其策略详细描述如下:
Step1:获取待测平面Q的轮廓(如在面xoy),获取其轮廓的几何中心m,获取轮廓各个顶点坐标Pi(x,y){i=1,2,3,4,…,n};
Step2:比较各个顶点的坐标,获取xmax、xmin、ymax、ymin;
Step3:分别以A(xmax,ymin)、B(xmax,ymax)、C(xmin,ymax)、D(xmin,ymin)顶点坐标建立一个包含此复杂平面的矩形ABCD;
Step4:连接几何中心m与这个平面Q的所有顶点,产生交线集I{I1,I2,I3,…,In};
Step5:设这个矩形ABCD的外接圆ρ2,内切圆的半径ρ1,连接矩形ABCD的对角线产生交点p以p为圆心,以为半径作圆Y(输入间距d,以为半径r,圆Y与产生交点集I{I1,I2,I3,…,In};
Step6:交点集I{I1,I2,I3,…,In}的处理。
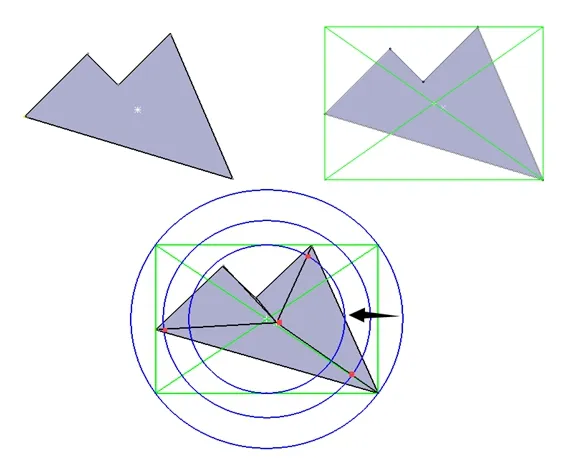
图5 复杂边界平面布点示意图
在复杂边界平面自动布点的过程中,还应该考虑以下四个方面:
1)如果该待测平面没有顶点,可以预先在该轮廓上手动做几个点;
2)测量点的处理避免落入孔、洞等其他测量到达不了的区域,区域外的点舍去;
3)三个点在一条直线上的舍去中间点;
4)当最后的总点数不足4个(落在目标区域外),可以选取几何中心m到顶点最远的几个顶点(如果某个顶点交线l已经存在测量点,则舍去这个顶点)作为测量特征点以至于总数达到4个。
2 功能实现
2.1 自由曲面自动布点功能
如图6所示为自由曲面自动布点方法简易流程图,在CATIA的环境里通过拾取元素待测曲面、拾取需要放置测量点集的几何图形集,即可完成功能的使用,关于此图中的交点处理,本文鉴于在厂里实际项目经验,对点到待测表面距离小于1/2网格距离的点集舍去,孔、洞边界处理类似,界面如图7所示,图8为软件使用界面及效果图,所以首先选取一个数据集用来放置生成的点,拾取曲面上的两个方向,输入这个曲面第一个方向、第二个方向的点与点之间的间隔值,点击“确定”既可以完成自由曲面上的布点。

图6 自由曲面布点方法简易流程

图7 点处理相关界面

图8 自由曲面布点软件使用界面和效果图
2.2 规则曲面自动布点功能
规则曲面布点方法的简易流程图如图9所示,图10为软件使用界面和效果图,先拾取目标区域的导线和母线(任意一条素线),拾取曲面,设置母线间隔值、导线间隔值,设置曲率临界点k,当k=0时,曲线以等弧法布点,当母线是直线,软件直接在直线上使用均匀布点方式,都满足要求,值得注意的是在有些曲面上,母线可以是导线,导线也可以是母线。
2.3 复杂边界平面自动布点功能
复杂边界平面布点方法的流程如图11所示,先选取目标平面,软件自动计算出包含该区域的外接圆半径R1和内切圆半径R2,用户根据这两个参数,合理设置间隔值,在软件后台,已经对点的选取做了处理,点击确定即可完成在复杂边界平面的布点,图12为软件使用界面和效果图。

图9 规则曲面布点流程图

图10 规则曲面布点软件使用界面和效果图

图11 复杂边界平面布点流程图

图12 复杂边界平面布点软件使用界面和效果图
3 应用实例
以某型号飞机的蒙皮曲面为例,将使用本软件的自由曲面自动布点模块,以及测量点输出模块。如图13首先选择一个几何图形集,拾取两个方向,拾取目标布点曲面,分别设置方向1、方向2的间隔值点击确定即可完成自动布点。图14为点的输出模块,可以批量输出点的坐标值和矢量值。
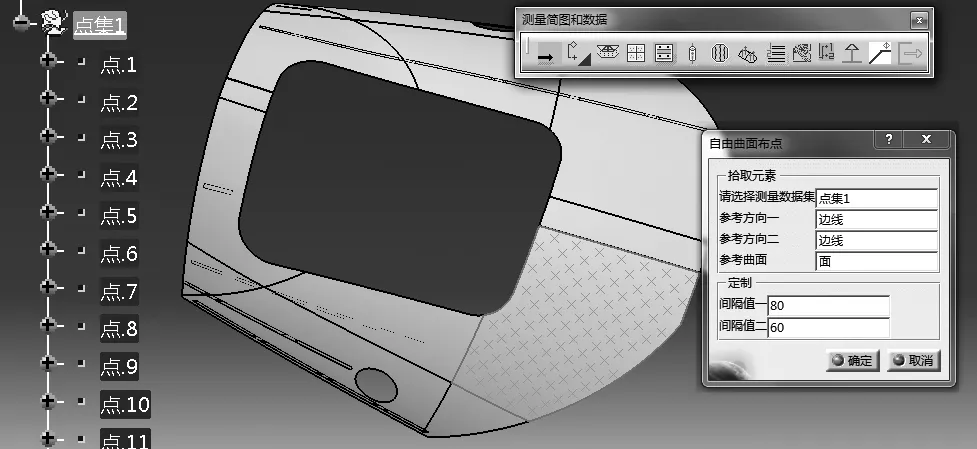
图13 蒙皮曲面上的布点
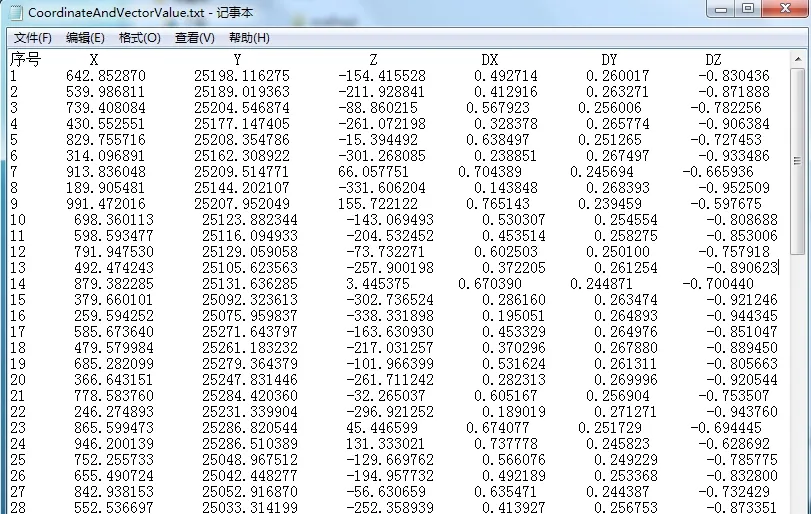
图14 点坐标值与矢量值的输出
4 结论
针对复杂边界平面布点、复杂曲面、规则曲面,本文提出了顶点控制法、质心法、曲率分区间布点法,结合厂里项目经验,在CATIA的环境下,基于以上方法开发的复杂边界平面和曲面自动布点的软件,能够快速的
【】【】生成一系列能代表目标区域几何特征的点,方便了测量业务人员将手工繁琐的工作实现自动化,同时能批量的输出点的坐标值和矢量值,提高了数据的规范性和精确性。在当前我国航空制造业快速发展、型号多、测量工作量大的情况下,缩短了测量数据准备的时间,很大程度上提高了飞机生产的效率。
[1]张少擎.基于MBD的数字化零件检测技术研究[J].航空制造技术,2014,(21):89-92.
[2]耿煦.基于MBD的三坐标测量检验技术研究[D].沈阳航空航天大学,2013.
[3]韩志仁,李子牮,彩辉.基于CATIA/CAA的快速布点技术研究[J].航空制造技术,2016,(09):62-65.
[4]冀翠莲.基于Voronoi结构的布点算法及其实施技术[D].山东大学,2005.
[5]刘佩佩.在机检测中空间曲面的形状误差评定及其测量不确定度估计[D].天津大学,2014.
[6]张美.自由曲面测量采样策略及轮廓度误差评定算法研究[D].天津大学,2013.
[7]周保珍.曲面测量方法研究及测量仿真[D].江南大学,2008.
[8]何改云,贾红洋.基于CAD模型的自由曲面自适应采样策略[J].电子测量与仪器学报,2012,(10):835-840.
[9]屈力刚,孙业翔,杨野光,叶柏超,田健琪.基于MBD的复杂特征检测工艺规划技术研究[J].航空制造技术,2016,(17):97-102.
[10]何章毅.智能化三坐标测量机软件关键技术研究[D].哈尔滨工业大学,2006.

