基于HFLANN的MSMA传感器动态模型参数识别
涂福泉,吕 杰,庄羽航,胡升谋,王云学
(武汉科技大学 机械自动化学院,武汉 430080)
磁控形状记忆合金MSMA是一种近年来出现的新型智能材料,其理论最大恢复应变可达6%左右,最大响应频率可达5000 Hz左右[1],具有在磁场驱动下形变率大、响应速度快、能量转换效率高、力能密度高及易控制等突出优点。MSMA与压电陶瓷、超磁致伸缩材料、形状记忆合金等智能材料类似,存在着迟滞现象,导致MSMA传感器输入与输出存在非线性、重复性差等缺点,严重影响了传感器的传感精度[2],并限制了MSMA材料及其传感器的应用。
为了解决迟滞问题,许多学者进行了相关研究,已提出 Preisach mode[3],Krasonse’skii-Pokrovskii(KP)hysteron[4],Prandtl-Ishlinskii(PI)[5]等迟滞模型。在这些模型中,Preisach是用一种概念简单的数学方法描述了迟滞现象的基本特征,因而得到最广泛地应用。然而,它不便于在线调整参数以适应运行环境的变化。文献[6]提出了一种线性参数化KP模型以及基于得出KP模型的逆模型,但推导精确逆模型的过程却很复杂;文献[7]提出了一种由一组基本的迟滞算子输出的叠加的Preisach模型,再通过神经网络确定这些算子的权重函数;文献[8]将迟滞算子用来拓宽神经网络的输入空间识别和控制压电陶瓷驱动器。该方法的成功表明了迟滞算子是一种解决迟滞问题有效途径。
近些年,人工神经网络已广泛应用于许多非线性和复杂系统的识别和控制,函数链接型人工神经网络[9]FLANN被用来识别非线性动态系统。由于多层感知器MLP网络一般用于识别和控制动态系统,而文献[10]将FLANN视为一种快速收敛和计算复杂度低的方法,一种单层人工神经网络,但可以有效地转换为多层感知器。FLANN的常使用扩展函数如正弦余弦或切比雪夫函数[11-12]来近似动态系统。鉴于此,这里提出了利用一种迟滞函数链接型人工神经网络HFLANN[13]用来识别MSMA传感器动态模型参数,并运用一种改进的粒子群优化算法PSO[14-15]来优化训练FLANN的参数。
1 HFLANN的组成
1.1 迟滞算子
近些年,人工神经网络已经广泛地应用于模型认知和系统识别中,但是人工神经网络只能近似一对一或者多对一的连续系统,而这种传统系统辨识技术很难直接用于辨识具有多值映射特征的迟滞非线性。为此,提出一种转换算子用来提取迟滞中的变化特征。经过迟滞算子变换后,可以将多值映射系统转化成人工神经网络可以辨识的一对一映射系统。
迟滞算子 h(x)[8]为

式中:x为当前输入;h(x)为当前输出;xp为位于 x之前最近的1个输入极值,称为主导极值;h(xp)为当输入为xp时的迟滞算子的输出。
特征如下:
引理 1当 x(t)∈C(R+),R+={t∣t≥0},C(R+)是R+上的连续函数。设输入信号x(t)是连续的,如果存在不同的时刻 t1和 t2(t1≠t2),x(t1)=x(t2),x(t1)和x(t2)属于一个上升曲线和下降曲线,从而得到hin(x)和 hde(x)是反对称的。再由 h(x)的单调性,即hin(x)和 hde(x)只有在极值点处相交,且 x(t1),x(t2)不是极值点,则 h[x(t1)]≠h[x(t2)]。
引理2如果存在不同的时刻 t1和 t2,设 t1>t2,h[x(t1)]-h[x(t2)]→0,则(t1)-x(t2)→0。
1.2 HFLANN的结构
在此,将函数链接型人工神经网络FLANN引入传感器动态特性的研究,函数链接型人工神经网络可被用于非线性动态系统。利用神经网络良好的逼近能力,建立传感器的动态数学模型,该方法所建模型阶次低、精度高,对数据个数和采样频率无特殊要求。在FLANN输入端使用线性无关的增强模式表达,使用单层网络就可以形成各种超平面函数,巧妙地构造网络结构,使其具有时延关系,能够建立出反映系统特性的动态模型[16]。
根据传感器动态校准时测得的输入、输出信号,建立差分方程形式的数学模型。利用函数展开型的函数链接,将传感器输入信号u(k),传感器输出响应y(k)以及两者的后向延时信号u(k-1),u(k-2),…,u(k-m),y(k-1),y(k-2),…,y(k-n)作为神经网络的输入信号,输入加权求和后,通过神经元功能函数产生输出信号。在这里神经元功能函数为简单一对一线性映射,经过功能函数映射后的输出信号ym(k)与传感器输出响应y(k)通过粒子群算法PSO对权值进行调整。多次训练得出的权值即为传感器数学模型的系数,并且可以根据不同的准确度要求建立不同阶次的模型[17]。其网络训练原理如图1所示,网络训练如式(2)所示:

建立3阶的动态模型,即选取m=3,n=3
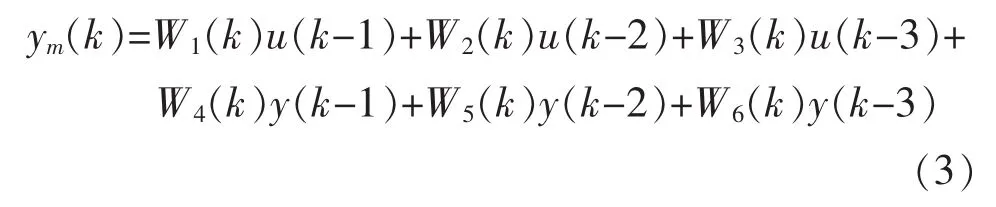
式中:u(k)为迟滞算子的输出;y(k)为过去输出;ym(k)为函数链接型人工神经网络的输出;W=[w1w2…wm+n]为加权因数向量。在此建立了3阶的动态模型,即选取 m=3,n=3。多次训练后,得到的 W1,W2,W3,W4,W5,W6即为传感器数学模型的系数。为了检验所建模型准确与否,给数学模型输入激励信号以得到响应,y(k)的初值(k=0,1,2)可设为零,也可用输入 u(k)(k=0,1,2)代替,得到模型输出 ym(k),然后进行参数优化训练。

图1 HFLANN结构Fig.1 Structure of HFLANN
2 改进的粒子群算法优化系统辨识
粒子群优化算法PSO[18]是一种简便有效的进化算法,现在被广泛地应用于各类优化问题,并且在传感器建模中也取得成功的应用[19-23]。它是将寻优的参数组合成群体,通过对环境的适应度来将群体中的个体向好的区域移动。基本PSO算法中的惯性权值和加速度因子全部为固定常数值。而良好的搜索策略,在初始阶段应该使惯性权值较大,有利于在全局范围内找到一个好的种群;在后期应使惯性权值较小,有利于找到一个精确的解。此外,加速度因子C:与粒子群全局最优值有关,它越大,说明粒子群的经验在算法中所占的比重越大。随着迭代次数的增加,应使C:逐渐增加,即增大粒子的群体经验,才能更好地体现群集智能的特点。这种改进的粒子群优化算法在文献[16]中被提出,在此将这种改进PSO算法用来训练FLANN人工神经网络的参数,图2为模型识别图。

图2 模型识别图Fig.2 Model identification diagram
惯性权重ω控制着以前的粒子速度对现在的影响。采取线性递减惯性权值的策略LDIW为

式中:tmax为最大允许迭代次数;t为当前的迭代次数;ωstart=0.95,ωend=0.4;c1,c2为正常数参数称之为加速因子或者学习因子,其控制着最大步长。加速度因子c1为固定值,c2为动态调整,即

PSO求解优化问题时,将解抽象为粒子,第i个粒子从n代进化到n+l代,r1,r2是独立的均匀分布的随机变量,范围是(0,1)。通过式(5)进行速度、位置更新,重复此过程直到达到用户定义的停止标准。即

式中:i=l,2, …,popsize;popsize 为粒子群包含粒子的个数;pid是第i个粒子的个体最好位置的第d维分量;pgd为群体中最好个体的最好位置的第d维分量。
辨识的主要目的是优化模型参数,传感器的模型输出 ym(k)如式(2)所示,对传感器模型的辨识就变成了一个对D(D=m+n)维参数,在此选取m=3,n=3,则 W1,W2,W3,W4,W5,W6的寻优过程,即使如式(7)所示的适应度函数为最小值。

式中:y(k)为传感器实际输出值;ym(k)为传感器模型的输出值;N为数据样本的数量。在此采用粒子群优化算法来训练模型参数。粒子群算法作为一种有效的方法用来优化训练有大量参数的函数。
3 MSMA传感器动态辨识结果
用粒子群算法优化模型参数的流程如图3所示,选取m=3,n=3,MSMA传感器输入信号采用振幅为1 N,频率为500 Hz的正弦激振力。粒子群优化算法在经过200次迭代后如图4所示,得到模型输出与实际输出如图5所示,图6显示了模型输出与实际输出的误差。识别和验证结果表明,最大误差低于5%左右,所以该模型可以很好的近似MSMA传感器动态。系统经过PSO优化训练得到的模型参数为wT=[-0.2442-0.1944 0.2275 0.6791 0.5176-0.1944]
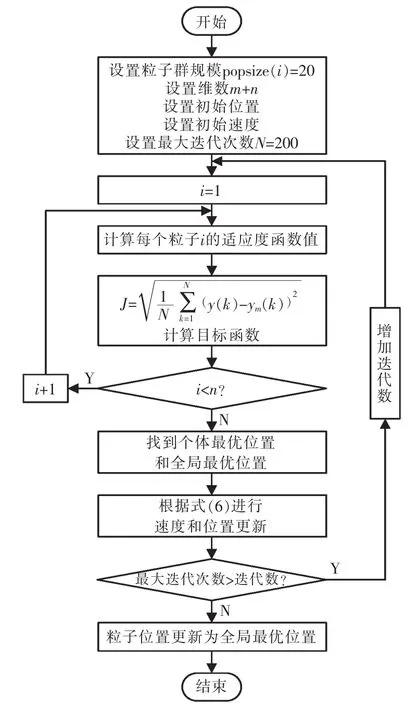
图3 用粒子群算法优化模型参数的流程Fig.3 Flow chart of optimizing model parameters using particle swarm optimization algorithm

图4 迭代曲线Fig.4 Iterative curve

图5 响应输出对比Fig.5 Response output comparison

图6 辨识误差Fig.6 Identification error
4 结语
将迟滞函数链接型人工神经网络应用于磁控形状记忆合金传感器动态模型参数识别。引入迟滞算子捕捉迟滞现象,FLANN人工神经网络来近似MSMA动态模型,利用改进后的粒子群优化算法PSO训练FLANN人工神经网络的参数。结果表明,利用函数链接型人工神经网络所建立的模型,能够精确地识别MSMA传感器动态模型参数。该算法具有较好的收敛性能,且计算复杂度低,从而提高了神经网络模型的精度。该模型为MSMA传感器的补偿器设计和控制提供了理论基础,为后续MSMA传感器的研究奠定了良好的基础。
[1]Suorsa I,Tellinen J,Ullakko K,et al.Voltage generation induced by mechanical straining in magnetic shape memory materials[J].Journal of Applied Physics,2004,95(12):8054-8058.
[2]Hwang Chih-Lyang,Jan Chau,Chen Ye-Hwa.Piezomechanics using intelligent variable-structure control[J].IEEE Transactions on Industrial Electronics,2001,48(1):47-59.
[3]Visone C,Davino D,Adly A A.Vector preisach modeling of magnetic shape memory materials oriented to power harvesting applications[J].IEEE Transactions on Magnetics,2010,46(6):1848-1851.
[4]Riccardi L,Naso D,Janocha H,et al.A precise positioning actuator based on feedback-controlled magnetic shape memory alloys[J].Mechatronics,2012,22(5):568-576.
[5]Su C Y,Wang Q,Chen X,et al.Adaptive variable structure control of a class of nonlinear systems with unknown Prandtl-Ishlinskii hysteresis[J].IEEE Transactions on Automatic Control,2005,50(12):2069-2074.
[6]Webb G V,Lagoudas D C,Kurdila A J.Hysteresis modeling of SMA actuators for control applications[J].Journal of Intelligent Material Systems&Structures,1998,9(6):432-448.
[7]Adly A A,Abd-El-Hafiz S K.Using neural networks in the identification of Preisach-type hysteresis models[J].IEEE Transactions on Magnetics,1998,34(3):629-635.
[8]Zhao X,Tan Y.Modeling hysteresis and its inverse model using neural networks based on expanded input space method[J].IEEE Transactionson ControlSystemsTechnology,2008,16(3):484-490.
[9]Huang J,Yuan H,Cui Y,et al.Nonintrusive pressure measurement with capacitance method based on FLANN[J].IEEE Transactions on Instrumentation&Measurement,2010,59(11):2914-2920.
[10]Dehuri S,Cho S B.Evolutionarily optimized features in functional link neural network for classification[J].Expert Systems with Applications,2010,37(6):4379-4391.
[11]胡志恒,李春光,王炎滨,等.一种复值函数型连接神经网络[J].信号处理,2003,19(2):95-99.
[12]胡志恒,王炎滨,虞厥邦.切比雪夫函数型连接神经网络在信道均衡中的应用[J].信号处理,2003,9(4):287-290.
[13]Tai N T,Ahn K K.A hysteresis functional link artificial neural network for identification and model predictive control of SMA actuator[J].Journal of Process Control,2012,22(4):766-777.
[14]张媛媛,徐科军,许耀华.改进PSO算法结合FLANN在传感器动态建模中的应用[J].振动与冲击,2009,28(1):1-3.
[15]Dehuri S,Roy R,Cho S B,et al.An improved swarm optimized functional link artificial neural network(ISO-FLANN)for classification[J].Journal of Systems&Software,2012,85(6):1333-1345.
[16]殷铭,徐科军,戴先中.基于FLANN的传感器动态特性研究方法[J].东南大学学报:自然科学版,1999,29(4):103-108.
[17]徐科军,殷铭.基于FLANN的腕力传感器动态建模方法[J].仪器仪表学报,2000,21(1):92-94.
[18]Kennedy J,Eberhart R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neutral Networks,Perth,Australia,1995.1942-1948.
[19]林卫星,张惠娣,刘士荣,等.应用粒子群优化算法辨识Hammerstein 模型[J].仪器仪表学报,2006,27(1):75-79.
[20]俞阿龙.遗传算法结合FLNN实现加速度传感器动态特性补偿[J].计量学报,2005,26(4):347-350.
[21]俞阿龙.改进遗传算法结合FLANN在加速度传感器动态建模中的应用[J].振动与冲击,2006,25(2):67-69.
[22]钱新,钱春华.电容压力传感器的FLANN建模方法[J].仪器仪表学报,2003,24(2):148-151.
[23]吴德会,赵伟,黄松岭,等.传感器动态建模FLANN方法改进研究[J].仪器仪表学报,2009,30(2):362-367.

