基于“互联网+”与群集智能的电能计量设备运维作业优化研究
张思建 ,张 捷 ,方彦军
(1.广东电网有限责任公司电力科学研究院,广州 510080;2.武汉大学 自动化系,武汉 430072)
随着电能计量设备运维作业要求的不断提升,传统作业模式早已无法满足新的需求。电网企业难以实时监控运维作业过程,无法掌握运维进度,且传统的作业模式存在任务分配不科学、巡检路径规划不合理、电能计量设备难以准确定位等问题,影响日常运维效率。目前计量营销现场作业大多采用人工表单方式,存在作业信息更新不及时、作业内容录入易出错、表单电子化程度低等问题,影响企业运作和管理效率[1]。
随着“互联网+”的概念被提出,互联网与各个传统行业的合并能够创造巨大的经济与社会效益。电力行业是国民经济的支柱性产业,对其他行业以及整个国民经济的发展起着至关重要的作用,因此,“互联网+”在电力行业的应用显得尤为必要。随着网络化、信息化进程在电网企业日常管理工作中的不断深化,电能计量设备运维作业支持技术的要求也日益提升。具体地讲,要求在充分考虑时间、路程、能耗、效率等要素的前提下,通过建立运维作业路径优化模型,研究相应优化算法,进而科学分配运维作业任务,合理规划作业路径,可视化管理作业过程,降低设备运维成本,提高运维效率,实现电能计量设备运维作业的科学、高效管理和动态优化调整。
本文首先研究并建立电能计量设备运维作业优化数学模型;其次,将“互联网+”概念引入电能计量设备运维工作,建立基于“抢红包”机制的运维任务动态分配机制;再次,针对粒子群算法对多极值问题的“早熟”现象,提出一种基于觅食与躲避行为的改进粒子群算法,并通过标准测试函数验证其有效性;最后,基于本文所建立模型及所提算法,进行电能计量设备运维作业动态优化问题的求解。
1 电能计量设备运维作业
1.1 运维作业需求分析
电网企业每日需对一定数量且分布于城市不同位置的电能计量设备开展运维作业。为提高工作效率,要求运维作业的管理工作能够在综合考虑时间、路程、能耗的前提下,实现各作业人员巡检路径科学规划。具体地讲,电网企业对电能计量设备运维作业优化的具体需求主要包括以下几个方面:①要求所有作业人员每日从运维中心出发开展各自的运维作业,且完成作业列表中要求的全部任务后,返回运维中心;②将运维人员行走路径的路程长度、实时交通状况等要素纳入评价标准,综合考虑时间、路程、能耗最优,实现对运维作业路径的实时优化;③要求优化模型能够实时输出各运维人员的有序任务列表和行进路线,并以一定方式发送至对应作业人员的手机APP终端,以指导其作业过程。
1.2 运维作业优化模型
基于上述需求分析,若将所有作业人员行进路线对应的路程总和与实时路况信息转化为相应的适应度函数值,则电能计量设备运维作业优化问题能够被转化成为一个多旅行商问题MTSP(multi-travelling salesman problem)进行求解。
首先,对于每日M的运维任务点总数,采用离散编码的方式构建任务列表,如式(1)所示:
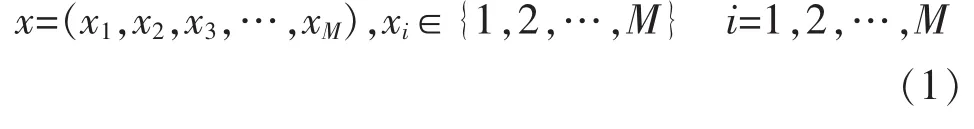
式中:xi表示任务点编号。由此可见,任务列表x为1~M的一个排列。对于出勤的N个作业人员,考虑到任务的均分,每个人员依次承担任务列表中M/N个任务点(不能整除时进行取整操作,此处不予讨论)。因此,各作业人员的任务列表依次从式(1)中截取对应部分,且长度均为M/N。考虑到统一从运维中心出发,且完成所有任务后须全员返回运维中心,各作业人员的实际行进路线如图1所示。其中,p为每个作业人员需要运维的任务量,即M/N。

图1 作业人员实际行进路线Fig.1 Real path of workers
在图1所示的各作业人员实际行进路线基础上,对各路径的路程与实时路况信息加权求和,作为该运维作业方案对应的适应度函数值。关于实时路况,可采用表1所示的系数予以体现,并作为权重值乘以对应路径的路程,得到的适应度函数值如式(2)所示。

表1 实时路况系数Tab.1 Real time road factor

式中:s0i1为第i个作业人员从运维中心至其第1个任务点的路程;ρ0i1为该路径对应的路况系数;s0ip为第i个作业人员从其最后一个任务点回到运维中心的路程;ρ0ip为该路径对应的路况系数;分别为第i个作业人员从其第j个任务点至第j+1个任务点的路程与路况系数。
1.3 基于“抢红包”机制的运维任务分配
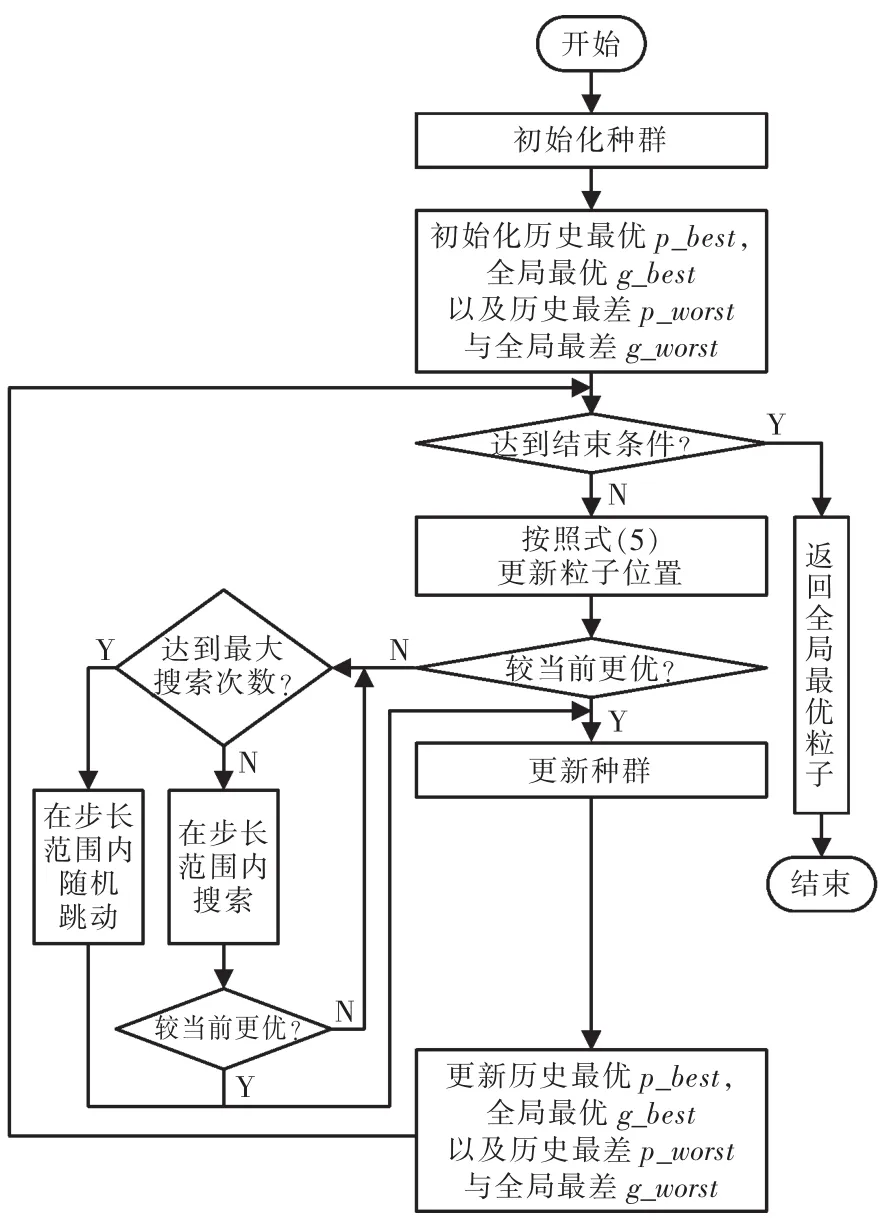
基于上述运维作业模型,在实际应用的APP中加入“抢红包”机制进行运维任务量的科学和自主分配。具体地讲,每日根据运维任务总量M首先进行一定基础任务量M0的科学预分配(M0 粒子群优化 PSO(particle swarm optimization)算法是由Kennedy和Eberhart于1995年提出的一种群体智能优化方法[2]。该算法基于对社会行为的模拟,每个粒子能够在解空间内根据自身的记忆以及从群体获取到的社会信息不断搜索。PSO算法在迭代初期往往收敛较快,但后期却容易陷入局部最优,出现“早熟”现象。粒子群算法的应用十分普遍,本文不再赘述,其公式表示为 式中:αl=c1r1;αg=c2r2;r1、r2~U(0,1);c1、c2为加速度因子;Vt和Xt为粒子在第t次迭代时的D维速度矢量和位置矢量;ω为惯性权重因子;为某粒子截止第t次迭代所经历过的最优位置矢量;为所有粒子在第t次迭代时的最优位置矢量。 种群中的粒子在初始化后按照上述公式进行迭代,当到达给定迭代次数或满足某个预设的寻优精度后,最后一次迭代产生粒子群的群体最优位置及其所对应的适应度函数值,即为粒子群算法所寻得的最优解。 经过多年的发展,PSO算法已具有一系列的改进策略,其性能也得到了不同程度的提升[3-6]。为进一步提升粒子群算法求解多局部极值问题时的算法性能,防止算法“早熟”现象,本文从增加粒子个体智能属性的角度出发,研究并提出了粒子的觅食与躲避行为模式,并提出基于觅食与躲避行为模式的粒子群优化算法PSOFA(PSO based on foraging and avoiding behavior)。 首先,为每个粒子引入觅食行为,即在按照迭代公式更新位置前首先进行判断,如果目标位置的适应度函数值较当前位置更优,则更新;反之,则开始粒子自身的觅食行为:在步长范围内随机搜索目标位置,若较当前位置更优,则更新,否则重新搜索;若达到最大搜索次数后还未找到更优位置,则在步长范围内随机跳动。觅食行为的目的在于增强粒子个体的全局搜索能力,防止多个粒子个体聚集在局部极值附近进而造成算法早熟。 其次,为粒子个体引入“躲避”行为模式。不同于标准PSO算法中所有粒子个体向全局最优及个体最优位置移动的迭代方式,“躲避”行为是在算法迭代过程中记录每一代的全局最差以及个体最差位置,并在速度更新公式中体现出粒子远离该最差位置的趋势。引入“躲避”行为模式的算法速度更新公式为 式中:αlw=c3r3;αgw=c4r4;r3、r4~U(0,1);c3、c4为躲避加速度因子;为某粒子截止第t次迭代所经历过的最差位置矢量;为所有粒子在第t次迭代时的最差位置矢量。 综上所述,PSOFA算法流程如图2所示。 图2 PSOFA算法流程Fig.2 Flow chart of the PSOFA algorithm 为验证PSOFA算法对复杂问题的求解能力,选取较常规测试函数具有更高复杂度[7]的经旋转变异的函数对算法性能进行测试。此外,选取标准粒子群算法PSO,带扩展记忆的粒子群算法PSOEM[8]以及粒子群优化鱼群算法PSO-FSA[9]作为对比实验。算法参数设置如表2所示,测试函数选取如表3所示。 表2 算法参数设置Tab.2 Parameters setting of the algorithms 表3 测试函数Tab.3 Benchmark fucntions 仿真环境为Matlab/R2007b,目标函数维数设为30维,种群规模50个,最大迭代次数5000代,各算法独立运行30次,各算法进化曲线如图3~图5所示。由仿真结果可见,对于变换后的高复杂度测试函数,标准PSO算法频繁陷入局部最优,已基本丧失其优化能力;改进后的PSOEM、PSO-FSA等算法在一定程度上能够保证其优化能力,但寻优精度有待提升;相比较而言,引入觅食及躲避行为的PSOFA算法既能够保证其全局优化能力,又能够保证较高的寻优精度,算法性能提升显著。 图3 Rotated Ackley函数优化结果Fig.3 Optimizing result of Rotated Ackley 图4 Rotated Griewank函数优化结果Fig.4 Optimizing result of Rotated Griewank 图5 Rotated Rastrigin函数优化结果Fig.5 Optimizing result of Rotated Rastrigin 由于PSOFA算法为连续数值运算,而电能计量设备运维作业优化模型采用1~M的离散编码,故上述模型与算法之间需要一个连续数值与离散数值互相之间的转换方式,即算法编解码方式。考虑采用对连续的PSOFA算法粒子个体各维度值进行大小排序,进而将各维度的具体数值转换为相应的大小序号,则每一个粒子个体可以转换为1~M的一个排列。具体地讲,算法优化范围设为[0,1],在计算PSOFA算法中每一个粒子适应度函数值前,先对其各维度值按照从小到大的顺序进行排列,将每一维度的数值转化为相应的序号后,再采用式(2)计算其适应度函数值。 以12个运维任务点、3个作业人员为例,首先初始化运维中心至各任务点以及各任务点两两之间的路程与路况信息。以式(2)为目标函数,并采用PSOFA算法进行优化,种群规模设置为50,算法终止条件设置为目标函数的最大调用次数达到5×104次。运维中心及各任务点的坐标如表4所示,其中编号为0的任务点表示运维中心。运维中心与各任务点以及各任务点两两之间的路况信息随机初始化后固定。基于穷举法(所需运算次数为4.79×108次)与PSOFA算法的结果对比如表5所示。基于PSOFA优化后所确立的各运维人员实际行进路线如图6所示。 表4 运维中心及各任务点坐标Tab.4 Locations of the OMT-EM coordinate and points 表5 实验结果对比Tab.5 Comparison of numerical results 图6 基于PSOFA算法优化的运维人员行进路线Fig.6 Path of workers optimized by PSOFA algorithm 由实验结果可见,PSOFA算法能够精确地寻得运维作业路径优化问题的全局最优解,且所需运算次数显著低于穷举法,保证了良好的实时性,在电网企业日常运维管理工作中具有可实现性。 本文结合电网企业对于电能计量设备运维作业的日常管理需求,建立了基于智能算法的运维作业优化模型。在此基础上,针对粒子群算法在求解多局部极值问题时所存在的“早熟”现象,提出了一种基于觅食与躲避行为模式的PSOFA算法,并应用于电能计量设备运维作业优化问题的求解。仿真分析表明,PSOFA优化算法较PSO及其若干主流改进算法而言具有更高的优化性能,且采用本文所建立的数学模型及PSOFA优化算法,能够在考虑路程、交通等要素的前提下快速、准确地完成对电能计量设备运维作业的科学、高效优化。 [1]刘欣欣,梁旭常,刘攸坚.电能计量设备运维现场作业信息系统的研制[J].电测与仪表,2014,51(22):12-16. [2]Eberhart R C,Kennedy J.A new optimizer using particle swarm theory[C]//Proceedings of the 6th International Symposium on Micro-Machine and Human Science,Nagoya,1995. [3]周雅兰,王甲海,黄聪.求解排列问题的分布估计离散粒子群优化算法[J].电子学报,2014,42(3):561-571. [4]Zhang Z H,Zhang J,Li Y,et al.Orthogonal learning particle swarm optimization[J].2011,16(6):832-847. [5]Beheshti Z,Shamsuddin SMH,Hasan S.MPSO:Median-oriented particle swarm optimization[J].Applied Mathematics and Computation,2013,219(11):5817-5836. [6]Wang H,Wang W J,Wu Z J.Particle swarm optimization with adaptive mutation for multimodal optimization[J].Applied Mathematics and Computation,2013(221):296-305. [7]RupamKundu,Swagatam Das,et al.An improved particle swarm optimizer with difference mean based perturbation[J].Neurocomputing,2014(129):315-333. [8]段其昌,黄大伟,雷蕾,等.带扩展记忆的粒子群优化算法仿真分析[J].控制与决策,2011,26(7):1087-1090,1100. [9]段其昌,唐若笠,徐宏英,等.粒子群优化鱼群算法仿真分析[J].控制与决策,2013,28(9):1436-1440.2 改进的粒子群优化算法
2.1 基本粒子群优化算法

2.2 基于觅食与躲避行为的粒子群优化算法

2.3 算法仿真分析





3 基于PSOFA的电能计量设备运维作业优化
3.1 算法编解码
3.2 仿真实例



4 结语

