基于CMOS图像传感器的微透镜平移算法研究

武岩，高春，魏巍

（长春理工大学计算机科学技术学院，长春 130022）

0 引言

图像传感器是将光信号转换为电信号的装置。目前，应用最为广泛的图像传感器主要有互补金属氧化物半导体CMOS图像传感器和电荷耦合器件CCD图像传感器[1]。随着集成电路制造工艺技术的不断发展和集成电路设计水平的不断提高，基于CMOS集成电路工艺技术制造技术的CIS（CMOS Image Sensor），由于其自身具有集成度高、成本低、动态范围宽和功耗小等优势，在诸多领域中得到了广泛的应用，如手机、笔记本、汽车、摄像机、保安监控、眼膜识别、医疗航天、视觉玩具等社会生活和工业生产的各个方面，特别是在数码相机、照相手机中的图像传感器应用市场前景非常广阔，因此，对于CIS的研究与开发具有非常高的市场价值[2]。

近年来，CIS技术得到了极大的重视和长足的进步。然而，在CIS分辨率的不断提高，集成像素单元不断增加的同时，光线通过微透镜阵列入射到像素内部光电二极管位置上的光照强度持续减弱，特别是处在微透镜阵列边缘部分的像素，这种现象尤为明显。光照强度的不足进而引起整个CIS灵敏度和成像质量的下降。因此，必须通过平移微透镜来减缓这种现象[3]。针对微透镜的平移计算操作，研究人员提出了几种不同的平移算法，如相位差测试像素算法、平面坐标计算法以及拟合平移函数算法等。这些算法能够较好的计算出微透镜的平移量，但存在着计算微透镜平移量不准确，运算复杂度较高和计算量较大等的问题。

为了解决上述算法的弊端，更好的进行微透镜平移量的计算，本文针对CIS的结构，提出了一种可以减少微透镜平移计算量的算法，该算法在提高了微透镜平移量计算精度的同时，减少了计算平移量的时间。

1 CIS微透镜平移分析

当光线通过CIS上方镜头，照射到微透镜阵列上时，位于微透镜阵列中心位置的光线几乎是垂直照射到阵列像素中的光吸收区域[4]。而在微透镜阵列当中，由于光线经过镜头、微透镜和滤光片时产生折射作用[5]。因此，光线以倾斜的方式入射到像素单元，部分光线照射到像素内部的金属层上面，即不能照射到微透镜阵列像素中的光吸收区域，降低了入射到像素内部光吸收区域的光照强度，从而造成了CIS的成像质量变差[6]。

2 微透镜平移算法

微透镜平移算法的提出对于高分辨率CIS成像质量的提升作用尤为突出。目前已经提出了相位差测试像素算法、平面坐标计算法、拟合平移函数算法等微透镜平移算法，针对相关算法分析其优缺点和适用范围。

2.1 相位差检测像素算法

相位差检测像素算法是将一个2×2的像素阵列上的微透镜分别向不同的方向平移[7]，δ代表微透镜21a到微透镜21d的偏移量，D代表每个像素11a，11b,11c,11d在倾斜方向上的排列间隔，r0代表最大圆C0的半径，O11O31是微透镜21a中的光轴中心点O11与微透镜21c中的光轴中心点O31之间的距离，可以用勾股定理的表达式来表示。O31O41是微透镜21c的光轴中心O31与微透镜21d的光轴中心O41之间的距离。用线连接三个圆的中心点形成一个等边三角形，其中rmax代表微透镜 21a、21b、21c、21d 的最大的半径，距离 O11O31和距离O31O41是最大的半径rmax的两倍。

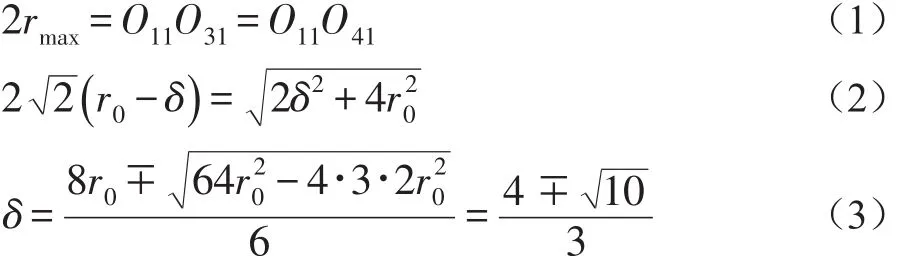
当δ＞r0的值时，微透镜 21a、21b、21c、21d 会覆盖其毗邻的像素11。因此，需要满足δ＜r0的值时，把它应用到等式（5）中，这是δ_max的值是r0的0.279倍。

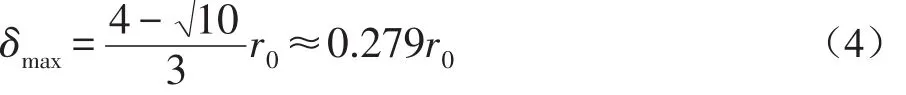
该算法提高了入射光进入每个像素的灵敏度，且不需要另外提供光瞳来形成微透镜，但是存在计算复杂且难于操作的问题。

2.2 平面坐标计算法

平面坐标算法是通过对微透镜阵列进行坐标化，取位于中心位置像素的中心点作为坐标原点，分别计算在X轴和Y轴方向的微透镜平移量，并通过计算出来的X轴和Y轴方向的微透镜平移量来计算处于该位置的微透镜平移量[8]。首先计算X轴和Y轴正轴方向像素的微透镜平移量，比如pixel（m，0）、pixel（k，0）、pixel（0，n）和pixel（0，1），假设pixel（0，1）的微透镜平移量为ΔS0,1，pixel（k，0）的微透镜平移量为ΔSk,0，则pixel（k，1）的微透镜平移量为ΔSk,1=sqrt（（ΔSk,0）2+（ΔS0,1）2），同理，可根据坐标来计算出其他任意位置的微透镜平移量。但该算法也存在一个缺点，即针对于计算主光线角度（CRA）照射下的微透镜平移量，而计算位于其他位置的微透镜平移量是通过它本身在X轴和Y轴投影的像素平移量的平方和去计算的，这本身就存在一个明显的误差，同时一般镜头的CRA特性为非线性变化，这种误差就更加的明显。

3 基于模块的微透镜平移算法

随着CIS的不断发展，CIS芯片集成度越来越高，CIS上的像素个数也不断增多，由原来的几十万像素发展到现在的几千万像素[9]。因此，为了提高CIS的成像质量而去逐一的计算每个微透镜平移量，显然不太现实。在该背景条件下，人们不得不寻找一种在保证平移精度的基础上，减缓微透镜平移计算量的方法。为了解决上述问题，提出了一种在保证平移精度的基础上减少微透镜平移计算量的算法，即基于模块的微透镜平移算法[10]。本文的算法流程图如图1所示。

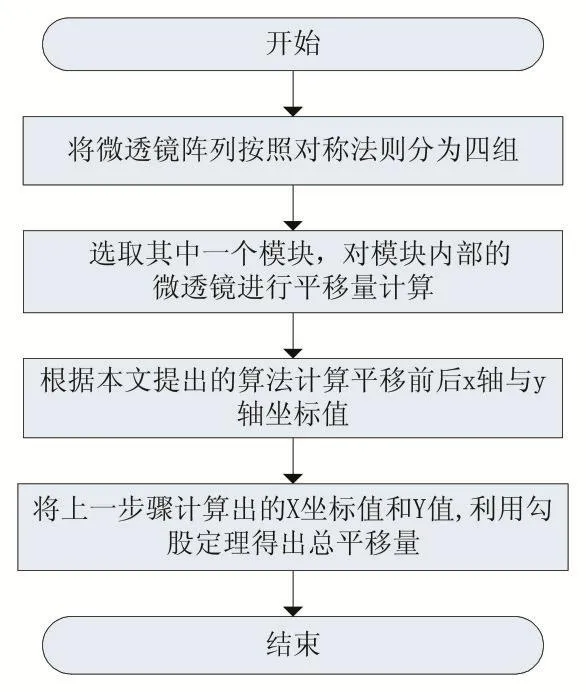
图1 本文提出的算法流程图

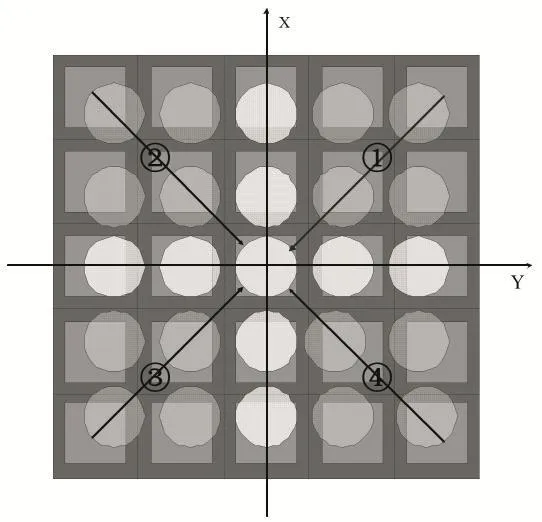
图2 微透镜阵列分块方法

基于模块的微透镜平移算法是依据CIS像素阵列是严格对称的特点，光线通过镜头照射到CIS像素阵列上，而镜头通常是圆形结构，在接受光照的情况下，形成的圆形光斑图案也依然是严格对称[11]。因此，提出了对微透镜阵列进行分块，再对单个微透镜进行平移量计算的算法。如图2所示，首先在微透镜阵列上建立坐标系，将微透镜阵列划分为四个模块。每个微透镜都按照黑色箭头的方向平移，当计算微透镜的平移量时，除坐标轴上的微透镜之外，计算其他微透镜的平移量时，只需计算这四个模块其中的一个模块，基于微透镜阵列相对于X轴和Y轴严格对称的法则，便可以得出其余三个模块的平移量。同理，坐标轴上微透镜平移量的计算方法同上。因此，该模块分组算法大大的减少了因逐个平移微透镜所带来的较大计算量，从而有效的提高了微透镜平移量的计算效率。该模块分组方法可由公式Block Size=INT（DeltaNpix/（2S））[12]计算得出微透镜阵列中的每个模块大小，其中Block Size代表模块的大小，即模块内行数或者列数的总和，Delta代表微透镜间距之间的改变量，Npix是像素排列当中行或者列的数目，S代表微透镜阵列边角的微透镜平移量，INT函数是为了保证整个微透镜模块进行平移。

该模块分组算法在可以确保精简计算量且提高光电二极管灵敏度的同时，不会增加额外的成本。在单个模块内部计算微透镜的平移量时，由于像素结构中像素之间的距离比与之对应的微透镜之间的距离要小。因此，本文采用基于像素间的最小串扰并提高像素中光吸收区域灵敏度的CIS微透镜平移算法。该算法涉及到几何光学中光线的折射原理等基础知识[13]，具体的计算方法如图5所示：

图3 计算微透镜平移量示意图

具体的计算方法如图3所示，规定物距在坐标原点左边为正，右边为负；坐标轴上方为正，下方为负。为了便于求出光线入射点的坐标，可把光线的方程表示为:

按此公式可求得光线的入射角I。接下来按照斯涅耳定理 sinI′=（n/n′）sinI和公式 U′=U+I+I′联立来作进一步的计算，公式 L′=r+r（sinI′/sinU′）可变换为 L′=z+（y/tanU′）。因此，对于空间光线经球面的光路计算，需要使用矢量形式的折射定律。设光线从镜头初射时的交点坐标为 A（x0，y0，z0），其方向余弦为 L（cosα，cosβ，cosγ），已知球面方程即为 F（x，y，z）=0，则联立光学方程和球面方程，得方程组：

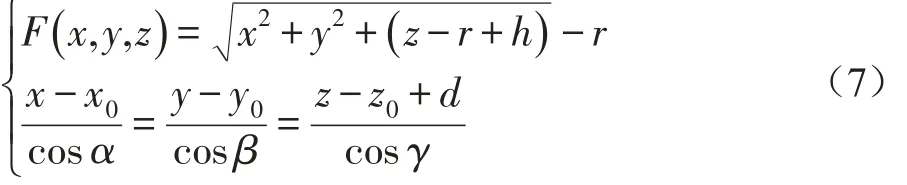
公式（7）中d为镜头到当前球面的距离，其中d=-L，r=sqrt（w2+（r-h）2）。利用相应的迭代法求以上方程组的解，即为光线与球面的交点 B（x，y，z）。过该点的法线方向单位矢量为：

公式（8）中，向量 M（λ，μ，ν）为法线的方向余弦。该法线的方向余弦与入射光线的单位矢量进行数量积，即可求得相应的入射角。

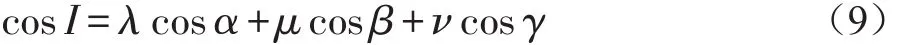
再利用折射定律求得折射角I′，即得P=N·A-N·A=n′cosI′-ncosI，其中 P 为待定系数，A′和 A 分别为折射光线矢量与入射光线矢量。然后利用折射定律的矢量形式：

将参数代入公式同样可求得折射光线的方向余弦。因此，只需将平移前微透镜的球心坐标（0,0,z）与平移后微透镜的球心坐标（x′,y′,z）进行比较，得出△x和△y，即为微透镜在X轴与Y轴方向上的微透镜平移量。设S为微透镜的总平移量，则利用数学公式勾股定理S=sqrt（（△x）2+（△y）2），即可得到微透镜的总平移量。

4 算法仿真验证与分析

在点光源光线主入射角为13.05度的照射下，使用LightTools光学建模仿真软件建立光学仿真的像素模型[14]。然后对微透镜分别使用文献[8]和本文所提算法进行平移仿真，采集微透镜的同样位置进行测试，测试的结果如图4和图5所示。由仿真结果可以看出，本文提出的算法可以更好地计算出微透镜的平移量，且使单个像素接收到更多的光照，从而提高了图像质量。

5 结语

微透镜平移算法的出现，解决了照射到微透镜阵列当中光吸收区域光线减少的问题。本文在对微透镜阵列进行模块划分的前提下，选取其中一个部分的模块进行微透镜平移，依据对称关系，其他模块的微透镜不需要额外计算就可以直接得出平移量，大大减少了微透镜平移的计算量。经过仿真验证，该算法可以在保证平移精度的情况下，可以有效地提高计算微透镜平移量计算效率。

图4 仿真结果

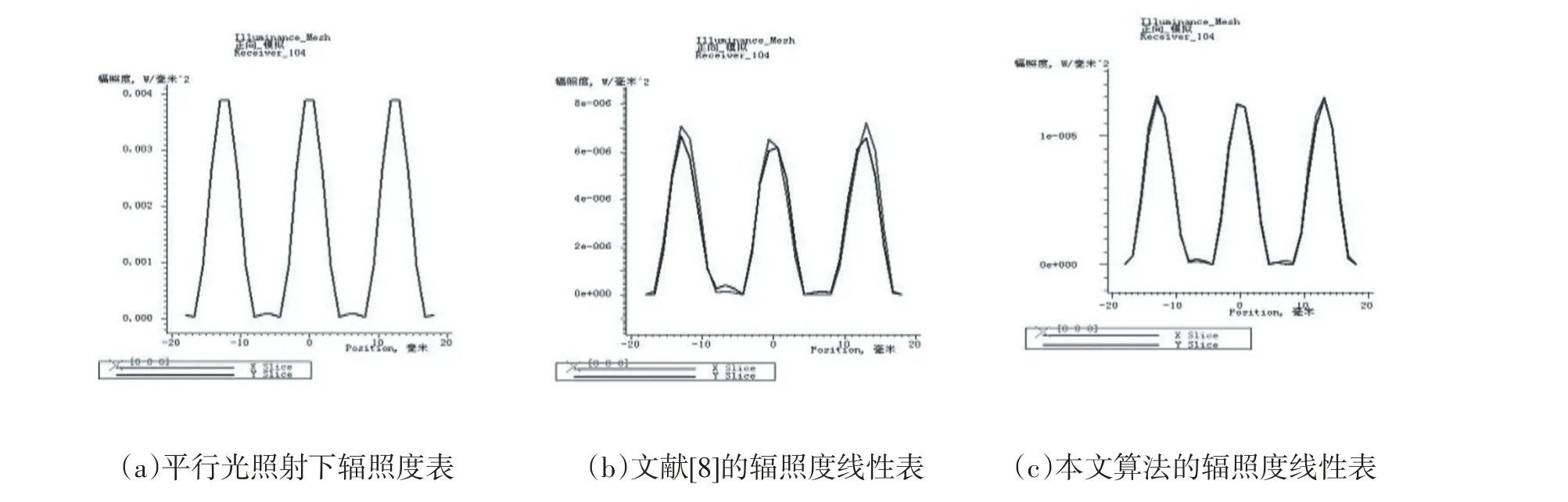
图5 辐照度线性表

[1]孙波,王晓艳.CCD图像传感器和CMOS图像传感器的比较研究[J].信息通信,2015(12):35-36.

[2]甘波,魏廷存,郑然.CMOS图像传感器芯片的自动白平衡算法[J].液晶与显示,2011.26(2):224-228.

[3]Feng C.Microlens Alignment Procedures in CMOS Image Sensor Design:US,US8068284[P]，2011.

[4]Tseng C X,Pang C P,Yang C L,et al.Design of Microlens on Pixel Array:US,US7687757[P]，2010.

[5]Campbell S P,Tsai R H,Agranov G A,et al.Alignment Among Elements in an Image Sensor:US,US7351945[P]，2008.

[6]Wakelin S,Derstine M W,Wong J S.Microlens Array with Spatially Varying Optical Property:US,US 6339506 B1[P]，2002.

[7]Okigawa M.Solid State Imaging Device with Microlens Shifted from the Center of the Photo Diode[J]，2015.

[8]Inoue T,Daiku H.Method for Calculating Shift Amount of Image Pickup Element and Image Pickup Element:US,US 20120262611 A1[P]，2012.

[9]Yoneda T,Inoue S,Kochi T,et al.Image Pickup Apparatus:US,EP 1667427 A1[P]，2006.

[10]郝劲波.基于微透镜阵列的三维物体识别[D].西北大学,2007.

[11]Agranov G A.Method for Calculating Circular Symmetrical Microlens/Color Filter Array Shift:US,US7796180[P]，2010.

[12]Solid State Image Sensors and Microlens Arrays:,EP1213764[P]，2009.

[13]王峥一,武伟璐,牛邦玉.微透镜及其阵列研究概况[J].科技与创新,2016(11):102-103.

[14]李赛.光场相机内微透镜阵列的误差分析及评价[D].哈尔滨工业大学,2016.