不同风场模式下“灿鸿”台风浪数值模拟及应用

陈鹏超，李瑞杰,2，李玉婷，勾 贺，戴 路

(1.河海大学 海岸灾害及防护教育部重点实验室， 南京 210098；2.河海大学 环境海洋实验室，南京 210098；3. 虚拟地理环境教育部重点实验室(南京师范大学)，南京 210023；4. 江苏省地理环境演化国家重点实验室培育建设点，南京 210023；5. 江苏省地理信息资源开发与利用协同创新中心，南京 210023；6.苏交科集团股份有限公司，南京 210000)

由于海岸线漫长，海域辽阔，我国平均每年有28次6m以上的海浪灾害发生，造成海滩事故七十余起。仅2015年北上型台风“灿鸿”就导致江浙沪三百多万人受灾，直接经济损失超85亿，其中江苏三十多万人受灾，直接经济损失达1.2亿。南通是江苏省重要的海滨城市，拥有海岸线210 km，其通州湾新区与宁波港将形成以上海港为核心的“一体两翼”发展格局，被誉为“长三角北翼经济中心”，处于濒江临海“T”字形经济交汇处，黄金水道和黄金海岸的交汇点，有利于建成综合性现代化国际深水海港，其近海资源丰富，具有独特的发展优势和不可估量的发展潜力，但南通沿海每年因台风浪给人民的生命财产造成巨大损失。

范从建，李瑞杰等[1]利用SWAN模型研究江苏滩涂围垦规划工程实施对其近海海域波浪场的影响，得出江苏北部沿海围垦规划区实施后波高变化不大，而其南部附近海域波高变化较大。戴路，李瑞杰等[2]对影响江苏近海的北上型台风“梅花”进行数值模拟，发现江苏沿海中北部海域波浪以涌浪为主，南部海域以风浪为主。梁连松，李瑞杰等[3]对舟山附近海域波浪场进行数值模拟研究，认为舟山群岛对台风浪的传播有较明显的阻挡作用。驱动风场对模拟结果的精度起着至关重要的作用，以上研究中并没有对不同的合成风场模型进行比选，而直接采用Holland梯度风场与背景风场合成作为海面的驱动风场，存在其不足之处。通过自嵌套模式对台风“灿鸿”进行模拟：选取SWAN (Simulating WAves Nearshore)海浪模型分别对3种不同的合成风场进行大范围海域数值模拟，通过卫星数据对比论证，选出最适合成风场模拟生成的波谱边界作为驱动来对小范围海域进行数值计算，最后再分别对近、远期区域建设用海规划实施后波高变化进行对比分析。

1 合成风场模型

在台风浪数值模拟中选取合理准确的驱动风场能更为有效地提高台风浪的计算精度。以ECMWF (European Centre for Medium-range Weather Forecasts)风场资料为背景风场，其数据空间分辨率取0.25°×0.25°、时间分辨率为6 h，并分别与3种不同的台风梯度风场模型进行叠加，构建新的合成风场作为SWAN模型的驱动条件。风场空间尺度为114°E～129°E、18°N～41°N，比模拟大范围海域稍大。

1.1 台风梯度风场模型

合理的选择台风梯度风场模型，正确的描述风场结构对海浪的计算至关重要[2-5]。选取3种常用的台风梯度风场模型：藤田模型、捷式模型和Holland模型，并与卫星数据进行比选。

目前研究人员大多根据梯度风原理先计算出台风气压场，再利用台风的气压场来计算台风梯度风场。3种模型气压场分布函数见表1，台风域内气压场模型为

P(r)=P0+(P∞-P0)F(r)

(1)

台风梯度风场模型函数由下式计算

(2)

式(1)求导代入式(2)可得出3种台风模型的梯度风速。式中P∞和P0分别为台风外围海面气压和台风中心气压，单位为百帕，台风中心气压资料来自中国台风网；r是计算点到台风中心的距离；B是Holland气压剖面参数，其确定存在一定的时空性差异，文中取B=1.5+(980-P0)/120；ρa为空气密度；f为科氏力参数。Rmax为最大风速半径，直接影响到风场的空间风速分布。在实测数据不足的条件下，常用经验公式来计算最大风速半径Rmax，取Graham，Nunn经验公式[6]

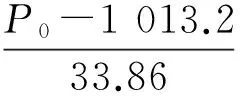
式中：φ表示中心维度；V为台风中心移动速度， km/h。

表1 3种气压场模型分布函数Tab.1 Three kinds of pressure field model′s distribution function

1.2 合成风场的构建

在台风中心附近，实际风场与背景风场存在较大偏差，需要新的合成风场进行校正。因此在台风中心附近采用背景风场与台风梯度风场模型以一定的权重系数叠加，构建新的合成风场

W(r)hc=EW(r)ERA+(1-E)W(r)t

(3)

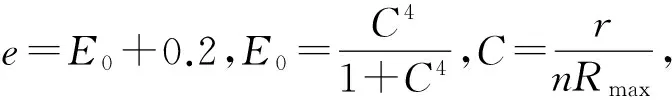
(4)

式(4)选取权重系数能有效保证外围背景风场和台风中心附近合成风场的平滑过渡。合成风场速度的计算分量为：u=-W(r)hc·cosθ；v=W(r)hc·sinθ。其中u为计算点到台风中心的速度沿东西方向上的分量，v为计算点到台风中心的速度沿南北方向上的分量，θ是计算点与台风中心的连线与正北方向的夹角。

2 模型设置

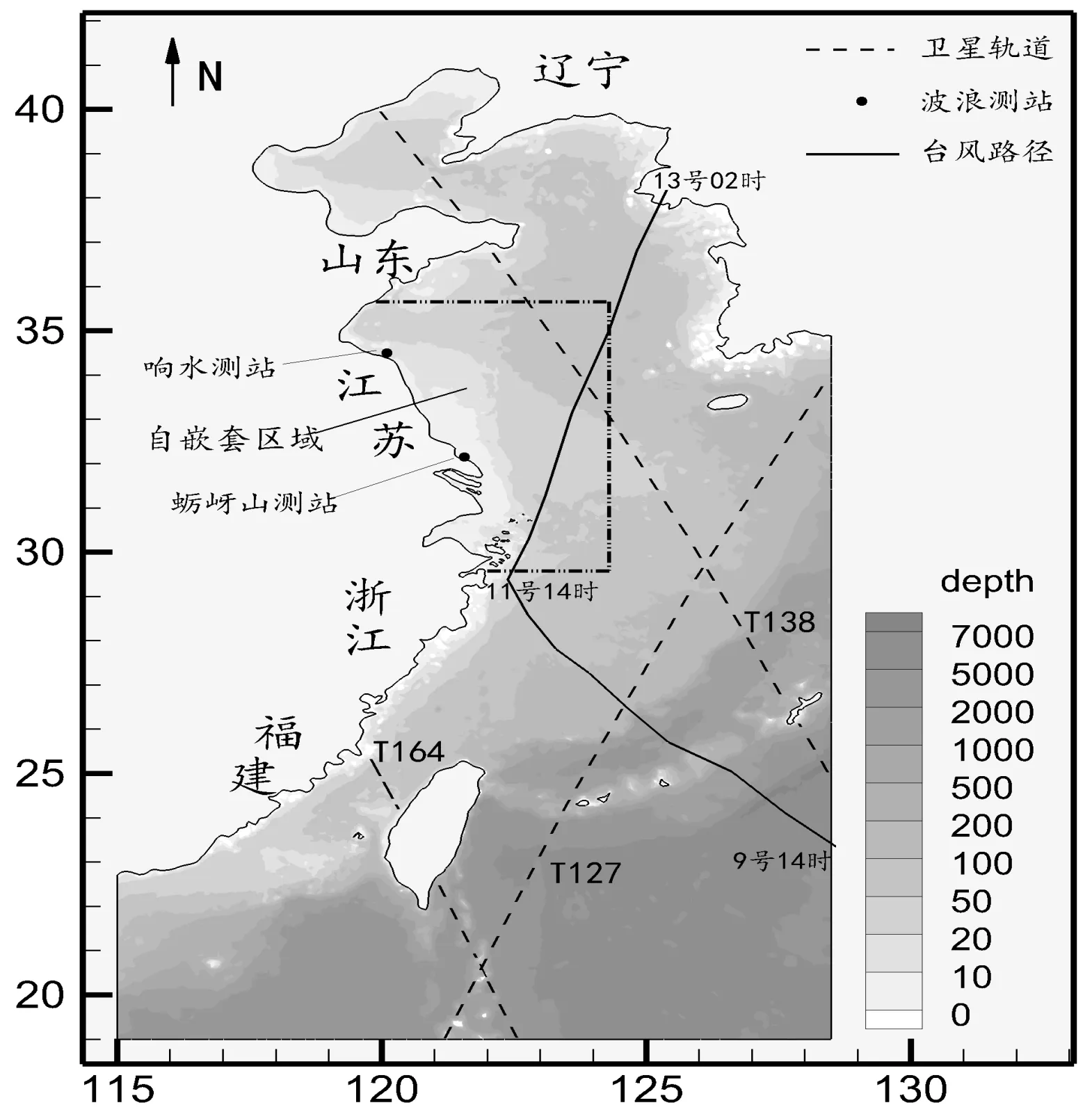
图1 模拟区域地形图Fig.1 Topographic map of simulated domain

利用SWAN海浪模式模拟“灿鸿”经过东中国海过程。为更加精确的模拟不规则岸线边界，模型采用非结构化三角网格[7]，其节点数35 742，三角网格数为69 956。计算范围为19°N～40.9°N，115°E～128.5°E。自嵌套为29.57°N～35.66°N，119.19°E～124.3°E，模拟区域水深地形图如图1所示。大范围为东中国海，其网格尺寸从近岸5 km到外海12 km逐步递增。自嵌套小范围工程附近海域进行网格加密处理约为0.4 km，向外海逐渐过渡到3.8 km。模拟时间为2015年7月4号8时～2015年7月13号2时，时间步长取15 min，迭代次数为10。为更好地研究近海工程对波浪场的影响，考虑绕射项[8]。

2015年9号台风“灿鸿”于6月30号20时在西北太平洋洋面上生成，7月3号升级为台风，7月11号16时40分在浙江舟山普陀朱家尖登陆，登录时中心附近最大风力达14级，风速45m/s，继续北上与7月13号凌晨在朝鲜西南部地区减弱为热带低压，随后对其停止编号。为验证台风浪的模拟效果，将波浪模拟值与已剔除无效数据后的Jason-2卫星轨道数据进行对比。在模拟时段内，Jason-2卫星主要有T127、T138及T164轨道经过东中国海。

3 模型优化

采用上述3种合成风场作为SWAN模型的驱动风场，模拟结果与卫星轨道数据进行对比。如图2所示。图2-a中3种合成风场模拟结果与T127卫星轨道数据对比效果基本一致，这是由于此时T127轨道所经过路径在合成风场叠加半径外部，模拟时采用同一背景风场ECMWF模拟所致。图2-b中发现在最大风速半径附近，藤田合成风场模型模拟值与卫星所测数据相差较大，不宜取。为定量分析3种方案的模拟效果，采用平均相对误差(MRE)、均方根误差(RMSE)、相关系数(R)和偏差(B)4个数学统计量对轨道T138和T164数据进行对比。

(6)

(7)

(8)

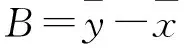
(9)

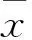
2-aT1272-bT1382-cT164图2 卫星数据和模拟有效波高对比Fig.2Comparisonofsatellitedatawithsimulatedsignificantwaveheight

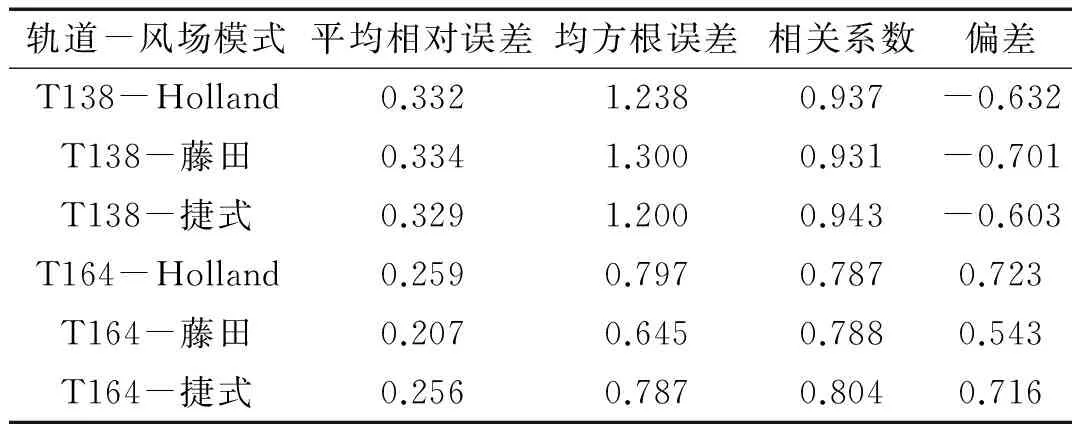
表2 不同合成风场模拟值与卫星数据统计对比Tab.2 Comparison of different synthesis wind field with satellite data

对比T138轨道统计数据发现其偏差为负值，即各合成风场模型的模拟波高值小于卫星数据。捷式较Holland合成风场，平均相对误差、均方根误差和偏差绝对值均有所降低，且相关系数增大；对T164进行分析，相对Holland合成风场，捷式合成风场的平均相对误差、均方根误差和偏差略有降低，且捷式合成风场的相关性更好。总体而言，可认为捷式与Holland合成风场模型较藤田模型可以更好地反映台风中心附近的风场，而捷式较Holland合成风场模拟效果更好。捷式合成风场特征时刻场图如图3所示，最大波高出现在台风中心右前方，与理论相符且风速与波高吻合度高，能够很好地模拟此次台风浪过程，以给小范围提供较准确的波谱边界条件。故选用捷式合成风场作为下文小范围自嵌套模型的驱动风场。

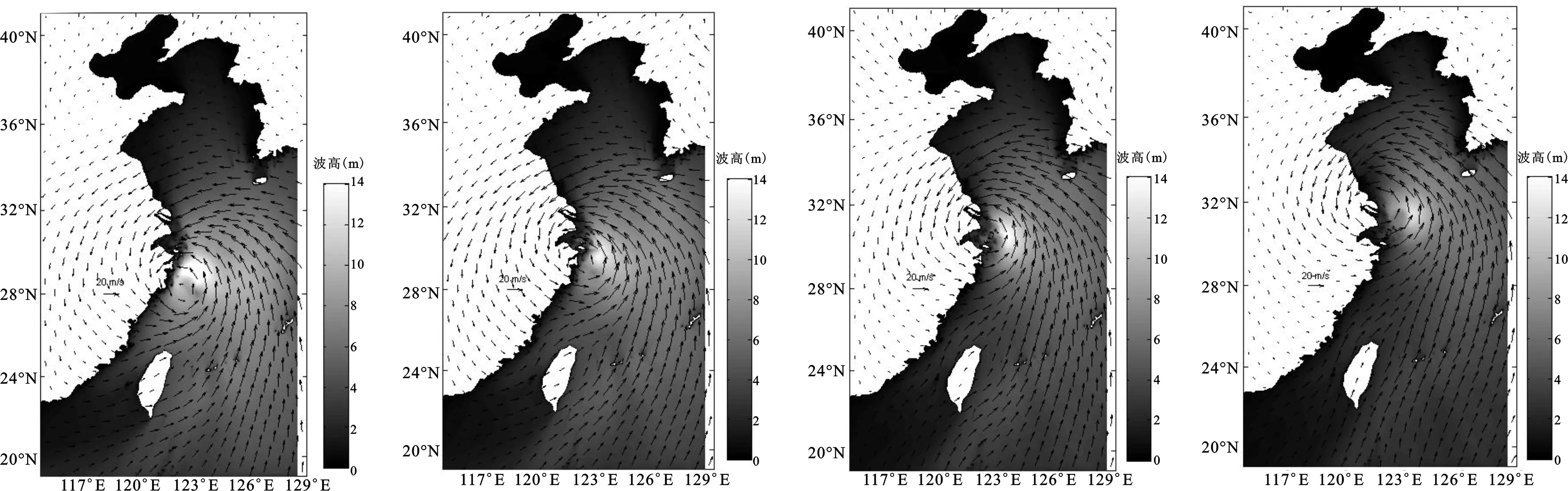
3-a7月11日8时3-b7月11日14时3-c7月11日20时3-d7月12日02时图3 大范围风场矢量和波高分布图Fig.3Distributionofwindspeedandwaveheightatlargecomputationarea

4 模型应用

SWAN是一种基于能量守恒原理的波浪谱模型，Holthuijsen等[9]对40.41版以后的SWAN模型进行改进，可更加全面地考虑地形变化影响下的波浪浅化、折射、反射、绕射、破碎、风能输入、波-波非线性相互作用和波浪耗散等效应，本模型采用40.91版SWAN。源汇项表示与波动能量的生成、消耗以及能量的再分布有关的物理过程，可由以下几部分组成

S=Sin+Snl3+Snl4+Sds,w+Sds,b+Sds,br

(10)

式中:Sin为风能量输入所致的波浪成长；Snl3为三波相互作用所导致的波浪能量非线性传播；Snl4为四波相互作用所致的波浪能量的非线性传输；Sds,w，Sds,b，Sds,br分别为白浪破碎所引起的波能衰减、底摩擦引起的波能衰减及水深变化导致的波浪破碎所引起的波能衰减。

4.1 工程区域模型的验证

规划区域建设用海工程的实施将改变岸线形态，导致规划区域及其附近海域波浪场变化，分别对南通近海的区域建设用海实施前、建设用海近期规划和远期规划实施后波浪场进行模拟研究，以分析区域建设用海对近岸波浪场的影响范围及程度。自嵌套小范围模拟区域采用非结构化网格，工程区域最小网格仅80 m。区域建设用海规划地形如图4所示，浅灰色表示南通近期区域建设用海工程规划，黑色为远期规划。波浪测站浮标验证数据有浮标处水深为8 m的响水测站(120.101°E，34.436°N)和蛎岈山波浪测站(121.568°E，32.147°N)，均为每小时采集一次数据，可以反映台风“灿鸿”期间台风成长全过程。用最适捷式合成风场作为SWAN自嵌套模型的驱动风场，模拟结果与波浪测站进行对比，如图5所示，实测数据与模拟值吻合度较高，该模型能很好地反映小范围海域内台风浪分布情况。

图4 南通近海区域建设用海规划及特征站位布置图Fig.4Tongzhoubayregionalconstructionschemeandstationarrangement5-a蛎岈山测站 5-b响水波浪测站图5 实测波浪测站有效波高与自嵌套小范围数值模拟值对比Fig.5Comparisonofthemeasuredsignificantwaveheightofwavestationwiththenestednumericalvaluesinasmallscope

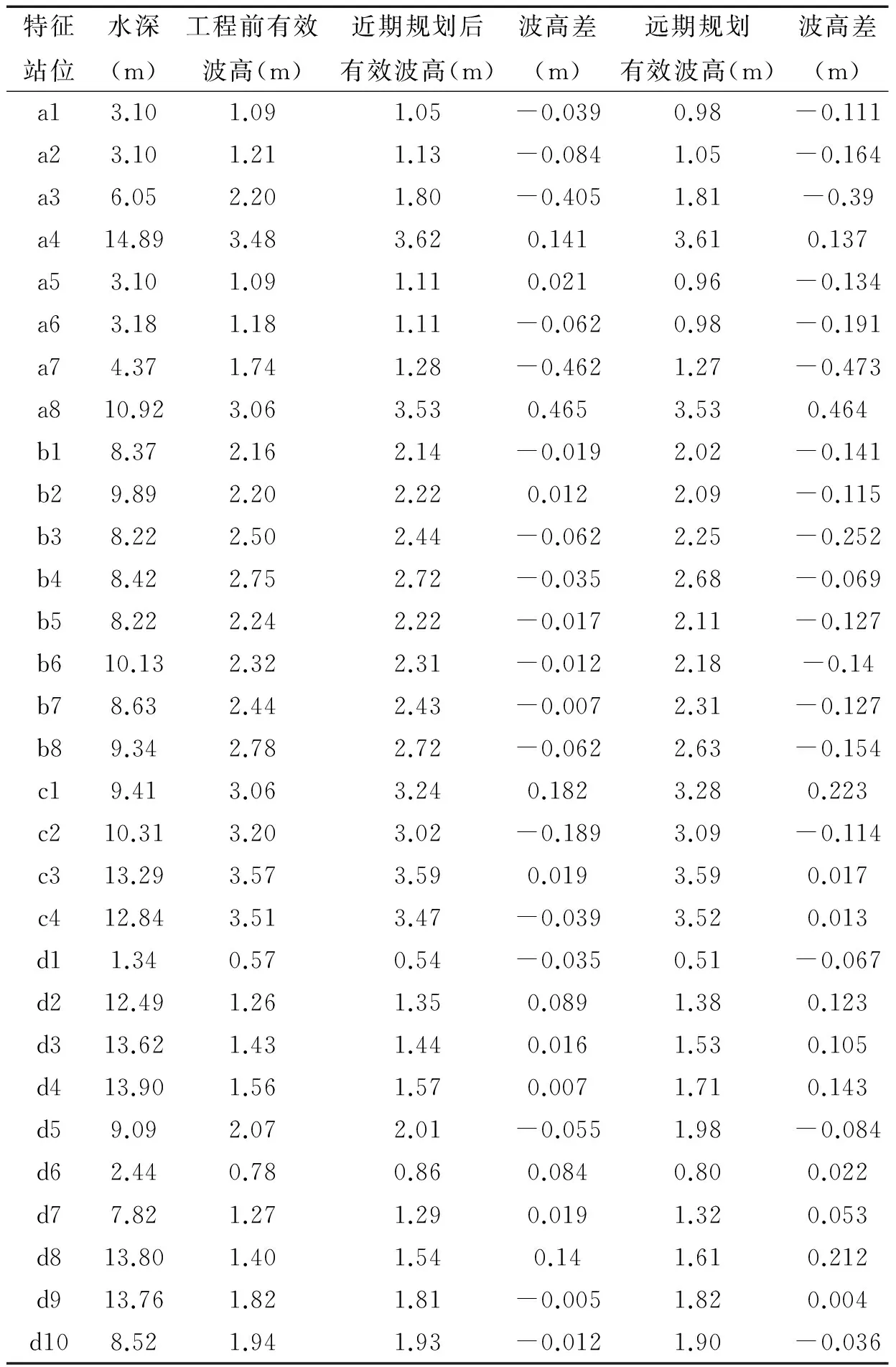
表3 特征站位水深，有效波高及波高变化Tab.3 Water depth,significant wave height and wave height variation in the station

4.2 工程对近海波浪场的影响

区域建设用海规划工程的实施将影响波高的时空分布变化，这种变化可能对近岸工程造成灾害性破坏，故对区域用海建设前后波高的变化进行研究不仅能有效减少潜在性灾害，还能提高区域用海工程建设布局规划的合理性，增加经济效益。篇幅所限，仅列举7月11号14时的波高分布图如图6所示，此时外海波向以ESE向为主。选取特征站位对其波高进行对比分析，如表3所示。

规划工程东部a、b区(a区即以字母a开头的特征站位及其附近海域，如特征站位a1～a8附近海域为a区，以此类推)所取特征站位平均水深7.5 m，近期用海规划工程实施较工程前波高以降低为主，其中a3、a7降幅达40 cm以上，而特征站位a8处波高明显增大，增幅达46.5 cm。这可能是由于工程的实施改变近岸水动力环境，造成波浪的原波峰线长度发生变化，在特征站位处辐聚、辐散，使其波高有增有减所致，a、b区所取特征站位平均降幅4 cm，其中a区降幅较b区更为明显。相对近期规划，远期用海规划工程实施后，平均波高降幅达12.4 cm，由于远期规划工程尤其是a、b区之间的建筑工程的实施，使其附近，尤其是b区波高明显降低，降幅大都在10 cm以上，其中特征站位b3比近期规划工程实施后波高减小19 cm。

c1～c4特征站位平均水深11.5 m，工程的实施改变其附近海域的波能分布，使其波高发生变化。近期规划实施后，所取特征站位平均有效波高降低不足1 cm，而c1、c3波高升降较为剧烈；在远期工程实施后平均波高增加了3.5 cm，其中离工程区域近的c1、c2特征站位较近期工程实施后，波高明显增大，可能是由于c区西部工程的实施，使其建筑物产生类似海岬岬角的效应所致。

南部航道d区所取特征站位平均水深9.7 m，近期规划工程的实施后d区附近海域波高以增加为主，特征站位d2、d6、d8处波高增幅约10 cm，较为显著，所取特征站位平均水深增加了2.5 cm。远期工程实施后，特征站位d2、d3、d4、d8增幅均在10 cm以上，其中d8增幅达20 cm以上，d3、d4特征站位较近期规划工程波高增幅更为明显，这可能是由于远期工程的实施使得反射作用更为显著所致。

相较规划工程实施前，近期区域用海规划工程实施后，全部特征站位平均有效波高降低4.5%，其中站位a3、a4、a6、a8、c1、c2附近海域波高变化剧烈，在其附近海域进行航海、渔业等海洋活动时，应考虑加强防护措施；远期区域用海规划工程实施后，平均波高降低了6.8%，但站位a8、c1、d8的有效波高增幅明显，若在其附近海域进行海洋工程建设，按工程原工况设计标准进行规划，可能带来越浪、溃堤等威胁，故需综合考虑，提高其附近海域海洋工程的设计标准。

6-a工程前6-b近期工程6-c远期工程图6 工程附近波高等值线分布图Fig.6Waveheightcontourmapinthevicinityofengineering

5 结论

在不同合成风场模式下对“灿鸿”进行台风浪数值模拟，采用卫星数据进行对比分析得出最适合成风场，并讨论南通近海规划工程对近海波浪场的影响：

(1)不同风场模型对比中，捷式合成风场模型的台风浪数值模拟效果最好，Holland次之，藤田最差。

(2)在最适风场模型下对南通近海规划进行应用分析：较近期规划，远期规划工程实施后，工程南部航道平均有效波高增幅更大；而东部区域平均波高降幅更明显。

(3)上述结论仅对北上型台风“灿鸿”适用，对其他台风的适用性还有待进一步研究。

[1]范从建,李瑞杰,戴路,等.江苏沿海滩涂围垦对近岸波浪场的影响[J].水运工程,2015 (12):16-22.

FAN C J, LI R J, DAI L, et al. Effects of tidal flat reclamation on wave′s field in Jiangsu coast[J]. Port and Waterway Engineering,2015(12):16-22.

[2]戴路,李瑞杰,梁连松,等.江苏沿海台风浪数值模拟[J].海洋环境科学,2016,36(6):838-845.

DAI L, LI R J, LIANG L S, et al. Numerical simulation of typhoon wave in Jiangsu coastal area[J]. Marine Environmental Science,2016,36(6)：838-845.

[3]梁连松,李瑞杰,丰青,等. 舟山海域台风浪数值模拟[J]. 水道港口,2014(6):582-588.

LIANG L S, LI R J, FENG Q, et al. Numerical simulation of typhoon wave in Zhoushan[J]. Journal of Waterway and Harbor,2014(6):582-588.

[4]杨支中,沙文钰,朱首贤,等. 一种新型的非对称台风的海面气压场和风场模型[J]. 海洋通报, 2005,24(1):1-7.

YANG Z Z, SHA W Y, ZHU S X, et al. A New Nonsymmetrical Model of the Sea Surface Pressure and Wind Fields about Typhoon[J]. Marine Science Bulletin, 2005,24(1)：1-7.

[5]唐建,史剑,李训强,等. 基于台风风场模型的台风浪数值模拟[J].海洋湖报,2013 (2):24-30.

TANG J, SHI J,LI X Q,et al. Numerical simulation of typhoon waves with typhoon wind mode[J]. Transactions of oceanology and Limnology，2013(2):24-30.

[6]Graham H E, Nunn D E. National Hurricane Research Project, Report No.33: Meteorological conditions pertinent to standard project hurricane Atlantic and Gulf Coasts of the United States[R]. US: US Department of Commerce and Weather Bureau, 1959.

[7]孔令双,戚定满,万远扬,等. 长江口海域波浪场模拟研究[J]. 水运工程, 2010(2):46-49.

KONG L S, QI D M, WAN Y Y, et al. Numerical simulation of wave field in the Yangtze Estuary[J]. Port and Waterway Engineering,2010(2):46-49.

[8]刘海成,刘海源,杨会利. 近岸波浪变形数值模型的比较研究[J].水道港口, 2009(3):153-158.

LIU H C, LIU H Y, YANG H L. Comparison of numerical models of nearshore wave transformation[J]. Journal of Waterway and Harbor, 2009(3):153-158.

[9]Holthuijsen L H, Herman A, Booij N. Phase-decoupled refraction-diffraction for spectral wave models[J]. Coastal Engineering, 2003, 49(4): 291-305.